Tick Bitmap Index

作为动态兑换的第一步，我们需要实现一个 tick 的索引。在之前的里程碑中，我们过去在进行兑换时计算目标 tick：

function swap(address recipient, bytes calldata data)
    public
    returns (int256 amount0, int256 amount1)
{
  int24 nextTick = 85184;
  ...
}

当在不同的价格范围内提供流动性时，我们不能简单地计算目标 tick。我们需要找到它。因此，我们需要索引所有具有流动性的 tick，然后使用该索引找到用于为兑换“注入”足够流动性的 tick。在这一步中，我们将实现这样一个索引。

Bitmap

Bitmap 是一种以紧凑方式索引数据的流行技术。Bitmap 仅仅是一个用二进制系统表示的数字，例如 31337 是 111101001101001。我们可以将其视为一个由零和一组成的数组，每个数字都有一个索引。然后我们说 0 表示未设置标志，1 表示已设置标志。因此，我们得到的是一个非常紧凑的索引标志数组：每个字节可以容纳 8 个标志。在 Solidity 中，我们可以有高达 256 位的整数，这意味着一个 uint256 可以容纳 256 个标志。

Uniswap V3 使用此技术来存储有关已初始化 tick 的信息，即具有一定流动性的 tick。当标志被设置 (1) 时，该 tick 具有流动性；当标志未被设置 (0) 时，该 tick 未被初始化。让我们看一下实现。

TickBitmap 合约

在池合约中，tick 索引存储在一个状态变量中：

contract UniswapV3Pool {
    using TickBitmap for mapping(int16 => uint256);
    mapping(int16 => uint256) public tickBitmap;
    ...
}

这是一个映射，其中键是 int16，值是 words (uint256)。想象一个由 1 和 0 组成的无限连续数组：

此数组中的每个元素对应于一个 tick。要在此数组中导航，我们将其分解为 words：长度为 256 位的子数组。要找到 tick 在此数组中的位置，我们执行以下操作：

function position(int24 tick) private pure returns (int16 wordPos, uint8 bitPos) {
    wordPos = int16(tick >> 8);
    bitPos = uint8(uint24(tick % 256));
}

也就是说：我们找到它的 word 位置，然后找到它在该 word 中的位。>> 8 等同于整数除以 256。因此，word 位置是 tick 索引除以 256 的整数部分，而位位置是余数。

作为一个例子，让我们计算一个我们的 tick 的 word 和位位置：

tick = 85176
word_pos = tick >> 8 # or tick // 2**8
bit_pos = tick % 256
print(f"Word {word_pos}, bit {bit_pos}")
# Word 332, bit 184

翻转 Flags

当将流动性添加到池中时，我们需要在 bitmap 中设置一些 tick 标志：一个用于较低的 tick，一个用于较高的 tick。我们在 bitmap mapping 的 flipTick 方法中执行此操作：

function flipTick(
    mapping(int16 => uint256) storage self,
    int24 tick,
    int24 tickSpacing
) internal {
    require(tick % tickSpacing == 0); // 确保 tick 是间隔的
    (int16 wordPos, uint8 bitPos) = position(tick / tickSpacing);
    uint256 mask = 1 << bitPos;
    self[wordPos] ^= mask;
}

在本书的后面部分，tickSpacing 始终为 1。请记住，此值会影响可以初始化的 tick：当它等于 1 时，可以翻转所有 tick；当它设置为不同的值时，只能翻转可以被该值整除的 tick。

在找到 word 和位位置后，我们需要创建一个 mask。mask 是一个数字，该数字在 tick 的位位置处设置了一个 1 标志。要找到 mask，我们只需计算 2**bit_pos（等效于 1 << bit_pos）：

mask = 2**bit_pos # or 1 << bit_pos
print(format(mask, '#0258b'))                                             ↓ 这里
#0b00000000000000000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

接下来，要翻转一个标志，我们通过按位异或将 mask 应用于 tick 的 word：

word = (2**256) - 1 # 将 word 设置为全 1
print(format(word ^ mask, '#0258b'))                                      ↓ 这里
#0b1111111111111111111111111111111111111111111111111111111111111111111111101111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111

您会看到第 184 位（从右侧开始计数，从 0 开始）已翻转为 0。

如果一个位为零，它会将其设置为 1：

word = 0
print(format(word ^ mask, '#0258b'))                                      ↓ 这里
#0b000000000000000000000000000000000000000000000000000000000000000000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

查找下一个 Tick

下一步是使用 bitmap 索引查找具有流动性的 tick。

在兑换期间，我们需要找到一个具有流动性的 tick，该 tick 位于当前 tick 之前或之后（即：位于其左侧或右侧）。在之前的里程碑中，我们过去计算并硬编码它，但现在我们需要使用 bitmap 索引找到这样的 tick。我们将在 TickBitmap.nextInitializedTickWithinOneWord 函数中执行此操作。在此函数中，我们需要实现两种情况：

1. 当出售 token $x$（在我们的例子中为 ETH）时，在当前 tick 的 word 中并且在当前 tick 的右侧 找到下一个初始化的 tick。
2. 当出售 token $y$（在我们的例子中为 USDC）时，在下一个（当前 + 1）tick 的 word 中并且在当前 tick 的左侧 找到下一个初始化的 tick。

这对应于在任一方向进行兑换时的价格变动：

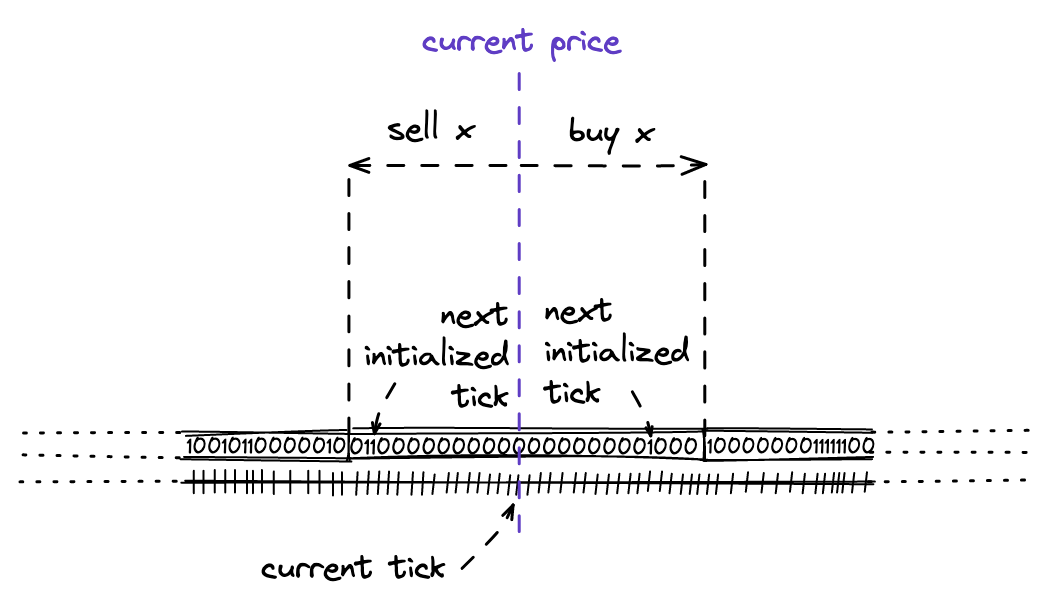
请注意，在代码中，方向已翻转：当购买 token $x$ 时，我们搜索当前左侧的已初始化 tick；当出售 token $x$ 时，我们搜索右侧的 tick。但这仅在 word 中成立；word 从左到右排序。

当当前 word 中没有初始化的 tick 时，我们将在下一个循环周期中继续在相邻的 word 中搜索。

现在，让我们看一下实现：

function nextInitializedTickWithinOneWord(
    mapping(int16 => uint256) storage self,
    int24 tick,
    int24 tickSpacing,
    bool lte
) internal view returns (int24 next, bool initialized) {
    int24 compressed = tick / tickSpacing;
    ...

1. 第一个参数使此函数成为 mapping(int16 => uint256) 的方法。
2. tick 是当前 tick。
3. 在我们在里程碑 4 中开始使用它之前，tickSpacing 始终为 1。
4. lte 是设置方向的标志。当 true 时，我们正在出售 token $x$ 并搜索当前 tick 右侧的下一个已初始化 tick。当 false 时，情况正好相反。lte 等于兑换方向：出售 token $x$ 时为 true，否则为 false。

if (lte) {
    (int16 wordPos, uint8 bitPos) = position(compressed);
    uint256 mask = (1 << bitPos) - 1 + (1 << bitPos);
    uint256 masked = self[wordPos] & mask;
    ...

当出售 $x$ 时，我们正在：

1. 获取当前 tick 的 word 和位位置；
2. 创建一个 mask，其中当前位位置（包括它）右侧的所有位都为 1（mask 全为 1，其长度 = bitPos）；
3. 将 mask 应用于当前 tick 的 word。

    ...
    initialized = masked != 0;
    next = initialized
        ? (compressed - int24(uint24(bitPos - BitMath.mostSignificantBit(masked)))) * tickSpacing
        : (compressed - int24(uint24(bitPos))) * tickSpacing;
    ...

接下来，如果其至少一位设置为 1，则 masked 将不等于 0。如果是这样，则存在已初始化的 tick；如果不是，则不存在（不在当前 word 中）。根据结果​​，我们要么返回下一个已初始化 tick 的索引，要么返回下一个 word 中最左边的位——这将使我们可以在另一个循环周期中搜索词中的已初始化 tick。

    ...
} else {
    (int16 wordPos, uint8 bitPos) = position(compressed + 1);
    uint256 mask = ~((1 << bitPos) - 1);
    uint256 masked = self[wordPos] & mask;
    ...

同样，当出售 $y$ 时，我们：

1. 获取当前 tick 的 word 和位位置；
2. 创建一个不同的 mask，其中当前 tick 位位置左侧的所有位都为 1，而右侧的所有位都为零；
3. 将 mask 应用于当前 tick 的 word。

同样，如果没有已初始化 tick 在左侧，则返回上一个 word 的最右边的位：

    ...
    initialized = masked != 0;
    // overflow/underflow is possible, but prevented externally by limiting both tickSpacing and tick
    next = initialized
        ? (compressed + 1 + int24(uint24((BitMath.leastSignificantBit(masked) - bitPos)))) * tickSpacing
        : (compressed + 1 + int24(uint24((type(uint8).max - bitPos)))) * tickSpacing;
}

就是这样！

如你所见，如果 nextInitializedTickWithinOneWord 离得很远，则找不到确切的 tick——它的搜索范围是当前或下一个 tick 的 word。 实际上，我们不想迭代无限的 bitmap 索引。