Uniswap V3 简介

本章节复述了 Uniswap V3 的白皮书。同样，如果你不理解所有概念也没关系。当它们转化为代码时会更清晰。

为了更好地理解 Uniswap V3 带来的创新，让我们首先看看 Uniswap V2 的不足之处。

Uniswap V2 是一个通用的交易所，它实现了一种 AMM 算法。然而，并非所有的交易对都是一样的。交易对可以按价格波动性分组：

1. 具有中高价格波动性的 Token。这个组包括大多数 Token，因为大多数 Token 的价格没有与任何事物挂钩，并且会受到市场波动的影响。
2. 具有低波动性的 Token。这个组包括挂钩 Token，主要是稳定币：USDC/USDT、USDC/DAI、USDT/DAI 等。还有：ETH/stETH、ETH/rETH (wrapped ETH 的变体)。

这些组需要不同的，我们称之为，池配置。主要的区别在于，挂钩 Token 需要高流动性来减少大额交易的需求效应（我们在上一章中已经了解过）。USDC 和 USDT 的价格必须保持接近 1，无论我们想要买卖的 Token 数量有多大。由于 Uniswap V2 的通用 AMM 算法不太适合稳定币交易，因此替代的 AMM（主要是 Curve）在稳定币交易中更受欢迎。

造成这个问题的原因是 Uniswap V2 池中的流动性是无限分布的——池流动性允许在任何价格下进行交易，从 0 到无穷大：

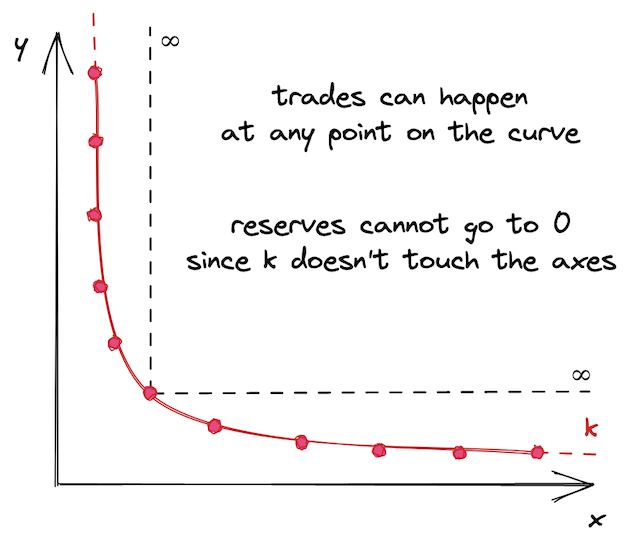
这可能看起来不是一件坏事，但这使得资本效率低下。资产的历史价格保持在某个定义的范围内，无论是窄范围还是宽范围。例如，ETH 的历史价格范围是从 0.75 美元到 4,800 美元（根据 CoinMarketCap）。今天（2022 年 6 月，1 个 ETH 的价格为 1,800 美元），没有人会以 5000 美元的价格购买 1 个以太币，因此在这个价格提供流动性是没有意义的。因此，在远离当前价格或永远无法达到的价格范围内提供流动性是没有意义的。

然而，我们都相信 ETH 总有一天会达到 10,000 美元。

集中流动性

Uniswap V3 引入了 集中流动性：流动性提供者现在可以选择他们想要提供流动性的价格范围。这通过允许将更多流动性投入到狭窄的价格范围内来提高资本效率，这使得 Uniswap 更加多样化：它现在可以拥有为具有不同波动性的交易对配置的池子。这就是 V3 改进 V2 的方式。

简而言之，一个 Uniswap V3 交易对是许多小的 Uniswap V2 交易对。V2 和 V3 之间的主要区别在于，在 V3 中，一个交易对中存在许多价格范围。并且每个较短的价格范围都有有限的储备。从 0 到无穷大的整个价格范围被分成较短的价格范围，每个价格范围都有自己的流动性数量。但是，至关重要的是，在该较短的价格范围内，它的工作方式与 Uniswap V2 完全相同。这就是为什么我说一个 V3 交易对是许多小的 V2 交易对。

现在，让我们尝试将其可视化。我们想说的是，我们不希望曲线是无限的。我们在 $a$ 和 $b$ 点将其截断，并说这些是曲线的边界。此外，我们移动曲线，使边界位于轴上。这就是我们得到的：

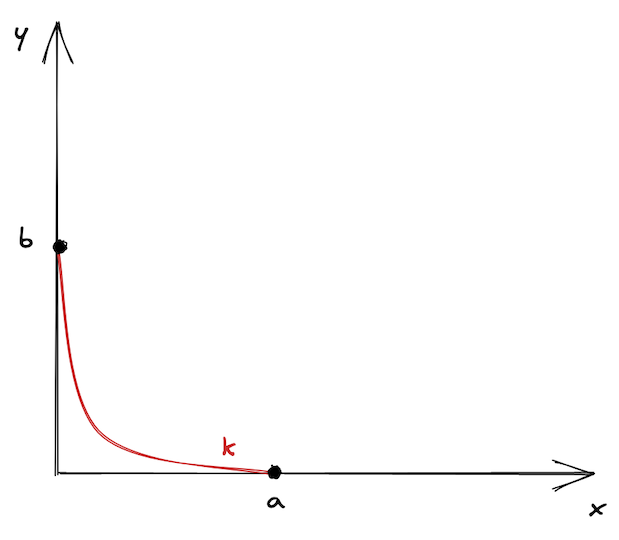
它看起来很孤单，不是吗？这就是为什么 Uniswap V3 中存在许多价格范围——这样它们就不会感到孤单🙂

正如我们在上一章中看到的那样，买卖 Token 会使价格沿着曲线移动。价格范围限制了价格的移动。当价格移动到任一端点时，池会变得耗尽：其中一个 Token 储备将为 0，并且购买该 Token 将不可能。

在上图中，假设起始价格位于曲线的中间。要到达 $a$ 点，我们需要购买所有可用的 $y$ 并在范围内最大化 $x$；要到达 $b$ 点，我们需要购买所有可用的 $x$ 并在范围内最大化 $y$。在这些点上，范围内只有一种 Token！

有趣的事实：这允许使用 Uniswap V3 价格范围作为限价单！

当当前价格范围在交易期间耗尽时会发生什么？价格会滑入下一个价格范围。如果下一个价格范围不存在，则交易最终会部分完成——我们将在本书的后面部分看到它是如何工作的。

这是流动性在 生产中的 USDC/ETH 池 中分布的方式：

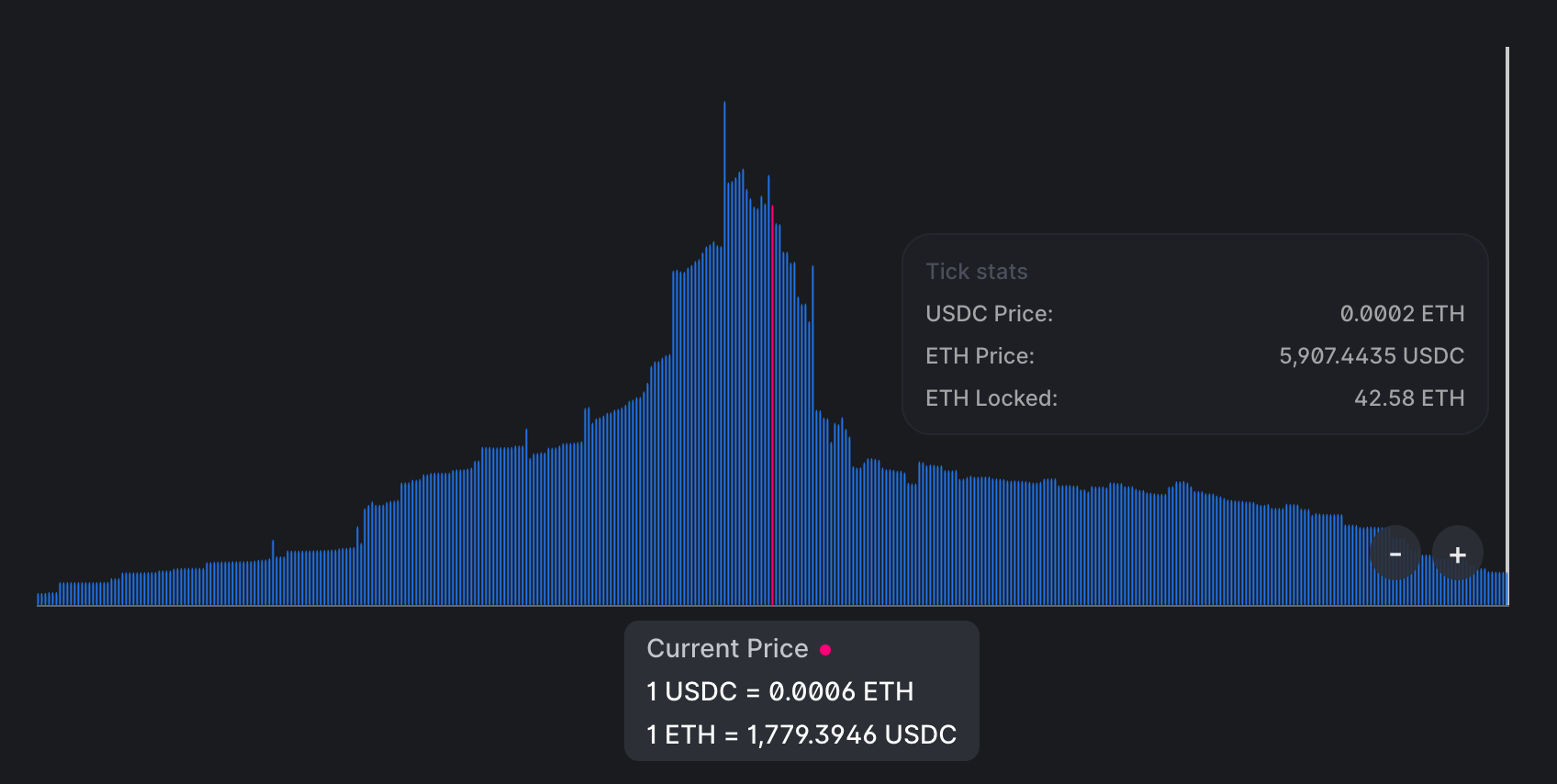
你可以看到，当前价格附近有很多流动性，但离它越远，流动性就越少——这是因为流动性提供者努力提高其资本的效率。此外，整个范围不是无限的，其上限显示在图像中。

Uniswap V3 的数学原理

从数学上讲，Uniswap V3 基于 V2：它使用相同的公式，但它们是……我们称之为增强。

为了处理价格范围之间的转换，简化流动性管理并避免舍入误差，Uniswap V3 使用了以下新概念：

$$L = \sqrt{xy}$$

$$\sqrt{P} = \sqrt{\frac{y}{x}}$$

$L$ 是流动性数量。池中的流动性是 Token 储备的组合（即，两个数字）。我们知道它们的乘积是 $k$，我们可以使用它来推导出流动性的度量，即 $\sqrt{xy}$——一个数字，当它自身相乘时，等于 $k$。$L$ 是 $x$ 和 $y$ 的几何平均值。

$y/x$ 是以 1 为单位的 Token 0 的价格。由于池中 Token 的价格互为倒数，因此我们可以在计算中仅使用其中一个（按照惯例，Uniswap V3 使用 $y/x$）。以 Token 0 为单位的 Token 1 的价格很简单 $\frac{1}{y/x}=\frac{x}{y}$。类似地，$\frac{1}{\sqrt{P}} = \frac{1}{\sqrt{y/x}} = \sqrt{\frac{x}{y}}$。

为什么使用 $\sqrt{p}$ 而不是 $p$？有两个原因：

1. 平方根计算不精确，会导致舍入误差。因此，更容易存储平方根而无需在合约中计算它（我们不会在合约中存储 $x$ 和 $y$）。

2. $\sqrt{P}$ 与 $L$ 有一个有趣的联系：$L$ 也是输出量变化与 $\sqrt{P}$ 变化之间的关系。

   $$L = \frac{\Delta y}{\Delta\sqrt{P}}$$

证明: $$L = \frac{\Delta y}{\Delta\sqrt{P}}$$ $$\sqrt{xy} = \frac{y_1 - y_0}{\sqrt{P_1} - \sqrt{P_0}}$$ $$\sqrt{xy} (\sqrt{P_1} - \sqrt{P_0}) = y_1 - y_0$$ $$\sqrt{xy} (\sqrt{\frac{y_1}{x_1}} - \sqrt{\frac{y_0}{x_0}}) = y_1 - y_0$$ $$\textrm{Since } \sqrt{x_1y_1} = \sqrt{x_0y_0} = \sqrt{xy} = L,$$ $$\sqrt{\frac{x_1y_1y_1}{x_1}} - \sqrt{\frac{x_0y_0y_0}{x_0}} = y_1 - y_0$$ $$\sqrt{y_1^2} - \sqrt{y_0^2} = y_1 - y_0$$ $$y_1 - y_0 = y_1 - y_0$$

定价

同样，我们不需要计算实际的价格——我们可以立即计算出输出数量。此外，由于我们不会跟踪和存储 $x$ 和 $y$，因此我们的计算将仅基于 $L$ 和 $\sqrt{P}$。

从上面的公式中，我们可以找到 $\Delta y$:

$$\Delta y = \Delta \sqrt{P} L$$

参见上面证明中的第三步。

正如我们上面讨论的那样，池中的价格互为倒数。因此，$\Delta x$ 是：

$$\Delta x = \Delta \frac{1}{\sqrt{P}} L$$

$L$ 和 $\sqrt{P}$ 允许我们不存储和更新池储备。此外，我们不需要每次都计算 $\sqrt{P}$，因为我们总是可以找到 $\Delta \sqrt{P}$ 及其倒数。

Ticks (价格跳动)

正如我们在本章中所了解的那样，V2 的无限价格范围在 V3 中被分成较短的价格范围。每个较短的价格范围都受到边界的限制——上限和下限。为了跟踪这些边界的坐标，Uniswap V3 使用 ticks（价格跳动）。

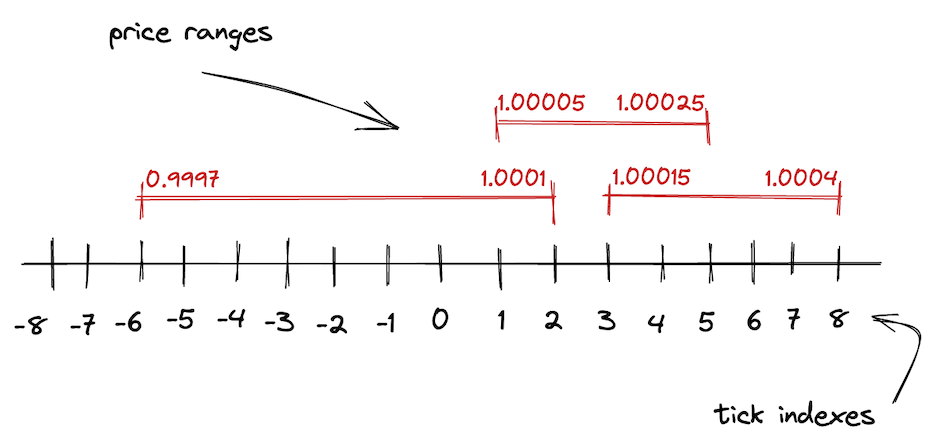
在 V3 中，整个价格范围由均匀分布的离散价格跳动来划分。每个价格跳动都有一个索引，对应于某个价格：

$$p(i) = 1.0001^i$$

其中 $p(i)$ 是价格跳动 $i$ 处的价格。取 1.0001 的幂具有一个理想的属性：两个相邻的价格跳动之间的差为 0.01% 或 1 个基点。

基点（1/100 的 1%，或 0.01%，或 0.0001）是金融中百分比的度量单位。当中央银行宣布利率变化时，你可能听说过基点。

正如我们上面讨论的那样，Uniswap V3 存储 $\sqrt{P}$，而不是 $P$。因此，公式实际上是：

$$\sqrt{p(i)} = \sqrt{1.0001}^i = 1.0001 ^{\frac{i}{2}}$$

因此，我们得到这样的值：$\sqrt{p(0)} = 1$，$\sqrt{p(1)} = \sqrt{1.0001} \approx 1.00005$，$\sqrt{p(-1)} \approx 0.99995$。

价格跳动是整数，可以是正数和负数，当然，它们不是无限的。Uniswap V3 将 $\sqrt{P}$ 存储为定点 Q64.96 数字，这是一个有理数，使用 64 位表示整数部分，使用 96 位表示小数部分。因此，价格（等于 $\sqrt{P}$ 的平方）在以下范围内：$[2^{-128}, 2^{128}]$。价格跳动在以下范围内：

$$[log{1.0001}2^{-128}, log{1.0001}{2^{128}}] = [-887272, 887272]$$

为了更深入地了解 Uniswap V3 的数学原理，我不得不推荐 Atis Elsts 的 这篇技术说明。