当大多数人听到零知识证明（ZKP）时，他们会想到加密钱包和区块链 Rollup但是，ZKPs 正在悄然驱动一类新的隐私优先应用程序——从人工智能到云基础设施——远在 Web3 之外

当大多数人听到零知识证明 (ZKPs) 时，他们会想到加密钱包和区块链 Rollup。但 ZKP 正在悄悄地为一类新的以隐私为先的应用提供动力——从人工智能到云基础设施——远远超出了 Web3 的范畴。

从本质上讲，ZKP 允许一方证明一个陈述是真实的，而不揭示它为什么是真实的。这听起来很抽象——但在实践中，这意味着你可以证明你的年龄而无需出示你的身份证，证明一个机器学习的结果而无需透露输入，或者验证远程服务器的安全性，而无需信任运行它的公司。

在本文中，我们将探讨 ZKP 如何被大型公司在现实世界的系统中使用，例如：

• Google 在 Wallet 中使用 ZKP 来验证年龄和身份，而不会泄露个人详细信息
• Cloudflare 利用 ZKP 进行私有 Web 认证，证明浏览器的状态而不会泄露用户数据
• EZKL，一个用于保护隐私的机器学习的开源 zkML 工具包
• TikTok 的隐私创新团队，他们正在使用 ZKP 为 TEE 构建一个无需信任的远程认证系统

每个项目都展示了零知识可以做到的不同方面——不仅仅是作为一种金融匿名工具，而是作为一种更私密、可验证和尊重用户的互联网的基本构建块。

Google：来自 ECDSA 的匿名凭证

证明敏感属性（如“年龄≥18”）可能是一个隐私雷区。传统方法受以下因素影响：

• 数据泄露： 上传驾照照片会将你的完整身份暴露给任何服务器泄露。
• 通过认证密钥进行跟踪： MDOC 风格的移动 ID 依赖于硬件密钥来实现防重放，但这些相同的密钥可用于跨站点对你进行指纹识别和跟踪。
• 遗留硬件和兼容性： 许多较旧的手机和安全密钥不支持没有固件更新的现代匿名凭证方案（例如 Idemix、CL 签名）——使用户陷入不安全的方法或被完全排除在外。

Google 的“来自 ECDSA 的匿名凭证”解决了上述所有问题：它使用无处不在的 ECDSA 硬件接口来实现广泛的兼容性，但提供了真正的匿名性和零知识。

核心思想扩展

当你要求 Google Wallet 证明一个属性（例如，“年龄≥18”）时，它实际上会构建一个复杂的语句，然后在该语句上运行两层零知识证明（sumcheck + Ligero）。以下是它的分解方式：

1. MDOC 脚本组件

MDOC（移动驾驶执照）证明生成一个包含以下内容的脚本：

• 签名 1 (sig_1)：由颁发机构（例如 DMV）对凭证数据的哈希值进行的 ECDSA 签名。

• 公共属性原像：MDL 中的一个字段，例如

   MDL["valueDigests"]["org.iso.18013.5.1"]["age_over_18"] = True

  与随机 nonce 一起，将其哈希以产生 $h2=SHA256(nonce∥"age_over_18"∥"True")$， $$ h_2 = \mathrm{SHA256}(\mathrm{nonce} \,|\, \text{"age_over_18"} \,|\, \text{"True"})\,, $$ 证明该属性而不泄露出生日期本身。

• 签名 2 (sig_2)：设备硬件密钥对服务器质询脚本的 ECDSA 签名，以防止重放。

• 有效期范围：两个时间戳 time_start 和 time_end，检查确保

  time_start < time_now < time_end

  2. Sumcheck 证明者
• 钱包运行交互式 sumcheck 协议，以让（虚拟）验证者相信确实通过了两个 ECDSA 验证、SHA-256 原像检查和时间戳范围检查。
  3. 非交互式 Ligero 包装
• 在 sumcheck 之后，钱包运行 Ligero 证明者以生成零知识证明，证明 sumcheck 脚本将被 sumcheck 验证者接受。
• 生成的证明是 简洁的，并且 仅 揭示所有检查都已通过，而不暴露 sig_1、sig_2、nonce 或任何其他内部数据。

通过将 sumcheck 与 Ligero 组合（一种借用自最新 ZK 研究的技术），Google Wallet 在证明你的属性（例如“年龄≥18”）有效时，提供硬件级别的安全性、新鲜度和真正的匿名性——而无需泄露你的 ID、设备密钥或生物识别数据。

Cloudflare — 使用零知识证明的私有 Web 认证

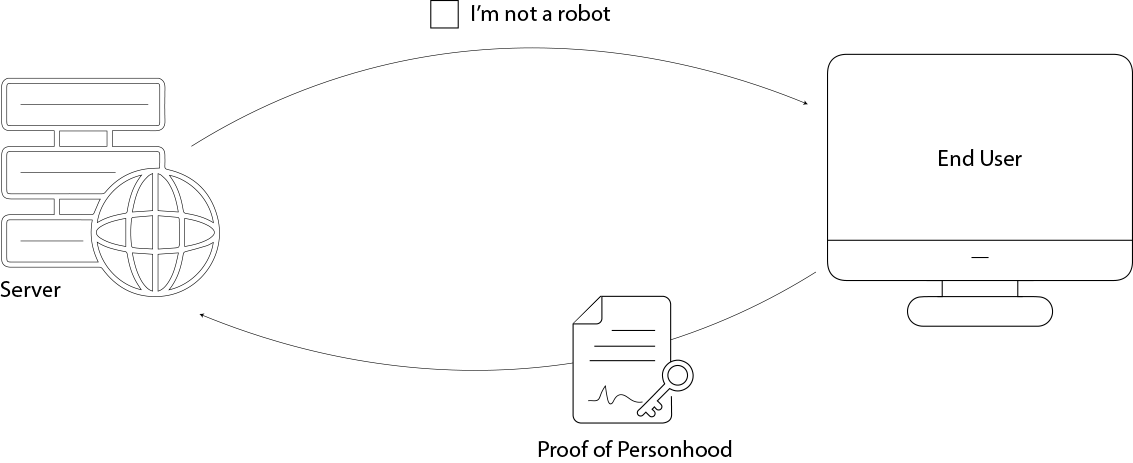
Cloudflare 正在重新构想我们如何在互联网上证明我们是真人——不是通过 CAPTCHA 难题或用户帐户，而是通过尊重隐私的硬件支持的证明。

传统上，网站使用 WebAuthn 认证来验证用户的硬件密钥（如 YubiKey）。此认证使用数字签名和证书链证明密钥是真实的并且由受信任的制造商颁发。但存在一个隐私问题：认证会泄露元数据——如密钥的制造商和型号——这些元数据可以与其他浏览器信号组合起来以帮助对用户进行指纹识别。

即使 WebAuthn 在设计时考虑了隐私政策，Cloudflare 也希望更进一步。他们的目标：验证用户是否持有受信任的硬件密钥——而不了解有关它的任何其他信息。

他们真正需要的只是一个二元答案：“这是一个真实的、未被破坏的安全密钥吗？” 他们不关心谁制造的、什么型号的，或者存在多少个与它类似的东西。

进入零知识证明

Cloudflare 设计了一个自定义的 零知识证明 (ZKP) 协议 来做到这一点。

浏览器不是发送原始认证签名（这会泄露元数据），而是构造一个 ZKP，该 ZKP 证明：

• 签名是由来自受信任列表的密钥生成的（例如，通过 FIDO 认证），并且
• 签名对于服务器发送的消息有效

所有这些都在不泄露它是哪个密钥的情况下得到证明。服务器只知道：“是的，一个有效的、值得信赖的密钥签署了这个。”

如何运作

生成 Tom 曲线的动机

在该协议中，我们需要在零知识证明中将椭圆曲线运算表示为算术约束。诸如 P-256 之类的标准曲线是在其群阶 $r$ 与 $p$ 不同 的素数域 $F_p$ 上定义的。这种不匹配会产生一个主要问题： 群运算（点加法、标量乘法）以群阶 $r$ 为模进行。域运算（坐标的加/乘）以素数 $p$ 为模进行。

在 ZK 电路中，混合两个模意味着为 $r$ 和 $p$ 的模约简构建单独的约束小工具，从而大致使复杂性加倍。

为了避免这种情况，该团队着手设计新的曲线（昵称为 Tom 曲线），以便新曲线的群阶与原始曲线的基域大小相匹配。这使得所有算术运算都在同一域 $F_p$ 中进行

在实践中，生成 Tom 曲线意味着：

1. 从 ECDSA 域开始

令 $p$ 为现有 ECDSA 曲线（例如 P-256 的字段素数）的素数模数。其群阶是另一个素数 $r$。

2. 在 $F_q$ 上搜索阶数为 $p$ 的曲线

找到系数 $a,b$ 使得曲线

$E': y^2 = x^3 + a x + b \quad\text{在 }F_q\text{ 上}$

满足

$#E'(F_q) = p.$

通过颠倒通常的设计——首先固定阶数，然后找到曲线——该团队解锁了一种效率更高、对 ZK 友好的椭圆曲线，该曲线支持 zkAttest 的高性能证明。

高级工作流程

1. 环设置

受信任的认证公钥的公共环

$R = {\,pk_1, pk_2, \dots, pk_n\,}$

代表由 FIDO（快速身份在线）认证的所有硬件密钥。

2. 提交你的密钥 证明者持有 $(sk, pk)$，其中 $pk \in R$。他们采样随机性 $r$ 并计算 Pedersen 承诺（使用群生成器 $G, H$）： $C_{pk} = pkG + rH$
3. 生成签名 使用 ECDSA，设备对服务器的质询 $m$ 进行签名，得到 $\sigma = (r, s)$。
4. 生成 ZK 证明 $\pi$

证明者构造一个非交互式证明 $\pi$，该证明由两个子证明组成：

• 签名有效性 ($\pi_{\text{sig}}$)：证明 $(sk,r,s)$ 的知识，使得 $\sigma$ 是在已提交的 $pk$ 下的正确的 ECDSA 签名。
• 环成员资格 ($\pi_{\text{mem}}$)：证明已提交的 $pk$ 属于 $R$。
  5. 提交给验证者

发送 $(C_{pk},\,\sigma,\,\pi)$。验证者检查：

• $C{pk}$ 的 Pedersen 开放与$\pi{\text{sig}}$ 和 $\pi_{\text{mem}}$ 一致。

• $\pi_{\text{sig}}$ 验证已提交的密钥下的 $\sigma$。

• $\pi_{\text{mem}}$ 验证 $pk\in R$。

证明 1：签名有效性 ($\pi_{\text{sig}}$)

我们需要证明设备的 ECDSA 签名有效，而不 泄露其密钥。为此：

1. 备用 ECDSA 检查

重写通常的验证 $u_1=H(m)s^{-1},\;u_2=r\,s^{-1},\;R=u_1G+u_2Q,\;r\stackrel{?}{=}R_x$ 作为单一关系

$zR - H(m)r^{-1}G = Q,\quad z=s\,r^{-1}.$

2. 提交并证明

   • 提交到公钥 $Q$ 和标量 $z$：

     $C_Q=\mathsf{Com}(Q),\quad C_z=\mathsf{Com}(z).$

   • 提交到 $S=H(m)r^{-1}G$ 和 $P=zR$:

     $C_S=\mathsf{Com}(S),\quad C_P=\mathsf{Com}(P).$

   • 使用标量乘小工具证明 $P=zR$ 和一个点加小工具证明

     $P - S = Q$

     在已提交的值上。

此零知识证明确认签名是真实的，而不会暴露 $sk$ 或 $z$。

证明 2：环成员资格 ($\pi_{\text{mem}}$)

为了证明已提交的公钥 $Q$ 是“受信任的密钥”之一，而不泄露是哪一个，zkAttest 利用 Pedersen 承诺的 多选一 ZK 证明。本质上：

1. 提交所有密钥

可以获得每个 $pk_j$ 的承诺的公共列表，以及证明者自己对 $Q$ 的承诺。

2. 应用多选一小工具

证明者对这些承诺运行标准的多选一零知识协议，以显示 “我知道完全一个与我的承诺匹配的承诺的开放。”

3. 零知识成员资格

此非交互式证明使验证者确信 $Q$ 属于已发布的密钥集，同时对匹配索引完全隐藏。

通过使用经典的多选一证明系统，zkAttest 实现了私有、高效的集合成员资格，而不会暴露任何额外信息。

结合在一起

最终证明 $\pi$ 是 $\pi{\text{sig}}$ 和 $\pi{\text{mem}}$ 的串联，通过 Fiat-Shamir 实现非交互性。借助 zkAttest，Cloudflare 实现了 无需信任的、保护隐私的认证：服务器 仅 知道“这是一个真实的、未被破坏的安全密钥”——仅此而已。

EZKL — 使用 ZKP 的可证明机器学习

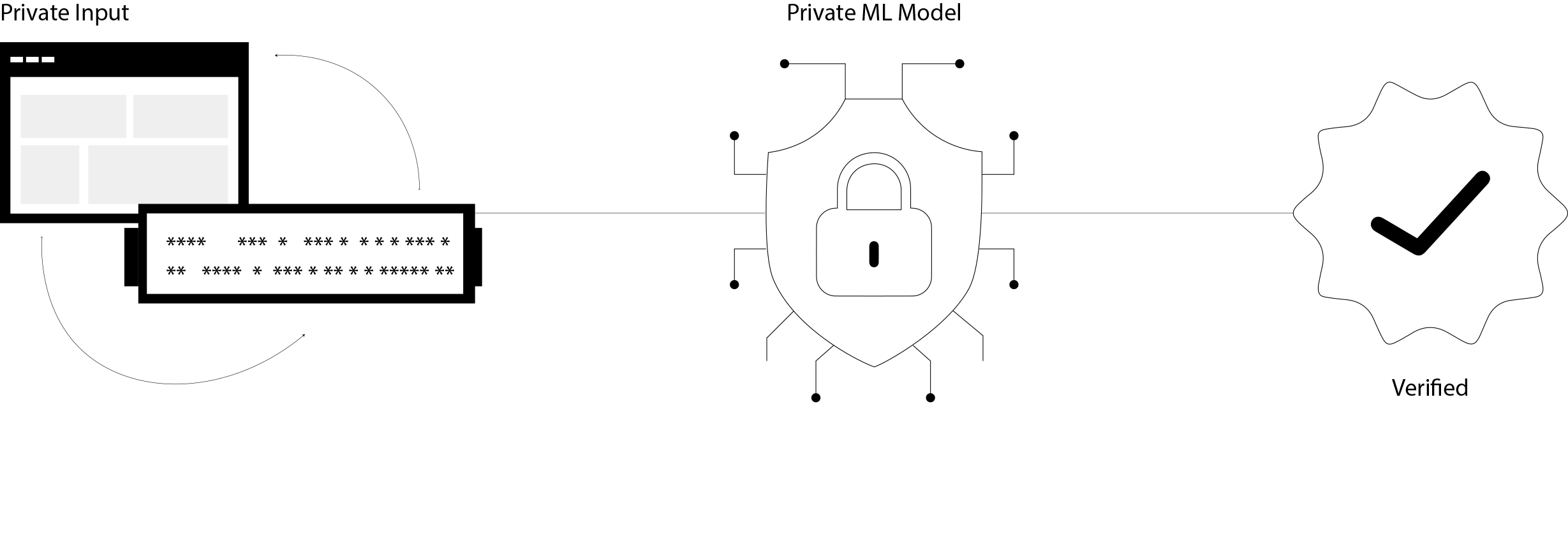
在许多场景中，我们需要说服某人神经网络推理已正确执行——但不会暴露敏感细节。例如，你可能想要证明：

1. 你在 公共数据 上运行了 私有模型，
2. 你在 私有数据 上运行了 公共模型，或者
3. 你在 公共数据 上运行了 公共模型。

每个组合都解决了不同的隐私与可验证性之间的权衡，但它们都具有相同的核心目标：“我执行了一个神经网络，并在权重 $W$ 下从输入 $x$ 生成了输出 $y$”，而不会泄露秘密。

实现这一点需要克服几个技术障碍：

• 场化浮点运算

真实世界的神经网络依赖于矩阵乘法、非线性激活（例如 ReLU）和其他浮点例程。为了在 ZK 中证明它们的正确性，我们必须将它们表示为素数域 $F_p$ 中的精确算术。

• 可扩展的证明

现代模型可以有数百万个参数。证明生成和验证必须以门数为单位 亚线性 增长，否则它们将变得不切实际。

• 灵活的保密

根据用例，模型权重 $W$、输入 $x$ 或两者可能都需要保持私有。证明系统必须无缝地处理每个组件上的 公共/秘密 标志。

在下一节中，我们将了解 EZKL 的编译器、优化器和基于 Halo2 的证明后端如何协同工作来解决这些挑战。

架构概述

EZKL 的设计将 zkML 管道分为四个清晰的阶段，每个阶段都处理将神经网络转换为简洁的零知识证明的关键方面。

1. 模型编译器
   • 它做什么： 解析通用格式（例如 PyTorch）并将每一层（矩阵乘法、Rollup、激活）转换为素数域 $F_p$ 上的算术门。
   • 为什么它很重要： 提供神经网络的真实、基于域的表示，为证明生成奠定基础。
2. 电路优化器
   • 它做什么： 应用一系列优化：
   • 用于输入和中间值的 范围检查，确保它们适合预期的位宽。
   • 激活近似（例如，用对域友好的函数近似 ReLU）。
   • 用于最大池化或比较等运算的 位分解。
   • 为什么它很重要： 显着减少了约束的总数，从而减少了证明大小和 CPU 工作。
3. 证明后端
   • 它做什么： 使用带有多项式承诺的 Halo2 风格的证明系统来生成和验证证明。
   • 为什么它很重要： 提供 亚线性验证 和 简洁的证明，即使对于中等大小的模型，zkML 也变得实用。
4. 证明者和验证者 API
   • 它做什么： 公开简单的 CLI 命令和库调用：
   • ezkl compile 用于构建电路，
   • ezkl prove 用于为给定的输入生成证明，
   • ezkl verify 用于根据公共输出来检查证明。
   • 为什么它很重要： 降低了准入门槛——开发人员只需进行最少的代码更改即可将 zkML 添加到他们的工作流程中。

这些组件协同工作，将标准的神经网络推理转换为保护隐私、易于验证的证明，而无需开发人员成为密码学专家。

TikTok — 无需信任的认证验证

机密计算和远程认证

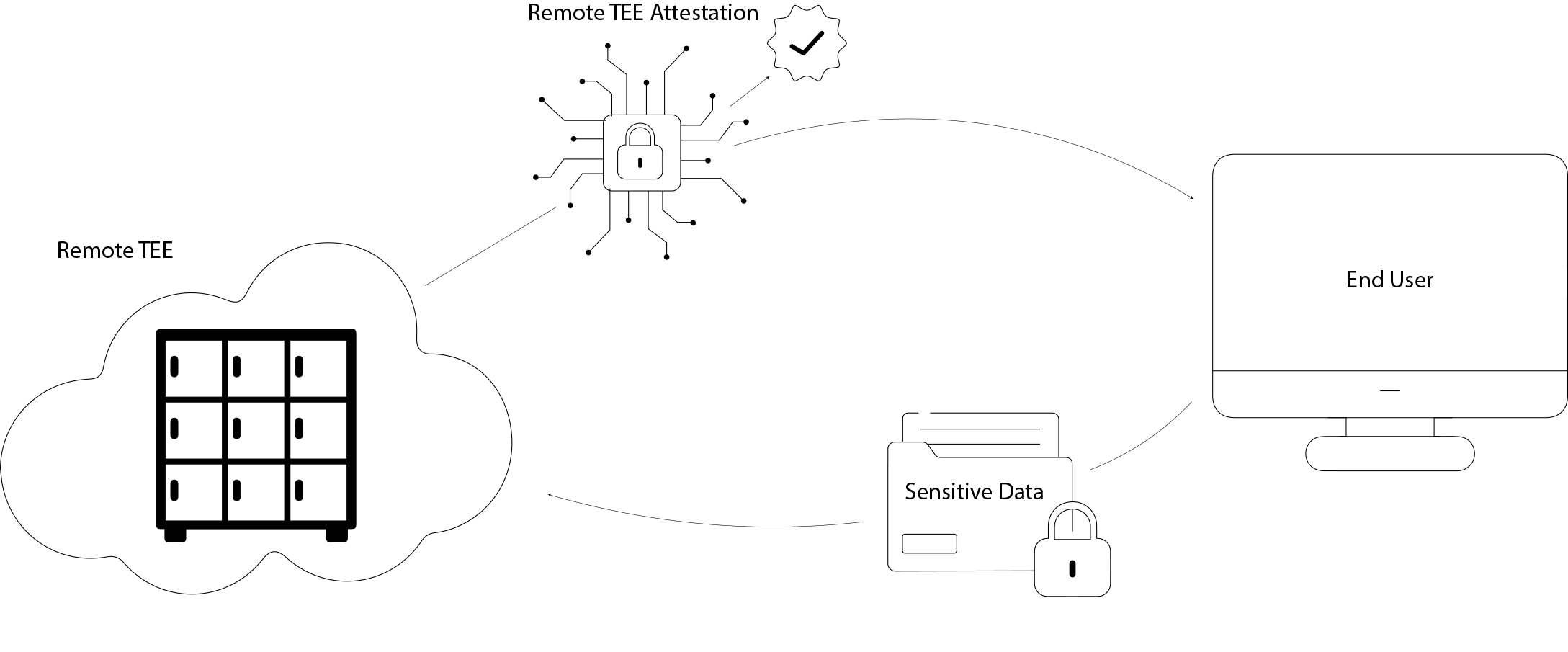
诸如 Intel SGX 或 AMD SEV 之类的可信执行环境 (TEE) 创建了硬件强制执行的“飞地”，其中敏感代码和数据受到保护——甚至免受云提供商自己的操作系统的影响。为了确保你正在与真正的飞地进行通信，云提供商提供 远程认证 (RA) 服务：你发送飞地的证据（证书、固件哈希、PCR 值），RA 服务会根据供应商根验证它并返回一个简单的“确定”或“失败”。

扩大的信任边界

依赖 RA 服务会将信任从仅仅 CPU 供应商转移到 供应商和云提供商的认证逻辑。

• 软件错误： RA 服务中的一个错误可能会接受恶意或过时的飞地。
• 内部威胁： 如果 RA 服务器受到攻击，攻击者可以伪造认证。
• 中心化风险： 所有依赖方共享相同的认证预言机；他们必须信任其完整性和可用性。

目标：无需信任的认证验证

我们想要 消除 信任 RA 服务器本身的需求。飞地（或另一个不受信任的服务）不是盲目地接受是/否响应，而是生成一个 零知识证明，该证明直接显示：

1. 针对原始 TEE 证据执行的确切 RA 验证代码
2. 检查了所有证书链，固件哈希匹配，并且 PCR 值已验证
3. 未泄露任何敏感证据（证书、测量结果或密钥）——仅泄露检查已通过的事实

有了这样的证明，任何依赖方都可以独立且安全地验证飞地的真实性，从而将信任边界缩小到仅硬件供应商。

TikTok 的无需信任的认证验证

TikTok 的解决方案将传统的远程认证过程转换为透明的零知识证明，从而消除了信任中心化认证服务器的需求。以下是它的高级工作原理：

• 原始 TEE 证据作为输入

飞地生成其通常的认证证据——来自硬件供应商的证书链、固件测量值和 PCR（平台配置寄存器）值。此原始数据是证明系统的输入，但永远不会以明文形式出现在验证者面前。

• Circom 电路对验证逻辑进行编码

TikTok 实现了与你在远程认证服务中期望的相同的验证步骤——根据供应商根密钥检查每个证书的签名，比较固件哈希，并验证 PCR 寄存器——作为 Circom 算术电路。每个条件和密码学检查都变成了一系列模运算约束。

• zkSNARK 证明生成

使用标准 SNARK 框架（例如，通过 snarkjs 的 Groth16），证明者编译 Circom 电路，运行可信设置，然后生成简洁的证明。此证明证明“我在此证据上运行了认证验证器代码，并且每个检查都已通过”，而不会泄露任何证书、哈希或 PCR 值本身。

• 公共验证

任何依赖方——无论是客户服务后端、区块链智能合约还是另一个飞地——都可以加载公共验证密钥并有效地验证 SNARK 证明。结果是关于飞地真实性的简单是/否决定，而无需对远程服务器的隐藏信任。

通过将远程认证重铸为 TEE 证据的零知识证明，TikTok 的方法将信任恢复到仅硬件供应商。它弥合了强大的硬件保证与对软件服务的最小信任需求之间的差距，同时保留了认证数据的机密性。

以下是 Circom 模板 validate_x509_rsa，它实现了 X.509 证书的端到端 RSA-PSS 签名检查。

template validate_x509_rsa(word, number_blocks, e_bits, hash_len, tbs_certificate_len) {
  // uint8_t modulus[512];
  signal input modulus[512];
  // uint8_t tbs_certificate[tbs_certificate_len];
  signal input tbs_certificate[tbs_certificate_len];
  // uint8_t signature[512];
  signal input signature[512];

  // constraining modulus and signature to byte values (0–255).
  // 将模数和签名约束为字节值 (0–255)。
  component modulus_bytes[512];
  component signature_bytes[512];
  for (var i = 0; i < 512; i++) {
    modulus_bytes[i] = Num2Bits(8);
    signature_bytes[i] = Num2Bits(8);
    modulus_bytes[i].in <== modulus[i];
    signature_bytes[i].in <== signature[i];
  }

  // Modulus needs to be reversed (i.e., converted to little-endian).
  // 模数需要反转（即，转换为小端）。
  signal modulus_little_endian[512];
  component reverse_modulus = reverse_bytes(512);
  reverse_modulus.in <== modulus;
  modulus_little_endian <== reverse_modulus.out;

  // Signature needs to be reversed (i.e., converted to little-endian).
  // 签名需要反转（即，转换为小端）。
  signal signature_little_endian[512];
  component reverse_signature = reverse_bytes(512);
  reverse_signature.in <== signature;
  signature_little_endian <== reverse_signature.out;

  // Convert the modulus and signature into uint64_t arrays.
  // 将模数和签名转换为 uint64_t 数组。
  component modulus_qwords = bytes_to_qword(512);
  component signature_qwords = bytes_to_qword(512);
  modulus_qwords.buf <== modulus;
  signature_qwords.buf <== signature_little_endian;

  // Compute the SHA384 hash of the content to be signed.
  // 计算要签名的内容的 SHA384 哈希。
  // The whole TBSCertificate is hashed using the algorithm specified in the signature algorithm field.
  // 整个 TBSCertificate 使用签名算法字段中指定的算法进行哈希处理。
  component sha384_hasher = Sha384_hash_bytes_digest(tbs_certificate_len);
  sha384_hasher.inp_bytes <== tbs_certificate;

  // Verify the signature.
  // 验证签名。
  component rsa_verifier = RsaVerifySsaPss(word, number_blocks, e_bits, hash_len);
  // Value is valid.
  // 值有效。
  rsa_verifier.modulus           <== modulus_qwords.out;
  rsa_verifier.sign              <== signature_qwords.out;
  rsa_verifier.message_hashed    <== sha384_hasher.hash_bytes;
}

致谢

本文借鉴了几个团队和项目的开创性工作：

• Google 的 “来自 ECDSA 的匿名凭证” 论文和 Google Wallet 中的实现，它启发了用于保护隐私的硬件支持凭证的 sumcheck + Ligero 方法。
• Cloudflare 的 zkAttest 项目，展示了零知识证明如何将 WebAuthn 认证转换为真正私有、无需信任的验证机制。
• EZKL，开源 zkML 工具包，它通过基于 Halo2 的证明使可证明的神经网络推理成为可能。
• TikTok 的 无需信任的认证验证，展示了用于远程 TEE 认证的零知识 SNARK 解决方案。

• 原文链接： hexens.io/blog/zk-usecas...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～