Paradigm CTF- BabyCrypto

  • bixia1994
  • 更新于 2021-08-05 23:50
  • 阅读 4176

前段时间跟行业内人士聊天的时候，聊到了一个有趣的话题，即以太坊中私钥，公钥和地址分别是什么关系？以及ECDSA是如何工作的？

前段时间跟行业内人士聊天的时候，聊到了一个有趣的话题，即以太坊中私钥，公钥和地址分别是什么关系？以及ECDSA是如何工作的？

正好在做Paradigm的CTF中，有一道关于ecdsa的题目，故借此题目将ecdsa和私钥，公钥等简单梳理下。

本文为原创文章，如需转载请联系作者。

本文的原创链接如下：https://t.1yb.co/y9r4 本文的主要参考文章有：

  1. 零知识证明 - 椭圆曲线基础
  2. Elliptic curves over real numbers and the group law
  3. Elliptic curves over finite fields and the discrete logarithm problem
  4. Key pair generation and two ECC algorithms: ECDH and ECDSA
  5. Algorithms for breaking ECC security, and a comparison with RSA

ECC, ECDSA

ECC是Elliptic Curve Cryptography的缩写，ECDSA是基于ECC的一种签名算法。

实数域上的ECC

实数域上的ECC是一组满足如下方程的点的集合

$$ y^2=x^3+ax+b\ 其中：4a^3+27b^2 \neq 0 $$

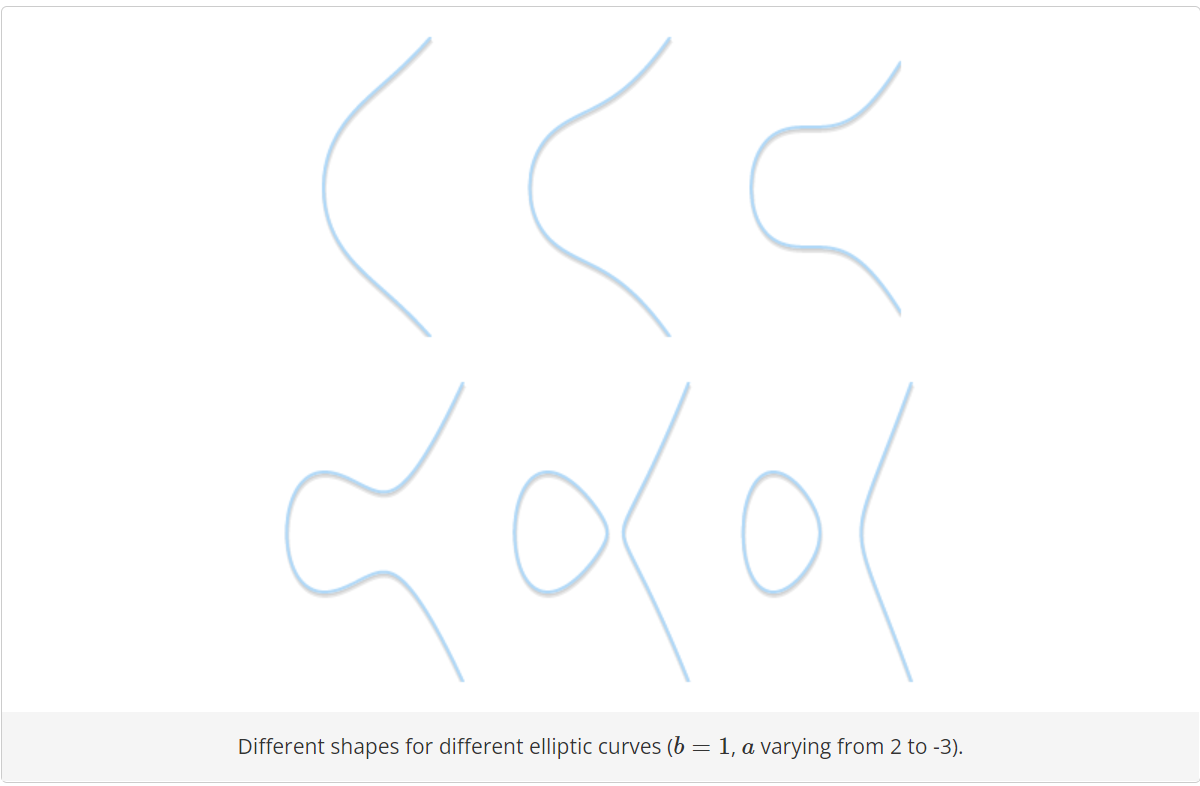
其形状如图所示，可以看到其曲线为一个X轴对称图形。 image20210804223829496.png

在如上图的曲线外，ECC还定义了一个位于无穷远处的点，并且规定该点为0点。0点加上上述方程，其所曲线上的所有点的集合即构成了ECC。

$$ \left{ (x, y) \in \mathbb{R}^2\ |\ y^2 = x^3 + ax + b,\ 4 a^3 + 27 b^2 \ne 0 \right}\ \cup\ \left{ 0 \right} $$

加法

在ECC中，加法定义为两个曲线上的点P,点Q的连成的直线与椭圆曲线的交点点R，满足如下关系：

$$ P + (Q + R) = Q + (P + R) = R + (P + Q) = \cdots = 0 $$

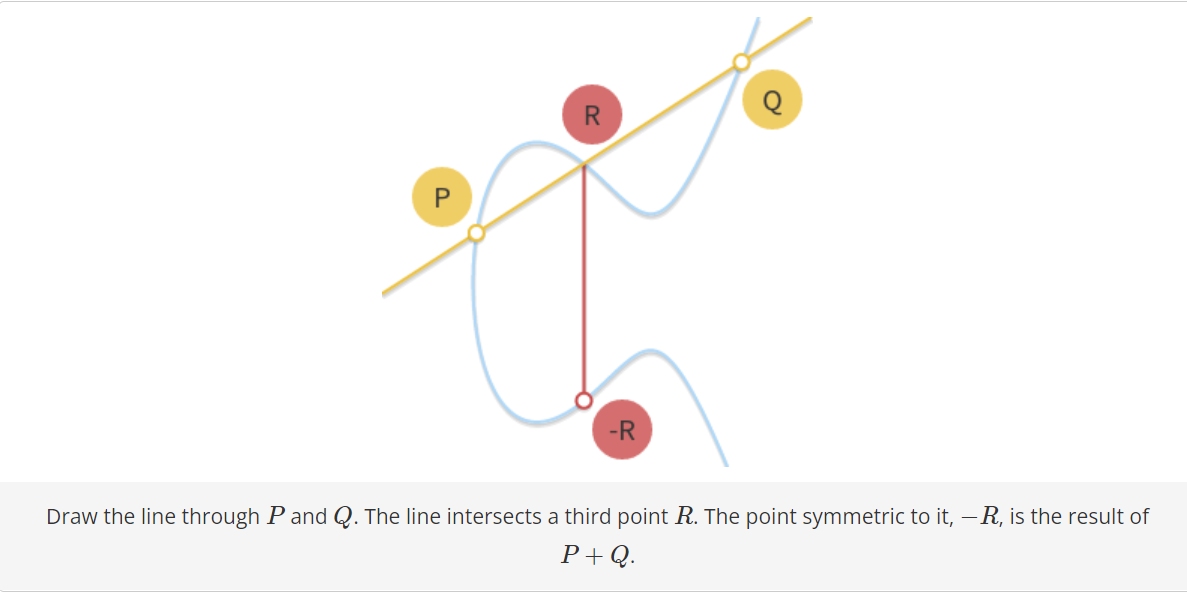
即直线与椭圆曲线上相交的三点之和为0. 如下图所示： $P+Q=-R$, 其中，$R$与$-R$点关于X轴对称。 image20210804224502068.png

在上述的加法定义中，需要明确如下的edge case：

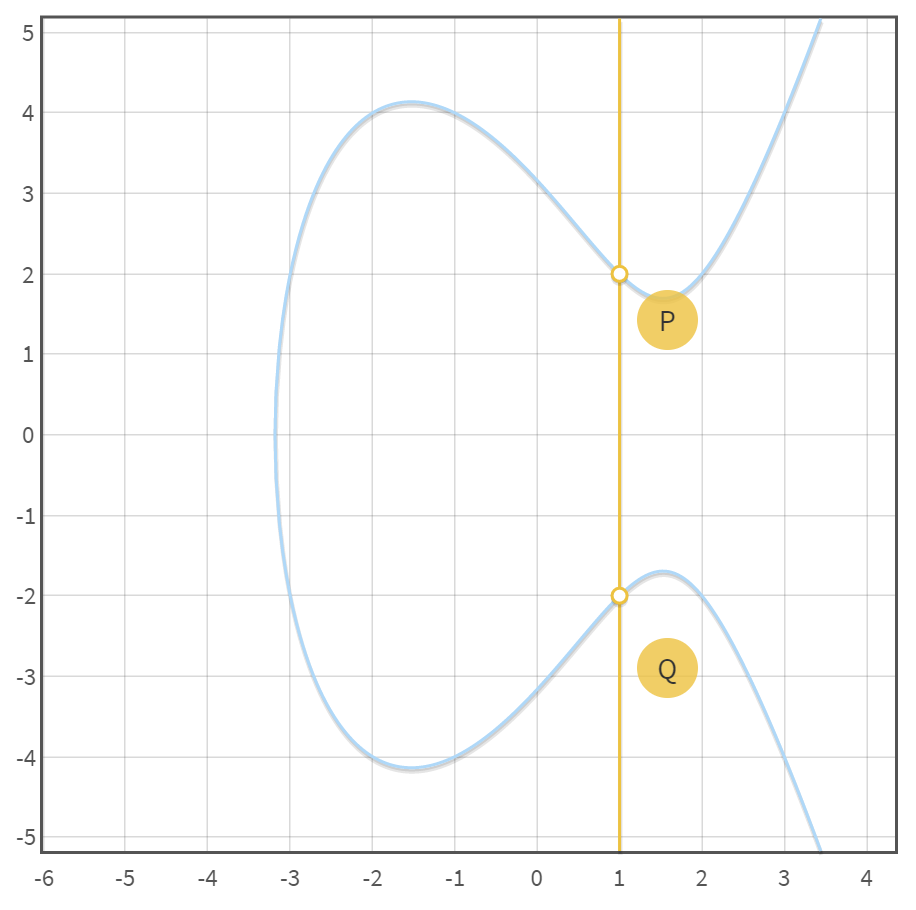
case 1: P点和Q点关于X轴对称

当$P$点和$Q$​点关于X轴对称时，此时直线为一条垂直于X轴的直线，于椭圆曲线只相交于2个点，则其和应定义为0点.

$$ P+(-P)=0 $$

image20210804225138089.png

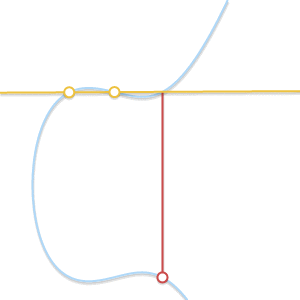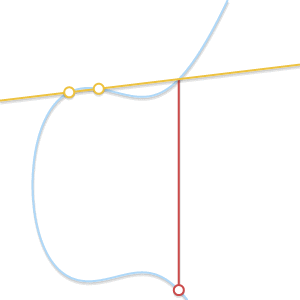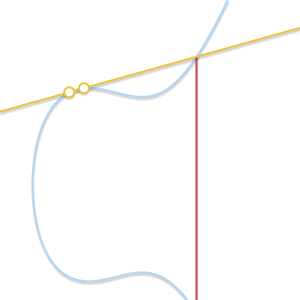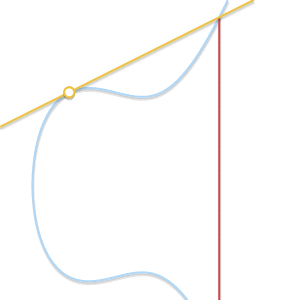
case2: P点和Q点是同一个点

此时直线为椭圆曲线在该点的切线，R点为P点所在的切线与椭圆曲线的交点。

$$ P+P=-R $$

animationpointdoubling.gif

乘法

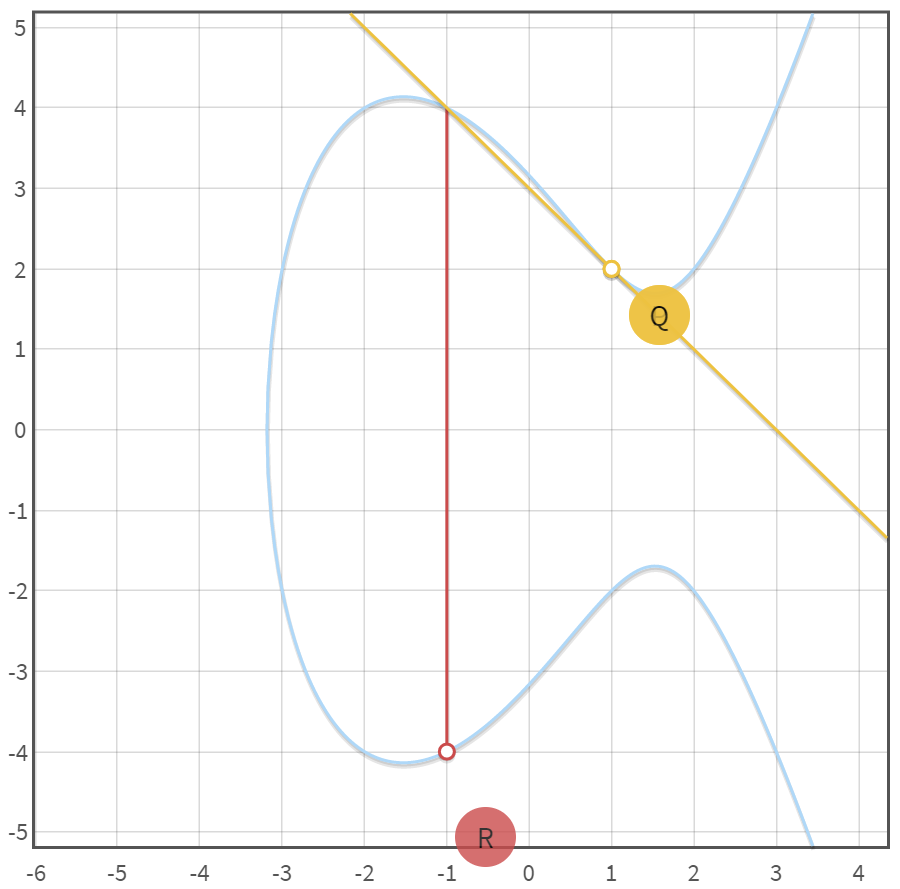
在椭圆曲线中，乘法被定义为同一个点的多次相加，即点P乘以n就等于点P与自己相加n-1次。

$$ nP = \underbrace{P + P + \cdots + P}_{n\ \text{times}} $$

image20210804230105822.png

为提高乘法效率，一种名为“double & add”，即翻倍再相加的算法被发明了出来：其思路可以简化为将n个P点依次累加，转换为将P点依次翻倍，然后将翻倍后的P点相加。

举个简单的例子：如计算151*P，可以将151转换为如下：

$$ 151 = 1 \cdot 2^7 + 0 \cdot 2^6 + 0 \cdot 2^5 + 1 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 \ = 2^7 + 2^4 + 2^2 + 2^1 + 2^0 $$

则：

$$ 151 \cdot P = 2^7 P + 2^4 P + 2^2 P + 2^1 P + 2^0 P \ 2^0 P = P \ 2^1 P = P+P\ 2^2 P = 2^1P + 2^1P\ 2^3 P = 2^2P + 2^2P\ 2^4 P = 2^3P + 2^3P\ 2^5 P = 2^4P + 2^4P\ 2^6 P = 2^5P + 2^5P\ 2^7 P = 2^6P + 2^6P $$

从上面的计算过程可以看到，乘法的效率是很高的, 时间复杂度为： $O(\log n)$。

然而其逆过程，称为对数问题，即已知P点和R点，且已知R点是P点乘以n后得到，要推断出n的值的问题。该对数问题是一个很难的问题

有限域上的ECC

前面我们简单讲了实数域上的ECC，主要定义了加法和乘法。并且知道了乘法的逆运算是一个很难的问题。但是我们在以太坊上面使用的ECC并不是定义在实数域，而是定义在有限域。

有限域

首先我们需要理解什么是有限域。一个简单的解释是该域中的所有元素都是某一个给定的素数的余数。如$\mathbb{F}_p$​​​​, 素数p=23时，该域中就只包含：0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22这些数，且其必须为整数不能为小数。（回忆下小学学的余数的概念~）

有限域中的加减乘除的运算：

加法：$(18+9)\ \%\ 23=4$​​​

减法：$(7-14)\ \%\ 23=16$​​

乘法：$(4\times7)\%\ 23=5$​​​

除法：$(1/9)\%\ 23=18$ , $9 \cdot 9^{-1} \bmod{23} = 9 \cdot 18 \bmod{23} = 1$​

有限域上的ECC定义

给定一个素数P，则有限域$\mathbb{F}_p$上的ECC定义为：​

$$ \begin{array}{rcl} \left{(x, y) \in (\mathbb{F}_p)^2 \right. & \left. | \right. & \left. y^2 \equiv x^3 + ax + b \pmod{p}, \right. \ & & \left. 4a^3 + 27b^2 \not\equiv 0 \pmod{p}\right}\ \cup\ \left{0\right} \end{array} $$

则根据有限域上的计算规则，原实数域上的椭圆曲线图像跟有限域的椭圆曲线图像不尽相同，可以看作是作如下变换得到：

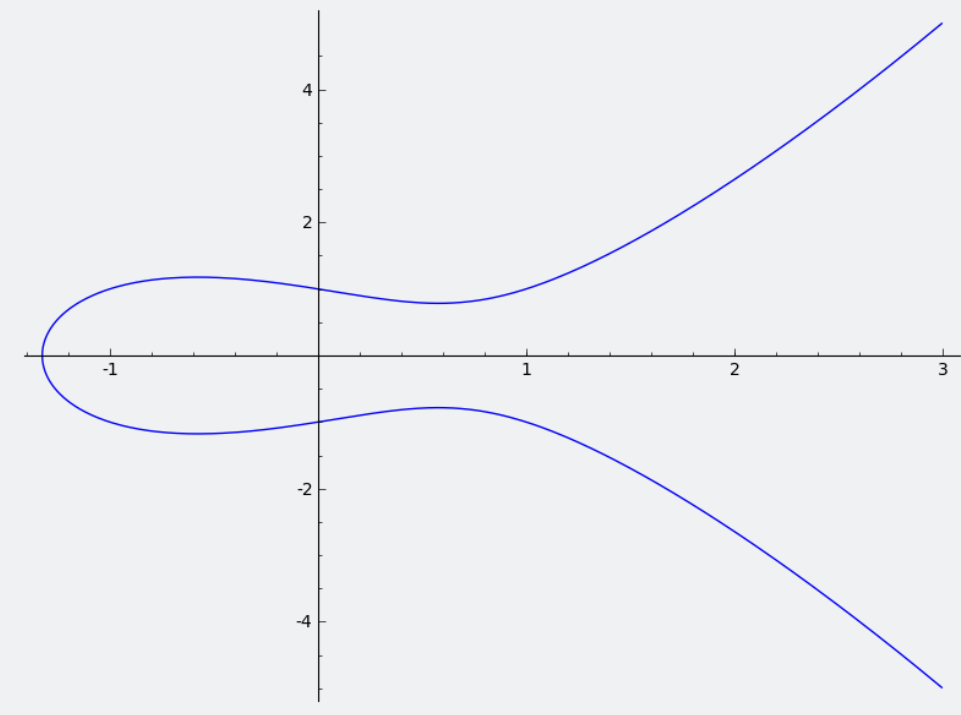
实数域上的y2 = x3 - x + 1图像 image20210805203154302.png

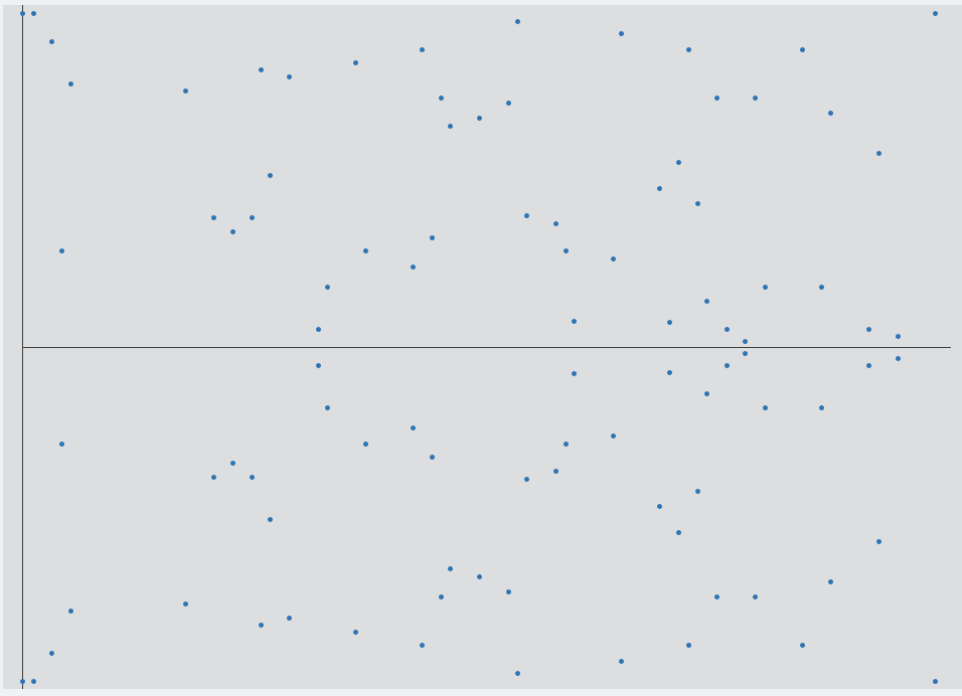
当P=97时的有限域上的图像： image20210805203301972.png

其特点是：关于中轴线对称，且由于取模算法的特性，每一个点的横纵坐标都是正整数，且小于素数P

有限域的加法：

有限域的加法与实数域上的加法定义类似，只是多了mod P. $ax + by + c \equiv 0 \pmod{p}$​​​,在根据有限域的特性，其会超出边界后重复，从而有限域上的直线类似于“贪吃蛇”，如下图所示。 ellipticcurvecryptimage01.gif

从另一个角度理解有限域的加法，可以认为有限域中的集合点构成一个三维空间的甜甜圈结构，其中的直线则是在甜甜圈的表面行走。具体解释可参考：https://www.youtube.com/watch?v=mFVKuFZ29Fc&list=PLN9KZDpNfsHMd7d7PX87JGesGY_Qzyb3V&index=2

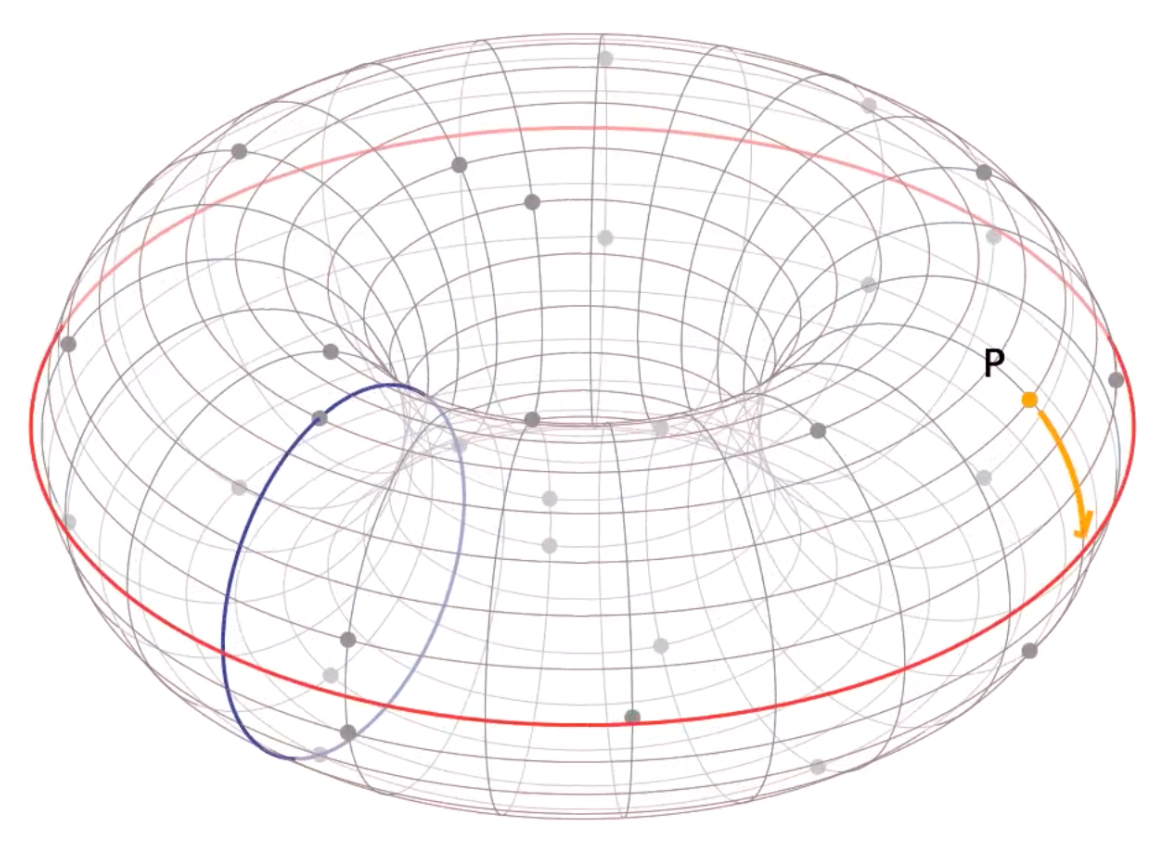
image20210805210206891.png

有限域的order

如上图，我们比较感兴趣的是当素数P=97时，有限域上椭圆曲线 $y^2 \equiv x^3 -x + 1 \pmod{97}$里所含有的所有的点的个数，这代表了这个集合的大小，称之为有限域的order。且存在一种快速计算有限域的order的算法 Schoof's algorithm.

有限域的乘法

与实数域的乘法类似，定义为：

$$ n P = \underbrace{P + P + \cdots + P}_{n\ \text{times}} $$

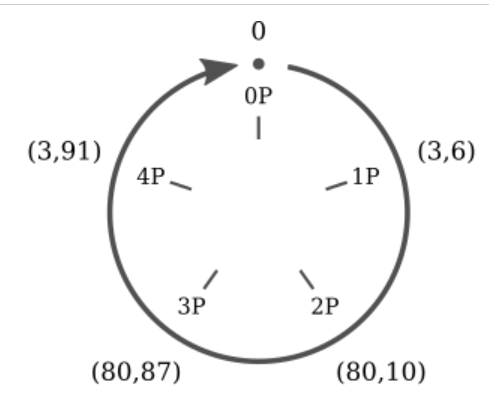
由于有限域特性（即对Y取模），故其乘法得到的结果最终会呈现一个环，表明针对某个特定的点，不断地从1乘到N，其得到的结果的点最终会重复，得到一个有限的集合。从该点相乘得到的点的集合称为subgroup。 image20210805211059987.png

局部有限域的点的数量

subgroup order对以太坊是一个很重要的概念，因为ECDSA签名就是基于一个subgroup order， 而不是一个完整的有限域的点。所以我们需要知道ECC对应的局部有限域的独立的点的数量。

根据拉格朗日定理，椭圆曲线在有限域上的总的点数量N, 和局部有限域的点数量n, 满足 $N \% n=0$， 即N是n的整数倍。故对于某一个特定的点Q，找到n的思路为：找到该椭圆曲线在素数P的有限域上的所有点N，从小到大列出N的所有整除因子，依次乘以点Q，找到最小的一个整除因子，满足nQ=0

例如，对于$y^2 = x^3 - x + 3$, 质数P=37, 则通过计算得知N=42，选择一个点(2,3),$ 42=1\times42=2\times21=3\times14=6\times7$​​, 依次​从[1,2,3,6,7,14,21,42]中取值，与(2,3)点相乘，发现最小的一个值 $ 7\times(2，3)=0$, 故n=7

选取最优基点

为保证局部有限域中的点的数量最大，我们需要选择一个最优的点作为基点。根据拉格朗日定理，定义$h = N / n$, 称为局部有限域的分组因子。又因为对于任何一个点都满足如下条件：

$$ N\times P=0 $$

故可以推导为：

$$ n\times h\times P=0 $$

要使得n最大，故取最小的h值，然后找到一个点P满足 $h\times P=0$. 该种方法真针对n是素数有效。

ECDSA

椭圆曲线的域名参数

根据上述定义，一个特定的椭圆曲线可以由如下6个参数完全确定，以太坊中选用了和比特币相同的椭圆曲线"secp256k1"

指明有限域大小的素数:
P=0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
椭圆曲线方程的系数: a = 0, b=7
产生我们子群的基点 base point: G(x,y)
G[x] = 0x79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
G[y] = 0x483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
子群的order: 
n=0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
子群的辅助因子 h=1

私钥

在以太坊中，私钥定义为一个长度为32bytes的数字。在椭圆曲线中，私钥对应的是Pri（将bytes32转换为一个正整数）。即该椭圆曲线的基点G乘以私钥得到公钥Pub。私钥必须要小于子群的order n。

$$ Pri < n\ Pub_x = Pri\times G_x\ Pub_y=Pri\times G_y $$

公钥

公钥即私钥乘以基点后得到的点Pub，将点Pub的x轴的值和Y轴的值拼接在一起，得到一个64位的数字，即为以太坊的公钥, 即：

$$ PUB=Pub_x\cdot pub_y $$

EOA的地址

将公钥取哈希得到哈希值的最右侧160位即为该私钥对应的地址：

$$ addr=keccak256(PUB)[-159:] $$

ECDSA交易签名函数

ECDSA是一种对交易信息的哈希值进行签名的函数，当Alice对交易签名后得到(r,s), 任何人都可以利用(r,s) 以及相应的交易信息的哈希值运算得到Alice的公钥，从而验证该交易是否是Alice发出的。

整体流程如下：

alice 构造一笔交易，交易信息如下：
[nonce,gasPrice,gasLimit,to,value,data,chainId,0,0] =>
[0,0x09184e72a000,0x30000,0xb0920c523d582040f2bcb1bd7fb1c7c1ecebdb34, 0, "",1,0,0]
RLP编码后得到的数据为：
其为list，按照list编码要求编码
nonce: 0 => 0x80 => len = 0x01
gasPrice: 0x09184e72a000 => 0x8609184e72a000 => len = 0x07
gasLimit: 0x30000 => 0x83030000 => len=0x04
to: 0xb0920c523d582040f2bcb1bd7fb1c7c1ecebdb34 => 0x94b0920c523d582040f2bcb1bd7fb1c7c1ecebdb34 => len = 0x15
value: 0 => 0x80 => len = 0x01
data: "" => 0x80 => len = 0x01
chainId,0,0 => 0x018080 => len = 0x03
最后整合为list，编码为:
0xe6808609184e72a0008303000094b0920c523d582040f2bcb1bd7fb1c7c1ecebdb348080018080
需要签名的交易哈希为：
keccak256(RLP([nonce...]))=901237a23fc304ddebc9d4f103a19bacc9fd7294bb1b7206a65cafa420804afa

拿到交易哈希后，alice选择一个随机数K，然后用随机数计算出临时点P，并用临时点P的X坐标值即为r值, 再对子群的order取模

$$ P=k\cdot G $$

$$ r=P_x \% \ n $$

然后用r值乘以Alice的私钥$d_A$,再加上交易哈希值的和，再乘以随机数K的导数得到s值, 再对子群的order取模

$$ s=k^{-1}\cdot(r\times d_A+z) \% \ n $$

ECDSA交易验证

验证ECDSA签名后的交易的基本思路是利用alice的公钥Ha，因为签名运算中用到了Alice的私钥$d_A$, 故验证时只需要用到公钥Ha.

对于椭圆曲线，给定横坐标x=r，可以算出对称的两个点R，R' . 再分别用R和R', 计算出可能的公钥Ha

$$ H_A=r^{-1}\cdot (sR-zG) \ H_A'=r^{-1} \cdot (sR'-zG) $$

证明如下：

$$ H_A = r^{-1} \cdot (sR-zG) \ H_A = r^{-1} \cdot (s\cdot k\cdot G -zG)\ H_A = r^{-1} \cdot (r\times d_A \cdot G + zG - zG )\ H_A = r^{-1} \cdot (r \times H_A) \ H_A = H_A $$

ECDSA的攻击利用

从上面的分析可以看到，我们再对一笔交易进行签名的时候，会首先生成一个随机数，然后利用随机数生成一个点P，利用点P的横坐标X的值作为r值，再利用r与私钥的乘机加上签名的信息之和除以随机数k，得到s值。这里的关键是需要生成一个随机数k，如果再签名过程中，随机数并不是随机生成的，而是有迹可循的，或者是固定的一个值，我们就可以通过以下方程推导出私钥$d_A$

$$ s_1=k^{-1}(r\cdot d_A+z_1)\ s_2 = k^{-1}(r\cdot d_A+z_2)\ s_1-s_2=k^{-1}(z_1-z_2)\ k=(z_1-z_2)(s_1-s_2)^{-1}\ d_A=(s_1k-z_1)r^{-1} $$

再本题目中，发现：ok和hi的签名信息中r值一样，说明随机数k一样

message? ok
keccak256("ok")=14502d3ab34ae28d404da8f6ec0501c6f295f66caa41e122cfa9b1291bc0f9e8
r=0xeac250f3dccb2eef0e7c4112807a61815fc61f4d241d5076fcad1b50629e9671
s=0xc2a39d1efc8f7fca69a3099deda8c2fbd4304e6cfee6dba075e1b9a0fbfa999d
message? hi
keccak256("hi")=7624778dedc75f8b322b9fa1632a610d40b85e106c7d9bf0e743a9ce291b9c6f
r=0xeac250f3dccb2eef0e7c4112807a61815fc61f4d241d5076fcad1b50629e9671
s=0xc070c31f27b4e4661b5a701d77bf5813e270b1ca28d7a56d366c30106f527b69

利用python算出私钥$d_A$：

def modDivide(a,b,m):
    a = a % m
    inv = modInverse(b,m)
    if (inv == -1):
        print("Division not defined")
    else:
        return (inv*a) % m
def modInverse(b, m):
    g = math.gcd(b, m)
    if (g != 1):
        return -1
    else:
        return pow(b, m-2, m)
def hash_mssage(msg: str) -> int:
    # hash the message using keccak256, truncate if necessary
    k = sha3.keccak_256()
    k.update(msg.encode('utf8'))
    d = k.digest()
    n = int(binascii.hexlify(d),16)
    olen = ecdsa.generator_secp256k1.order().bit_length() or 1
    dlen = len(d)
    n >>= max(0, dlen-olen)
    return n
if __name__ == "__main__":
    # msg1 = input("msg1? ")
    msg1 = "hi"
    msg1_hashed = hash_mssage(msg1)
    print(str(msg1_hashed))
    # msg2 = input("msg2? ")
    msg2 = "ok"
    msg2_hashed = hash_mssage(msg2)
    print(str(msg2_hashed))

    m = ecdsa.generator_secp256k1.order()
    # r1 = int(input("r1? "), 16)
    r1 = int("0xeac250f3dccb2eef0e7c4112807a61815fc61f4d241d5076fcad1b50629e9671",16)
    s1 = int("0xa8e72d180daf4d7f10778835719bb6de0abc003b94d71f28a99d673df4b06e17",16)
    s2 = int("0xab1a0717e289e8e35ec021b5e78521c5fc7b9cde6ae6555be912f0ce81588c4b",16)
    # s1 = int(input("s1? "), 16)
    # s2 = int(input("s2? "), 16)

    g = ecdsa.generator_secp256k1
    k = modDivide((msg1_hashed - msg2_hashed), (s1 - s2),m)
    d = modDivide(((s1 * k) - msg1_hashed), r1,m)
    print("d_A: ", d)
    test = input("test? ")
    test_hashed = hash_mssage(test)
    pub = ecdsa.Public_key(g, g * d)
    priv = ecdsa.Private_key(pub, d)
    sig = priv.sign(test_hashed, k)
    print(f"solved r=0x{sig.r:032x}")
    print(f"solved s=0x{sig.s:032x}")

点赞 2
收藏 1
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
bixia1994
bixia1994
0x92Fb...C666
learn to code

bixia1994

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！