带错误的学习

简介

我已经和一些安全人员进行过几次类似的对话：

他们：“我希望这种格（lattice）结构的东西能像 RSA 一样简单，我试着去了解它，但它太复杂了。”

我：“我认为 RSA 实际上比带错误的学习（Learning With Errors）要复杂一些，只是关于它的教学法还没有发展到那个程度。”

他们：*按下 X 表示怀疑*

我：“好吧，我来解释一下，违背我的意愿。我只想在这里说明，我基本上是被迫这样做的，并且从解释格密码学中没有任何乐趣。”

在做了几次之后，我觉得我应该把其中的一些内容写成更可扩展的形式。

先决条件：一点模算术和一点线性代数。

那么，格到底是什么？

格是一个自由的、有限生成的$\mathbb{Z}$-模，通常嵌入到有限维实向量空间中。

这有点拗口，所以让我们稍微分解一下。

模 这个术语只是数学家们卖弄学问，用一个不同的词来表示“向量空间，但基于环”（如果你不知道环是什么，对于这篇博文，只需将这个术语替换为$\mathbb{Z}$，即整数。它是一个可以进行加、减、乘运算，但不一定可以进行除运算的数字结构。如果你不记得向量空间是什么，它是向量存在的地方。你可以加向量，有一个零向量，并且可以用基环/域的元素乘以向量来缩放它们）。

有限生成 意味着存在有限数量的元素生成它，换句话说，我们模中的每个元素$x$都可以写成$x = \sum_{i=1}^n a_i g_i$，其中$a_i \in \mathbb{Z}$，$g_i$是我们的有限生成集。

这就剩下 自由 了。当一个模的行为像一个向量空间，并且不做任何奇怪的环操作时，它是自由的。模喜欢做奇怪的环操作，所以这个限定词非常必要。更正式地说，这意味着我们的模有一个基，也就是说，我们可以选择$g_i$，使上面的和是唯一的。在这种情况下，任何这样的集合都将具有相同的长度，我们称之为模的 秩 ，因为称它为维度会更有意义，我们可以将模重写为$\mathbb{Z}^n$。换句话说，对于任何环$R$，所有自由的、有限生成的$R$-模都同构于$R^n$。

所以我们有一些整数向量，我们想把它们嵌入到一个实向量空间中。为了避免一些技术细节，我只会讨论所谓的 满秩 格，即格的秩与向量空间的维度相同。我也不会深入研究 嵌入 的技术定义，这是一个相当不错的词，意思是格被放置在向量空间内。

需要注意的是，将$\mathbb{Z}^n$嵌入到$\mathbb{R}^n$中的方式不止一种。让我们以$n=2$为例，这样我们就可以画一些图。

格$\left\langle\left(1, 0\right),\left(0, 1\right)\right\rangle$

我们可以将$\mathbb{Z}^2$嵌入到$\mathbb{R}^2$中最简单的方法就是简单地平凡地映射事物，并查看所有具有整数坐标的点。毫不奇怪，我们得到了一个网格。

格$\left\langle\left(1, 0\right),\left(\frac12,\frac{\sqrt{3}}{2} \right)\right\rangle$

如果我们想更有创意一点，我们可以试试这种六边形图案。我们可以立即看出这两个格在本质上是不同的。例如，在第一个格中，每个格点都有四个最近的邻居，而在第二个格中，我们有六个最近的邻居。正如每个棋盘游戏爱好者都会告诉你的那样，这种差异很重要。非常重要。

创建二维格的方法还有很多。事实上，你可以通过观察二维格来证明关于椭圆曲线的各种各样的事情，但那是另一篇博文了。

所以总结一下：

• 格是$\mathbb{Z}^n$的一个副本，嵌入到$\mathbb{R}^n$中。
• 格具有基。它们的行为很好，并且不做奇怪的环操作。
• 格的嵌入方式很重要。

格中的难题

虽然格本身就很吸引人，但我们要做密码学，所以我们需要有难题。我们将要研究的两个难题被称为 最短向量问题 (SVP) 和 最近向量问题 (CVP)。

最短向量问题是问题“除$0$之外，这个格中最短的向量是什么”。零向量存在于所有格中，长度为 0，因此如果我们不排除它，它就不会是一个非常有趣的问题。

另一方面，最近向量问题回答了问题“给定一个向量$x$，不一定在格中，格中哪个点最接近这个向量？”

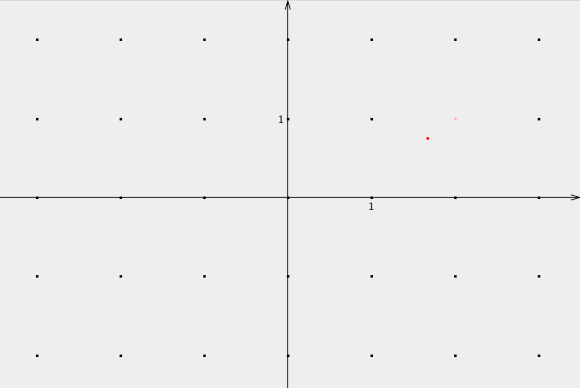
回答向量$\left(\frac53, \frac34\right)$ (红色)的 CVP (粉红色)

好基，坏基

起初，CVP 和 SVP 被认为是难题可能看起来很奇怪。毕竟，你甚至可能不需要拿出计算器或卷尺来解决这个 CVP 示例，而我甚至懒得证明 4 个邻居、6 个邻居的东西，这基本上就是 SVP，所以这有什么难的？

问题是，我们只在 2 维中观察了这个问题。但是对于格密码学，我们使用更像 768 维的东西。不幸的是，显卡很难渲染这些，所以我们将不得不通过数字来建立一些直觉。

在这个例子中，我们发现最接近$\left(\frac53, \frac34\right)$的向量是格点$(2,1)$。我的电脑是如何计算出这个最近向量的？好吧，我告诉它将$\frac53$四舍五入为$2$，将$\frac34$四舍五入为$1$。令人兴奋的东西。

让我们看看一个完全不同的格，由${(2,3),(5,7)}$生成的格。如果我们现在想知道最接近$(\frac53, \frac34)$的格点是什么，我们首先需要将基更改为我们的格基，四舍五入，然后再更改回标准基。我们看到$(\frac53, \frac34) = -\frac{95}{12}\cdot(2, 3) + \frac72\cdot(5, 7)$，四舍五入得到$-8\cdot(2,3)+4\cdot(5,7)=(4,4)$。让我们绘制它：

起点（红色）和“最近”点（粉红色）

等等，什么？首先，事实证明，这个完全不同的格与之前的格是同一个格，因为$(1,0)=-7\cdot(2,3) + 3\cdot(5,7)$和$(0, 1) = 5\cdot(2,3) -2\cdot(5,7)$。事实证明，我“无意中”使用了同一个格的不同基。但是为什么我们的四舍五入技巧不起作用呢？让我们倒退：我们的解决方案应该是$(2,1) = -9\cdot(2,3)+4\cdot(5,7)$。所以我们几乎到达了那里，但是四舍五入在第一个坐标中仍然偏离了 1。在 2 维中，这没什么大不了的，只需通过从每个坐标添加或减去 1 来暴力破解，看看是否能找到更近的点。当然，如果维度是 768 之类的，暴力破解就无济于事了。

这意味着有好基和坏基。在好基中，我们可以简单地对系数进行四舍五入来解决最近向量问题。但是，在坏基中，如果维度足够高，你就会彻底迷失方向。事实证明，坏基的数量超过了好基，如果你有一个好基并想要一个坏基，你只需随机更改一下基即可。（示例基是我第一次尝试）。

现在有一种方法可以使用称为格缩减的方法从坏基变为好基。但是这篇博文已经太长了，所以我不会深入研究。可以说，在高维度中获得足够好的基是很难的。

一个很难的问题，但只有当你不知道一些秘密时才会如此？这非常有希望，让我们做一些密码学！

我该如何用它加密？

有了所有这些格知识，我们可以直接深入研究带错误的学习。

作为参数，我们需要一个素数$q$和一个格秩$n$。流行的选择是像 3329 这样的素数和像 768 这样的秩。一个有点令人不快的注意的是，不幸的是，我们只会加密单个比特。

为了生成密钥，我们需要一个矩阵$A$，其中我们从 0 到 q 之间均匀随机地选择系数。理论上，该矩阵可以是公共参数，但是为每个密钥选择它使得不可能一次攻击所有密钥。

我们需要的下一个东西是两个向量，$s$和$e$，具有小的系数。在这里，小的通常意味着像 -1、0 或 1 这样的值。偶尔可能是 2，但不能更大。然后我们计算$t=A^Ts + e \mod q$并将$(A,t)$设为公钥，保留$s$作为私钥。

为了加密，我们需要另外两个向量$r$和$f$，也具有小的系数，以及一个小整数$g$。我们有点像密钥生成那样做，并计算$u = Ar + f \mod q$以及$v = t^Tr + m\cdot\frac{q-1}{2}+g \mod q$。为了建立一些直觉，让我们看看这些项的大小。由于我们乘以了一堆均匀分布的东西，$t$和$u$也是均匀分布的。如讨论的，$g$很小。$m\cdot\frac{q-1}{2}$要么是$0$，这是一个通常被认为相当小的数字，要么是$\frac{q-1}{2}$，这是一个模$q$是最大可能的数字（我们允许负数，所以如果我们让它更大，它只会回绕）。由于$t$是均匀分布的，因此$t^Tr$也是如此。这很好，因为这意味着它掩盖了我们的消息项是大还是小，并且只有一个消息位，我们最好尝试保护它。

那么我们如何解密呢？很简单，只需计算$m' = v - s^Tu \mod q$，如果它很小则输出 0，如果它很大则输出 1。由于

$$ \begin{align} m' &= v - s^Tu\ &= t^Tr + m\cdot\frac{q-1}{2}+g - s^T(Ar + f)\ &= (A^Ts+e)^Tr - s^T(Ar + f) +m\cdot\frac{q-1}{2}+g\ &= s^TAr - s^TAr + m\cdot\frac{q-1}{2} + e^Tr-s^Tf +g \end{align} $$

前两项相消。最后三项很小，更准确地说，不大于$2n$。所以当且仅当$m$为 1 时，$m'$才很大，至少只要我们选择的参数使得秩相对于素数不太大即可。

寻找格

所以你可能会说，这很好，但是格在哪里？所有关于最近向量和坏基的东西，看起来我们实际上没有使用任何东西。你是对的。格子有点奇怪，因为它们在算术数论中无处不在，但有时它们喜欢隐藏一点。所以让我们尝试打破这个方案来找到这个格。

我们想从公钥$A,t = A^Ts+e \mod q$中恢复私钥$s$。让我们分两步完成。首先，我们尝试找到任何向量$s'$和$e'$，它们求解$t=A^Ts'+e'\mod q$，而不关心它们是否很短，然后我们可以尝试修改它们使其变短。

我们可以将我们的方程重写为$(A^T, \operatorname{Id}, q\operatorname{Id})(s', e', k) = t$，其中$k$是一些整数向量，我们只是用它来避免担心$\mod q$部分。这是在整数上求解线性方程。它不像标准高斯算法那样简单，但是Smith的一个小修改将解决它，并给我们一个特殊解$(s', e', k)$和$(A^T, \operatorname{Id}, q\operatorname{Id})$的核的基。回想一下，任何解，包括我们正在寻找的短$s$和$e$，都与$s'$和$e'$相差核的一个元素。

嗯，更仔细地观察那个核，它通过是核而成为一个$\mathbb{Z}$-模，它有一个基，所以它是自由的，并且基是有限的，所以它是有限生成的。我们真的不关心最后$n$个系数，我们只需要它们来做模运算，但是我们可以直接删除它们，结果仍然是一个自由的，有限生成的$\mathbb{Z}$-模。鉴于我们想要找到短向量，并且我们对短的定义只是正常的欧几里德范数，我们可以简单地将这个核嵌入到$\mathbb{R}^{m}$中，并找到了一个格。事实上，我们已经找到了 这个 格，因为使用好基，我们可以找到核格中距离$(s', e')$最近的向量$(s_0, e_0)$，这意味着它们的差异会很短，并且确实会是$(s,e)$（即使不是，解密算法起作用的唯一属性是$s$和$e$很短，所以它只会解密）。

不幸的是，Smith 给我们一个非常大的特殊解和kernel basis向量，它们是kernel的一个非常糟糕的基，这意味着我们将无法找到这个最近的向量，这个属性赋予了 Learning With Errors 的安全性。

结束语

由于我们加密了一个单比特，如果我们按原样使用该方案，它将非常冗长，因为我们需要重复所有这些 128 次（或更多）才能实际传输密钥。Kyber（或 NIST 术语中的 ML-KEM）使用了一些技巧来缩小密钥和密文的大小并加快运算速度，但我不会在这篇博文中介绍它们。

此外，就像教科书 RSA 一样，我在此处介绍的算法在交互式设置中并不安全，并且需要额外的修改以确保我们无法通过发送多个相关消息并观察解密方使用相同或不同的密钥来提取私钥。但是这也需要一篇单独的博文。

• 标签 密码学, 格

• 原文链接： keymaterial.net/2023/09/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～