系绳上的证明：基于格的后量子SNARK与Greyhound - ZKSECURITY

信息

这是与 Archetype 合作完成的，其中 此帖子的白板版本已被录制。

随着量子威胁的逼近，我们需要开始考虑如何构建能够抵抗量子计算机的证明系统。这篇文章介绍了基于格的证明系统领域，并对最有希望的解决方案 Greyhound 的工作原理进行了高层次的解释。

从历史上看，部署我们现代的公钥密码基础设施几乎花费了 20 年的时间。要确保从当前广泛使用的密码系统平稳且安全地迁移到其抗量子计算的对应系统，将需要大量的努力。因此，无论我们是否可以估计量子计算时代到来的确切时间，我们都必须现在开始准备我们的信息安全系统，使其能够抵抗量子计算。– NIST Interagency Report 8105 (2016 年 4 月)

抗量子零知识证明的状态

到目前为止，我们知道只要增加对称密码的参数大小，它基本上是安全的。因此，不要使用 SHA-256，而是使用 SHA-512，不要使用 AES-128，而是使用 AES-256，等等。这就是为什么发布的第一个抗量子签名标准是基于哈希的 (PQCRYPTO: 长期安全抗量子系统的初始建议 (2015))，这也是为什么基于哈希函数的证明系统（如 STARK、Ligero、Aurora、Fractal、Brakedown 等）只要使用足够大的参数（今天的情况并非如此）就是安全的。

注意

请参阅 Grover 算法，了解为什么我们必须增加参数 https://www.youtube.com/watch?v=RQWpF2Gb-gU

另一方面，非对称密码正面临麻烦。最常见的非对称密码学是基于分解大数 (RSA) 或计算离散对数 (Diffie-Hellman) 的难度。这些问题对于量子计算机来说并不安全，我们需要找到替代方案。这包括我们所有基于椭圆曲线的 SNARK。

注意

请参阅 Shor 算法，了解为什么会这样 https://www.youtube.com/watch?v=lvTqbM5Dq4Q

想象一下，现在是十五年后。有人宣布他已经建造了一台大型量子计算机。RSA 死了。DSA 死了。椭圆曲线、超椭圆曲线、类群，等等，死了，死了，死了。– Daniel J. Bernstein (2016)

除了基于哈希的证明系统之外，最有希望的替代方案似乎是基于格的证明系统。这些证明系统基于格问题的难度，据信即使对于量子计算机来说也很难。

有趣的是，已经对该主题进行了大量的研究，并且结果已经很有希望。不仅证明规模小于基于哈希的证明规模，而且对 folding 的支持似乎也优于所有先前已知的方案（无论是在 SNARK 还是 STARK 中）。今年我们很幸运，所有 folding 团队都在提出新的基于格的方案：来自 protostar 的 Binyi 提出了 Latticefold+，来自 Nova 的 Srinath 提出了 Neo。

[LatticeFold] 是首次出现后量子 SNARK 系统实际上可能优于前量子 SNARK 系统的情况之一。– Dan Boneh 在 ZKProofs (2025)

在证明系统方面，许多方案都是在不稳定的假设下提出的，这些假设后来被打破，但最终收敛于基于强大假设并具有良好属性的方案。Greyhound 可能是该领域多年研究的结晶，并且它是第一个看起来既高效又可能对量子计算机安全的方案：它是透明的，具有线性证明者、亚线性验证者 (O(N)) 和 多对数证明大小。具体来说，它的证明大约是 50KB。

顺便说一句，与之前在基于格的 SNARK 中的许多研究不同，Greyhound 是一种多项式承诺方案 (PCS)，而不是整个零知识证明系统。这意味着它本质上可以与当今基于 PCS 的核心证明系统即插即用（基本上所有都是）。

此外，就在我写下这些文字的时候，一个 Rust 实现刚刚发布 (LattiRust)，而几周前，Ingonyama 宣布在其旗舰库 ICICLE 中支持 Greyhound。

格的简短介绍

思考格的一个好方法是首先思考向量空间，它是可以通过对一组向量（通常称为基）进行线性组合获得的所有可能向量的集合。如果向量是线性独立的（没有一个可以从组合其他向量中创建），并且你有足够的向量，那么你甚至可以跨越整个空间：

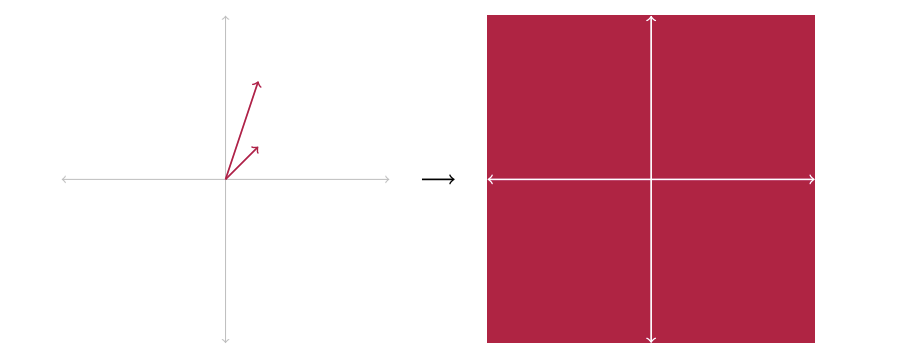
在向量空间中，我们可以用实数 (在 R 中) 缩放向量，但在格中，我们只能用整数 (在 Z 中) 缩放它们。这意味着格中的向量不是稠密的，而是形成更多的网格：

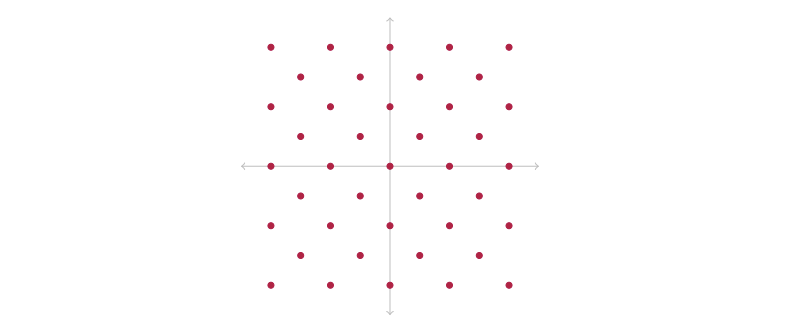
更严格的定义是考虑 k 个线性无关向量 bi 的所有线性组合（它们代表我们格的基）：

L:={∑i=0kzi⋅bi|z∈Zn}

注意

如果定义矩阵 B:=[b0|⋯|bk−1]∈Rn×k，其中 bi 作为列，则可以将上述内容重写为：

L:={B⋅z|z∈Zn}

我们认为在格中很难解决几个问题，即所谓的难题，我们在此基础上构建我们的密码系统。最著名的是最短向量问题 (SVP) 和最近向量问题 (CVP)，并且认为即使对于量子计算机来说，这些问题也很难解决。SVP 是关于在格中找到最短向量（除了零向量）：

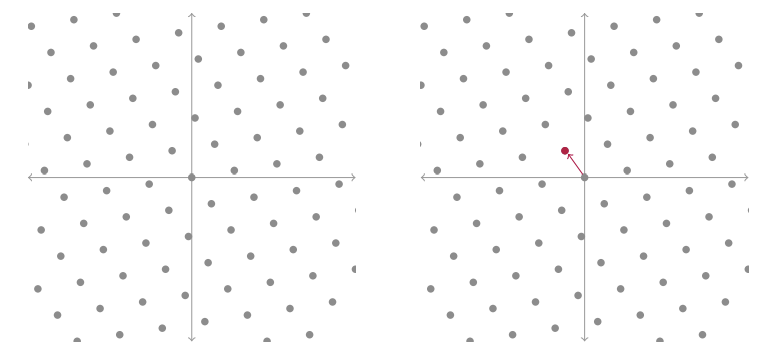
CVP 是关于找到给定非格点最接近的格向量：

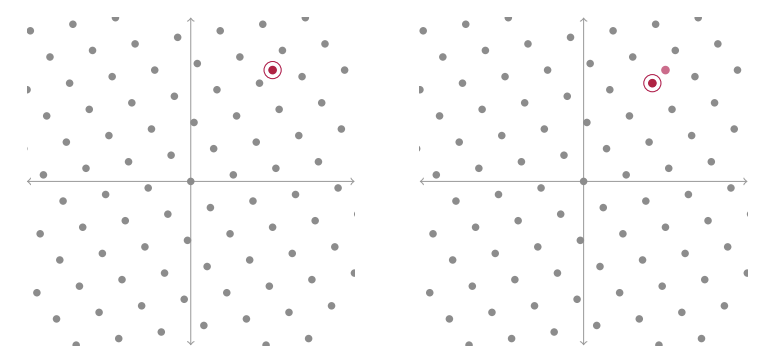
这两个问题都是最坏情况下的难题，这意味着它们并不总是很难，但对于一些经过专门设计的参数而言，它们是很难的。

但是对于我们的 PCS Greyhound，我们不会使用任何这些问题。相反，Greyhound 依赖于另一个称为模块短整数解 (M-SIS) 问题。

SIS 问题是关于找到矩阵中向量的线性组合，该组合导致零向量。该线性组合不能是微不足道的（即，它不能是零向量），并且标量必须很小（即，它们必须小于某个定义的边界）。

更严格地说，如果我们有一个在 𝕢Zq 中具有条目的格 B，那么它是关于找到一个向量 x→，使得 Bx→=0→modq 且 ||x→||≤β，对于一些已知的边界 β 和一些定义的范数运算 |||˙|，我们将在本文中忽略它。

M-SIS 问题是相同的，只是我们不使用 Zq 中的条目，而是使用多项式环 Rq 中的条目。对于本文中的大多数解释，如何定义环的确切定义并不重要。你可以假设该环的元素看起来像度数小于 64 且系数在 Zq 中的多项式，对于大约 232 的素数 q，但即使这对于从高层次理解协议而言也不重要。

Ajtai 在 1996 年表明，如果你可以打破平均情况下的 SIS（和 M-SIS）问题（从一些给定的分布中采样的随机实例），那么你可以打破最坏情况问题 SVP 的实例（最难解决的实例）！这意味着要么 SIS 是安全的，要么 SIS 被打破，但 SVP 也被打破。这种安全性降低提供了一种双赢的局面：如果它成立，我们将获得对密码方案的保证，如果它失败，我们将获得对数学的深入了解，并可能取得突破。

这是一个非常强的属性，与最坏情况下的难题（如 SVP 和 CVP）不同，它可以更轻松地构建密码系统，因为它们的安全性可以依赖于随机生成的实例（从一些分布中采样）。

Greyhound 的核心：Ajtai 承诺

现在让我们深入了解 Greyhound 的工作原理。请记住，Greyhound 是一个 PCS，因此我们从一个多项式 f 开始，我们将不得不对其进行承诺。

第一步是将我们的多项式 f 视为一个分块的多项式：

f(x)=f0+f1⋅x+f2⋅x2+f3⋅x3+f4⋅x4+⋯=f0′(x)+x4f1′(x)+x8f2′(x)+⋯

其中：

• f0′(x)=f0+f1⋅x+f2⋅x2+f3⋅x3
• f1′(x)=f4+f5⋅x+f6⋅x2+f7⋅x3
• ...

然后我们可以将我们的多项式编码为一个矩阵，其中系数插入到列中：

[f0f4f8f12f1f5f9f13f2f6f10f14f3f7f11f15]

我们的多项式现在几乎可以进行承诺了。

为了承诺多项式，Greyhound 依赖于 Ajtai 承诺。Ajtai 承诺的工作原理是取一个短向量 s→ 并将承诺计算为 t→=A⋅s→。

注意

A 矩阵是一个公共参数，可以从种子生成。因此，无需将整个矩阵保存在内存中，也无需可信设置。此外，这种矩阵通常看起来很宽但很短，这意味着它们有很多列但没有很多行。这是因为矩阵的秩决定了承诺的大小，并且维度必须对此进行补偿。

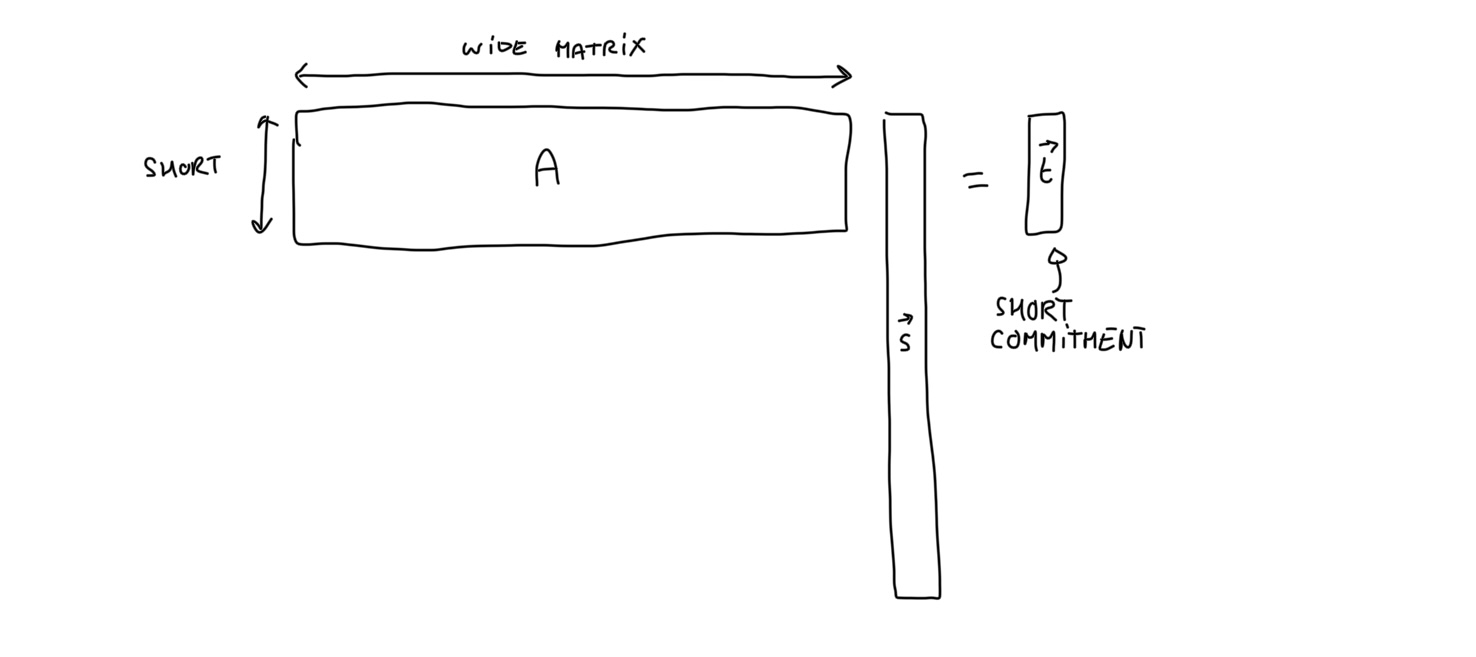
你可以很快看到这样的方案是 binding 的，因为如果你可以找到对同一承诺的两个不同的 opening，那么你就可以打破 SIS：如果你有 s→≠s′→ 使得 As→=As′→ 那么 A(s→−s′→)=0→ 并且你已经找到了 SIS 问题的非平凡解。（此外，它们对于加法来说是微不足道同态的，这与 folding 方案很好地配合。）

由于我们的多项式系数 fi 不一定是“小的”，因此我们实际上不能使用 Ajtai 承诺方案按原样承诺它们。因此，我们必须在承诺之前对它们进行基分解。例如，考虑二进制分解。Greyhound 论文使用函数 G−1 来执行分解，因此我们将使用它：t→=A⋅G−1(s→)，你可以想象有一个向量 G=[1248⋯] 可以重组分解向量 G−1(s→)。

这实际上有点烦人，而且 Greyhound 中的大部分复杂性都来自于必须处理非短向量。在本文中，我们有时可能会忽略（有意或错误地）分解和重组步骤，但严格的分析或可用的实现必须确保处理好这一点。

现在想象一下，我们的多项式矩阵的每一列都根据上述解释分解为某个基中的短向量 s→i。这意味着我们现在有以下矩阵 [s→0s→1s→2s→3]，它表示列中分解的多项式系数。

评估协议

如果没有在不同点评估多项式的好 PCS 是什么？ 让我们使用我们的系数矩阵编写 f 在 x 处的评估：

[1xx2x3]⋅[f0f4f8f12f1f5f9f13f2f6f10f14f3f7f11f15]⋅[1x4x8x12]=[f0′(x)f1′(x)f2′(x)f3′(x)]⋅[1x4x8x12]=f(x)

如果你不相信这是可行的，我们邀请你自己写下结果。请注意，这种技术实际上用于其他一些证明系统（aurora、fractal、hyrax、ligero、vortex、brakedown 等）。

然后 Greyhound 协议让证明者首先计算矩阵乘法的左半部分：

w→=a⊤⋅G⋅[s→0s→1s→2s→3]

然后让验证者自己计算另一部分：

y=⟨w→,b→⟩

对于评估点 x，其中 y=f(x)

当然，这是不安全的，因为验证者不知道左乘 w→ 的结果是否计算正确。

重要

在上面的协议中，验证者通过仅计算右乘来减少了工作量。例如，可以选择一个大小约为 N×N 的矩阵，其中 N 是多项式 f 的度数。使用这样的参数，验证者只需要做 N 的工作量，这是亚线性的，我们喜欢这样！证明者还发送了 w→，其大小约为 N，这是一个亚线性证明大小。

注意

这里 N=16，我们确实选择了 r=N=4（其中 r 是重数或矩阵的宽度），并且选择了 m=4（其中 m 是秩或矩阵的高度）。

使用类似 Schwartz-Zippel 的矩阵检查来修复协议的安全性

为了解决该问题，验证者可以发送一些 challenge c→。在证明者通过将评估 y 和“左侧计算”w→ 发送给验证者之后，需要发送这些 challenge。

使用 Schwartz-Zippel 引理，证明系统在单个随机点检查多项式恒等式（即，多项式 f 等于另一个多项式 g）。这可能发生在明文中，也可能隐藏在承诺中（例如 KZG）。使用这个 challenge 向量 c→，证明者可以向验证者表明，计算是在随机线性组合而不是单个向量中正确完成的。因此，可以将此视为类似 Schwartz-Zippel 的矩阵检查。

为此，证明者提供以下“opening”z→：

z→=[s→0s→1s→2s→3][c0c1c2c3]

然后验证者可以通过计算来检查 z→ 是否计算正确：

Az→=?∑ic→i⋅t→i

然后从 s→i 使用承诺 t→i 正确计算 w→：

⟨w→,c→⟩=?⟨a→,z→⟩

证明者发送了大小为 O(N) 的 w→，以及大小为 O(N) 的 z→。

更小的承诺插曲

在上面的协议中，多项式的承诺是 Ajtai 承诺 t→i 的列表。这是一个大小为 O(N) 的承诺，这不是很棒。为了减小该承诺的大小，Greyhound 使用了一个额外的“外部”承诺，该承诺将所有先前的承诺（他们称之为“内部”承诺）提交到单个承诺 u→ 中。

在我们的协议中，这意味着证明者生成承诺为：

u→=Bt^

其中：

• B 是一个单独的公共矩阵，类似于 A，用于外部承诺
• t^ 是所有分解的 t→i（即 G−1(t→i)）的串联

这意味着在我们的评估协议中，证明者还需要将 openings t→i 发送给验证者（每个大小约为 N），并且验证者需要通过检查来验证 t→i 是否正确

B[G−1(t→1)G−1(t→2)⋯]=u→

请注意，证明的大小仍然是 O(N)，并且验证者工作量仍然是 O(N) 也是。

Greyhound 的早期品种：LaBRADOR

人们可以在这里停下来，获得 O(N) 的证明大小和 O(N) 的验证者工作量，但是我们可以使用 LaBRADOR 将证明大小提高到多对数，而无需更改亚线性验证者时间 (O(N))。

LaBRADOR 是来自 IBM 研究院的同一团队的 早期论文，介绍了两件事：

1. “主关系”的证明系统
2. 将 R1CS 约束系统简化为该证明系统

主关系定义为证明对于以下形式的许多函数 f，证明者知道一个短向量列表 s→i′（与 Greyhound 无关），使得：

f(s′→0,s′→1,⋯)=∑1≤i,j≤ra′→ij⟨s′→i,s′→j⟩+∑i=1r⟨φ→i,s′→i⟩+b′→=0→

LaBRADOR 证明者说服验证者，无需发送 s→i′ 向量，而是发送更小的东西（并让验证者验证它是否通过了该主关系）。

如果能够将 Greyhound 中的内容简化为 LaBRADOR 的主关系，那就太好了，这样我们就不必发送我们的大证明元素（w→,t→,z→），而是发送更小的东西（并获得亚线性证明大小）。

具体来说（这为我们简化了事情），Greyhound 仅使用 LaBRADOR 主关系的一个子集：

∑i=1r⟨φ→i,s→i′⟩+b→′=0

注意

另一种看待它的方式是 LaBRADOR 是这种关系的证明系统，虽然它的 API 非常通用，但我们只需要使用它的一个子集。

这类似于看到以下矩阵乘法，其中 s→i′ 的向量很短：

[φ→0⊤φ→1⊤⋯⋯]⋅[s→0′s→1′⋯]=−b→′

因此，如果我们可以将 Greyhound 中的内容调整为这样，我们就可以成功了。

在这一点上，我们将不再讨论 LaBRADOR。如果你喜欢这篇文章，你可以向我们索要一篇关于 LaBRADOR 的文章 :)

将 Greyhound 拟合到 LaBRADOR 中

准备好最后一英里了吗？让我们首先回顾一下作为 Greyhound 中的验证者我们必须做什么：

1. 完成评估的计算并检查其是否正确：⟨b→,w→⟩=?y
2. 验证 w→（左矩阵乘法）是否计算正确：⟨c→,w→⟩=?⟨a→,z→⟩
3. 验证 z→ 是否计算正确：∑ici⋅t→i=?Az→

提示

接下来，我们需要使用 Kronecker 积 ⨂。如果你不知道此运算符的工作原理，你可以通过以下示例进行猜测：

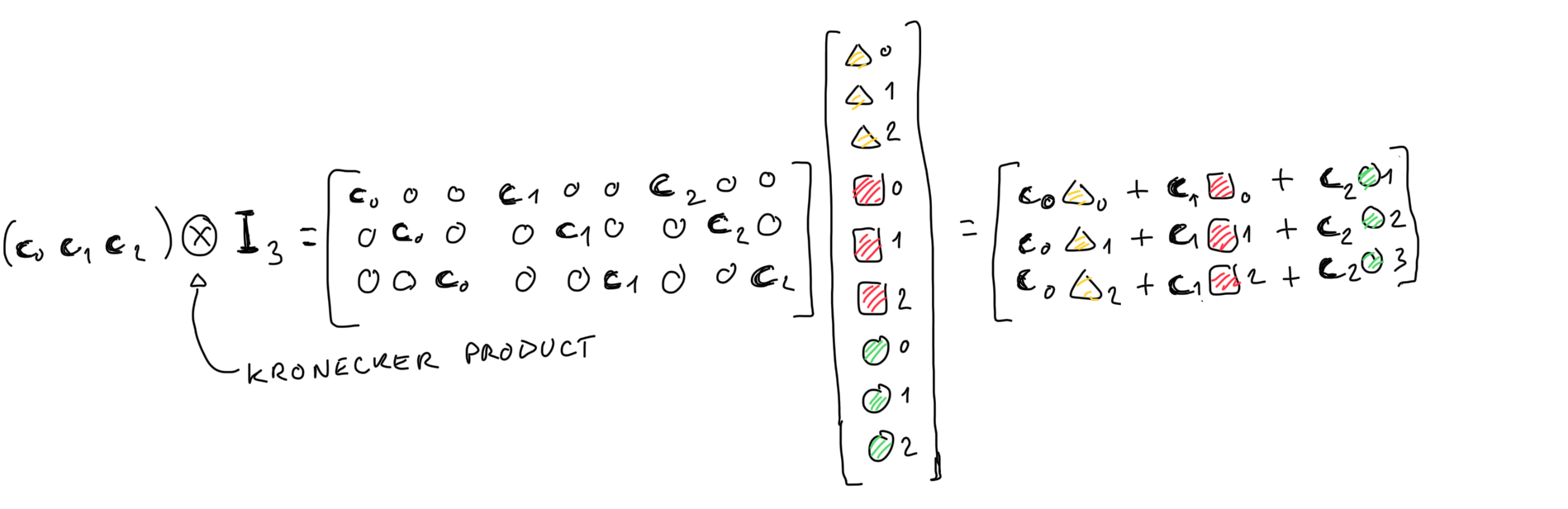
现在，如果我们定义 t→ 作为所有 t→i 的串联，我们可以将验证者必须执行的所有检查写为矩阵乘法：

[b→⊤0→0→c→⊤0→−a→⊤0→c→⊤⨂I−A]⋅[w→t→z→]=[y0→0→]

你可能已经开始看到这看起来像写为矩阵乘法的主关系。我们只需要：

• 将向量 [w→t→z→] 视为相同大小（假设为 n）的向量 s→i′ 的串联
• 将矩阵的每一行视为相同大小 (n) 的 φ→i⊤ 的串联

这几乎看起来像 LaBRADOR 的接口！如果我们能将其传递给 LaBRADOR，它将通过允许我们不必发送 w→,t→,z→ 来给我们带来更好的证明大小，这显然很大（尤其是 t→！）

我说几乎，因为我们的向量 [w→t→z→] 实际上并不短，而 LaBRADOR 期望这里有一个短向量。因此，接下来，让我们确保每个子向量都很小！

使 t→ 变小

我们可以使用分解的 t→ 代替：t^=G−1([t→0t→1⋯])

哦，顺便说一句，请记住，验证者所拥有的只是这些的承诺作为 u→。因此，我们还必须添加这些 opening 的验证：

[0→B0→b→⊤0→0→c→⊤0→−a→⊤0→c→⊤⨂G−A]⋅[w→t^z→]=[u→y0→0→]

使 w→ 变小

为了使 w→ 部分更小，我们可以使用分解的 w^=G−1(w→)。仅仅这样做是不够的，我们还需要确保证明者在收到验证者的 challenge 之前提交到该承诺（由于如果不这样做通常会出现的可靠性问题）。因此，证明者将发送一个小承诺 v→=Dw^（对于一些公共矩阵承诺 D）而不是 w→，并且验证者需要检查 opening w^ 是否匹配：

[D0→0→0→B0→b→⊤G0→0→c→⊤G0→−a→⊤0→c→⊤⨂G−A]⋅[w^t^z→]=[v→u→y0→0→]

使 z→ 变小

最后，缺少的最后一部分是使 z→ 部分变短。请记住，此向量计算为：

z→=[s→0s→1s→2s→3][c0c1c2c3]

其中，s→i 已经是短向量。解决方案是使用足够小的 challenge，以免增加向量的大小。在 Greyhound 论文中，challenge 是从多项式环元素中采样的，这些元素大多具有 0 系数，或者系数接近 0。

总结

最后，我们有以下矩阵乘法，其中包括验证者必须对公共值 (A,B,D,G)、语句值 (u→,a→,b→,y)、证明者值 (v→)、验证者值 (c→) 执行的所有检查，最后是见证向量 [w^t^z→]⊤：

[D0→0→0→B0→b→⊤G0→0→c→⊤G0→−a→⊤0→c→⊤⨂G−A]⋅[w^t^z→]=[v→u→y0→0→]

如上所述，对于证明者来说，剩下要做的就是将见证向量拆分为相同大小的子向量 s→i′，并且验证者必须将矩阵行拆分为相同大小的行。

希望你能理解这里发生的大部分事情。Greyhound 论文 介绍了更多同样重要的概念，因此，如果你想更深入地了解该协议，我们建议你花更多时间阅读该论文。

我们要感谢 Hoeteck Wee、Miha Stopar、Ngoc Khanh Nguyen，他们提供了帮助/反馈。

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～