邻近差距:发生了什么以及它如何影响我们的SNARKs
- zksecurity
- 发布于 2025-11-15 20:14
- 阅读 971
近期研究推翻了hash-based SNARKs的邻近差距猜想,该猜想用于设置参数。文章解释了这一结果对当前部署的SNARKs的影响,指出某些原本假定的安全参数实际上并不安全,需要调整参数以保证安全性,这可能会导致证明大小和验证时间的增加。

如果你一直在关注 ZK 领域,你很可能听说过最近涌现出的一系列反驳邻近间隙猜想的结果。这个猜想被用来设置基于哈希的 SNARK 的参数。因此,许多评论员迅速称其为对 SNARKs 的巨大打击。所以,最大的问题是:它到底有多糟糕?
在这篇文章中,我想给你一些关于发生了什么的直观理解,并解释这些结果如何影响当前部署的 SNARKs。我将尝试在不深入研究使我们所有协议成为可能的奇妙的月球数学的前提下做到这一点。如果你有兴趣学习月球数学,请告诉我们!一篇“邻近间隙 201”文章永远不会被排除。
在撰写本文时,一周之内发布了 6 篇与 Reed-Solomon 码和邻近间隙相关的论文:
-
Diamond 和 Gruen, 随机词距离分布研究,(ePrint)。
-
Crites 和 Stewart, 关于 Reed-Solomon 邻近间隙猜想 (ePrint)。
-
Bordage, Chiesa, Guan 和 Manzur, 所有多项式生成器都保持具有相互相关协议的距离 (ePrint)。
-
Goyal 和 Guruswami, 子空间设计码和(随机)Reed-Solomon 码的最佳邻近间隙 (ePrint)。
-
Ben-Sasson, Carmon, Haböck, Kopparty 和 Saraf, 关于 Reed-Solomon 码的邻近间隙 (ePrint)。
-
Chatterjee, Harsha 和 Kumar, Reed-Solomon 码的确定性列表解码 (ECCC)。
我将只关注反驳该猜想的论文。即上面的论文 1、2 和 5。为简短起见,我将使用作者的首字母来指代它们:分别为 DG、CS 和 BGHKS。
本文中使用的视觉效果和一些解释基于 Angus Gruen 在 ethproofs call #6 中展示的幻灯片。你也可以使用 Mahdi Sedaghat (Soundness Labs) 构建的这个可爱的交互式工具 来调整图表的参数。
在我们开始之前
为了理解发生了什么,让我们首先解释一下在所有新论文出现之前的最先进水平是什么。
在一个非常高的层面上,SNARKs 利用纠错码来引入冗余,并允许验证者在不读取证明者输入的全部内容的情况下检查属性。为了确保编码正确完成,SNARKs 还使用邻近测试。
SNARK 的效率和安全性取决于代码和邻近测试的参数。虽然有很多参数可以调整,但我们将重点关注:
- 代码的速率 ρ。这是衡量代码引入多少冗余的指标。准确地说,它是冗余量的倒数:ρ=1/2 意味着消息的编码比消息大 2 倍,ρ=1/4 意味着放大 4 倍,等等... 我们的 SNARKs 通常要求分母是 2 的幂,因此我们将重点关注 ρ 在 0 和 1/2 之间的值。
- 邻近测试的邻近参数 δ。这是一个介于 0 和 1−ρ 之间的值,是测试认为“远离”代码的阈值。对于熟悉相对汉明距离概念的读者:邻近测试经过调整,使得所有距离大于 δ 的输入都以高概率被拒绝。
为这些参数选择值需要平衡几个权衡。速率 ρ 设置了一个纯粹的性能权衡:证明者时间与证明大小和验证者时间。另一方面,邻近参数 δ 调整了性能与安全性的权衡。更大的 δ 值可以提供更好的证明者时间、验证者时间和证明大小!这是非常理想的。然而,数学上的最先进水平还不足以将 δ 设置为任意大。
下图显示了 ρ 和 δ 的所有可能选择,并定义了多个区域:
- 黑色区域表示无效参数。正如我们上面所说,δ 必须小于 1−ρ。
- 绿色和蓝色区域表示我们对其安全性有数学证明的参数集。这两个区域中的参数都保证邻近测试的输入要么 δ-接近代码,要么以高概率被拒绝。此外,绿色区域中的参数保证测试的输入接近唯一的码字。
- 白色区域中的参数具有未知的行为。我们没有证据表明它们会产生安全的邻近测试。在这个区域中操作代表着一种权衡:我们从使用更大的 δ 值中获得性能,但是我们失去了协议安全性的数学保证。
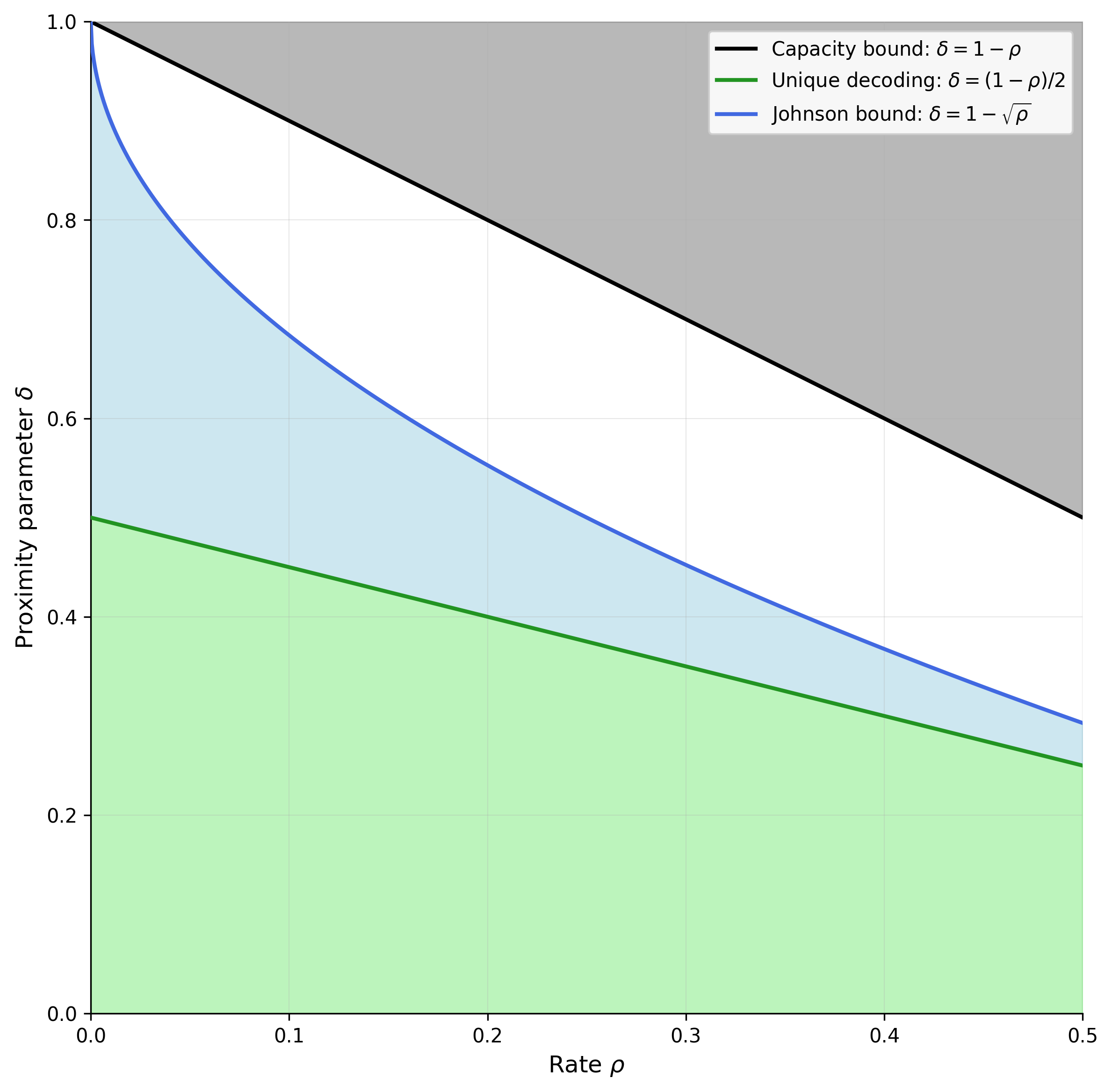
因此,未解决的问题是:“白色区域内会发生什么?”。到目前为止,许多项目都采取了假设白色区域中的参数是安全的方法。这个假设(大致)就是邻近间隙猜想所陈述的内容。
新结果
新的结果部分解决了这个问题,并将其与其他数学问题联系起来。我们将分别讨论这两个方面。
理解白色区域
第一个结果,以不同的形式出现在 DG、CS 和 BCHKS 中,是白色区域中的某些参数选择不安全使用。你可以在下图中看到这一点,其中我绘制了与之前相同的图,但也绘制了 DG 中公式化的新红色区域的近似值。
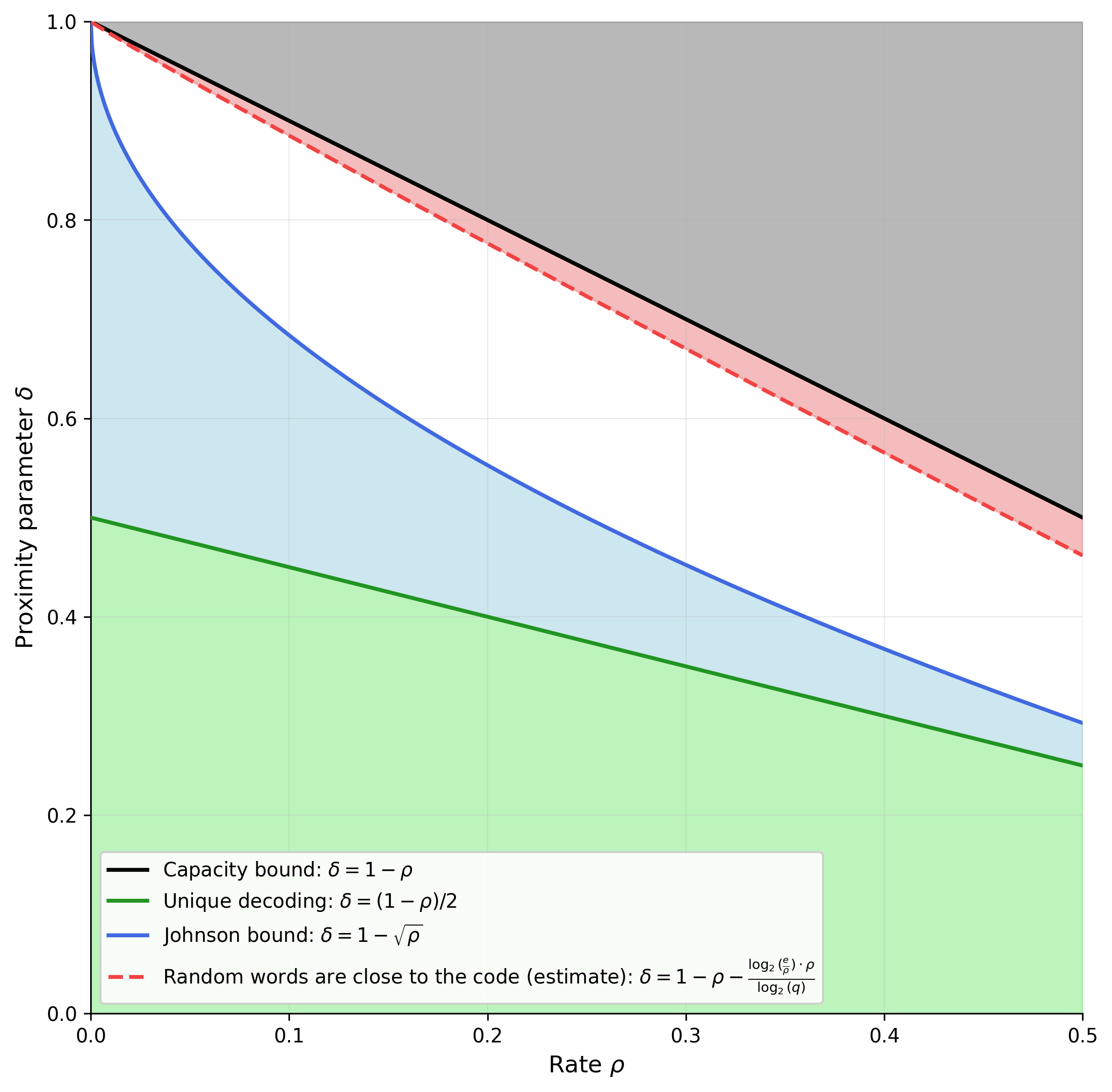
稍后我们将看到这如何影响我们的 SNARKs。在我们这样做之前,让我们讨论一下为白色区域的其余部分所做的进展。
将邻近间隙与其他未解决的问题联系起来
虽然这些论文没有解释整个白色区域的属性,但它们让我们了解了这项任务的难度。CS 和 BCHKS 都表明,判断白色区域的安全性与一个被称为“列表解码”问题一样困难。
粗略地说,这个问题可以表述如下:“如果我通过有噪声的信道发送编码消息,我们可以容忍多少错误,同时仍然能够在另一端恢复小的消息列表?”。这里的小意味着列表大小是消息长度的多项式函数。这是一个未解决的问题。
已知的最佳列表解码算法与图表的蓝色区域完全对应。列表解码也有一个理论上限。我们将此上限覆盖在我们的图表上(参见下面的黄线):
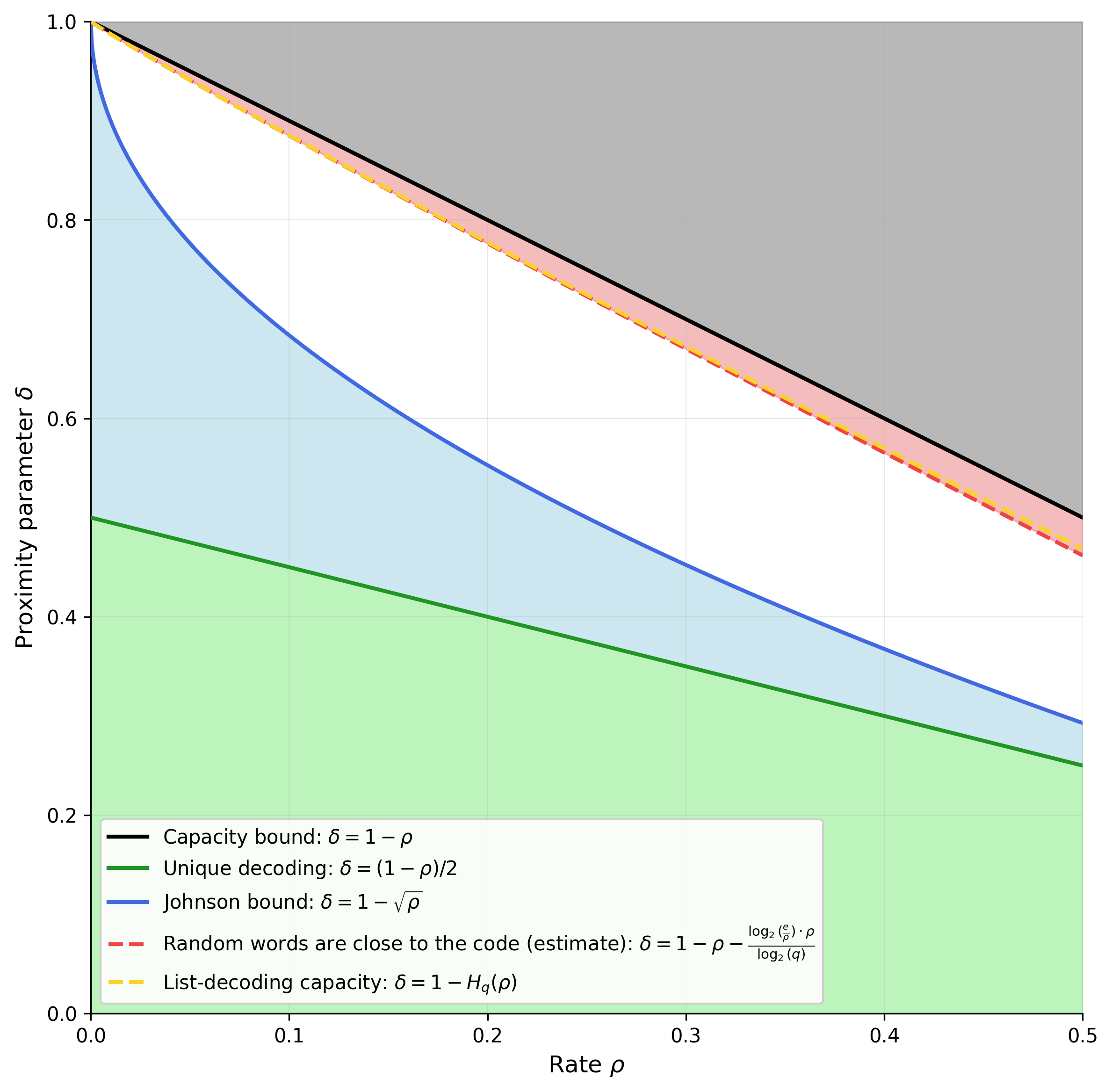
让我强调关于这条新黄线的两个重要事实。首先,也是最重要的一点,它代表了安全参数集的新上限。其次,我们的图表显示它与上一节中的红色区域相交。这不应被视为视觉证据;绘制的红色区域只是 DG 结果的近似值。实际上,我不确定黄色和红色线如何相互作用,特别是因为这两条线都依赖于超出 ρ 和 δ 的参数。
对我们的 SNARKs 的影响
对我们的 SNARKs 的主要影响是我们不能将参数设置为高于黄线或在红色区域中。纠正这个问题需要使用较小的 δ 值并相应地调整邻近测试的其他参数(对于那些熟悉邻近测试的人,我指的是查询的数量)。正如我们所看到的,这意味着证明者时间、验证者时间和证明大小将变得更大。
放大多大取决于选择的新参数:
- 如果我们想绝对安全并在经过验证的安全区域(即,不是白色区域)中运行,则证明大小将加倍。验证者时间也将大致加倍。但是,证明者时间将几乎不受影响!这是因为证明者的计算主要由与 ρ−1 成比例的工作决定,而不是 δ。
- 如果我们想继续在未知的白色区域中运行,那么移动到最接近的可能参数将导致证明大小和验证者时间增加高达 2-3%。与前一种情况一样,证明者时间将几乎不受影响。
结论
最后,我将给你一些关键的要点:
-
基于哈希的 SNARKs 可以在两种参数体系中运行:经过验证的安全性或推测的安全性。前者肯定安全,但性能较差。
-
一些推测的参数被证明是不安全的。
-
仍然存在大片未知的参数区域。
-
调整我们的 SNARKs 以从先前推测的安全性转变为经过验证的安全性会将证明大小和验证者时间增加 2 倍。证明者几乎不受影响。
-
调整我们的 SNARKs 以从先前推测的安全性转变为新推测的安全性会将证明大小和验证者时间增加 2-3%。证明者几乎不受影响。
zkSecurity 为包括零知识证明、MPC、FHE 和共识协议在内的加密系统提供审计、研究和开发服务。
- 原文链接: blog.zksecurity.xyz/post...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 民主事物的再思考:构建共识发现工具 127 浏览
- Zero 链: 技术定位报告 202 浏览
- 以太坊亟需的两大深度改造——二进制树 + VM 改造 237 浏览
- 以太坊 2029 Strawmap 傻瓜指南 278 浏览
- 不实的断言:攻破 6 个 zkVMs 197 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 356 浏览
- 零知识编年史:群 268 浏览
- 以太坊执行层优化:状态树与虚拟机 453 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 304 浏览
- 首次 ZK 攻击发生,且出乎意料 307 浏览
- Vitalik: 以太坊量子抵抗路线图 284 浏览
- zkMesh:2026年2月回顾 363 浏览

