具有缓和发行机制的奖励曲线:EIP研究帖 - 权益证明 / 经济学
- 以太坊中文
- 发布于 2024-04-02 12:26
- 阅读 698
本文提出了一种具有缓和发行机制的奖励曲线,旨在优化以太坊的经济模型。通过调整奖励曲线,可以在保证网络安全的前提下,降低ETH持有者的成本,减少过度质押带来的风险,并鼓励更多人参与到以太坊的生态建设中,维持以太坊的长期健康发展。
具有缓和发行量的奖励曲线:EIP 研究帖子
我撰写此帖子的目的是为了阐述采用具有缓和发行量的奖励曲线的理由。这是即将发布的 EIP 的更长篇幅版本,更详细地介绍了收益和必须权衡的利弊,以及与其他方案的比较。我将尽力回答你在评论中提出的任何问题!
1. 概述
验证者在 The Merge 中开始收到执行层奖励,并且在 Shapella 启用提款后流动性得到改善。这两次升级都有助于增加权益的均衡数量。人们普遍认为,当前的存款规模足以保证以太坊的安全(例如,1, 2, 3)。然而,随着在当前奖励曲线下存入更多的权益,发行量将大幅上升。对于超出安全所需范围的staking的过度激励,不幸的是,随着时间的推移,会变成反常的补贴,带来许多负面影响。这篇文章将探讨缓和发行量的好处和可用的选项。结论是以太坊应该采用候选奖励曲线,该曲线旨在有效控制staking的数量,同时保持可靠的共识激励、经济安全、抵御劝退攻击和卡特尔攻击、良好的staking集合组成以及对单独staking的可行条件。候选奖励曲线将当前奖励曲线的等式除以 1+D/k。然后,单个调整变量 k 用于定义在发行量达到峰值时的staking数量,这也对应于发行量相对于当前奖励曲线减半的点。建议将 k=2^{26} (67.1M ETH) 设置为近期的可行值,随后可能会最终调整为 k=2^{25} (33.6M ETH)。
第 2 节 – 基本原理
提供给staker的均衡收益对应于边际staker分配给staking的成本,即他们在staking和不staking之间的无差异点。第 2.1 节表明,如果以太坊提供的收益高于维持安全性所需的收益,它会迫使用户承担更高的成本,从而降低总体用户效用。这解释了为什么所有 ETH 持有者都可以从减少发行量中受益,如图 2 所示。第 2.2 节回顾了宏观视角。随着权益数量的增长,一个或几个流动性质押代币 (LST) 可能会取代 ETH 成为以太坊中的货币。积极的网络外部性可能导致用户效用降低和协议去中心化。它们的衍生性质也可能削弱社会层维护以太坊预期共识过程的能力。第 2.3 节建议以太坊对拟议的变更采取循序渐进的方法。采取第一个较小的步骤将改善以太坊,而不会造成太大的破坏,可以缓和非均衡状态,并允许对staking组成和数量的影响进行中期评估。
第 3 节 – 拟议的奖励曲线和替代范例
第 3 节介绍了拟议的奖励曲线和替代范例。拟议的奖励曲线标记为选项 A,其发行量随着staking数量超过所需水平而缓慢下降。选项 B 则认为发行量将接近一个渐近最大值。选项 C 是当前的奖励曲线,在整个staking范围内发行量都在上升。第 3.4 节对这些选项进行了比较,展示了奖励曲线如何随着staking数量的增加而发生变化。
第 4 节 – 权衡取舍和先验
第 4.1 节探讨了非池化staker的收益可变性,第 4.2 节回顾了均衡staking收益如何影响单独staker的比例。最大的风险是不利的规模经济使得单独staking变得不太可行。然而,在更高的staking数量下,占主导地位的staking服务提供商 (SSP) 可以提供更低的费用、更好的 LST 货币,以及由于新兴的道德风险而导致的更低的风险。拟议的奖励曲线在整个范围内提供正收益——低到足以使高数量的staking不太可能发生,但又足够高,以至于在更不可能的情况下,永远不会迫使高效设置下的单独staker退出。需要注意的是,关于供给曲线和最大可提取价值 (MEV) 水平的先验与设计相关。第 4.2.3 节分析了在当前 MEV 水平下供给曲线较低的情况,有助于理解拟议的奖励曲线如何帮助共识机制吸收具有低保留收益的委托staker,以确保始终为单独staker提供一些收益。第 4.3 节探讨了staking集合的更广泛组成,强调对委托staking的竞争将在不同的细分市场中进行。鉴于运行一个staking节点的成本相对于收益而言不会变得过高,拟议的变更将允许委托者在偏好和环境中的多样性在塑造staking集合的组成中发挥更核心的作用。第 4.4 节最终绘制了“等比例图”,展示了改变发行政策对staker有利的条件。
第 5 节 – 安全考虑
第 5.1 节讨论了发行政策对短期和长期经济安全的影响。在近期内在整个范围内提供正收益的一个重要原因是,在不更广泛地调整协议的情况下保持共识激励,如第 5.2 节所述。第 5.3-4 节更仔细地研究了劝退攻击和卡特尔攻击。在发行量大幅减少的更严格的奖励曲线下(尤其是在具有负发行量的设计下),这些攻击将变得更有利,因此务必牢记。候选奖励曲线不会实质性地加剧这些攻击的风险。
第 6 节 – 结论和讨论
第 6.1 节总结了不同发行量的优缺点,第 6.2 节介绍了作者的结论,即拟议的候选奖励曲线(选项 A)是以太坊目前最佳的替代方案。选项 C 可以作为临时备份计划。这篇文章最后探讨了未知的结局,扩大了代币持有者的效用衡量标准,以 incorporating 整个生态系统的发展,并告诫不要利用用户对收益的有限理性。
2. 基本原理
2.1 用户效用
将“保留收益”定义为个人愿意进行staking的最低staking收益 y。以太坊的供给曲线由此从潜在的 ETH 持有者的保留收益中产生。图 1 显示了一条假设的供给曲线,该曲线将用于本文的几个示例中。年度总奖励为 Y=yD,其中 D 是staking的数量(“存款规模”)。持有者的保留收益可以描述为“无差异点”,即他们从staking和不staking中获得的效用一样多。因此,供给曲线以下的面积表示staker的隐含总成本 Y_c,而以上的面积表示他们的剩余 Y_s,它们合并为总奖励 Y_c+Y_s=Y。相关成本(广义上定义)包括硬件和其他资源、维护、技术知识的获取、流动性不足、对第三方的信任以及其他增加风险溢价的因素、各种机会成本、税收等。高收益迫使用户承担高于维持安全所需的成本,从而降低了总体用户效用。从“会计角度”来看,slash风险或任何会有效燃烧质押的漏洞不太可能在aggregate协议层面作为纯粹的成本来归因,而且当用户的盈余增加时,税收本质上实际上会增加成本。但是,将供给曲线下方的成本捕捉为不会为staker产生任何盈余的发行的一般原则对于理解staking经济学和福利非常有用。
从当前奖励曲线(黑色显示)到拟议奖励(绿色)的以太坊发行政策的变更,将均衡从黑色方块 (1) 转移到绿色圆圈 (2)。由较深蓝色区域表示的相关成本降低 Y'_c 使所有 ETH 持有者受益,因为 ETH 只是为了抵消staking成本而发行的,而没有产生任何盈余。向均衡的转移还将staker的盈余 Y'_s 转移给所有 ETH 持有者(包括staker)。成本降低由反供给曲线 f(x) 的等式的定积分确定,该积分由比较静态的两个均衡量界定:Y'_c = \int_{_2}^{D_1} f(x)dx\approx 446k ETH。相反,盈余转移被量化为 Y'_s = D_1y_1-D_2y_2-Y'_c \approx 252k ETH。因此,近 2/3 的发行量减少直接有助于福利改善,1/3 将效用从staker重新分配给所有 ETH 持有者。具有相似形状的供给曲线的结果将是相似的定积分和成本/盈余。如果供给曲线在比较静态附近更平坦,则 Y'_c 变得相对更大,而 Y'_s 变得相对更小,反之亦然。
图 1. 使用假设的供给曲线进行staking的隐含成本 Y_c 和剩余 Y_s。发行政策的变更将均衡从黑色方块转移到绿色圆圈。只要协议保持安全和去中心化,成本节省 Y'_c 就会导致aggregate福利改善,而盈余减少 Y'_s 只会将一些效用从staker转移给每个人。
staking收益通常被认为是盈余 Y_s,这意味着发行政策是一个零和游戏。但是,由于staker必须承担的成本,发行政策_绝不是_零和游戏。从根本上理解,通过获得更高的收益,以太坊引导其用户承担更高的aggregate成本。这就是为什么每个人都可以受益在将发行量维持在最低可行水平时,只要他们拥有底层 ETH。
为了说明这一点,所有人所持ETH比例的可实现变化可以计算为
y_p=\frac{1+y}{1+s}-1.
它可以解释为费雪方程式适用于以太坊。可以为staker和非staker计算“比例收益”y_p,在后一种情况下,y=0。流通供给膨胀率 s=i-b 来自于发行率 i=Y_i/S 和燃烧率 b=B/S=0.008,其中 Y_i 是年度发行量,S 是流通供给,B 是年度燃烧量(使用 The Merge 以来的平均值)。light的复合效应,关于对利率的解释的进一步复杂性。图 2 说明了发行量减少对用户效用的假设影响,它比较了两个不同均衡状态下的 y_p。在这里,它显示在拟议的奖励曲线(选项 A)下,并且在之前的工作中展示了在当前奖励曲线(选项 C)下将发行量减半,在稍微不同的供给曲线下。对于比较静态,将 y'_p 从 y^b_p 更改为 y^a_p,将基数效用 u' 的变化定义为
u'=\frac{1+y^a_p}{1+y^b_p}-1,
但在计算 y^a_p 时,对于那些在收益降低时停止staking的人,请使用保留收益作为 y。低于该收益率时,它们无论如何都不会进行staking,因此随着收益率的进一步降低,它们不会遭受额外的效用损失。如下图所示,根据这个定义,destaker将在新的均衡状态下获得更高的效用,而非staker的状况显然更好。以这种方式改善福利的原因是消除了图 1 中蓝色区域的staking成本 Y'_c。当然,从协议的角度来看,单独staker是否继续staking也很重要。这是一个单独的主题,将在第 4.2 节中进一步探讨。该分析仅得出结论,在使用假设的供给曲线的情况下,staker将不受影响(如果他们具有较低的保留收益,则仍然是staker),甚至状况更好(作为destaker)。在第 4.4 节的等比例图中说明了在任何供给曲线下发行政策对staker的影响。
图 2. 使用两个假设均衡状态之间的 y 和 s 的变化来隔离所有代币持有者的基本效用 u' 的变化。Staker受到收益 y 减少的影响,但通货膨胀率 s 的降低相似,因此他们不受影响(y_p 保持不变)。一旦 y 跌破其保留收益,De-staker就不会遭受进一步的效用损失。他们与非staker一起从 s 的降低中受益。
Schwarz-Shilling 和 Dietrich 将 y_p 称为“真实总staking收益”(他们未在其帖子中指定方程式,但可能暗示着他们使用 y_p=y-s;为了视觉清晰起见,b=0)。他们跨奖励曲线的绘图,包括选项 A 的绘图,对于概念化度量本身非常有用。
2.2 宏观视角
奖励曲线会影响所有流通 ETH 中进行质押的比例,因此重要的是要检查以太坊发行政策的宏观视角](https://notes.ethereum.org/@anderselowsson/MinimumViableIssuance#Benefits-of-MVI-from-a-macro-perspective)。这可以被视为[真实成本核算](https://en.wikipedia.org/wiki/True_cost_accounting)的一个组成部分,将第 2.1 节扩展到纳入外部性。
LST 超过对其控制下的staking比例的关键阈值可以获得超额利润。这种区块空间的卡特尔阶层最终可以损害共识机制。如果广泛的发行政策(当前的奖励曲线可以说是代表了这一点)使 LST 能够控制总 ETH 的很大一部分(受货币功能的网络外部性推动),那么以太坊的风险会进一步加剧。然后,受损的机构位于共识机制之上一层,即社会层。随着The DAO的出现,很明显,如果受结果影响的流通供给总额的比例增长到足够大,那么“社会层”可能会动摇其对底层预期共识过程的承诺。如果社区不再能够有效地干预例如 51% 的活跃度攻击,那么 Buterin 讨论的以警告系统形式出现的风险缓解可能无效。在这种情况下,股权证明共识机制通过衍生工具与以太坊用户之间的联系如此紧密,以至于它已经超载了其最终仲裁者,即社会共识机制。这是一个特殊且以某种方式倒置的问题,Buterin先前警告过。
如果发行政策导致所有 ETH 的很大一部分被质押,那么一个或几个 LST 可能会在以太坊生态系统中超越作为货币,并将其嵌入到每一层和应用程序中。正如已经指出的那样,这是某些 SSP 的刻意目标。通过缓和发行,每个 LST 将与非质押 ETH 进行更激烈的竞争,从而确保生态系统中的不可信任资产。社会层不会与外部组织及其发行的 ETH 衍生品共同依赖。然后,可以将委托stake给占主导地位的 LST 的委托-代理问题 (PAP) 更准确地定价,因为道德风险的可能性较小。在以太坊社会层眼中,没有 LST 会变得“太大而不能倒闭”。这种定价将反映出,代表委托人行事的代理人(或任何能够将自己插入到该关系中的一方)获得了更大的机会来降低共识以获取自己的利润,而它控制的stake比例越大。然后,委托质押者必须不断评估其安全保障(例如,质押代理人或插入方的自身风险价值),因为他们知道如果最坏的情况发生,他们可能会失去一切。
2.1 节中探讨的一项成本也可能在宏观层面影响以太坊。在每个人都必须质押以避免看到他们的储蓄被侵蚀的情况下,不同辖区之间的税收政策差异可能会阻碍地理去中心化。
2.3 循序渐进的方法
有一些支持循序渐进的方法的论点,即在一个硬分叉中朝着正确的方向迈出一小步,评估结果,并在适当情况下采取最终步骤:
- 损害经济主体提前计划的能力会降低福利。虽然早在 2021 年就开始出现一些旨在缓和发行的提案(1, 2, 3),但不能期望单个单独的质押者过于密切地关注研究辩论。他们可能会在做出决定或认真考虑后才开始关注。信号要缓和意愿的意思是缓和发行量,但是缓和发行量和已经做出的真实决定之间也存在差异。在做出决定后相对较短的时间内实施对发行政策的更改时,循序渐进的方法特别有吸引力。与此同时,在这一点上,进行股权质押的数量已经超过了提供足够安全性的水平。在这一领域,进一步的增长必须被视为会降低福利。在这种情况下,循序渐进的方法可以:
- 为单独的质押者以及 SSP 提供更长和更循序渐进的适应阶段。
- 在短期内采取措施来缓和进行股权质押的激励,同时又不会造成太大的破坏。
- 向可能没有密切关注正在进行的讨论的用户传达进行额外调整的可能性。
- 忽略进行股权质押的决策中的摩擦,减少发行量将导致一个临时阶段,其收益低于均衡水平,直到一些质押者离开并建立新的均衡。循序渐进的减少可以缓解此问题。更循序渐进的减少,例如,对每个 epoch 的发行量进行小幅调整,将带来更多的实施开销。
- 目前尚无法确定是否需要完全减少发行量,才能缓和质押数量的增长 - 这仅仅是一个合理的估计,取决于对进行股权质押的决策中的摩擦或供给曲线下降的假设。因此,至少作为对这些不确定因素的确认,逐步行动似乎是明智的。考虑到该推理MEV 的计划即将到来,这也会影响股权质押收益(如果实施)。
- 有关发行水平的几个属性,如特别值得关注的,例如保留的单独的质押者的比例。循序渐进的方法使评估中间结果成为可能,然后再实施完全设想的发行量减少。即使研究人员确信完全减少可以使相关属性保持平衡,但中途评估之后的循序渐进的方法会使那些可能反对的人更容易接受更改。
下一节将介绍奖励曲线,该曲线合并了作为循序渐进的方法一部分的潜在中间步骤。
3. 建议的奖励曲线和替代范例
在当前情况下,可以根据三种基本范例来设计奖励曲线(例如,不存在 MEV 燃烧,没有股权质押费用,并且希望控制收益变异性;另请参见第 4.1 和 5.2 节)。这些已在先前工作的表 2中作了规定,在此处总结在表 1 中。选项 A 是建议的奖励曲线。正如第 2.1-2.2 节倡导的那样,它最适合改善用户效用和缓和质押数量。选项 C 在几乎所有人进行质押的情况下,为(单独)股权质押提供更高的收益。当然,这也可能被视为一个缺点,即在第 4.1-4.3 节中进一步研究的一个折衷。选项 B 在这两种方法之间进行平衡。第 3.4 节将绘制在一起的奖励曲线,以便进一步比较,包括完全减少和循序渐进的方法。
| 发行量 | 好处 | |
|---|---|---|
| 选项 A: | 在高于充分安全性的存款规模时略有下降。 | 改善用户效用并缓和质押数量。 |
| 选项 B: | 渐近线接近最大固定水平。 | 平衡选项 A 和 C 的好处。 |
| 选项 C: | 继续无限期地增加。 | 如果质押数量接近最大值,则为单独股权质押提供更高的收益 |
表 1. 奖励曲线的三个主要类别,在本节中逐一进行探讨。选项 A 是作者首选的建议方法。
3.1 选项 A - 建议的奖励曲线
概述
建议的奖励曲线会衰减超出足以确保安全性的质押数量之外的发行量。它的设计目标是提供非常清晰的心理模型:单个调整变量 k 的值还定义了峰值发行量和发行量减半点(相对于当前奖励曲线)处的质押数量。在之前一篇关于发行量属性的文章中,该奖励曲线被展示为候选奖励曲线。图 3 说明了在验证器性能完美的情况下,跨存款规模的年度发行量水平。黑色当前奖励曲线的发行量根据公式 Y_i=cF\sqrt{D} 随存款规模变化,其中 F 设置为 64,常数 c\approx2.6。灰色曲线显示发行量减半(F=32)。绿色建议的奖励曲线引入了除以 1+D/k
Y_i=\frac{cF\sqrt{D}}{1+D/k},
其中 c 和 F 保持不变。完全减少的目的是 k=2^{25},这使得在 2^{25}(33.6M)ETH 质押处的峰值发行量略低于 0.5M ETH(加号),这也是减半点。虚线绿色曲线 k=2^{26}(约为 67.1M) 指示循序渐进的方法中的一个潜在步骤。奖励曲线规定了最大发行量级别这一事实可能从沟通角度来看是有益的。将来,以太坊的奖励曲线将转换为随存款比率 d=D/S 变化(参见第 6.3 节),这将转换为最大流通供应通货膨胀率。
图 3. 绿色建议的奖励曲线 - 选项 A - 的发行量水平,与黑色当前奖励曲线相比。虚线绿色线表示循序渐进的方法中逐步减少。相对于当前奖励曲线的减半的发行量用灰色和加号表示,加号表示减半点和发行量峰值。
图 4 说明了绿色股权质押收益,假设已实现的提取价值 (REV) 为 V=300k ETH/年 (REV 是构建者扣除费用后的 MEV,当前的通行费略高于 30 万)。股权质押收益的公式为 y=y_i+y_v,其中 y_i=Y_i/D,y_v=V/D。因此,发行收益的公式变为
y_i=\frac{cF}{\sqrt{D}(1+D/k)},
再次将当前奖励曲线(y_i=cF/\sqrt{D})的分母乘以 1+D/k。与第 2.1 节中相同的假设供给曲线包含在图 4 中。它用于说明现在起几年内供给股权质押的倾向可能会在收益和存款规模之间发生变化,以及改变后的奖励曲线会对股权质押均衡产生什么影响。在此特定示例中,均衡收益率降低了 0.6%(约 1/5),从当前奖励曲线的 2.94%(黑色矩形)降至新奖励曲线的 2.34%(绿色圆圈)。在循序渐进的方法中,均衡收益率仅降低了 0.43%(约 1/7)。
一个合理的假设是,随着股权质押体验简化和 DeFi 集成改进,供给曲线将随着时间的推移逐渐向下移动。这实质上将取决于第 2.1 节中概述的各种成本如何演变。淡蓝色曲线可能是再过一两年后的供给曲线。这将进一步降低当前和新奖励曲线下的收益。在某些情况下,供给曲线也可能会向上移动,例如,由于共识失败促使股权质押者重新评估风险,或者由于对非股权质押 ETH 的需求增加而导致机会成本升高。
图 4. 绿色建议的奖励曲线 - 选项 A - 的质押收益(包括 REV),与黑色当前奖励曲线相比。虚线绿色描绘了循序渐进的方法。从黑色方块到绿色圆圈的假设均衡变化表示为指导原则,但由于关于供给曲线和未来 REV 水平的不确定性,该变化仍然具有推测性。
奖励可变性
在为 EIP 准备的过程中,使用当前 REV 数据执行了奖励可变性的仿真。图 5 显示了建议的奖励曲线在其完整实施中,在各种存款规模下,单独的质押者的模拟累积分布函数 (CDF)。图 6 而是显示了循序渐进的方法的模拟结果。
图 5. 在候选奖励曲线和当前 REV 水平下,各种质押数量下单独的质押者收益可变性。预期的抵押收益以虚线垂直线表示。
图 6. 在候选奖励曲线的循序渐进式实施和当前 REV 水平下,各种质押数量下单独的质押者收益可变性。预期的抵押收益以虚线垂直线表示。
3.2 选项 B - 渐近线固定发行量
概述
一个较为温和的选择是改为将当前奖励曲线除以 1+\sqrt{D}/k,从而得出发行量
Y_i=\frac{cF\sqrt{D}}{1+\sqrt{D}/k}=\frac{cF}{D^{-0.5}+k^{-1}}.
该公式本质上是对数逻辑 CDF,因此发行量将接近渐近线最大值 cFk(但在以太坊以其当前流通供应量运行时可能不会接近该值)。图 7 以橙色说明了选项 B 的潜在奖励曲线,其中 k=2^{12},而潜在的循序渐进方法中 k=2^{13}。如此图中所示,调整了变量 F,以便在特定级别产生与选项 A(和选项 C)相似的发行量,以便于在后续部分中进行比较。因此,以加号标记的减半点也在 D=2^{25} 附近,并且循序渐进的方法在当前质押数量 (31M ETH) 下与选项 A 的发行量相匹配。但是,可以重新调整 F 为 64,这将增加在较低质押数量下达到均衡的概率。
图 7. 相对于黑色当前奖励曲线,橙色选项 B 的发行量水平。虚线橙色线概述了潜在的循序渐进方法中的逐步减少。相对于当前奖励曲线的减半的发行量以灰色和加号表示。
发行收益的公式改为$y_i=\frac{cF}{\sqrt{D}+D/k}$.
它与其他的奖励曲线一起绘制在第 3.4 节的图 10 中。
3.3 方案 C – 降低基本奖励因子的当前奖励曲线
概述
最简单的方案是降低基本奖励因子,保持当前的奖励曲线。完整的降低幅度可以是 F=32。值得注意的是,这种奖励曲线会相对更多地降低较低质押量的收益,因此从安全的角度来看,F 很难降低到 32 以下,至少目前是这样(另见第 5.1 节)。一个渐进的方法应该选择 40-48 之间的范围。在这篇文章中,将以 F=44 为例进行说明,因为渐变的奖励曲线将与其他所有曲线重合,以便于比较。图 8 绘制了发行量。收益率与其他的奖励曲线一起绘制在第 3.4 节的图 10 中。
图 8. 方案 C 的发行量水平,依赖于降低基本奖励因子的当前奖励曲线。虚线灰色曲线表示渐进方法的一种潜在设置。在保持足够经济安全性的前提下,完全可能的降低幅度是发行量减半,如灰色曲线所示。
3.4 方案 A-C 的比较
图 9 显示了三种概述的方案,包括完全降低和渐进方法。在完全降低的情况下,所有曲线在 D=2^{25} ETH 附近重合(圆圈),在这一点以上,方案 A 的发行量下降,方案 B 的发行量趋于平稳,方案 C 的发行量继续增加。在渐进方法中,所有曲线(虚线)在当前 31M ETH 的质押量(星形)附近重合,之后它们以类似的模式发散。值得注意的是,如果所有 ETH 都被质押,则方案 A 和(略微地)方案 B 的渐进方法给出的发行量低于方案 C 的完全降低。
图 9. 方案 A-C 的发行量水平比较,其中渐进方法用虚线表示。对于完全降低(圆圈),这三个方案在质押量约为 2^{25} ETH 时提供相同的发行量;对于渐进步骤(星形),则在 31M ETH 时提供相同的发行量。在这一点以上,方案 A 的发行量下降,方案 B 的发行量趋于平稳,方案 C 的发行量继续增加。
图 10 显示了相同三个方案的质押收益率(按目前的 REV 水平)。黑色双向箭头表示,在目前的质押量下,质押收益率的初始降低将低于 1 %。蓝色双向箭头捕捉了先前相同假设供给曲线下的收益率均衡变化,表明在第一个渐进步骤中,假设的收益率降低将低于 0.5 %。
图 10. 方案 A-C 的质押收益率比较(按目前的 REV 水平),其中渐进方法用虚线表示,当前奖励曲线用黑色表示。图中指示了从黑色方块到圆圈的均衡变化作为指导,但供给曲线和未来的 REV 都存在不确定性。渐进方法的初始降低低于 1 %(黑色箭头),在假设的均衡状态下低于 0.5 %(蓝色箭头)。
4. 权衡和先验
4.1 单独质押者的可变性
如果发行量受到调节,则奖励的较大部分将来自 REV,因此质押奖励的相对可变性将增加。这对单独质押者产生负面影响,因为他们无法轻松地依靠资金池来平滑可变性。使用当前的 REV 数据对奖励可变性进行了模拟,得出了例如图 5-6 的 累积分布函数,以及跨越 y 和 D 的年化收益率的标准差(SDs)映射。认识到质押者可能对 较低质押收益率的方差更敏感,因此标准差除以预期收益率的平方根,称为 SSD。此衡量标准旨在捕捉非资金池质押者的可变性退化。图 11 绘制了本研究中不同奖励曲线的 SSD 随质押量的变化(越低越好)。显然,随着质押量的增加,方案 A 的 SSD 将略有上升。考虑到牺牲一些可变性来降低质押量是合理的,因此这种增加被认为是可接受的。当单独考虑时,甚至可能希望 SSD 在较高的质押量下比在较低的质押量下稍微差一些。但是,在任何 D 下具有较低的 SSD 当然是更可取的。
图 11. 不同奖励曲线的 SSD(越低越好)随存款规模的变化。
4.2 均衡收益率和单独质押者的比例
4.2.1 概述
以太坊希望保留单独质押者,至少在衡量所有质押者的比例时是这样。降低发行量水平的预期结果是,与不降低发行量相比,委托质押者和单独质押者质押的 ETH 将更少(1, 2)。以图 10 为例,尚不清楚在质押量约为 33M ETH 且质押收益率为 2.34 % 的假设均衡状态下,单独质押者的比例是否低于在质押量约为 50M ETH 且质押收益率为 2.94 % 的状态下。人们担心的是,由于与单独质押相关的固定成本相对较高,因此可能存在一个质押收益率,低于该收益率,尤其是一些单独质押者会放弃质押。如果单独质押者在收益率低于 2.5 % 时大量退出,那么在质押量为 33M ETH 时的 2.34 % 的质押收益率将比在质押量为 50M ETH 时的 2.94 % 的收益率给出更低的比例。这当然是需要认真对待的事情。规模经济很难在去中心化的区块链中被设计掉。
但是,也有一些论点说明,更严格的奖励曲线可能会给出更高或至少相似的单独质押者比例(另见第 2.2 节):
- 占主导地位的 共享安全池 (SSPs) 在 更高的质押量下具有更好的规模经济,从而增加了他们在单独质押者中的成本优势。
- 同样,货币功能的积极网络外部性 随着质押量的增加而增长,并且随着主导的 LST 发行 SSP 的竞争优势而增长。
- 此外,如果其他所有人都使用 LST,那么与 LST 相关的 协议抽象支付 (PAP) 风险可能看起来更低,并期望社会层会在发生故障时对其对预期共识过程的承诺动摇。
- 随着收益率的下降,风险很可能会比单独质押者更早地将委托质押者排除在外。如果很大一部分潜在的委托者认为他们希望持有的 LST 在一年内有 1 % 的失败风险,那么有利的规模经济或流动性可能不足以作为竞争优势。自我托管无疑对相当比例ETH 代币持有者来说 有重要意义;在评估质押供给侧时不应忽视这一因素。
- 拥有足够 ETH 和进行单独质押的技术能力的代币持有者不一定 बहुत 多,这意味着单独质押量的 软上限。可以认为,如果这个池或多或少地耗尽了,那么在当前政策下,随着供给曲线下降且 D 增加,新的质押者 中相对 [很少一部分] 将成为单独质押者。尽管如此,关于这个特定的论点,应该记住的是,如果大幅降低收益率以阻止 D 增加,则不能保证长期内会保留更大比例的单独质押者。这最终取决于它们之间预留收益的更精细分布。
发行政策应侧重于长期目标,而不应依赖短期补救措施。这还与目前相当有价值的单独质押 空投 有关,如果可以预期它们会停止。然而,以太坊不断发展的共识机制可能在十年后看起来有所不同,对质押有不同的要求——甚至可能存在不同类别的验证者(1, 2)——因此,当前和近期未来的情况不能完全被忽视。第四个要点还可以添加一个额外的细微差别:一些单独质押者质押的 ETH 远远超过 32 ETH,并且这些人可能最能抵御低收益率。最后请注意,不拥有自己硬件的单独质押者仍然可以享受一些外部规模经济;相反,家庭质押者直接受到硬件成本的影响。
从根本上讲,推测是 不同类别的质押者之间预留收益的相对分布可能不同。然后,这导致在不同发行政策下单独质押者的比例不同。但是,在这种情况下,一种政策是否优于另一种政策无法确定,并且在未来十年内也可能有所不同。这个研究主题肯定会受到进一步关注(1, 2)。
4.2.2 关于供给曲线和 REV 的先验
研究图 5 中方案 A 的质押收益率 累积分布函数 中 1.1 亿 ETH 的质押量所提供的收益率可能会引起特别的关注。那里的预期质押收益率仅为 0.65 %。在代币价格约为 3000 美元的情况下,32 ETH 的质押仅能产生略高于 50 美元的预期月收入。并非来自区块提议或 同步委员会 职责的“保证的”证明收益率仅为该收益率的一半。ETH 代币价格的下降可能会进一步减少质押收入。但是,应该注意的是,对于供给曲线的一个合理的先验是,对于质押的 1.1 亿 ETH 来说,收益率必须远高于 0.65 %。只有当 REV 显着增加时,才能预期在质押的 1.1 亿 ETH 处达到均衡,从而将质押收益率提高到所需水平。因此,在高质押量下降低发行收益率的一个容易被忽视的好处是,它可以抢先应对更高的 REV(在均衡状态下,质押收益率永远不会低于边际质押者的预留收益率)。当然,也可能有人担心允许质押量首先扩展到 1.1 亿 ETH 这一事实,因为已经有很好的论据反对这样做。为什么要提供任何收益率?除了关心单独质押者之外,第 5.2 节还提供了目前与共识激励相关的重要原因。
4.2.3 低收益率情景
虽然在拟议的奖励曲线(方案 A)下,高质押量很可能与 REV 的较高水平相关联,从而保持略微更高的质押收益率,但检查替代情景仍然很有价值。如果供给曲线确实在未来十年内大幅下降到非常低的水平会怎样?在目前的 REV 水平下,方案 A 在质押的约 7460 万 ETH 时给出的质押收益率为 1 %。方案 B 在那里给出的质押收益率为 1.16 %,方案 C 将其设置为 1.37 %。但是,对于方案 B 和 C,均衡当然会转移到更高的质押量,从而在此过程中略微降低收益率。在方案 A 的均衡收益率为 1 % 的情景下,方案 A-C 的假设结果(绿色圆圈)如图 12 所示。当然,推测在这种不太可能的情景下供给曲线会是什么样子具有挑战性,但是绘制一种可能的结果以帮助理解可能仍然很有帮助(它与 先前研究 中一样,使用 k=1 且 c_2 = 0.001 形成)。然后,方案 B 在约 8000 万 ETH 的均衡状态下给出的收益率为 1.09 %(橙色圆圈),方案 C 在约 8700 万 ETH 的均衡状态下给出的收益率为 1.24 %(灰色圆圈)。哪种结果对以太坊更好?
图 12. 在低供给曲线的情景下,假设的均衡状态,该曲线在当前 REV 水平下与方案 A 的 1 % 质押收益率相交。
如果许多单独质押者的预留收益率在 1.24 % 和 1 % 之间——在这个特定情景中,大多数人的质押预留收益率低于 1 %——那么他们可能会不成比例地更容易放弃。这回到了单独质押者的相对较高固定成本与高质押量下 LST 的优势之间的权衡:主导的 SSP 可以提供更低的费用、更好的 LST 货币以及由于新兴的道德风险而降低风险的概念。
可以设计以太坊以强制执行供给曲线上任何点的均衡(但必须 关注 y_i 相对于 y_v 的水平)。在这种供给曲线下,强制执行蓝色星形处的均衡是否更可取?它对应于质押的 3000 万 ETH 和约 0.37 % 的总质押收益率。目前,在质押的 3000 万 ETH 时,y_v 为 1 %,因此需要引入质押费并每个 世代 都收取。这将需要让单独质押者 每个世代都赔钱,因为他们有机会被分配提议一个区块。这个结果相当没有吸引力。但是在引入 MEV 销毁 之后呢,那时是否可取?有几个论点支持它(例如,第 2 节),但由于相对较高的固定成本,它也可能使单独质押相当不利。以这种方式在这一点强制执行少量质押时,质押集的 组成 更难预测(也请参阅下一小节)。如果在质押的 3000 万 ETH 时均衡收益率为 2.6 %,就像候选奖励曲线一样,那么结果的争议性要小得多。从蓝色星形到绿色圆圈的均衡质押量的向上转变 充当“安全阀”,这有助于以太坊抵消在较低供给曲线下少量质押的不太理想的特性。共识机制基本上吸收了所有具有低预留收益率的委托质押者,只是为了将收益率提高到足以让单独质押者仍然以 32 ETH 验证器获利。无论这是否可取,为了用户的缘故,只有在绝对必要时,才必须发生向上转变。奖励曲线有助于实现这一点。
有趣的是,还要注意在这种假设的供给曲线下,拟议的方案 A 和当前奖励曲线之间的差异。图 12 中黑色方块处的质押收益率约为 2 %,因此质押的激励要高得多,从而吸引了 1.05 亿 ETH 进入质押。缺点与之前讨论的相同。每个人都被迫质押以避免他们的储蓄被侵蚀。黑色方块处的发行量约为每年 170.8 万 ETH,即几乎是方案 A 下的四倍。因此,即使收益率增加了近 1 %,供给通货膨胀率增加的幅度甚至更大。因此,值得注意的是,在当前奖励曲线下,质押者的处境仍然比方案 A 更糟,并且每个人都在 u' 方面遭受损失。这是因为 y_i 的收益不会在实质上超过发行率增加的损失 i=y_id,其中 d 是存款比率 d=D/S。因此,要使发行量增加在高存款比率下有利可图,供给曲线必须几乎垂直向上倾斜,如第 4.4 节和图 14 中进一步探讨的那样。
在图 12 中具有低供给曲线的示例中,从方案 C(灰色圆圈)更改为方案 A(绿色圆圈)可将发行量减少约 33 万 ETH,从约 77.5 万 ETH 降至 44.6 万 ETH。大约 42 % 的减少量对应于隐含成本 Y'_c 的降低。ETH 持有者的效用变化如图 13 所示。每个人在方案 A 的均衡状态下都比方案 C(不考虑摩擦)更好。但是,如前所述,这并不意味着单独质押者会继续质押。如果他们的预留收益率介于 1 % 和 1.24 % 之间,他们甚至可以通过取消质押来获得更好的收益。从宏观角度来看,如果单独质押者的比例下降太多,那么整个协议(包括 ETH 代币持有者)可能会变得更糟。宏观视角与第 6.4 节中的用户效用进一步交织在一起。
图 13. 在低供给曲线下进行从方案 C 更改为方案 A 时,隔离效用 u' 的变化。质押者受到收益率 y 降低的影响,但通货膨胀率 s 的降低幅度更大,因此他们的收益略好。一旦 y 降至其预留收益率以下,取消质押者就不会遭受进一步的效用损失。他们与非质押者一起从 s 的降低中受益。
4.3 均衡收益率和质押集的更广泛组成
发行量水平与 SSP 多样性之间的关系也需要在规模经济与诸如货币功能的积极网络外部性等因素之间进行 权衡。在整个质押范围内提供正收益率有助于减轻人们的担忧,即具有结构性优势的主要 SSP( 如 中心化交易所 (CEX))——可能利用一些假设的质押 ETF——可以将他们的质押比例提高到关键水平。与此同时,不应过度强调围绕此类实体的中心化风险,而忽略其他风险情景。如今,已经有一些 SSP 通过利用链上网络外部性来获得关键的质押比例,表面上放弃利润以追求垄断。这种类型的结构性优势随着更高的发行量而增长,并且在原生 ETH 相对于一种 LST 可能占少数之前扼杀它,必须被认为是社区的净收益。在权衡这些权衡时,一种不可避免地迫使任何结果(无论是极低还是极高的质押量)发生的发行量水平似乎并不可取。正如在讨论单独质押时一样,如果供给曲线确实非常低,那么似乎可以接受让存款规模增长到略高于足以确保安全的水平,以便仍然存在一些质押收益。如果事实证明供给曲线相当高,那么低存款规模是完全可以的。如果在 2.6 % 的质押收益率和 3000 万 ETH 的质押量下达到均衡,那么没有哪个 SSP 可以合理地击败所有其他 SSP(如方案 A)。
除了运行质押节点的成本外,每个 SSP 在寻求特定细分市场时都会产生独特的成本,其范围从合规性到软件不等。事实上,CEX 在某种程度上对他们的客户即委托者拥有本地垄断,并且使费用与任何链上选项保持竞争力的机会成本可能非常高,以至于它不代表利润最大化策略。很明显,对委托质押的竞争将在不同的细分市场中展开,并且完全竞争不是一个合理的假设。鉴于相对于收益率而言,运营节点的成本不会被设定得过高,因此拟议的奖励曲线(或任何其他选项)不会明确强制执行低质押量,最终允许委托者之间在偏好和情况方面的差异在塑造质押集的组成方面发挥更核心的作用。因此,没有令人信服的论点说明在方案 A、B 或 C 下任何一个 SSP 将超越其他 SSP。当采用渐进的方法并在继续之前评估结果时,这一点尤其重要。在这种情况下,在当前奖励曲线下已经更有可能出现中心化风险,其杠杆作用是某种新兴的主导 LST 作为以太坊的货币。
4.4 等比例图
图 14 绘制了先前指定销毁率 b=0.008 和年度 REV V= 30 万 ETH 下横跨 y 和 D 的质押者的 y_p。细黑线可以描述为横跨 y_p 保持恒定的“等比例”线(参见下面的等式)。对于试图了解发行政策对其流通供应份额的影响的质押者来说,等比例图至关重要。如果在某个特定均衡状态下,供给曲线的斜率比相关的等比例线更陡峭,则质押者将受益于发行量的增加(u'>0);如果斜率更平缓,则他们的处境会更糟。在微观经济学中,“生产可能性曲线”可以与等利润线进行比较,以优化生产集。对于质押者来说,供给曲线变成了“比例可能性曲线”(质押经济学的 PPC),它捕获了质押者可获得的流通供应比例如何随发行政策而变化。
图中用蓝色显示了两条假设的供给曲线,一条是来自图 12 的低供给曲线(虚线),另一条是来自先前图的基准供给曲线(实线)。紫色等比例线与当前奖励曲线的均衡状态(正方形)相交。由于供给曲线(PPC)在均衡状态下的斜率更平缓,因此质押者不会从发行量增加中受益,因此在这两种情况下都会从发行量减少中受益。在拟议奖励曲线的均衡状态下,他们的处境显然更好(更高的 y_p),并且在基准供给曲线下保持漠不关心(如图 2 所示)。星形标记供给曲线达到其最大 y_p 的位置,切线与相应的等比例线。对于质押者来说,这是 y_p 方面的理想均衡。所有其他代币持有者当然仍然会从发行量减少中受益,因此就 u' 而言,他们肯定更喜欢在低供给曲线下在质押的 2000 万 ETH 处达到均衡(三角形),在这种情况下,质押者的处境与最初的水平一样好。
图 14. 等比例图,说明了在均衡状态下图发行政策对质押者比例收益率 y_p 的影响。由于紫色等比例线在均衡状态下具有更陡峭的斜率,因此在两种假设供给曲线下,从当前奖励曲线(黑色)减少发行量对质押者来说是有利可图的。星形表示沿供给曲线可获得的最大 y_p。
将 v 定义为 REV 率 v=V/S。然后,任何特定 y_p 的等比例线遵循等式
y = \frac{y_p-(1+y_p)(v+b)}{1-d-y_pd},\quad \quad y_p<\frac{1-d}{d}.
这个等式暗示了可以在任何均衡状态下施加在供给曲线下的盈利能力的基本条件(例如,通过弹性推导和分析)。如果(反)供给曲线遵循该等式(沿任何指定的 y_p),那么质押者将对整个存款比率范围内的发行量变化无动于衷。
5. 安全考虑因素
5.1 经济安全
在推理以太坊的经济安全性时,需要注意某些关键阈值。持有超过 1/3 的质押量的攻击者可以延迟 最终确定性,持有超过 1/2 的攻击者可以控制 分叉选择,持有 超过 2/3 的质押量的攻击者可以最终确定链。这些攻击中的每一种都会造成严重的破坏,但对攻击者来说,潜在的成本很高。在延迟最终确定性的情况下,攻击者会受到 不活跃泄漏。在某些特定的时间内以某些特定的方式导致最终确定性损失的成本,与总存款规模成线性关系,并且与时间成 二次关系。在不活跃泄漏期间,离线验证者会在不到三周的时间内泄漏大约一半的 ETH。导致最终确定性损失(和其他攻击)的完整成本分析还需要考虑攻击者必须控制的 ETH 的价格波动。攻击者可能会损失 ETH,并且看到他们仍然保留的任何 ETH 的价值减少——如果攻击对以太坊造成真正的损害。对于通过持有超过 1/2 或 2/3 的质押量而发动的攻击,很自然地假设 社会层会进行干预。最终的追索权是将攻击者的部分或全部质押量销毁。
当谈到来自较小质押量的攻击时,有 几次重组攻击 和少数人劝阻攻击(第 5.3 节)需要考虑。这些攻击中的许多攻击还取决于攻击者持有的质押比例(即,持有 25 % 的质押量比持有 0.1 % 的质押量开辟了更多的途径)。从这个简短的综述中,很明显,质押量不能太小,因为对以太坊造成严重破坏的成本与造成的损害不符。表 2 表示在 $3000 的代币价格下,在存款规模为 1400 万 ETH(合并时的存款规模)、2400 万 ETH(20 % 的质押量) 和 3000 万 ETH(接近当前的存款规模)时的 1/3、1/2 和 2/3 的质押量的成本。
| 1/3 | 1/2 | 2/3 | |
|---|---|---|---|
| 14M | $14B | $21B | $28B |
| 24M | $24B | $36B | $48B |
| 30M | $30B | $45B | $60B |
表 2. 在几个相关的存款规模下,在 $3000 的代币价格下,关键比例 1/3、1/2 和 2/3 的质押量的风险价值。
虽然回顾一下各种存款规模下潜在攻击的当前 法定货币 计价成本令人感兴趣,但在长期来看,以太坊的经济安全将内在的与 ETH 保持其价值的能力联系起来。因此,在考虑经济安全时,采取全面的观点也很重要。通过反思以太坊的早期,当时 ETH 代币的价值要低得多,就可以突出这一点。八年前,在 2016 年 5 月,Buterin 思考了 以太坊可以在存款比率 d=0.3 下保护和无法保护的价值。当时,ETH 代币的市值约为今天的 500 倍,因此以太坊可以提供的经济安全性受到限制。将存款比率从 0.3 提高到 0.6 只能将 1/3 的质押量从 7000 万美元增加到 1.4 亿美元。这突出表明,一旦存款比率上升到微不足道的水平以上,最终将决定以太坊经济安全的是以太坊在世界经济中的作用以及以太坊在以太坊经济中的作用。因此,必须考虑本文所有部分(包括即将到来的第 6.4 节)的见解,才能确定合适的存款比率。这是一项无法客观地正式化的复杂任务。请特别注意,质押收益率的水平(当单独考虑时)不会成为 ETH 代币价值的决定因素,因此以太坊的经济安全性也将不会受到影响,因为收益率来自新铸造的代币,直接稀释了持有者。 到了某个时候,增加另一个验证者的边际安全收益所带来的效用,低于先前概述的过度发行所带来的众多不利因素造成的效用损失。这一点暗示了一个理想的存款比率。Justin Drake 在 Reddit 上最近的 AMA 中建议 d=0.25 (30M ETH) 是合适的。Vitalik Buterin 也表示同意,并详细阐述了沿着第 4.3 节的思路影响 staking 集合的更广泛组成的因素,但也补充了一个个人观点,认为 d=0.125 (15M ETH) 也可以接受。随着 stake 数量的增长,长期高经济安全的前景逐渐开始减少。似乎完全有理由认为,如果奖励曲线使存款比率稳定在 d=0.25,那么 20 年后的 Ethereum 将比 d=0.75 时具有更高的经济安全性——只要 staking 集合的组成保持可行。当存款比率超过某些限制时,即使是短期安全性也开始降低,这与第 2.2 节中的推理一致。社交层可能会失去其中立性和可信度,而它本应是针对来自占主导地位的 SSP 的攻击的最终仲裁者。另一方面,确保存款规模不低于 14M ETH 也是合理的,这是 The Merge 时的主要规模(或者更准确地说,存款比率不低于 d\approx0.12)。至少这样的下限确保了 Ethereum 永远不会在 stake 参与方面冒险进入未知领域(如前所述,无法确保 stake 的价值保持在相对于所保护价值的某个特定水平)。
对经济安全性的讨论强调了确定正确存款比率所涉及的复杂性。事实上,由于几个关键变量的不确定性,没有一个特定的比率始终能最大化整体效用。最合适的存款比率可能会随着供应曲线的形状和提供一定安全水平的成本而变化。如果与 staking 相关的隐含成本较高(如图 1 所示),那么拥有略低的存款比率似乎是合理的,而不是成本较低的情况。这是首先使用奖励曲线的原因之一——它允许 Ethereum 根据该安全性的价格调整安全级别。因此,Ethereum 应该以存款比率范围为目标,该范围可能相当广泛,允许供应曲线影响 stake 的均衡数量。所提出的奖励曲线——在作者看来,并在完全实施的情况下——平衡了 Ethereum 的许多需求,包括短期和可能长期的可行经济安全性(有关其他细微差别,请参见第 6.3 节)。
表 3 显示了协议将在先前讨论的存款规模下提供的收益率,前提是当前的 REV 水平。此外,还提供了 REV 完全消失后的结果。请注意,如果 Ethereum 采用 MEV 销毁并且有明确的需求,则相关的硬分叉可以应用专门的调整来重新校准发行量。另一方面,如果未来几年供应曲线下降并且社区内达成协议,则可以将引入 MEV 销毁视为调节 stake 数量的最后一步。
| A: y_i | y_i+y_v | B: y_i | y_i+y_v | C: y_i | y_i+y_v | |
|---|---|---|---|---|---|---|
| 14M | 3.14 % | 5.28 % | 2.83 % | 4.97 % | 2.22 % | 4.37 % |
| 24M | 1.98 % | 3.23 % | 1.88 % | 3.13 % | 1.70 % | 2.95 % |
| 30M | 1.60 % | 2.60 % | 1.58 % | 2.58 % | 1.52 % | 2.52 % |
表 3. 在完全减少发行量的情况下,各种相关存款规模的 staking 收益率。
第一列表明,即使没有 REV,在选项 A 下,stake 数量也将保持在健康水平。假设至少有 24M ETH 仍以 2 % 的收益率进行 staking 是合理的。当然,如果提供 3.1 % 的收益率,仍将有 14M ETH 被 staking。然而,如果出于某种原因对此感到担忧,那么可以选择稍微向后移动奖励曲线的峰值,同时提高 F。例如,分级方法可以具有介于 25M 到 2^{25} 之间的 k 值,以及在 20M 左右的完全减少;两者都具有大约 10^{2} 的基本奖励因子。可以注意到选项 C 下的较低收益率,这是从安全角度来看,对于此选项,低于 F=32 的基本奖励因子是不理想的原因之一。表 4 反而显示了分级方法下的结果。
| Ag: y_i | y_i+y_v | Bg: y_i | y_i+y_v | Cg: y_i | Cg: y_i+y_v | |
|---|---|---|---|---|---|---|
| 14M | 3.68 % | 5.82 % | 3.53 % | 5.67 % | 3.06 % | 5.20 % |
| 24M | 2.50 % | 3.75 % | 2.46 % | 3.70 % | 2.33 % | 3.58 % |
| 30M | 2.10 % | 3.10 % | 2.10 % | 3.10 % | 2.09 % | 3.09 % |
表 4. 在分级方法下,各种相关存款规模的 staking 收益率。
5.2 共识激励
减少发行量会改变分配给共识参与者的各种角色之间的平衡。特别是,提议者将获得更大比例的所有奖励,这可能会威胁共识的稳定性。如果为证明义务提供的收益率 y_a 变为 staking 收益率 y 的一小部分,y_a/y,那么可以预期 staker 在最大化利润时会从事不规则和不利的活动,并且共识过程可能会崩溃。例如,他们甚至可能完全停止证明以避免被 slashing 的风险。所提出的奖励曲线旨在在当前的 REV 水平下,使证明者获得至少一半的奖励,如图 15 所示。如果 REV 大幅上升,则可以提高错过目标投票(并且可能错过来源投票)的惩罚,以便为正确执行证明者义务提供适当的激励。
图 15. 在 30 万 ETH REV/年的情况下,为所分析选项的证明提供的 staking 收益率比例 (y_a/y)(虚线为分级方法)。
5.3 劝退攻击
劝退攻击是一种针对区块链的诚实共识参与者的恶意行为,攻击者可能会为此付出代价,以从剩余奖励的竞争减少中获利。Buterin 概述的传统场景涉及多数攻击,但目前存在一些可能的少数劝退攻击针对 Ethereum。这些包括审查同步委员会证明、在非活动泄漏期间扣留证明,以及审查头部和可能的来源投票(在后续 slot 中拾取 stray 投票)。在非活动泄漏期间扣留证明是一种特殊情况,因为攻击可以直接获利。由于受害者损失的 ETH 是攻击者的七倍,并且还收到了与其损失大小相等的惩罚,因此审查同步委员会证明的 griefing 因子为 G=14。
“p-弹性”——捕捉奖励曲线上需求的负倒数点向收益弹性——是检查其对劝退攻击的敏感性的相关宏观措施。如果 p-弹性很高,那么攻击变得(更)有利可图。具体来说,对于小型 epsilon 攻击,盈利的条件是
a+Ga-1 > \frac{q}{p},
其中 G 是 griefing 因子,a 是攻击者持有的 stake 比例,q 是供应的点向逆收益弹性。这个简化的表达式没有说明利润的水平,利润可能非常小。这篇文章的篇幅太窄,无法对这个复杂的主题进行完整的阐述,有关内容即将发布。这种简化的目的是概括地说,随着 p 的上升,所需的 griefing 因子或攻击者持有的 stake 比例会下降。仅通过发行收益计算的 p_i-弹性可以通过将存款规模的百分比变化 \Delta D/D 与需求曲线上发行收益的百分比变化 \Delta y_i/y_i 联系起来确定
p_i = -\frac{\Delta y_i/y_i}{\Delta D/D}.
p_i-弹性可以用作评估奖励曲线的参考点,因为如果它适中,那么无论 REV 的大小如何,p-弹性都将是适中的。图 16 绘制了跨存款规模的 p_i-弹性。对于选项 A,p_i-弹性平稳上升,在 staking 120M ETH 时达到略低于 1.3 的最大值。从劝退攻击和卡特尔攻击(在第 5.4 节中描述)的角度来看,越低越好,但略高于 1 应该是完全可以接受的)。由于发行量从未下降,选项 B 的 p_i<1,而选项 C 与当前跨存款规模的奖励曲线相同。请注意,对于收益变为负值的奖励曲线,p_i-弹性(并最终如果收益继续下降,则 p-弹性)变为无穷大(请参阅先前文章中的图 40,显示了依赖于经济上限的方法的 p_i-弹性)。然而,均衡 p-弹性以及劝退攻击的盈利能力也将始终取决于供应曲线。
图 16. 本文中检查的三个奖励曲线的点向负倒数收益需求弹性(p_i-弹性)(越低越好)。
对抗少数劝退攻击的最佳防御措施是拥有一个平衡良好的共识机制。因此,Ethereum 未来应该修复当前的激励机制,该机制允许在非活动泄漏期间获得无限的利润率,以及允许 G=14 的攻击。第二个最佳防御措施,特别适用于较大的攻击者(包括多数),是某种形式的社会干预,如第 5.1 节所述。社会干预的前景可以使劝退攻击的风险回报率相当不利。直接收益相当低(事实上在大多数情况下为负),并且利润随着 stake 或 unstake 决策中的摩擦而变化。最后,请注意,能够首先依赖社会干预的前景也可能取决于 stake 数量,如第 2.2 节所述,从而使问题具有多维性。为了平衡本小节中讨论的各个方面,需要一个奖励曲线,该曲线为足够的 stake 数量提供适当的保证,而不会提供过度的发行量,然后通过逐渐衰减发行量来减少在广泛范围内 stake 的激励。这是拟议奖励曲线(选项 A)的设计原理之一。
5.4 卡特尔攻击
卡特尔攻击是与劝退攻击相关且重叠的假设结构,它们在合理化和执行方面可能有所不同。这里将简要介绍它们。卡特尔攻击包括 SSP 共同努力,试图减少它们自己和其他人之间的 stake 数量。当发行量随着 stake 数量的减少而增加 (p_i>1) 时,所有 staker 都可以尝试同意减少他们的 stake,并且每个人都会变得更好。这种框架可以为说服社会层在 staking 卡特尔试图抑制 Ethereum 的 permissionlessness 时不要干预提供合适的背景。理想情况下,对于卡特尔来说,它将能够依赖于共识机制之外的某种 permissioned 收入,多数人可以提取这些收入来激励最初的参与。然而,如果不足(特别是一旦收益上升),卡特尔可能会在共识机制内采取更险恶的行动。这些行动不需要完全破坏共识的形成才能有效。对“破坏者罢工”进行适度的劝退攻击,以确保此类实体“停止减少每个人的奖励”可能就足够了。
如果奖励曲线过于刻意地针对某些特定的 stake 数量,但仍然在较低数量时提供较高的发行量,那么 staker 可能会面临一种情况,即卡特尔化和 stake 数量的减少可能导致每个人的奖励高出数倍。提议的奖励曲线(选项 A)纳入了足够小的发行量减少,因为 D 增加,因此执行卡特尔攻击的理由是最小的/不存在的。
6.结论与讨论
6.1 影响奖励曲线最佳形状的因素
Ethereum 在决定奖励曲线时必须权衡许多因素。较低的发行水平:
- 通过不强迫用户承担不必要的成本来提高总体效用。这至关重要,并且这是每个 ETH 持有者都可以从降低的发行水平中受益的原因。
- 使 stake 数量保持适中。这减少了:
- 受损的社会层带来的风险,
- 巩固占主导地位的 SSP 的网络外部性,
- 占主导地位的 SSP 的规模经济。
然而,如果收益率降低到在合理高效的设置下 stake 变得无利可图的程度,那么过低的发行水平可能会使 solo(家庭)staker 在未来被淘汰。保留可行比例的 solo staker 将取决于所有 staker 之间的保留收益率分布,考虑到 solo staking 的初始外生激励(例如,空投)已经耗尽并且初始硬件投资已达到其折旧期限的情形。
从安全的角度来看,在较低的 stake 数量下保持较高的收益率是有益的,以确保有足够的 stake 数量和经济安全性。但是为了防止劝退攻击和卡特尔攻击,如果发行量在任何时候都不会急剧下降,也是有益的,即最好是 p_i-弹性保持相当适中。因此,这也成为一种平衡行为,最好是在任何存款规模下发行量都不会太高也不会太低。
区块提议者捕获的 MEV 带来了额外的复杂性:
- 它提高了预期收益率,因此需要较低的发行量来强制执行相同的 stake 数量。
- 但是,如果不损害当前规范下的共识激励,就不能过度减少发行量。诸如 staking 费用之类的解决方案可能会进一步削弱 solo staking 相对于委托 staking 的地位。
- 它提高了宏观层面预期均衡收益率的可变性,从而使实现任何特定的所需均衡变得复杂。
- 它提高了单个 solo staker 的预期收益率的可变性,如果发行量设置得太低,则会导致一些效用降低。
6.2 最佳奖励曲线
6.2.1 选项 A – Ethereum 的最佳替代方案
候选奖励曲线选项 A 旨在有效地调节发行量,同时允许 Ethereum 保留适当的共识激励,并使 solo staking 可变性保持在可接受的范围内。第 2.1 节强调了最低可行发行量的不可否认的好处——降低了 Ethereum 用户的隐含成本以及相关的总效用增益,这很可能使均衡状态下的每个人都变得更好。第 2.2 节通过讨论中立的社会层面的明显好处来进一步加强了这种情况,它可以确保 Ethereum 在预期的共识过程下运行。选项 A 将最好地获得这些好处,并且由于它对各种相关权衡采取了平衡的方法,因此在先前的研究中,甚至选择了比更严格的发行政策更好的该选项。目前尚不清楚哪种发行水平将最大化 solo staker 的比例(并且结果可能随所考虑的时间尺度而变化),第 4.2 节中回顾了两个方向的论点。重要的是,并没有严格强制执行少量的 stake,从而可以确保运行 staking 节点的成本相对于收益率而言不会过高。最终,这使得 staker 之间的偏好和情况的多样性在塑造 staking 集合的组成方面发挥了更核心的作用。提议的奖励曲线还确保了短期和长期的经济安全性,同时通过逐渐衰减发行量和适度的 p_i-弹性,对劝退攻击和卡特尔攻击具有足够的抵御能力,从而保留了完整的社会层。
选项 A 的另一个好处是其易于解释:单个可调变量定义了峰值发行点以及发行量相对于当前奖励曲线减半的点。正如第 2.3 节中指出的那样,损害经济主体的预测能力会损害福利。在考虑到潜在的未来 MEV 销毁实施的情况下,还需要根据不确定的未来 stake 增长和 solo staking 保留情况进行重新评估。因此,在可能的情况下,最好逐步减少发行量,从而允许逐步适应。
总而言之,作者认为,整体发行政策使选项 A(候选奖励曲线)成为 Ethereum 最合适的奖励曲线:
y_i=\frac{cF}{\sqrt{D}(1+D/k)}.
完全设想的减少构成 k=2^{25}。作者认为,最好采用 k=2^{26} 的分级方法。这仍然是一个足够实质性的改进,可以保证与改变发行政策相关的多方面治理过程,并且可以使 Ethereum 在未来发展中处于更有利的位置。从安全的角度来看,这种改变不会带来风险,因此 Ethereum 可以在治理过程结束后随时进行。确切的设置应在该治理过程中确定,并将基于在该过程中可能演变的情况。目前尚不能明确排除诸如将 k 设置为 2^{25}, 2^{27} 或 10^{8} 之类的替代方案。
6.2.2 选项 C – 备选方案
第二好的选择是降低基本奖励因子,即选项 C。可以注意到两件事:(1)共识规范更改更加最小,(2)(solo)staker 的保证收益更高。当然,对许多人来说,(2)反而会被认为是缺点,因为它会导致更高的均衡 stake 数量,从而使这方面的问题结果与选项 A 相比更有可能发生。即使最终目标是选项 A,仍然可以使用选项 C 采取第一步。但是,作者认为最好继续使用选项 A,给社区一个清晰的路径和路线图。选项 B,也许 F=64,是 A 和 C 之间的折衷方案,如果它们之间无法达成协议,则可以调用它。
6.3 未知的结局
Ethereum staking 经济学的最佳“结局”目前尚不清楚,并且可能会持续至少十年。这取决于许多目前尚未解决的方面,其中之一是结局共识机制本身的规范。
但是,有理由相信所提出的奖励曲线可以在很长一段时间内保持可行,也许永远。例如,考虑这样一种情况,即社区认为控制 stake 数量很重要。然后,可以在不远的将来以 k=2^{25} 实现完全减少,并在启动 MEV 销毁时保持不变。另外两种选择是,一旦可以实施 MEV 销毁,就返回到 k=2^{26},或者在 k=2^{26} 处停止:如果 MEV 销毁被证明是可行的,并且社区对此感到满意,则将其作为第二步。在 k=2^{25} 和 MEV 销毁的情况下,staking 收益率确实会变得相当低(请参阅这篇文章的图 33 中的石灰颜色曲线)。例如,在 stake 60M ETH 的情况下,发行收益率为 0.77 %。在考虑到风险(slashing、智能合约、治理等)以及其他 staking 成本的情况下,似乎不太可能以如此低的收益率将 stake 数量推高到 60M ETH 以上。然而,即使事实证明确实如此,也不应将其解释为认为提议的奖励曲线必须无限期地保持不变——只是它似乎非常适合作为结局,并且与当前的奖励曲线相比,提供了明显的改进。最佳 stake 数量最终取决于供应曲线的形状(表示可能的可以实现的收益率 - 数量组合),以及 Ethereum 平衡的各种权衡的相对重要性将如何在未来演变。
即使在采用提议的奖励曲线之后,对于结局,仍然有一件事可以肯定。在奖励曲线适应 D 而不是 d 的情况下,长期 staking 均衡最终也受到流通供应均衡的影响,因为流通供应将漂移到平衡供应、需求和协议收入。因此,一旦开始被跟踪,Ethereum 应该过渡到在奖励曲线公式中使用 d,这可以通过交换流通供应来简单地完成。
不发行超过严格安全所需的Token的好处确实是显而易见且巨大的。Schwarz-Shilling 和 Dietrich 提出了好处并论证了以低 stake 数量为目标的结局,可能通过经济上限(当 stake 过多的 ETH 时,收益会变为负无穷大)。当涉及到 solo staking 时,该分析着眼于一个假设的情景,其中在 stake 30M ETH 时的保留收益为 1.5 %,在 stake 120M ETH 时的保留收益为 2 %。在具有高保留收益率的平坦供应曲线下,在低 stake 数量下进行更严格的定位(收益率下降得更快的奖励曲线)实际上似乎相当简单。在这种供应曲线下,无论奖励曲线的形状如何,solo staking 始终是可行的。在图 12 的供应曲线下,严格的定位方法可能会迫使产生不利于 stake 集合组成的结果。关于供应曲线可能形状的先验知识在此很重要。随着 p-弹性被推得太高,劝退袭击和卡特尔袭击变得更容易可行。对于 solo staker 而言,关于收益是否会变为负数的 uncertainty 本身可能会使他们停止对硬件的投资。实际上,收益率或 stake 数量方面的确定性始终通过奖励曲线的形状来替代。更平坦的需求曲线将平滑收益率的波动,因此可以降低均衡收益率,ceteris paribus(在相同的 stake 数量下),这是因为经济主体可能愿意用较低的可变性来替代较低的回报。但是,更陡峭的需求曲线反而会减少 stake 数量的波动,并更好地保证其最大水平。作者逐渐改变了立场,从2021 年赞成严格的存款比率定位,到逐渐专注于定位理想的存款比率范围(为了平衡存在的权衡,合理的均衡范围可能会相当广泛),最终确定提议的奖励曲线是平衡与 MEV 相关的当前情况的正确机制,MEV 销毁的实施允许相同的奖励曲线可能过渡到可行的结局策略。然而,重要的是在接下来的十年中对新出现的信息保持开放态度,更新先验知识,并反思不断变化的权衡。
最后请注意,当内生收益为 0 或负数时,staking 没有直接的货币目的。因此,只有当 MEV 或例如 preconfirmation 的奖励落在提议者身上时,才需要负的发行收益率。因此,在所有当前具有负发行收益率的情况下,未汇集的 solo staker 将被迫接受每个 epoch 的负支出,同时等待提议者分配,而委托 staker 可能会定期获得小的正回报。在涉及到负发行收益率时,最有趣的选择是在特别不希望有的 stake 水平上进行非常逐渐的过渡,例如,从当前 y_i 的结构中减去 (D/k)^p,其中 p 设置为 0.5、1 或 2。在这种情况下,渐近接近 0 的奖励曲线可能更可行。最佳形状最终将取决于共识机制本身的发展方式(例如,solo staker 的角色)。然而,具有无限负发行收益率(由于流失限制,技术上可能无法达到)的构造将给 staker 带来更多 uncertainty,并且可能会给协议设计空间带来不必要的复杂性。
在 数量 维度上增加 时间 维度也值得考虑。在时间 - 数量策略下,奖励曲线在弹性方面保持适中,但允许整个曲线逐渐适应由均衡隐含的供应曲线的变化。因此,在提议的奖励曲线下,当 d 偏离理想水平时,k 会漂移,效果发生在数十年时间尺度上。这将允许 Ethereum 在设置奖励曲线时考虑供应曲线。该机制将平滑收益率的波动,并且延迟调整可能会使一些劝退袭击和卡特尔袭击变得不那么有吸引力。对于使用该策略 k 可能变得多小的程度,可以设置某些限制,以避免特殊的意外结果。此处还在自动增加收益率(为劝退袭击敞开大门)和降低收益率(为与低收益率相关的熟悉问题敞开大门)之间存在区别。有趣的是,尽管该协议可能无法确定谁是劝退式攻击的责任方,但它仍然能够确定它实际上正在受到攻击,从而为通过条件逻辑进行保护提供了途径。
6.4 对 ETH 持有者重要的比例
第 2.1 节、第 2.2 节和第 4 节中提出的见解对 Ethereum 的用户具有影响,无论他们是否持有大量的 ETH。拥有一个可行的社会层 —— 没有被任何 SSP 破坏 —— 最终关系到可信的中立性。拥有 solo staker 很重要,为委托 staking 拥有许多可行的选择也很重要。这些事情也特别与 ETH Token持有者有关。最终影响 ETH Token持有者最多的不是“按比例的收益”,而是由 Ethereum 驱动的世界经济的比例,包括 staker。如果发行政策降低了 Ethereum 的价值,那么最大化 y_p 毫无意义,当然对于不持有 ETH 的用户来说毫无意义,甚至对于 ETH Token持有者来说也没有意义,因为已降低价值的区块链的原生Token并不那么有价值。实际的“实际收益”包括相对于相关消费者价格指数,底层 ETH 的价值变化 —— 包括任何 staking 收益。然而,在一个经济系统中拥有健全的原生货币确实非常有用。并且,最好的健全货币不会让用户负担研究各种 SSP 可靠性、跟踪 staking 收入并看到其被征税的负担,或冒着在一次 slashing 事件或其他失败中被消灭的风险。
6.5 关于有限理性和收益的说明
有限理性的概念有助于解释为什么某些用户可能更喜欢 y_p 较低的情形,其中收益率提高,但供应通货膨胀率(用户很难跟踪)甚至更高。行为经济学在这方面可以帮助解释为什么一些经济主体可能会非理性地行为,可能是因为缺乏教育或没有时间来权衡某个主题。最近,一种依靠有限理性的扭曲论点已经出现在 SSP 或其投资者的几位代表的著作中。从本质上讲,支持者们认为,Ethereum 应该利用人们对收益的有限理解,并保持高收益来欺骗用户,让他们认为自己获得了收益,而实际上并没有。而不是教育人们这些事情,应该为了获得一些短期收益而降低用户效用,而这种短期收益不太可能实现。必须避免此类策略。
6.6 下一步
作者希望这篇文章已经使社区相信了调整发行政策的好处,并且可以回答你可能有的任何问题。这篇文章将作为提议的奖励曲线 —— 选项 A 的 EIP 的长篇参考。在单次硬分叉中进行完全减少似乎不明智,并且概述的逐步方法是有利的。那一步基本上没有缺点,将大大改善 Ethereum,而且如果不是最后一步,它仍然是朝着正确方向迈出的一步。
- 蓝壳策略 - 劝退最集中的参与者作为最佳路径
- 关于发行政策的实用结局
- 最大可行安全性:Ethereum 发行的新框架
- Orbit SSF:SSF 的 solo-staking-friendly 验证器集管理
- 以太坊 staking 市场正式框架的主要见解
- 更多 4 个
- 原文链接: ethresear.ch/t/reward-cu...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- GAS2ETH 簡介 769 浏览
- 21. 节点 & 验证者:因为显然更多计算机等于更好的真理 1832 浏览
- 104:ERC20:ETH资产世界的第一个“秩序” 717 浏览
- 如何质押Monad (MON) 464 浏览
- 理解 Solana 提案:SIMD-0411 792 浏览
- 在保加利亚推出首个 Solana 验证器 1412 浏览
- Bitwise选择Helius作为独家SOL质押提供商 626 浏览
- Solana公司选择Helius作为SOL质押提供商 668 浏览
- 037:Restaking & EigenLayer:二次质押是什么? 1213 浏览
- 加密货币市场本周回顾 (09/29/25) 1005 浏览
- 深入探索以太坊共识层:存款与提款 922 浏览
- 为什么重新分配代币比销毁代币更好 863 浏览
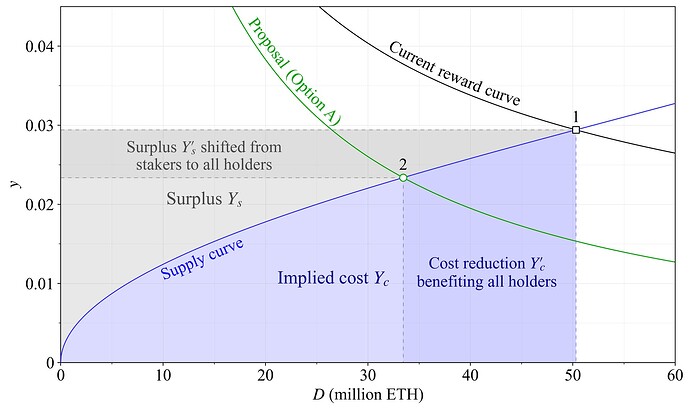 \
Figure 11920×1141 93.9 KB
\
Figure 11920×1141 93.9 KB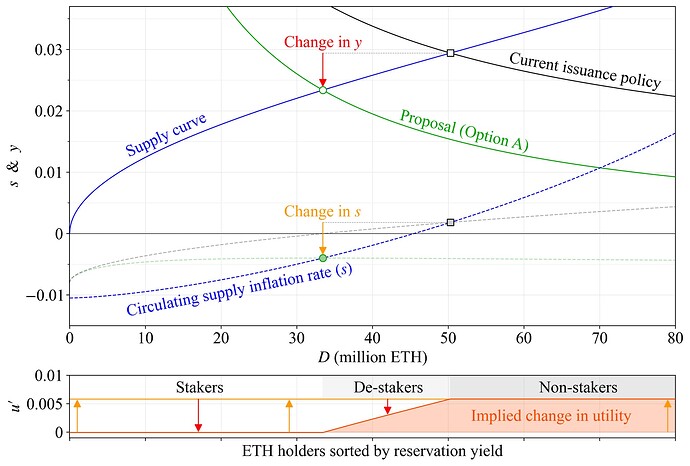 \
Figure 21920×1297 138 KB
\
Figure 21920×1297 138 KB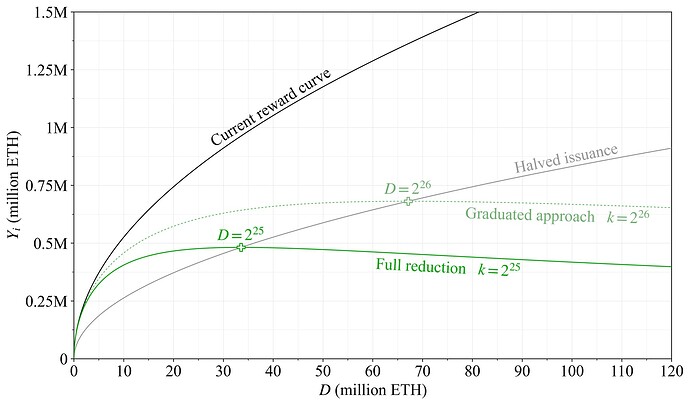 \
Figure 31920×1126 94.2 KB
\
Figure 31920×1126 94.2 KB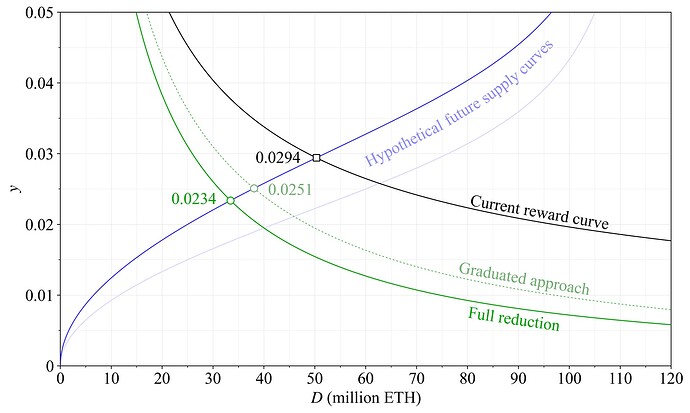 \
Figure 41920×1150 102 KB
\
Figure 41920×1150 102 KB \
Figure 51920×1056 124 KB
\
Figure 51920×1056 124 KB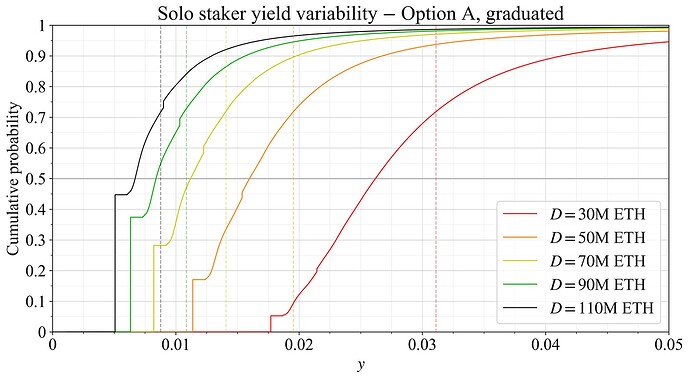 \
Figure 61920×1056 127 KB
\
Figure 61920×1056 127 KB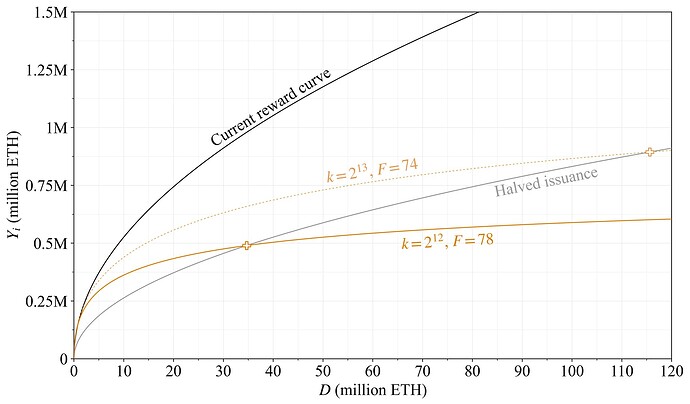 \
Figure 71920×1126 87.5 KB
\
Figure 71920×1126 87.5 KB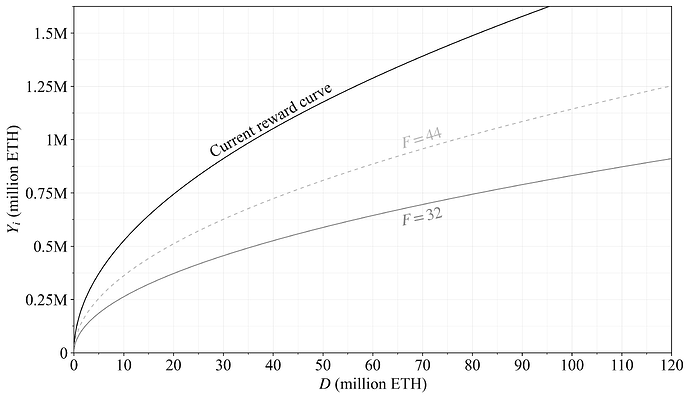 \
图 85368×3104 497 KB
\
图 85368×3104 497 KB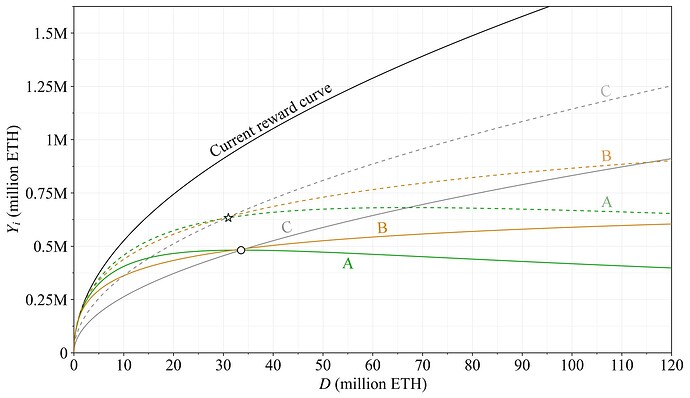 \
图 91920×1110 96.9 KB
\
图 91920×1110 96.9 KB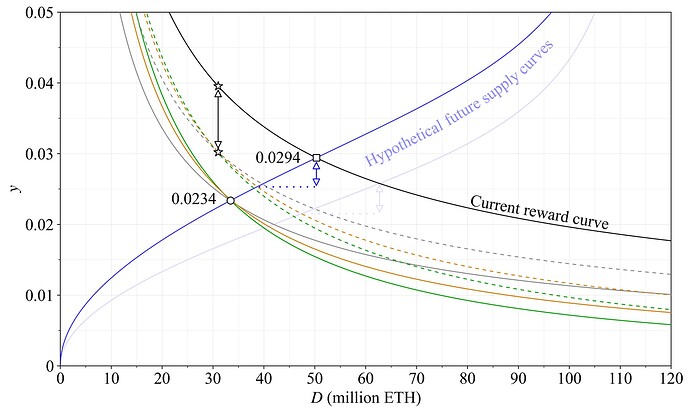 \
图 101920×1150 115 KB
\
图 101920×1150 115 KB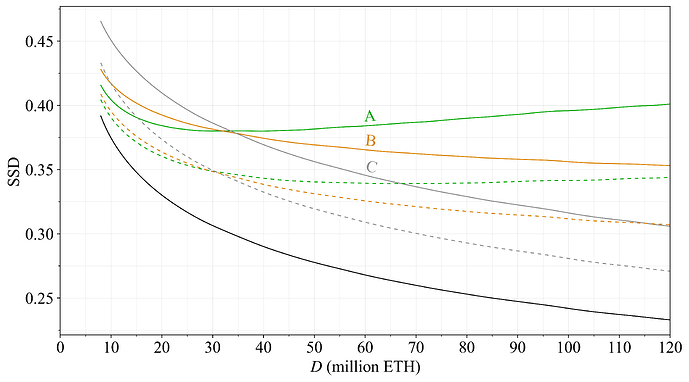 \
图 115253×2911 511 KB
\
图 115253×2911 511 KB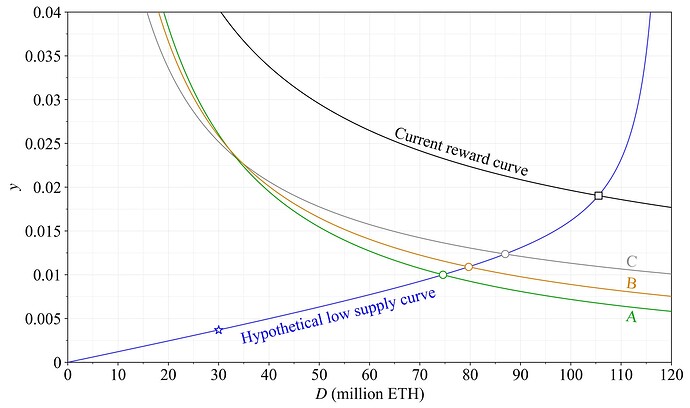 \
图 121920×1137 103 KB
\
图 121920×1137 103 KB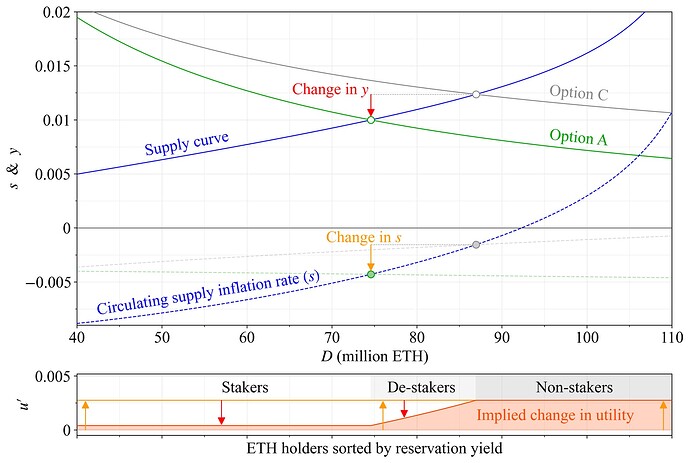 \
图 131920×1289 133 KB
\
图 131920×1289 133 KB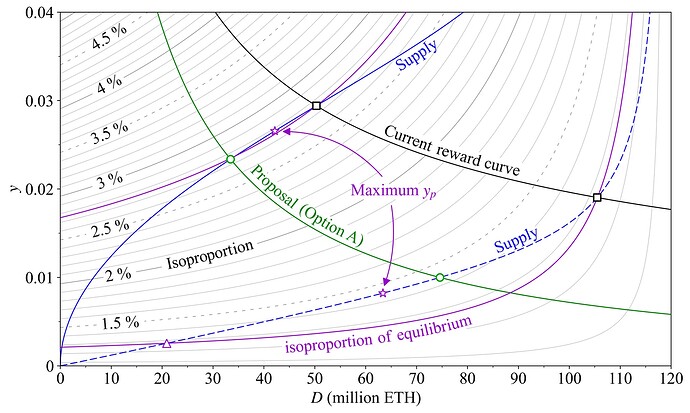 \
图 141920×1150 174 KB
\
图 141920×1150 174 KB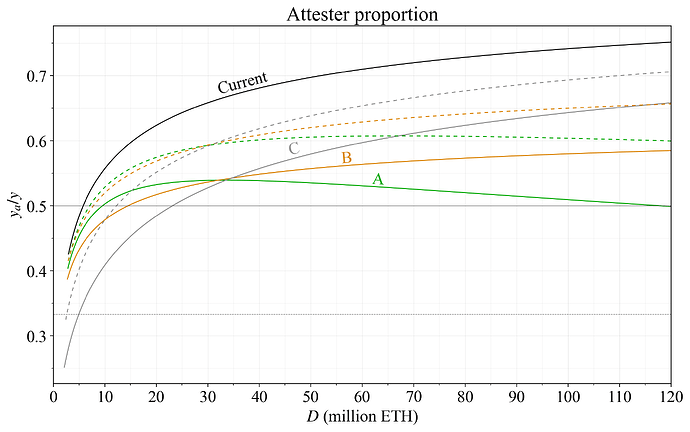 \
图 152078×1302 176 KB
\
图 152078×1302 176 KB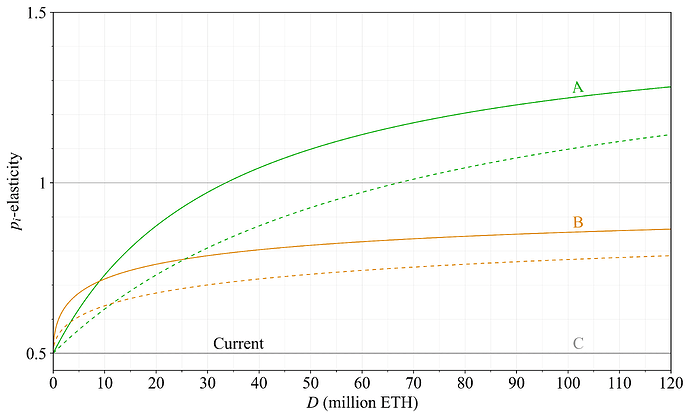 \
图 165194×3147 416 KB
\
图 165194×3147 416 KB
