Jolt技术详解：RISC-V零知识虚拟机 - ZKSECURITY

在我们的前一篇文章中，我们深入研究了 Jolt zkVM，并发现了代码中几个重要的错误。在这篇文章中，我们将详细介绍 Jolt 实际是如何工作的。

Jolt 是一个零知识虚拟机 (zkVM)，专为 RISC-V 架构设计，由 a16z 开发。它采用 Lasso 查找参数来证明 VM 执行的正确性。虽然 Jolt 经常被誉为最简单的 zkVM，但它是一个相对较新的协议，对其功能的解释资源有限。

这篇文章主要来源于 Jolt 源代码、Jolt 书籍 以及关于 Lasso 和 Jolt 的原始论文。

概述

在 Jolt 中，程序首先会被编译成 RISC-V 二进制文件。然后，Jolt RISC-V 模拟器将运行并执行该二进制文件，以生成执行跟踪。从这些执行跟踪中，证明者可以生成一个证明，该证明稍后可以由验证者进行验证。

下图来自 Jolt 论文，展示了如何证明执行跟踪的概述。

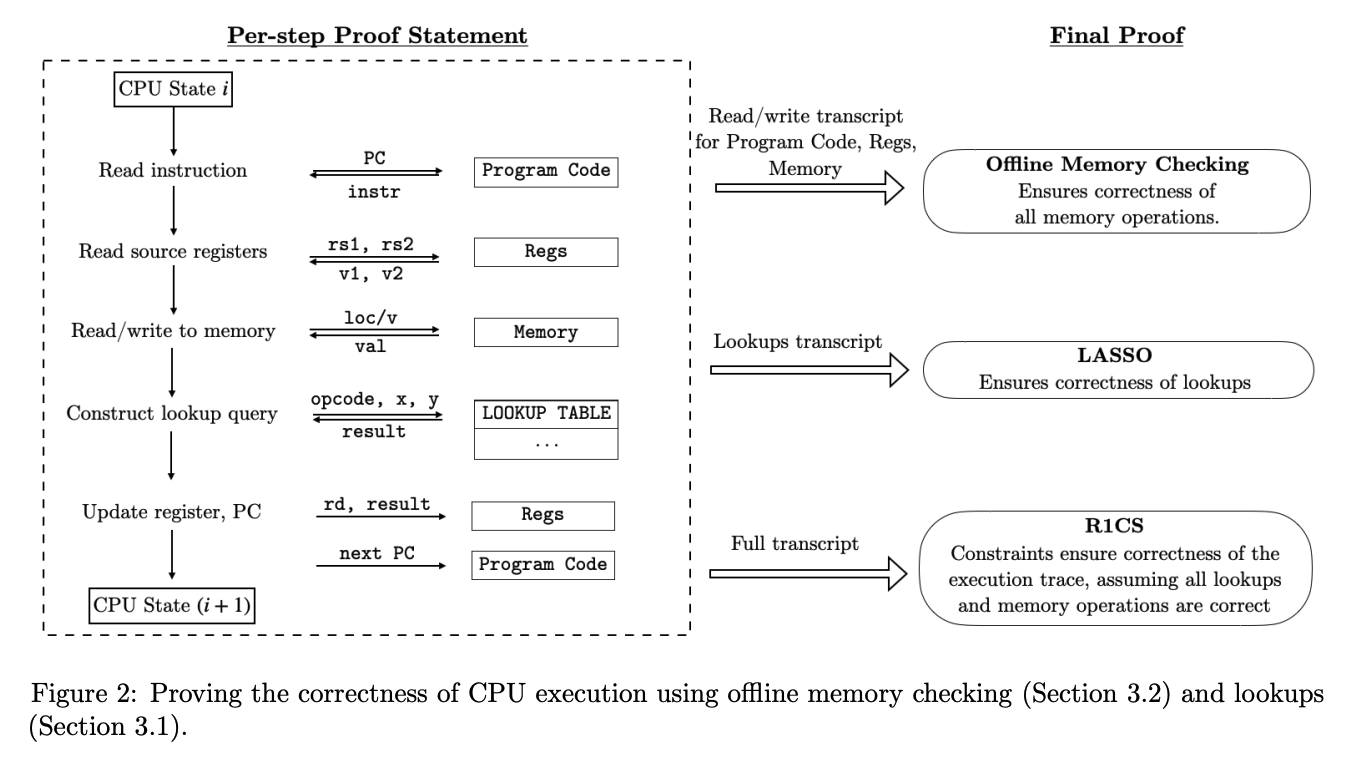
因此，根据上图，证明执行跟踪的正确性主要有三个组成部分：

1. 指令查找
2. 离线内存检查
3. Rank-1 Constraint System (R1CS)

在下一节中，我们将详细探讨每个部分。

指令查找

在 Jolt 中，VM 指令评估的正确性主要通过查找表来证明，这些查找表通过查找参数链接到证明系统。

本质上，查找参数是一种加密协议，允许证明者证明一组值存在于预定义的表中，而不会泄露关于计算的额外信息。例如，为了证明 1+2=3，我们可以简单地使用 1 和 2 作为索引在表 T 中进行查找，以获得结果 3。这可以使用一个名为 Lasso 的查找参数有效地完成。

考虑一个向量 T∈Fn 作为查找表，以及一个二元矩阵 a∈Fs×n 作为相应的查找索引，其中每行只有一个 1，表示表 T 的索引，n 和 s 分别是 T 的大小和查找的数量。

然后，查找参数使证明者能够说服验证者，值向量 v 包含在表 T 的索引 ai 中，即对于所有 i，T[ai]=vi。

朴素地，为了检查 T[ai]=vi，验证者可以简单地检查以下等式：

a⋅T=v

然而，这个简单的点积在实践中非常不切实际，因为这些值的大小非常大。因此，我们可以将上述等式检查转换为以下针对随机 r 的 sumcheck 协议实例

∑y∈0,1log⁡na~(r,y)⋅T~(y)=v~(r)

其中 T~, a~, 和 v~ 代表各自值的 multilinear extension (MLE)。

sumcheck 协议本身是一种交互式证明，它通过递归地将问题简化为单变量多项式来验证布尔超立方体上的多元多项式之和。sumcheck 协议和 MLE 的细节不在本文的讨论范围内。我们建议查看以下资源 here 以了解其工作原理。

继续我们之前的表达式，我们仍然可以进一步优化它。请记住，a 是稀疏的，其中每行仅包含一个 1，其他条目中为 0，因此我们可以重新表述左侧，使其仅对查找求和，而不是对表条目求和：

∑j∈0,1log⁡seq~(j,r)⋅T[dim(j)]=v~(r)

其中 dim(j) 是行 j 的查找索引，eq~(j,r) 是函数的 MLE：

eq(j,r)={1ifr=j0otherwise

但是，由于 T 非常大（对于 32 位，有 264 行），因此实现起来并不实际。我们可以将 T 分解为更小的块（例如，对于 32 位，每个块 4 位，即 c=16）。

∑j∈0,1log⁡seq~(j,r)⋅g(T1[dim1(j)],…,Tc[dimc(j)])=v~(r)

其中 g(x1,…,xc) 是一个 c 变量多项式，它是 f(x1,…,xc) 的 multilinear extension，充当将块“连接”在一起的整理函数。这些块在 Jolt 中称为“子表”。

由于 Ti[dimi(j)] 必须是多项式形式，我们可以将它们重新表述如下

∑j∈0,1log⁡seq~(j,r)⋅g(E1(j),…,Ec(j))=v~(r)

其中 Ei(j) 是表示证明者承诺的 Ti[dimi(j)] 的多项式。

这就是需要通过来自验证者的随机点 r 处的 sumcheck 计算的最终表达式。这在 Jolt 中称为“primary sumcheck”。

在 Lasso 协议中，证明者向验证者提供承诺 Ei。但是，到目前为止，验证者无法保证 Ei 实际上是来自 Ti 的值，以至于 Ei(j)=Ti[dimi(j)]。这就是为什么我们需要 Jolt 的第二个组成部分，称为离线内存检查。

离线内存检查

离线内存检查是 Jolt 的第二个组成部分。它允许证明者说服验证者正确执行了读取/写入操作。

在 Jolt 中，内存检查用于三个不同的位置：

1. 指令查找： 确保指令查找操作中的 Ei 是正确的
2. 字节码： 确保执行跟踪是实际程序字节码的一部分
3. 内存读/写： 确保读/写内存（寄存器、RAM 和程序 I/O）是正确的

本质上，离线内存检查允许验证者确保对特定内存地址的读取操作返回该地址最近写入的值。

首先，让我们定义四个集合 init、final、read 和 write，它们分别表示初始、最终、读取和写入的内存集合：

init,final⊆(ai,vi,ti)|i∈[0,M]

read,write⊆(ai,vi,ti)|i∈[0,m]

这里，a,v,t 分别表示地址、值和时间戳（内存访问计数器），其中 M 是内存大小，m 是内存操作的总数。

基本上，验证者可以使用以下等式检查内存操作的正确性，而与元素的顺序无关：

read∪final=write∪init

我们可以有效地对每个集合应用多重集哈希来执行相等性检查，而不是单独检查元素。

因此，检查变为

Hγ,τ(read)⋅Hγ,τ(final)=Hγ,τ(write)⋅Hγ,τ(init)

使用以下同态哈希函数 H

Hγ,τ(S)=∏(ai,vi,ti)∈Shγ,τ(ai,vi,ti)

其中 h 是来自验证者的随机 γ 和 τ 的 Reed-Solomon 指纹：

hγ,τ(a,v,t)=a⋅γ2+v⋅γ+t−τ

在 Jolt 实现中，此多重集哈希 H 由乘法门的二叉树电路表示，并使用优化的 GKR 协议计算。因此，每个叶子是每个集合元素的 h 的计算结果。

考虑来自 Jolt 存储库 的下图，以更清楚地了解哈希的表示方式：

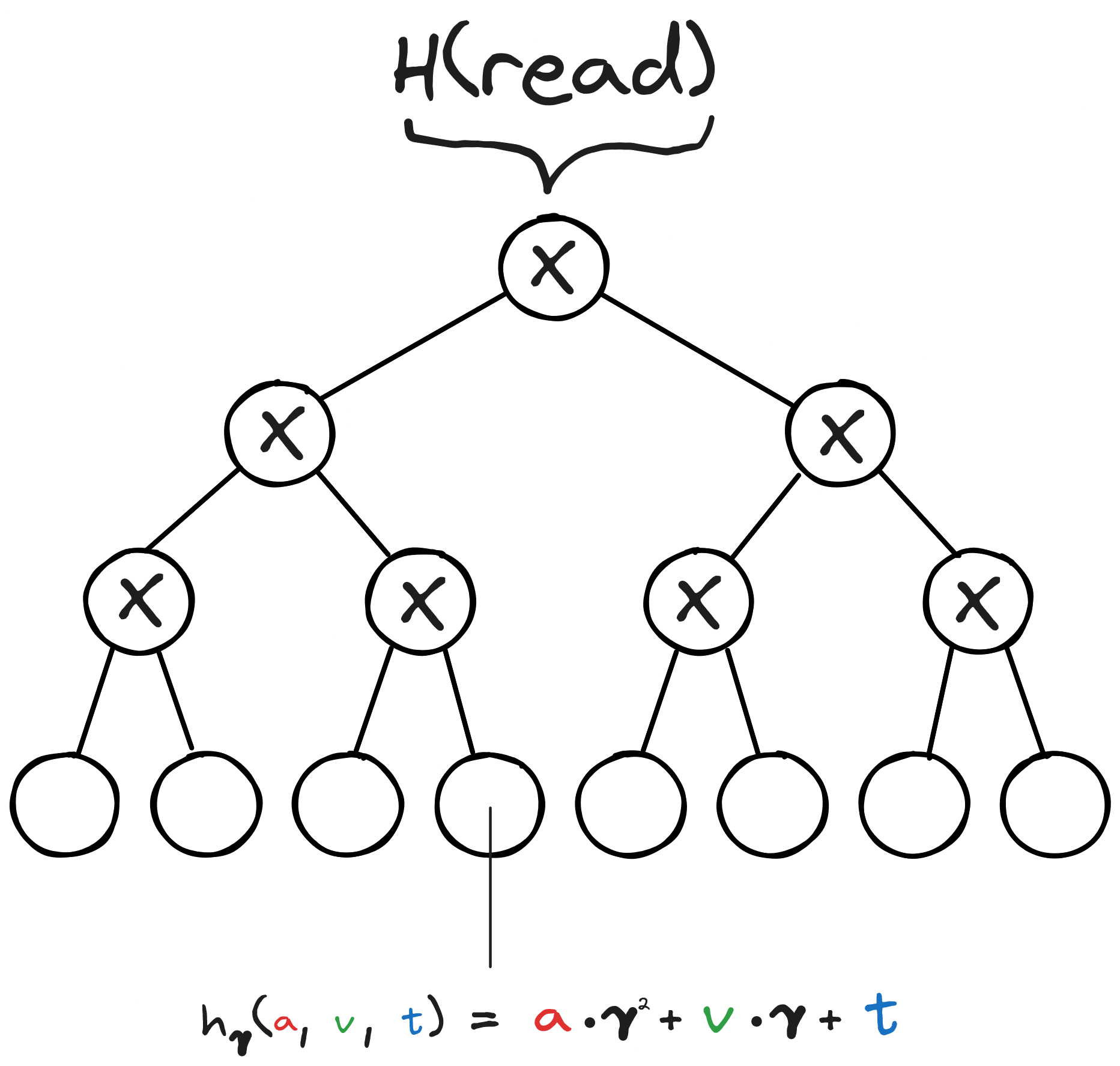
指令查找中的内存检查

继续我们之前的指令查找解释，为了确保 Ei(j)=Ti[dimi(j)]，我们可以将此问题转换为 T 被读取 log⁡s 次的内存检查。换句话说，Ei(j) 和 dimi(j) 分别等效于 vi 和 ai。内存检查将确保存储器地址 ai 的读取操作确实是值 vi。

首先，验证者可以轻松构建 init 内存集，其中对于所有 i，ti 均为零，并使用以下公式计算每个叶子的 MLE：

hγ,τ(initi)=(∑i=1log⁡M2i−1⋅ki)⋅γ2+Ti~(k)⋅γ+0−τ

对于读取和写入内存集，验证者需要读取内存地址的列表，该列表在证明者承诺中用 dimi 表示，以及来自 Ei 的值和来自 read-ctsi 和 read-ctsi+1 的时间戳分别用于读取和写入。

hγ,τ(readi)=dimi(k)⋅γ2+Ei(k)⋅γ+read-ctsi(k)−τ

hγ,τ(writei)=dimi(k)⋅γ2+Ei(k)⋅γ+read-ctsi(k)+1−τ

final 内存集的程序类似于 init 内存集的程序。主要区别在于时间戳是从 final-ctsi 计算得出的，final-ctsi 表示查找总数，查找总数也由证明者承诺。

hγ,τ(finali)=(∑i=1log⁡M2i−1⋅ki)⋅γ2+Ti~(k)⋅γ+final-ctsi(k)−τ

字节码中的内存检查

在 Jolt 中，单个 CPU 步骤（例如 add x0, x0, x0）由所谓的字节码表示。每个字节码元素包含以下值：

• address：二进制文件中指令的内存地址
• bitflags：打包的二进制标志，用于确定指令的类型和属性，并在以后在 R1CS 中使用
• rd：指令目标寄存器的索引
• rs1：指令第一个源寄存器的索引
• rs2：指令第二个源寄存器的索引
• imm：指令的立即数值

为了检查正在证明的执行跟踪是否是程序实际字节码的子集元素，我们可以简单地使用内存检查来证明表 T 的读取操作，表 T 是程序字节码。

但是，此过程中使用的集合元素略有不同。每个集合元素不是 (a,v,t)，而是 (a,vbitflags,vrd,vrs1,vrs2,vimm,t)。

因此，要计算 h，计算变为：

a⋅γ6+vbitflags⋅γ5+vrd⋅γ4+vrs1⋅γ3+vrs2⋅γ2+vimm⋅γ+t−τ

请注意，在此部分中，证明者不需要提供任何承诺，因为假定程序字节码足够短，并且验证者可以自行计算 MLE。

读/写内存中的内存检查

zkVM 程序需要处理并将程序输入和输出公开给验证者，以便可以检查它们是否与某些语句匹配。

但是，正如我们在离线内存检查中看到的那样，验证者实际上并不完全了解内存值。那么，Jolt 如何处理这个问题呢？

首先，让我们看看读写内存结构是如何在 Jolt 中映射的：

Jolt 中的读写内存被构造为一个统一的地址空间，该空间分为三个主要区域，分别是寄存器、程序 I/O 和 RAM。

寄存器是所有 VM 寄存器和虚拟寄存器所在的内存区域。对于 32 位架构，此区域的大小为 26（32 个 VM 寄存器和 32 个虚拟寄存器）。

程序 I/O 包含输入、输出、panic 位、终止位和零填充，直到此区域的大小是 2 的幂。此区域中的所有值都为验证者所知。

RAM 是堆栈和堆所在的内存区域。该区域也用零值填充，直到整个内存大小是 2 的幂（这是之前设置的最大内存大小）。

为了检查寄存器和 RAM 的正确性，我们可以像往常一样通过将寄存器和 RAM 组合为一个集合元素来执行离线内存检查。但是，对于程序 I/O，我们需要执行额外的检查。

请注意，由于输入为验证者所知，其余为零，因此验证者可以自行计算 init 的 MLE。但是，由于寄存器和 RAM 在 VM 执行过程中对验证者未知，因此他们无法计算 final 的 MLE。

验证者可以做的是计算程序 I/O（即 io）的 MLE 等于 final。可以通过 sumcheck 协议执行此等式检查，以强制对 io 和 final 的差进行“零检查”：

∑x∈0,1log⁡Meq~(r,x)⋅io-range~(x)⋅(final−io)=?0

其中 io-range~(x) 是函数的 MLE：

io-range(x)={1ifio-start≤x≤ram-offset0otherwise

io-start 和 ram-offset 分别表示程序 I/O 和 RAM 在内存中的偏移索引。

但是，我们仍然需要注意最后一件事。到目前为止，我们处理的是只读内存检查。但是这一次，为了确保寄存器和 RAM 的正确性，之前的多重集相等检查是不够的，因为寄存器和 RAM 是可写内存。

在读写上下文中，我们需要额外的检查来验证每个读取操作不得检索将来写入的值。

本质上，验证者需要确保存储器操作的时间戳（称为读取时间戳）小于或等于全局时间戳。此全局时间戳从 0 开始，每次递增 1。

此问题等效于检查读取时间戳和从全局时间戳中减去读取时间戳的值是否在范围 [0,m) 内，其中 m 是执行跟踪的长度。因此，这基本上是一个范围检查，可以通过 Lasso 将此问题视为查找表 [0,1,…,m−1] 来完成。

总而言之，为了检查读写内存操作的正确性，我们需要执行三件事：

1. 离线内存检查
2. 通过 sumcheck 处理程序 I/O
3. 通过 Lasso 进行时间戳范围检查

Rank-1 Constraint System (R1CS)

我们已经处理了指令被正确执行，并且所有内存操作都通过了前两个组件的正确性。

但是，我们尚未处理以下情况：

• 执行跟踪按照字节码地址和程序计数器 PC 以正确的顺序排列（包括跳转和分支）
• 指令查找使用来自实际操作数的正确的查找索引（无论是 rs1、rs2 和/或 imm）
• 指令查找输入和输出与从/向内存读取/写入的值一致

为了处理这些问题，Jolt 的最后一个组件确保整个 VM 过程（fetch-decode-execute）通过 R1CS 正确地粘合和约束所涉及的步骤。

Jolt 中的完整约束可以在 constraints.rs 中看到。

请注意，Jolt 中的大多数 R1CS 约束都是统一的，因此整个程序的约束矩阵与单个 VM 指令的约束的相同副本。唯一非均匀的约束是检查 PC 到下一步转换的约束。

R1CS 输入 & 位标志

给定矩阵 A,B,C∈Fm×m，当且仅当

(A⋅z)∘(B⋅z)−(C⋅z)=0

时，R1CS 的可满足性为真

其中 A、B、C 是约束，z 是 R1CS 的见证。这就是证明者需要证明他们知道这样的 z 的原因。因此，每个约束必须采用 a⋅b−c=0 的形式。

为了构造这些约束，Jolt 使用来自执行跟踪的输入，其中每个跟踪（单个 CPU 步骤）包含字节码元素、指令查找和读写内存操作。

Jolt 还使用来自字节码的位标志作为 R1CS 输入，以“切换”某些约束。例如，如果我们只想在标志为真时检查 x 和 y 的相等性，则 R1CS 约束如下：

flag⋅(x−y)=0

位标志是 64 位长度的二进制文件，其中包含两个单独的标志连接在一起，称为 电路标志 和 指令标志。

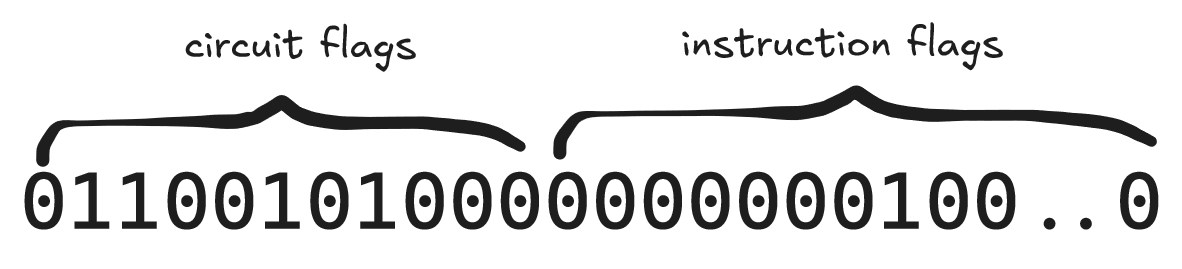
电路标志是可以设置的多个标志，以匹配指令的特定属性。以下是 Jolt 中实现的电路标志的完整列表：

1. 第一个查找操作数是 PC 吗？
2. 第二个查找操作数是 imm 吗？
3. 这是一个加载指令吗？ 04.这是一个存储指令吗？
4. 这是一个跳转指令吗？
5. 这是一个分支指令吗？
6. 此指令更新 rd 吗？
7. 此指令是否涉及查找的连接？
8. 这是一个虚拟指令吗？
9. 这是一个断言指令吗？
10. 此指令是否需要不更新程序计数器 PC？

请注意，以上列表取自 当前 Jolt 代码（在撰写本文时），该代码与 Jolt 论文的 附录 A.1 中描述的略有偏差。

同时，指令标志是单个标志（one-hot 向量），用于确定执行的指令类型（是加法、减法还是乘法？）。因此，例如，ADD 和 ADDI 指令将使用相同的指令标志。

例如，假设我们要构建一个约束，以确保写入 rd 的值等于指令查找输出。

让我们将 rd_bytecode 定义为程序字节码中 rd 的值，将 flag7 定义为第 7 个电路标志的值。首先，我们设置一个辅助变量 condition：

condition←rd_bytecode⋅flag7

如果 rd_bytecode 和 flag7 也都非零，则此变量应为非零。

请注意，我们需要添加约束，以使 condition 实际上等于 rd_bytecode⋅flag7。否则，这会成为约束不足的错误：

rd_bytecode⋅flag7−condition=0

然后，主要约束如下：

condition⋅(rd_write−lookup_output)=0

此处，rd_write 是从读写内存操作写入 rd 的值，lookup_output 是指令查找的结果。此约束确保 rd_write 必须等于 lookup_output。

R1CS 满足性

在构造 R1CS 约束和见证之后，Jolt 使用 Spartan 来证明给定见证的 R1CS 满足性。

Spartan 的工作原理的详细信息不在本文的讨论范围之内。简而言之，Spartan 本质上是将 R1CS 实例转换为 sumcheck 实例，可以通过使用两个 sumcheck 协议有效地证明这些实例。它还需要多线性多项式承诺方案（例如 Hyrax、HyperKZG 等）来承诺对给定见证的评估。

将它们放在一起

让我们组合所有 Jolt 组件，并总结一下完整协议是如何执行的。

请注意，在实践中，我们使用非交互式版本，其中所有验证者随机挑战都是从 Fiat-Shamir 启发式生成的。

设置

在设置阶段，证明者和验证者都同意以下内容：

1. 将在整个协议中使用的多项式承诺方案（包括结构化参考字符串 (SRS) 和用于相关 PCS 的曲线）
2. 可证明程序的字节码
3. 用于分解表查找的块大小
4. 最大内存大小

然后，证明者和验证者可以分别根据商定的块大小和最大内存大小构造查找子表和内存布局。

证明

证明者使用一些给定的输入运行可证明的程序，然后生成执行跟踪和程序 I/O。

从生成的执行跟踪和程序 I/O 中，证明者按顺序执行以下操作：

1. 填充执行跟踪，直到跟踪长度是 2 的幂，并用 NOP 指令填充。
2. 通过离线内存检查证明执行跟踪中的字节码是设置阶段中字节码的一部分。
3. 通过主 sumcheck 和离线内存检查证明执行跟踪中的所有指令查找都是正确的。
4. 通过离线内存检查证明执行跟踪中的所有读写内存操作都是正确的。
5. 通过 sumcheck 协议证明程序 I/O 有效。
6. 通过时间戳范围检查证明内存操作中的读取时间戳是正确的。
7. 通过 Spartan 证明 R1CS 的正确性。
8. 证明协议过程中使用的所有打开承诺。
9. 将所有证明与承诺和程序 I/O 一起发送给验证者。

验证

根据证明者的证明、承诺和程序 I/O，验证者执行以下操作：

1. 验证字节码内存检查证明
2. 从主 sumcheck 和内存检查证明验证指令查找
3. 验证读写内存证明
4. 验证程序 I/O sumcheck 证明
5. 验证时间戳范围检查证明
6. 验证 Spartan 证明
7. 验证承诺的所有打开证明

如果所有这些检查都通过，则验证者可以安全地假定给定的程序 I/O 有效。然后，验证者可以检查给定的程序 I/O 是否与某些语句匹配。

结论

这篇文章探讨了 Jolt 如何证明和验证 VM 执行的正确性。Lasso 查找参数的使用使 Jolt 成为一个非常简单且可扩展的 zkVM，因为我们可以通过简单地更新指令查找中使用的查找表来轻松添加更多 VM 指令。

Jolt 正在积极维护和不断改进，具有许多优化和令人兴奋的功能，你可以在官方存储库中进行探索。

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～