Bionetta：终极客户端ZKML技术概览

Bionetta: 终极客户端 ZKML。技术概述

Rarimo

Dmytro Zakharov, Lasha Antadze, Oleksandr Kurbatov

当前中立网络的安全级别与早期互联网的安全级别相当。当所有大型公司都专注于性能时，AI 安全方面存在巨大差距。我们不能相信模型背后没有数百名低薪工人。我们不能确定模型不会说谎。我们无法验证模型输出。我们不能确定它不会收集（实际上它会）任何关于客户的个人数据，并且不会与任何人分享。

当 AI 扩展世界时，我们需要一种根本不同的方法来运作。我们推出 Bionetta 🌿 -- 一个旨在解决一些安全问题并允许实现以下属性集合的 zkML 框架：

• 可证明性。验证者可以检查模型执行的正确性。

• 零知识。验证者无法提取任何信息，除非该语句是正确的。例如，用户可以扫描他们的脸并创建相似性证明，但不会与验证者共享任何生物识别数据。

• 客户端。我们尽量避免任何数据泄露给受信任的提供商。该框架允许创建模型，其证明计算成本很低。

神经网络到底是什么？

简单解释，神经网络 fff 是一个函数，由大量参数（我们称之为 θ\thetaθ）参数化。神经网络接受输入 $x$ 并输出预测 yyy。形式上，我们将其写为 y=f(x;θ)y=f(x;\theta)y=f(x;θ)。推断过程如下图 图 1所示。

神经网络的高级抽象

例如，考虑线性回归模型，它接受三个输入 x=(x1,x2,x3)x=(x_1,x_2,x_3)x=(x1​,x2​,x3​)。模型 fff 可以由权重 θ=(θ0,θ1,θ2,θ3)\theta=(\theta_0,\theta_1,\theta_2,\theta_3)θ=(θ0​,θ1​,θ2​,θ3​) 参数化，并且函数本身如下所示：

f(x1,x2,x3;θ0,θ1,θ2,θ3)=θ0+θ1x1+θ2x2+θ3x3f(x_1,x_2,x_3;\theta_0,\theta_1,\theta_2,\theta_3)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3f(x1​,x2​,x3​;θ0​,θ1​,θ2​,θ3​)=θ0​+θ1​x1​+θ2​x2​+θ3​x3​

当我们训练模型（又名神经网络）时，我们调整参数 θ0,…,θ3\theta_0,\dots,\theta_3θ0​,…,θ3​ 以最小化所谓的 损失值，该值表示我们的模型在训练数据上的表现有多差。训练之后，我们固定值 θ~0,…,θ~3\widetilde{\theta}_0,\dots,\widetilde{\theta}_3θ0​,…,θ3​, 并且每当我们需要从传入的输入 x1,x2,x3x_1,x_2,x_3x1​,x2​,x3​ 中获取一些信息时，我们只需计算 f(x;θ~)=θ~0+θ~1x1+θ~2x2+θ~3x3。f(x;\widetilde{\theta})=\widetilde{\theta}_0+\widetilde{\theta}_1x_1+\widetilde{\theta}_2x_2+\widetilde{\theta}_3x_3.f(x;θ)=θ0​+θ1​x1​+θ2​x2​+θ3​x3​.

注意。 我们突然决定回忆机器学习理论的原因（虽然“非常”表面）是我们想出的一个关键优化与我们将如何解释参数 θ\thetaθ 密切相关。请记住这一点！

那么，ZK 在哪里？

现在，有了神经网络 f(x;θ) f(x;\theta)f(x;θ)，我们如何将其包装在零知识系统中？更重要的是，我们追求的目标是什么？在 ZKML 中，我们有两种主要用例：

1. 模型参数 是 私有的（架构仍然是公开的！），但 输入 是 公开的。例如，OpenAI 可能想要隐藏其新模型的权重（他们通过这种方式来隐藏），但为了向用户证明这是生成输入的神经网络，他们可能会使用一些现有的 ZKML 框架（例如 EZKL）。

2. 模型参数 是 公开的，但 输入 是 私有的。这是我们主要感兴趣的情况，称为 客户端证明。例如，神经网络可能是一种面部识别系统，而输入是人的照片。

这样，为了实现神经网络电路，我们需要提供两组信号：输入值 x^\widehat{x}x（以专门格式化的方式来适应电路，我们称之为“量化值”，用帽子表示）和量化权重 θ^\widehat{\theta}θ。根据用例，我们要么隐藏 x^ \widehat{x}x，要么隐藏 θ^\widehat{\theta}θ。然后，我们将原始神经网络的所有计算表示在电路 $\widehat{f} $ 内部，以便 y=f(x)y=f(x)y=f(x) 和 y^=f^(x^;θ^)\widehat{y}=\widehat{f}(\widehat{x};\widehat{\theta})y​=f​(x;θ) 表示大致相同的值。就是这样。

如果唯一的目标是检查输出的正确性，我们可以添加另一个公共信号 y^C\widehat{y}_Cy​C​ — 声明的量化输出。然后，电路可以检查 f^(x^;θ^)≈y^C\widehat{f}(\widehat{x};\widehat{\theta}) \approx \widehat{y}_Cf​(x;θ)≈y​C​ 是否成立（例如，通过检查 f^(x^;θ^)\widehat{f}(\widehat{x};\widehat{\theta})f​(x;θ) 和 y^C\widehat{y}_Cy​C​ 之间的距离（范数）是否低于某个小阈值 ε\varepsilonε）。

整个过程如下图 图 2 所示。首先，我们计算神经网络输出 y=f(x;θ)\color{blue}{y}=f(\color{green}{x};\color{blue}{\theta})y=f(x;θ)，量化该值以获得声明的输出 y^\color{blue}{\widehat{y}}y​。然后，给定神经网络电路 $\widehat{f} $ 和量化输入 x^\color{green}{\widehat{x}}x，我们计算 f^(x^;θ^)\widehat{f}(\color{green}{\widehat{x}};\color{blue}{\widehat{\theta}})f​(x;θ)，并在零知识证明者内部断言 y^≈f^(x^;θ^)\color{blue}{\widehat{y}} \approx \widehat{f}(\color{green}{\widehat{x}};\color{blue}{\theta})y​≈f​(x;θ)，从而产生证明 π\color{purple}{\pi}π。最后，用户可以发布 (y,π)(\color{blue}{y},\color{purple}{\pi})(y,π)。

ZKML 系统概述

Bionetta 改进

电路嵌入权重：利用 R1CS

那么 Bionetta 🌿 有什么特别之处呢？正如前面所说，当输入 xxx 是私有的而权重 θ\thetaθ 是公共的时，我们专门针对这种情况，当在 R1CS 系统中实现时，会带来非常简洁的优化技巧。为了看到这个技巧，假设你想要在零知识计算中实现以下简单模型的计算，该模型由单个矩阵向量乘法组成，具有三个元素，输出两个元素（用花哨的术语来说，称为 多维线性回归）：

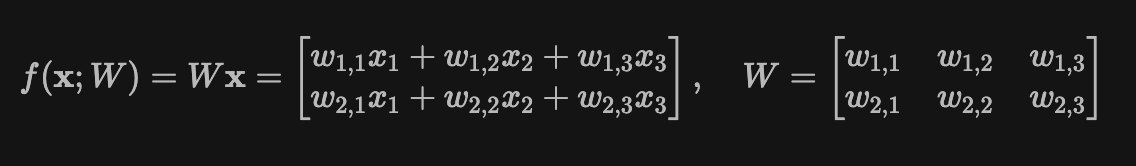
为简单起见，假设所有参数都已正确量化，因此我们正在处理来自某个域的元素。那么，实现函数 f(x;W)f(\mathbf{x};W)f(x;W) 验证所需的门数/约束数是多少？

所有当前方法（包括 EZKL 或 keras2circom）都执行以下操作：我们引入公共权重信号 w1,1,…,w2,3w_{1,1},\dots,w_{2,3}w1,1​,…,w2,3​，私有输入信号 x1,x2,x3x_1,x_2,x_3x1​,x2​,x3​，并计算六个乘积 wi,jxjw_{i,j}x_jwi,j​xj​，其中 i∈{1,2}i\in\{1,2\}i∈{1,2} 且 j∈{1,2,3} j \in \{1,2,3\}j∈{1,2,3}。最后，我们计算相应的总和以获得输出向量元素。Circom 中的示例实现可能如下所示：

template MatVecMul2x3() {
    // 公共输入：大小为 2x3 的权重矩阵 W
    signal input W[2][3];

    // 私有输入：三个输入神经元 x
    signal input x[3];

    // 输出：矩阵向量乘积结果 y=W*x
    signal output y[2];

    for (var i = 0; i < 2; i++) {
        signal sum = 0;
        for (var j = 0; j < 3; j++) {
            sum += W[i][j] * x[j];
        }
        y[i] <== sum;
    }
}

Halo2/PlonK\mathcal{P}\text{lon}\mathcal{K}PlonK 式电路将具有类似的结构。似乎故事结束了，我们已经成功地实现了电路。

🪄 技巧

但是，如果我们告诉你，在 Bionetta 🌿 中，计算这样的 $f(\mathbf{x};W)$ 需要 零约束 呢？这个技巧几乎是显而易见的，并且就在表面上，但我们还没有在 ZKML 丛林中看到它！请看：

所有神经网络权重 不能是信号，而必须作为 常量 嵌入到电路中。这样的构造将节省 大量 信号。

事实上，当在 R1CS 中实现时，任何 乘以常量 和 加法 本质上都是免费的。考虑 f(x;W)=Wxf(\mathbf{x};W)=W\mathbf{x}f(x;W)=Wx 的一般示例，其中权重矩阵 WWW 的大小为 n×mn \times mn×m（因此 x\mathbf{x}x 的大小为 mmm）。

请注意，可能这种优化可能会在 PlonK\mathcal{P}\text{lon}\mathcal{K}PlonK 中以某种方式利用，但直接实现不会产生任何结果：在 $\mathcal{P}\text{lon}\mathcal{K} $ 中乘以常数的加法和乘法仍然需要单独的门，因此无法像在 R1CS 中那样有效地实现。

通过这种方法，经典的机器学习方法（如 线性回归、PCA/LDA 甚至 逻辑回归）的成本 大约为零约束。

坏消息

免费的线性是一件好事，但这里有一些坏消息：非线性激活的数量在现代神经网络中仍然非常多。事实上，例如，考虑最简单的全连接神经网络，它具有单个层：

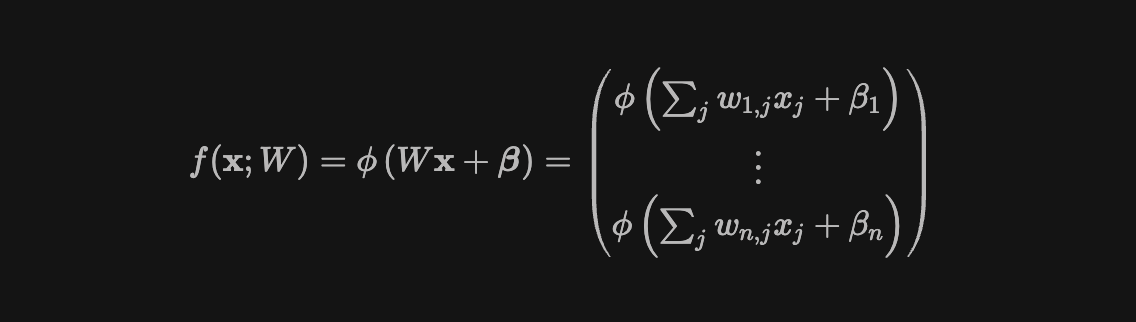
以及此执行的相应图示：

MLP 计算的图示

请注意，这只是之前的矩阵向量乘积示例，但在这里我们只是将非线性函数 $\phi$ 应用于每个输出值。

虽然基于 PlonK\mathcal{P}\text{lon}\mathcal{K}PlonK 的方法可以通过利用查找表来非常有效地处理此类问题，但 vanilla 形式的 R1CS 不具备这种能力。因此，验证 y=ϕ(x)y=\phi(x)y=ϕ(x) 的计算对于最基本的神经网络激活（如 ReLU）需要 每次调用大约 255 个约束（大致对应于素数域的位大小）。例如，在上面的 MLP 中，验证 ϕ(Wx+β)\phi(W\mathbf{x}+\boldsymbol{\beta})ϕ(Wx+β) 的计算对于计算 Wx+βW\mathbf{x}+\boldsymbol{\beta}Wx+β 将花费零约束，但按元素方式应用 ϕ\phiϕ 将添加大约 255n255n255n 个约束。如何解决这个问题？

截至目前，我们提出以下两种解决方案：

1. 构建自定义神经网络架构，该架构使用少量非线性调用，但可以使用高度线性（例如，大型矩阵乘积等）。

2. 为 R1CS 实现自定义查找逻辑。

两种方法都有自己的解决方案，其实现值得撰写博客，因此我们将在此处跳过详细信息，继续前进。

总结

• 我们的框架中的 所有线性运算 都是 免费的。

• 每次非线性调用都会花费 255 个约束。但是，在引入传入的优化技巧之后，此数字将大大减少。

• 如果以特定方式构建神经网络，也就是说，它利用许多线性调用而激活次数相对较少，则我们可以构建高效的电路，这些电路在证明和验证方面都需要极少的资源。

• 尽管如此，我们的基准测试表明，即使在具有大量激活的模型上进行评估，Bionetta 🌿（V1）也比现有方法更快。

有效量化

如何对浮点数执行运算？

现在，之前的讨论完全忽略了我们需要以某种方式处理的不是素数域，而是浮点数/双精度数。换句话说，如果 x,y,zx,y,zx,y,z 被假定为域元素，那么在电路中证明 x×y=zx \times y=zx×y=z 是非常简单的，但是当我们证明 x,y,zx,y,zx,y,z 是任意数字时，我们如何证明 x×y=zx \times y =zx×y=z 这样的语句（比如，0.2×0.3=0.060.2 \times 0.3=0.060.2×0.3=0.06）？

尽管有很多很棒的论文解释了如何证明这样的语句（例如，请参阅 Jens Ernstberger 的 通过精确的浮点 SNARK 实现零知识位置隐私 等人），但我们并没有寻求完美的精度。因此，我们将使用一种标准技术：与其直接乘以 $x \times y $，不如先 量化 它们：也就是说，找到 x^=[2ρx]\widehat{x}=[2^{\rho}x]x=[2ρx] 和 y^=[2ρy]\widehat{y}=[2^{\rho}y]y​=[2ρy]（其中 [⋅][\cdot][⋅] 表示舍入运算），然后找到乘积 z^←x^⋅y^\widehat{z} \gets \widehat{x} \cdot \widehat{y}z←x⋅y​。我们称 ρ\rhoρ 精度系数，它指定我们希望计算达到的精度。但是，问题是如何解释这种乘积的结果：换句话说，我们如何获得 zzz 的值？答案很简单：只需除以 22ρ2^{2\rho}22ρ！也就是说，z≈2−2ρz^z \approx 2^{-2\rho}\widehat{z}z≈2−2ρz。

示例。 假设我们要将 x=0.2x=0.2x=0.2 乘以 y=0.3y=0.3y=0.3。我们选择精度系数 ρ:=10\rho := 10ρ:=10。这样，量化执行如下：x^=[210⋅0.2]=[204.8]=205\widehat{x}=[2^{10}\cdot 0.2]=[204.8]=205x=[210⋅0.2]=[204.8]=205 且 y^=[210⋅0.3]=[307.2]=307\widehat{y}=[2^{10} \cdot 0.3] = [307.2]=307y​=[210⋅0.3]=[307.2]=307。然后，将两个值相乘得到 z^=x^⋅y^=205⋅307=62935\widehat{z}=\widehat{x} \cdot \widehat{y}=205 \cdot 307 = 62935z=x⋅y​=205⋅307=62935。为了获得 zzz 的“真实”值，我们将结果除以 22ρ=2202^{2\rho}=2^{20}22ρ=220，因此我们得到 z≈62935⋅2−20≈0.0600195z \approx 62935 \cdot 2^{-20}\approx 0.0600195z≈62935⋅2−20≈0.0600195。正如人们可能看到的那样，这接近于预期值 0.06。0.06。0.06。

现在，我们需要除以 22ρ2^{2\rho}22ρ 的想法不是随机的：请注意，x^⋅y^\widehat{x} \cdot \widehat{y}x⋅y​ 正好是 [2ρx][2ρy][2^{\rho}x][2^{\rho}y][2ρx][2ρy]，但由于我们期望 2ρx2^{\rho}x2ρx 和 2ρy2^{\rho}y2ρy 都足够大（因为实际上 ρ\rhoρ 大于 20），我们可以放弃向下取整运算：[2ρx][2ρy]≈2ρx⋅2ρy=22ρxy=22ρz[2^{\rho}x][2^{\rho}y] \approx 2^{\rho}x \cdot 2^{\rho}y=2^{2\rho}xy=2^{2\rho}z[2ρx][2ρy]≈2ρx⋅2ρy=22ρxy=22ρz。因此，总而言之，z≈2−2ρx^y^ z \approx 2^{-2\rho}\widehat{x}\widehat{y}z≈2−2ρxy​，如上所述。

如何处理负浮点数？

现在，由于我们需要将数字编码为有限域元素，因此我们需要以某种方式处理负整数。这里的想法很简单：在量化步骤中，如果整数 xxx 为负数，我们只需设置 x^←p+[2ρx]\widehat{x} \gets p+[2^{\rho}x]x←p+[2ρx]。

在这种情况下，为了检查量化值 x^\widehat{x}x 是正数还是负数，通常需要检查它是否落在范围 [0,p−12][0,\frac{p-1}{2}][0,2p−1​] 或 (p−12,p)(\frac{p-1}{2},p)(2p−1​,p) 中，以便我们为正整数和负整数平均分配大约 p2\frac{p}{2}2p​ 个“槽”。在后一种情况下，我们假设整数是正数，而在前一种情况下，我们假设整数是负数。

注意。 但是，我们注意到对 [0,p−12][0,\frac{p-1}{2}][0,2p−1​] 的范围检查有时可能不是最佳选择，因此我们决定将其更改为 [0,2b−1][0,2^{b-1}][0,2b−1]，其中 bbb 是素数域阶 ppp 的位大小。这样，为了检查某个整数的符号，我们只需检查它的 (b−1)(b-1)(b−1)th 位。这仍然不能使我们免于每次范围检查 bbb 个约束，但某些复杂的操作（例如计算 LeakyReLU）可能会更好地优化。

坏消息（再次）

这听起来很棒，但是我们遇到了 keras2circom 一度面临的相同问题。假设我们的目标是计算 f(x)=x10f(x)=x^{10}f(x)=x10，精度系数为 ρ:=35\rho:=35ρ:=35。在这种情况下，如果我们计算量化 x^\widehat{x}x 并将结果计算为 x^10,\widehat{x}^{10},x10，我们将完蛋了：将（大约）35 位的整数乘以 10 次将产生一个 350 位的整数，该整数超过了允许的素数域阶。不用说，这种操作的结果将完全不正确（因为实际上结果将是 x^10,mod;p\widehat{x}^{10},\text{mod};{p}x10,mod;p）。

解决这个问题的一种方法是使用较小的 ρ\rhoρ。例如，设置 ρ:=20\rho:=20ρ:=20 就足够了：在这种情况下，$\widehat{x}^{10} $ 将产生一个（大约）200 位的整数，该整数低于允许的 253 位。但是，如果我们告诉你计算 g(x)=x100g(x)=x^{100}g(x)=x100 呢？你需要设置 ρ:=2\rho:=2ρ:=2（对于 ρ=3\rho=3ρ=3，结果已经具有 300 个精度位），从而导致精度急剧下降。

示例。 为了了解原因，假设我们要在线路中计算 g(0.99)g(0.99)g(0.99)。你将按如下方式进行：你将 x=0.99x=0.99x=0.99 的值量化为 x^←[22⋅0.99]=[3.96]=4\widehat{x} \gets [2^2 \cdot 0.99]=[3.96]=4x←[22⋅0.99]=[3.96]=4。然后，你计算 g(x^)=x^100=4100g(\widehat{x})=\widehat{x}^{100} =4^{100}g(x)=x100=4100 并将结果除以 2100ρ=22002^{100\rho}=2^{200}2100ρ=2200。那么结果是 🥁… 结果是 z=4100/2200=1z =4^{100}/2^{200}=1z=4100/2200=1，而实际结果大约等于 0.366。

为了解决该问题，我们建议在某些中间步骤中简单地削减精度。现在，再次假设我们正在用 ρ=35\rho=35ρ=35 计算 f(x)=x10f(x)=x^{10}f(x)=x10。我们可以将函数执行分解为两个部分：f(x)=x6⋅x4f(x) = \color{blue}{x^6} \cdot \color{green}{x^4}f(x)=x6⋅x4。然后，我们计算量化 x^\widehat{x}x 并计算第一部分：x^6\color{blue}{\widehat{x}^6}x6。如果我们要提取此中间结果的“真实”值，我们将将此结果除以 26ρ=22102^{6\rho}=2^{210}26ρ=2210（请注意，我们在此处没有问题，因为我们有 210 位的精度，远低于允许的 253 位）。但是，我们不打算除以 26ρ2^{6\rho}26ρ，而是除以 25ρ2^{5\rho}25ρ。为什么？因为这样的除法（再次，大约）将对应于此中间结果的量化值。这样，如果我们得到，比如 r^\color{purple}{\widehat{r}}r，我们可以将最终结果计算为 r^⋅x^4\color{purple}{\widehat{r}} \cdot \color{green}{\widehat{x}^4}r⋅x4，这将具有 5ρ=1755\rho=1755ρ=175 位的精度。为了获得最终结果，我们将除以 21752^{175}2175。

示例。 假设我们要在线路中计算 f(0.85)f(0.85)f(0.85) 用 ρ=35\rho=35ρ=35。$x=0.8 $ 的量化产生 x^=0x6cccccccc\widehat{x}=\mathsf{0x6cccccccc}x=0x6cccccccc。然后，我们计算 r^←x^6≫(5ρ)\widehat{r} \gets \widehat{x}^{6} \gg (5\rho)r←x6≫(5ρ)，得到中间结果 r^←0x30466f718\widehat{r} \gets \mathsf{0x30466f718}r←0x30466f718。我们最终将该值乘以 x^4\widehat{x}^4x4 以得到 0x19332e33e75e84b365b56f25da9eaf711fe077c49800\mathsf{0x19332e33e75e84b365b56f25da9eaf711fe077c49800}0x19332e33e75e84b365b56f25da9eaf711fe077c49800。为了将此结果解释回浮点数，我们将此结果除以 25ρ2^{5\rho}25ρ，得到大约 0.196874，这几乎与“真实”值完全吻合。

下图描述了我们算术化方案的整个思想。

所提出的量化的图示。首先，我们将程序拆分为子程序（在我们的例子中，是单独的神经网络层），并且在完成每个子程序后，我们削减输出精度并继续进行。我们重复此操作，直到获得最终结果，该结果可以轻松地反量化

但是，最大的问题是，移位运算在线路内部的计算成本非常高（实际上，这种运算的成本大约为 255 个约束，即素数域的位大小）。我们通过注意到以下几点来解决此问题：

计算 ReLU 然后 削减精度需要 255 个约束，而不是预期的 510 个约束。这是因为 ReLU 和削减精度运算都需要整数的位分解，因此我们可以将它重用于这两种情况。

这样，我们可以在神经网络推理期间应用的每个激活之后自然地削减精度。这样，我们既应用了非线性，又照顾了累积的精度。

实际上，引擎盖下还有更多的技巧（例如，当 α\alphaα 是 2 的负幂时，你可以用大约 256 个约束轻松计算 LeakyReLU 函数 max⁡{x,αx}\max\{x,\alpha x\}max{x,αx} 的执行）。但是，我们将在即将发表的论文中更正式地描述它们。

总结

• 对于足够大的 ρ\rhoρ（实际上，ρ\rhoρ 在 20-35 左右的值就足够了），所提供的量化方案提供了几乎完美的精度。

• 除了精度削减之外，所提供的量化方案没有施加任何其他约束，精度削减可以与非线性调用一起应用。

• 所提出的量化方案允许使用各种现代激活函数：ReLU、LeakyReLU，甚至像 hard sigmoid 或 hard swish 这样的函数，而不会损失 1% 的精度。

示例电路

假设我们要实现一个非常简单的神经网络，该网络基于 28×28 28 \times 2828×28 大小的图像识别数字。因此，我们指定以下神经网络架构：我们将输入神经元扁平化，将它们与 64 个神经元与用作非线性函数的 LeakyReLU（其中 α=132\alpha=\frac{1}{32}α=321​）连接，最后在末尾使用 10 个神经元。简而言之，每个输出神经元将代表模型对相应数字的描绘的置信度（例如，如果输出为 [0,0,0,1.0,0.01,0.2,0,0,0,0][0,0,0,1.0,0.01,0.2,0,0,0,0][0,0,0,1.0,0.01,0.2,0,0,0,0]，这意味着神经网络最确信描绘的数字是 三）。当 Bionetta 🌿 中以 ρ=20\rho=20ρ=20 训练和构建此神经网络时，我们得到以下 Circom 电路：

// 自动生成
pragma circom 2.1.6;

include "./weights.circom";
include "../bionetta-circom/circuits/zkml/includes.circom";
include "../bionetta-circom/circuits/hash/poseidonAny.circom";
include "../bionetta-circom/circuits/matrix/matrix.circom";

template Core(FIELD_BITS) {
    var p = 20;
    signal input image[1][28][28];

    signal input address;
    signal addressSquare <== address * address;

    signal input threshold;

    signal input nonce;
    signal nonceSquare <== nonce * nonce;

    signal input features[10];

    component hash_features = PoseidonAny(10);
    hash_features.inp <== features;
    signal output featuresHash <== hash_features.out;

    component layer1Comp = Flatten(28,28,1,64,get_dense_W(),get_dense_b());
    layer1Comp.inp <== image;

    component layer2Comp = VectorLeakyReLUwithCutPrecision(64,p,2*p,5,FIELD_BITS);
    layer2Comp.inp <== layer1Comp.out;

    component layer3Comp = Dense(64,10,get_dense_1_W(),get_dense_1_b());
    layer3Comp.inp <== layer2Comp.out;

    component lastLayerComp = VectorLeakyReLUwithCutPrecision(10,p,2*p,0,FIELD_BITS);
    lastLayerComp.inp <== layer3Comp.out;

    component verifier = VerifyDist(10, FIELD_BITS);
    verifier.in1 <== lastLayerComp.out;
    verifier.in2 <== features;
    verifier.threshold <== threshold;

    signal output isCompleted <== verifier.out;
}

component main{public [threshold, nonce, address]} = Core(254);

请注意，我们不仅要简单地执行图层逻辑（例如，使用 keras2circom），还要削减精度以处理溢出（例如，请参见 “VectorLeakyReLUwithCutPrecision” 函数）。我们的自动工具可以发现可能发生溢出的地方，因此你在使用 Bionetta 🌿 时可能不会太在意处理精度

请注意，与要求将矩阵和偏差指定为信号相反，我们将它们用作常量，这些常量在文件 “weights.circom” 中进行了硬编码，该文件看起来… 好吧… 就像… 这样…

function get_dense_W(){
    var dense_W[64][784];
    dense_W = [[\
        0xb75d, 0xad2f, 0x2ebd, 0x5e67,\
        0xa981, -0xeaba, -0x60e6, 0x16bc,\
        0x126b, -0x7c81, -0x13ba9, -0xb458,\
        0x11a1, 0x511b, 0xb117, 0x5c92,\
        -0xf179, -0x4855, 0x15a9, -0x10b14,\
        0x2e42, 0x146d, -0x541c,...\
    ]];
    return dense_W;
}

// ...此处指定了无穷无尽的参数...

function get_dense_1_b(){
    var dense_1_b[10];
    dense_1_b = [\
        0x12ff2dc000,0x137ab6e00,0x13d35b2000,\
        0xf43e25000,0xfec98a000,0x14e6c40000,\
        0x125e2fa000,0x144bc40000,\
        0x18c2c4c000,0x12979f8000\
    ];
    return dense_1_b;
} // 喔噢噢，这是最后一个了

现在，为了将输入传递给这个神经网络，我们将输入图像（形式上是形状为 $(28,28,1)$ 且填充了 float32 条目的张量）逐元素乘以 2202^{20}220 并对结果进行四舍五入。例如，假设我传递以下量化图像：

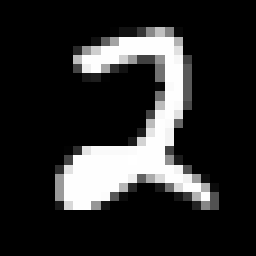
神经网络的示例输入

如果我们检查 witness，这种操作的结果是（为了使符号更小，如果整数超过 22532^{253}2253，我们减去 ppp 以获得“符号感知(sign-aware)”格式）：

为了获得“真实”结果，我们将所有值除以 2202^{20}220：

可以看出，神经网络成功识别出数字并预测为二。事实上，约束的数量略高于 19500：这个数字非常小，可以很容易地被证明和验证。

• 原文链接： mirror.xyz/0x90699B5A52B...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～