3-Slot 最终性:SSF 并非关于“Single” Slot 的共识
- 以太坊中文
- 发布于 2024-11-05 15:23
- 阅读 1070
本文介绍了一种名为3-Slot Finality (3SF) 的协议,旨在在网络延迟有界的情况下,使诚实提议者提出的区块在3个 slot 内完成最终确认。
3-Slot-Finality:SSF 并非关于 “单” Slot
作者:Francesco D’Amato, Roberto Saltini, Thanh-Hai Tran, Luca Zanolini
TL;DR; 在这篇文章中,我们介绍了 3-Slot 最终性(3SF),这是一种协议,旨在当网络延迟被一个已知值 \Delta 限制时,在 3 个 slot 内完成由诚实提议者提出的区块的最终确认——即使后续提议者可能是不诚实的——同时每个 slot 只需要一个投票阶段。这种方法与先前提出的单 Slot 最终性协议形成对比,后者每个 slot 需要三个投票阶段才能在单个 slot 内完成诚实提议区块的最终确认,从而导致更长的 slot 时间。我们还表明,3SF 保证了 SSF 所期望的所有关键属性,提供了一种高效且实用的替代方案,减少了开销,同时确保在几个 slot 内快速且可预测的区块最终确认,以及更短的实际 slot 时间(因为投票阶段实际上比其他阶段花费更长的时间)。因此,与先前提出的协议相比,我们的协议实现了更短的预期确认时间,但代价是区块最终确认的轻微延迟,这延长到了提议三个额外区块所需的时间,而不是在下一个区块提议之前完成最终确认。但是,我们认为对于大多数用户来说,更短的预期确认时间可能就足够了。此外,slot 时间是一个关键参数,会影响链上自动做市商 (AMM) 中由于套利造成的经济泄漏。具体而言,套利利润(以及流动性提供者 (LP) 的损失)与 slot 时间的平方根成正比。因此,减少 slot 时间对于智能合约区块链上的金融应用程序来说非常理想。最后,我们表明我们可以做出进一步的权衡:我们可以将投票阶段的数量增加到两个,而不会影响实际的 slot 长度,并且仅在两个 slot 中实现最终确认。
这篇文章是我们扩展的技术论文的摘要,你可以在这里找到它。
请注意,在这篇文章中,我们将只关注共识协议,暂不讨论验证者集合管理的问题。这方面与有效共识协议的设计无关,可以单独解决。
Single-Slot-Finality,或 SSF,是以太坊共识层的一个备受期待的升级,通常与能够在提议区块的同一 slot 内完成区块的最终确认相关联,这比当前协议在 64 到 95 个 slot 内完成区块的最终确认有了显着改进。这种进步将消除经济安全和更快交易确认之间的权衡。
但是,我们真的需要单 Slot 最终性吗?
要回答这个问题,让我们退一步,问自己另一个问题:当前协议(Gasper)没有保证哪些属性,而我们希望 SSF 能够提供给我们?
- 属性 1. 如果网络延迟低于已知值 \Delta,并且 \geq 2/3 的验证者集合(按权益)是诚实的并且积极参与,那么由诚实节点提议的区块将在短且可预测的时间内完成最终确认。
- 属性 2. 如果网络延迟低于 \Delta,并且 > 1/2 的验证者集合(按权益)是诚实的,即使 < 2/3 的验证者(按权益)积极参与,诚实节点提议的区块将永远不会离开规范链,并且一旦诚实验证者的参与恢复到 \geq 2/3(按权益),那么这样的区块将在短且可预测的时间内完成最终确认。
- 属性 3. 使用上述相同的假设,存在一种_确认_区块的方法,即确定这样的区块是否将始终是规范链的一部分,因此,一旦诚实验证者的参与恢复到 >= 2/3(按权益),它将在短且可预测的时间内完成最终确认。
正如我们所看到的,上面列出的属性都不是关于能够在提议区块的同一 slot 内完成区块的最终确认。但是,可以说,区块越早完成最终确认,就越好。那么,既然我们已经有一个这样的协议(从现在开始,我们将其称为 SSF),它保证了我们上面所有期望的属性,包括能够在同一 slot 内完成区块的最终确认,那么为什么我们不坚持使用单 Slot 最终性呢?
原因是 SSF 每个 slot 需要多个投票阶段。这样做的普遍问题是,由于投票发生时大量数据涌入网络,实际上,每个投票阶段都必须考虑额外的延迟。例如,为了减少整体网络带宽,以太坊目前为每个投票阶段采用签名聚合方案,通过该方案,投票首先发送给聚合器,然后由聚合器分发聚合签名。这意味着投票阶段需要 2\Delta 时间,也就是正常网络延迟的两倍。即使将来发现我们可以取消聚合器,但可以合理地预期投票阶段比其他阶段花费更长的时间。在本节的其余部分中,我们假设根据当前的以太坊协议,一个投票阶段持续 2\Delta。
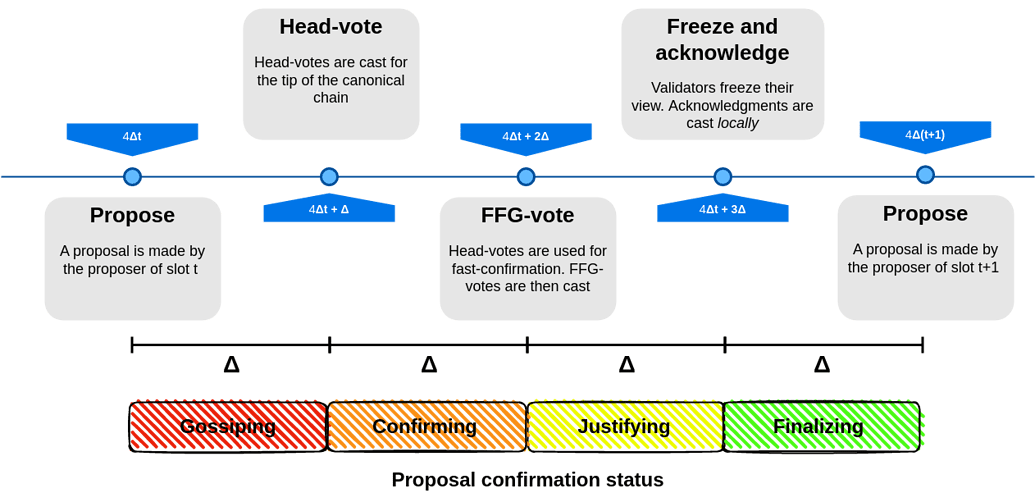
因此,投票阶段越多,区块时间往往就越长。具体来说,正如稍后详细说明的那样,SSF 将每个 slot 分为 4 个阶段:(1) 区块提议,(2) Head-vot 投票,(3) FFG-vot 投票,以及 (4) Acknowledgment 确认投票加上视图冻结(对于这里的论点来说,视图冻结并不重要)。阶段 (3) 和 (4) 必须分别等待阶段 (2) 和 (3) 完成。但是,下一个 slot 及其任何阶段的开始_不_依赖于阶段 (4)。因此,SSF 中的 slot 长度为 \Delta + 2\Delta + 2\Delta + \Delta = 6 \Delta。
在我们的协议 (3SF) 中,slot 也由 4 个阶段组成,但其中只有一个是投票阶段。具体来说,我们有 (1) 区块提议,(2) Head/FFG-vot 投票,其中同时进行 Head-vote 投票和 FFG-vote 投票,(3) 快速确认,以及 (4) 视图合并。然后,slot 长度变为 \Delta + 2\Delta + \Delta + \Delta = 5\Delta。
首先,区块时间已被证明是决定链上 AMM 中_经济泄漏_到套利的重要参数。例如,套利利润(以及流动性提供者 (LP) 的损失)与区块时间的平方根成正比,因此智能合约区块链上构建的金融应用程序非常希望降低区块时间。
其次,通过更短的区块时间,我们可以实现更短的预期确认时间,这是指从用户提交交易到该交易被确认(即包含在已确认区块中)的预期延迟。这对应于确认由诚实提议者提议的区块所需的时间 + \frac{(1+\beta) \cdot \text{slot-time}}{2(1 - \beta)},其中 \beta 表示网络中的对抗能力。在 3SF 和 SSF 中,确认由诚实验证者提议的区块所需的时间均为 3\Delta。因此,对于 \beta = \frac{1}{3},SSF 的预期确认时间为 9\Delta,而我们的协议为 8\Delta,这意味着 \approx 11\% 的改进。对于 \beta = 0,SSF 的预期确认时间为 6\Delta,而我们的协议为 5.5\Delta,这意味着 \approx 8\% 的改进。
但是,正如人们所期望的那样,虽然 3SF 的预期确认时间更短,但预期最终确认时间(即完成交易的预期时间)更长。预期最终确认时间的计算方式与预期确认时间类似,即完成由诚实提议者提议的区块所需的时间 + \frac{(1+\beta) \cdot \text{slot-time}}{2(1 - \beta)}。在 SSF 中,完成一个诚实区块需要 5\Delta,在 3SF 中需要 11\Delta,而 3SF 的双 slot 变体需要 8\Delta。因此,对于 \beta = \frac{1}{3},SSF 的预期最终确认时间为 11\Delta,3SF 为 16\Delta,而 3SF 的双 slot 变体为 13\Delta,这意味着 3SF 的预期最终确认时间比 SSF 的高 \approx 46\%,但对于其双 slot 变体,这降至 \approx 18\%。对于 \beta = 0,SSF 的预期最终确认时间为 8\Delta,3SF 为 13.5\Delta,而 3SF 的双 slot 变体为 10.5\Delta,这意味着 3SF 的预期最终确认时间比 SSF 的高 \approx 69\%,但对于其双 slot 变体,这降至 \approx 31\%。
总的来说,3SF 通过以更高的预期最终确认时间来换取更短的预期确认时间来实现平衡,这对于大多数用户来说可能就足够了。同时,它提供了更短的 slot 时间。作为额外的优势,3SF 的 slot 结构更接近当前以太坊的 slot 结构。
一篇之前的研究文章已经强调了 3SF 中投票阶段数量的问题,并提出了一个解决方案。但是,只有当后续两个 slot 中的提议者也是诚实的,此解决方案才能保证所需的属性。
通过将协议减少到每个 slot 仅一个投票阶段,这朝着正确的方向迈出了一步,但它也引入了一个缺点:满足最终确认所需条件的较低概率。但是,我们现在表明,可以设计一种协议,该协议可以将投票阶段的数量减少到一个,而无需后续 slot 中的提议者是诚实的。
回顾 SSF 协议
我们以 SSF 协议为起点构建我们的 3SF 协议,该协议总结在下图中。
现在让我们回顾一些最重要的概念。
(但是,建议读者阅读原始帖子)。
- 涨落结构。 SSF 由两个子协议组成。第一个是PBFT 样式(名称来自这篇开创性论文)子协议,即使在网络分区的情况下,它始终确保安全,但至少需要 2/3 的诚实权益。第二个是动态可用 (DA) 子协议,即使某些诚实验证者停止参与,它也能保证进度,前提是简单的诚实多数。结合这两种类型的子协议的协议称为涨落协议。
- 基于 Casper 的 BFT 子协议。 PBFT 样式的子协议主要基于 Casper,这是 Gasper 当前使用的最终性工具。与 Gasper 相比,在 SSF 中,检查点是区块和 slot 的对,而不是区块和纪元的对。这是因为,在 SSF 中,在某种意义上,纪元和 slot 是同一件事。但是,_检查点证明和最终确认的一般规则是相同的。让我们简要回顾一下这些规则。首先,区块最终确认是通过检查点最终确认来实现的。具体来说,要最终确认区块 B,我们需要最终确认某个检查点 (B_\mathsf{d},s),其中 B_\mathsf{d} 是 B 的后代,并且 s \geq \mathsf{slot}(B\\mathsf{d})。其次,检查点最终确认分两个阶段完成:首先检查点被证明,然后被证明的检查点被最终确认。现在让我们解释一下这个过程是如何运作的。根据定义,创世检查点 (B_\mathsf{genesis},0) 既被证明也被最终确认。任何其他检查点的证明和最终确认都是通过
FFG-vote投票来实现的,这些投票是检查点之间链接的投票。它们的形式为 C_\mathsf{s} \to C_\mathsf{t},其中 C_\mathsf{s} 和 C_\mathsf{t} 分别称为_源_和_目标检查点。如果存在来自 \geq 2/3 的验证者(按权益加权)的FFG-vote投票,用于链接 C_\mathsf{s} \to (B,s),其中 C\\mathsf{s} 是经过证明的检查点,则检查点 (B,s) 被证明。然后,如果 (B,s) 被证明,并且存在来自 \geq 2/3 的验证者(按权益加权)的FFG-vote投票,用于链接 (B,s) \to (B',s+1),其中 B' 是 B 的后代,则检查点 (B,s) 被最终确认。除此之外,为了能够在单个 slot 内最终确认区块,SSF 引入了Acknowledgment确认投票 ((B,s),s),粗略地说,这是一种“压缩”的FFG-vote投票,表示验证者看到了一个给定的检查点 (B,s) 在 slot s 结束时被证明。任何看到检查点 (B,s) 被证明并收到来自 \geq 2/3 的验证者(按权益加权)的Acknowledgment确认投票 ((B,s),s) 的人都可以安全地认为检查点 (B,s) 已被最终确认。 - RLMD-GHOST 作为 DA 子协议。 SSF 利用 RLMD-GHOST 作为 DA 子协议来实现上述属性 2 和 3。在 RLMD-GHOST 中,验证者对区块进行投票。我们使用术语
Head-vote投票来指代此类投票。RLMD-GHOST 在 睡眠模型 中工作,其中验证者可能会_睡着_并停止参与一段时间。RLMD-GHOST 的一个关键属性是,只要网络延迟小于 \Delta,并且少于 1/2 的验证者(按权益加权)是不诚实的,那么由诚实提议者提议的区块将收到并继续收到所有活跃验证者的Head-vote投票。重要的是,RLMD-GHOST 带有以下_确认_规则,该规则允许确定区块是否被确认,也就是说,它将始终是任何诚实验证者的规范链的一部分:相对于当前规范链来说,任何至少 \kappa 深度的区块都被确认(规范链的头部为 0 深度,其父级为 1 深度,依此类推)。我们将此规则称为\kappa-深度确认规则。值 \kappa 表示我们需要多少个 slot 才能确定(除了可以忽略不计的概率之外)这些 slot 中的至少一个提议者是诚实的。显然,这意味着 \kappa >> 1。 - 快速确认。 与 \kappa-深度确认规则相比,快速确认允许在提议区块的同一 slot 内_确认_区块。但是,它要求至少 2/3 的验证者(按权益加权)是诚实的并且活跃。当在从发送时间开始延迟 \Delta 后收到来自所有活跃验证者的超过 2/3 的
Head-vote投票(按权益加权)时,就会发生区块的快速确认。在上图中,Head-vote投票在 4$\Delta s$ + \Delta 时进行,这意味着它们在 slot s 中的 \Delta 时间内发送。如果在 4$\Delta s + 2\Delta$ 时一个诚实验证者收到针对特定区块 B 的超过 2/3 的Head-votes投票(按权益加权),则 B 被认为是_快速确认_的。 - BFT 和 DA 协议之间的集成。 在 SSF 中,诚实验证者确定要进行的
FFG-vote投票,如下所示。源检查点对应于他们在视图中的最大证明检查点,这是具有最高 slot 的证明检查点(除非 > 1/3 的权益被削减,否则同一 slot 的两个不同证明检查点永远无法被证明)。目标检查点的 slot 对应于当前 slot,而区块对应于由 DA 协议快速确认的区块(如果存在),或者否则对应于由 DA 协议通过 \kappa-深度确认规则确认的最高区块。 - 长度为 4\Delta 的 Slot。 除非另有说明,为了与之前的文献保持一致,在本帖子的其余部分中,我们假设投票阶段仅花费 \Delta 时间,也就是说,我们没有明确考虑由投票阶段引入的额外延迟。那么,在 SSF 中,每个 slot 的长度为 4\Delta。
构建我们的 3SF 协议
我们现在开始构建我们的 3SF 协议,方法是采用 SSF 协议并应用以下修改,以便每个 slot 只有一个投票阶段。
FFG-vote投票与Head-vote投票在进入 slot 的 \Delta 时间进行,其中 \Delta 表示网络延迟。- 删除快速确认。
因此,FFG-vote 投票的目标是由 DA 协议确认的最长链。在这种情况下,DA 协议确保如果提议者是诚实的,则所有诚实验证者都会看到与 DA 协议确认的相同的链。
- 没有
Acknowledgment确认投票。
通过删除一个阶段,slot 的长度将减小到 3\Delta。由此产生的协议可以示意如下。
现在让我们看一下即使在简化的假设下,即我们有两个连续的诚实提议者,以及通常的假设 (i) < 1/3 的验证者(按权益加权)是不诚实的,并且 (ii) 网络延迟小于 \Delta,这样的协议会如何运行。
- slot s 中的提议者提议区块 B。
- 由于 DA 协议的属性,slot s 中的所有诚实验证者都对 B 进行
Head-vote投票。但是,鉴于 B 刚刚被提议,B 也不能成为 DA 协议确认的链的一部分。这意味着诚实验证者发送的FFG-vote投票的目标是 B 的严格祖先。所有验证者对 DA 协议确认的链都有相同的看法。这意味着他们都发送具有相同目标 (B_\mathsf{a},s) 的FFG-vote投票,其中 B_\mathsf{a} 是 B 的祖先。(从现在开始,让我们使用符号 B_\mathsf{a} \preceq B 来表示 B_\mathsf{a} 是 B 的非严格祖先,而 B_\mathsf{a} \prec B 来表示它是严格祖先,也就是说,B_\mathsf{a} \preceq B 表示 B_\mathsf{a} \prec B 或 B_\mathsf{a} = B.) - slot s+1 中的提议者提议区块 B',它是 B 的子区块,并将 slot s 中发送的所有
FFG-vote投票打包到其中。 - 然后,在 slot s+1 中投票的验证者将 (B_\mathsf{a},s) 视为已证明。这意味着他们进行
FFG-vote(B_\mathsf{a},s) \to (B'_\mathsf{a},s+1)(我们使用符号 C_\mathsf{s} \to C_\mathsf{t} 来表示具有源 C_\mathsf{s} 和目标 C_\mathsf{t} 的FFG-vote投票),其中 B'_\mathsf{a} \prec B'。但是,鉴于我们已经放弃了快速确认,DA 协议仅通过 \kappa-深度确认规则进行确认。鉴于 \kappa > 1,这意味着 B'_\mathsf{a} \prec B。因此,我们最多只能证明 B 的严格祖先,而不是 B,通过在此 slot 中发送的投票,这使得在下一个 slot 中最终确认 B 变得不可能。
以上表明我们确实需要快速确认。因此,让我们将它们重新引入刚刚提出的协议中。具体来说,对于 FFG-vote 投票,我们使用前一个 slot 中快速确认的链,而不是当前 slot 中的链来确定目标区块。这是因为,鉴于 Head-vote 投票和 FFG-vote 投票是同时进行的,显然我们不能使用在给定 slot 进行的 Head-vote 投票来确定在同一 slot 中进行的 FFG-vote 投票的目标。我们只需要等待来自投票时间的 \Delta 来执行快速确认。结果是,我们回到了长度为 4\Delta 的 slot,如下图所示,该图说明了最后一个协议。
现在让我们看看这是否可行。
- 在 slot s 中,由诚实验证者进行的
FFG-vote投票的目标检查点中的区块要么是由 DA 协议确认的链(通过上述 \kappa-深度规则),要么是在前一个 slot 中快速确认的链。事实证明这是一个问题,因为一些验证者可能在前一个 slot 中快速确认了一个区块 B^{\mathsf{fastconf}},而另一些验证者可能没有。因此,很可能一些验证者进行以目标区块 B^{\mathsf{conf}} 的FFG-vote投票,另一些验证者进行以目标区块 B^{\mathsf{fastconf}}_\mathsf{a} 的FFG-vote投票。问题是,即使 B^{\mathsf{conf}}_\mathsf{a} \prec B^{\mathsf{fastconf}},通过使用 SSF/Gasper 的证明规则,这会导致我们不证明 slot s 的任何检查点,这似乎是倒退而不是前进。
我们如何解决这个问题?
请注意,当我们通过区块 B 最终确认检查点时,我们最终确认整个链,而不仅仅是 B。我们可以对已证明的检查点执行相同的操作。也就是说,如果我们证明了 (B,s),我们还会将任何检查点 (B_\mathsf{a},s)(其中 B_\mathsf{a} \preceq B)视为已证明。但是,这不足以解决从最后一个示例中高亮显示的问题,因为不同的验证者可能会对不同的检查点进行 FFG-vote 投票,即使包含在此类检查点中的区块位于同一链上。
我们需要更进一步:
如果源检查点 (B_\mathsf{s},s_\mathsf{s}) 已被证明,则
FFG-vote(B_\mathsf{s},s_\mathsf{s}) \to(B_\mathsf{t},s_\mathsf{t}) 被认为有助于证明任何检查点 (B',s_\mathsf{t}) 的合理性,其中 B_\mathsf{s}\preceq B' \preceq B_\mathsf{t},也就是说,B’ 是 B_\mathsf{s} 和 B_\mathsf{t}(包括在内)之间的任何区块。请注意,目标检查点和已证明检查点中的 slot 是相同的。如果我们有来自 \geq 2/3 的验证者(按权益加权)的
FFG-vote投票有助于证明 (B',s_\mathsf{t}) 的合理性,则 (B',s_\mathsf{t}) 被认为是已证明的。
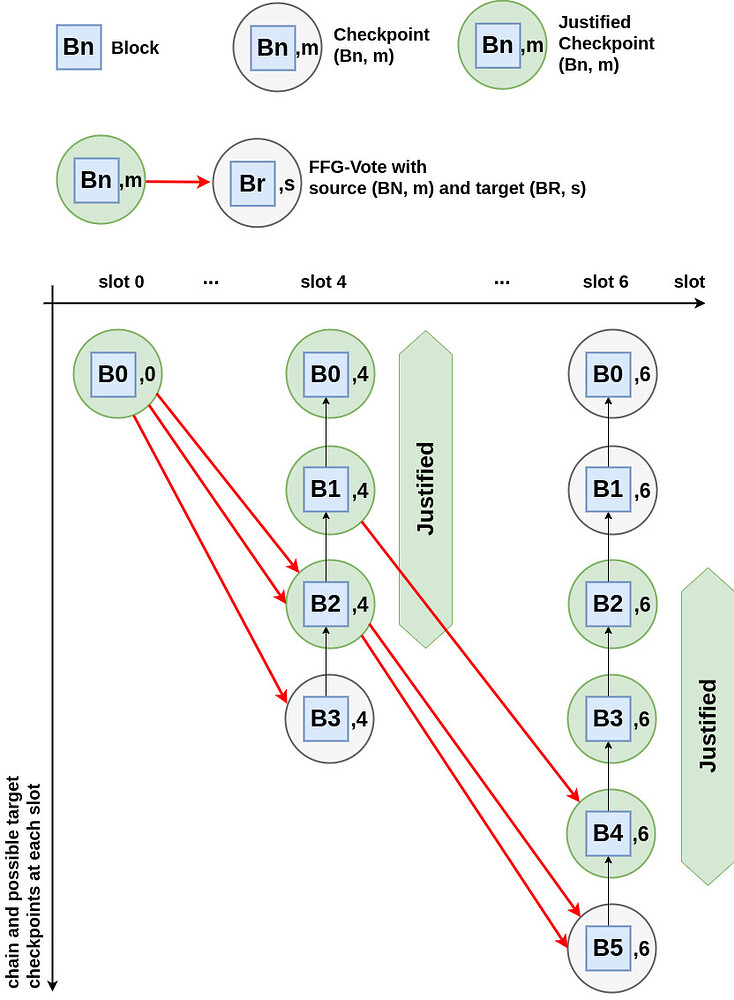
在继续之前,让我们回顾一下下面的示例,以确保这个新的证明规则是明确的。我们考虑 3 个 slot:slot 0、4 和 6。对于每个 slot(例如 s),下图显示了在 slot s 中投出的 FFG-vote 投票的可能目标检查点的列表。这包括所有检查点,这些检查点包含截至 slot s 中的投票时间收到的任何区块(除了在 slot s 中提议的区块,该区块与 slot s 配对)。
 \
justification2833×1133 144 KB
\
justification2833×1133 144 KB
我们假设只有 4 个验证者,所有验证者都具有相同的权益。
让我们首先考虑 (B0,0) 和 slot 4 的检查点之间的 FFG-vote 投票。如果我们取 B,使得 B0 \preceq B \preceq B2,那么我们有 3 \geq \frac{2}{3} 4 个 (B0,0) 和检查点 (B_\mathsf{d},4) 之间的 FFG-vote 投票,使得 B \preceq B_\mathsf{d}。
鉴于 B0 \preceq B,按照我们的规则,(B0,4)、(B1,4) 和 (B2,4) 被证明。但是,(B3,4) 未被证明,因为只有 FFG-vote(B0,0) \to (B3,4) 支持其合理性。
现在我们转到 slot 4 的检查点和 slot 6 的检查点之间的 FFG-vote 投票。请注意,通过上面的推理,所有这些 FFG-vote 投票都具有已证明的检查点,作为源。现在,取 B,使得 B2 \preceq B \preceq B4。请注意,我们有 3 个来自已证明的检查点 (B_\mathsf{a},4) 和检查点 (B_\mathsf{d}.6) 之间的 FFG-vote 投票,使得 B_\mathsf{a}\preceq B\preceq B_\mathsf{d}。按照我们的规则,这意味着 (B2,6)、(B3,6) 和 (B4,6) 被证明。重要的是,尽管 (B0,4) 和 (B1,4) 被证明,但 (B0,6) 和 (B1,6) 未被证明。对于 (B1,6),这是因为我们只有两个 FFG-vote 投票 (B1,4) \to (B4,6) 支持其合理性。然而,对于 (B0,6),我们没有 FFG-vote 投票支持其合理性。
这个新规则显然允许给定的 slot 拥有多个已证明的检查点。没关系,因为它们会在同一条链上。但是,当计算最佳证明检查点时,仅使用检查点 slot 就不再足够了。然后,我们自然地定义在具有相同 slot 编号的检查点之间的排序,根据区块提议的 slot 进行排序,以便如果 \mathsf{slot}(B) < \mathsf{slot}(B'),那么 (\mathsf{slot}(B'),s) 大于 (\mathsf{slot}(B),s)。
然后,让我们使用这个新的协议恢复之前的示例,假设只有 slot s 的提议者是诚实的(除了通常的假设):
- 在 slot s 中,任何诚实验证者都进行
FFG-voteC_\mathsf{s} = (B_{\mathsf{aa}},s') \to C_d = (B_\mathsf{a},s),其中 C_\mathsf{s} 和 C_d 对于每个验证者可能不同,但具有 B_\mathsf{aa} \preceq B_\mathsf{a} \prec B 的属性。然后,这组FFG-vote投票至少会导致证明一个检查点 (B_\mathsf{j},s),其中 B_\mathsf{j} \prec B。
此外,所有诚实验证者都快速确认 B。
- slot s+1 的提议者可以提议他们想要的任何东西,或者什么都不提议。
- 在 slot s+1 中,任何诚实验证者都进行
FFG-vote(B_\mathsf{j},s) \to (B,s+1),其中 B_\mathsf{j} 对于每个验证者可能不同,但 B_\mathsf{j} \prec B。这是因为,从上面的要点中,我们知道 slot s 至少有一个已证明的检查点。总的来说,这意味着这组FFG-vote投票证明了 (B,s+1) 的合理性。到目前为止一切都好!看起来我们正朝着正确的方向前进! - slot s+2 的提议者可以提议他们想要的任何东西,或者什么都不提议。
- 鉴于我们在上面建立的检查点排序规则,任何诚实验证者都将 (B,s+1) 视为最大的已证明检查点。然后,任何诚实验证者都进行
FFG-vote(B,s+1) \to (B'',s+2),其中 B'' 对于每个验证者可能不同,但由于 DA 协议的属性,B \prec B''。使用 Gasper/SSF 最终确认规则,这不一定会产生最终确认 (B,s+1)。但是,这可以很容易地修复。让我们看看如何操作!
请注意,在 Gasper/SSF 中,在 FFG-vote(B,s+1) \to (B',s+2) 中,区块 B' 不携带任何关于最终确认 (B, s+1) 是否安全的有意义的信息。这样的投票表示签署它的验证者在 slot s+2 中投票时看到了 (B,s+1) 作为最大的已证明检查点(这正是 SSF 协议中 Acknowledgment 确认投票所做的事情)。因此,如果在稍后的 slot(即在 slot > s + 2 中),它签署了一个以低于 (B,s+1) 的检查点为源的 FFG-vote 投票,则该验证者将被削减。这意味着我们可以按如下方式修改最终确认规则。
如果我们有 \geq 2/3 的验证者(按权益加权)进行 FFG-voting (B,s+1) \to (B',s+2),其中 B' 对于每个验证者可能不同,但使得 B \preceq B',那么 (B,s+1) 被最终确认。
通过这个最后的修改,在上面的第 6 步中,我们最终确认了区块 B,正如我们希望做的那样!
这个协议安全吗?
好问题!为了使这个协议安全,我们只需要稍微修改削减规则。
让我们首先回顾一下 Gasper 采用的削减规则,这些规则与 SSF 使用的规则相同(准确地说,SSF 有一个额外的规则用于 Acknowledgment 确认投票,但我们可以忽略它,因为我们不使用那种类型的投票)。
首先,如果一个验证者发送了两个不同的 FFG-vote 投票,但具有相同 slot 的目标检查点,则该验证者将被削减。
其次,如果一个验证者发送了两个 FFG-vote 投票 (*,\mathit{s1}_\mathsf{s})\to(*,\mathit{s1}_\mathsf{t}) 和 (*,\mathit{s2}_\mathsf{s})\to(*,\mathit{s2}_\mathsf{t}) 使得 \mathit{s1}_\mathsf{s} < \mathit{s2}_\mathsf{s} 并且 \mathit{s2}_\mathsf{t} < \mathit{s1}_\mathsf{t},则该验证者将被削减。这被称为环绕投票,因为第一个投票环绕了第二个投票。
Gasper/SSF 确保如果两个冲突的区块被最终确认,那么我们可以削减至少 1/3 的验证者集合。
现在我们表明,以上两个规则对于 3SF 来说是不够的。
请注意,在 Gasper/SSF 中,验证者进行两个源自同一 slot 的检查点的 FFG-vote 投票是完全合法的。这是可以的,因为 Gasper/SSF 确保对于同一 slot,永远不会证明两个不同的检查点(除非 > 1/3 的验证者(按权益加权)不诚实)。但是,使用我们修改的协议,情况不再如此 。这意味着在我们的协议中,目前可以进行两个 FFG-vote 投票 (B,s) \to (B_d,s+1) 和 (B_\mathsf{a},s) \to (B',s+2),其中 (B,s) 和 (B_\mathsf{a},s) 都被证明,且 B_\mathsf{a} \preceq B,且 B' 与 B_d 冲突。这意味着第一个 FFG-vote 投票可以帮助最终确认检查点 (B,s),而第二个投票可以帮助证明更高但冲突的检查点 (B',s+2) 的合理性,然后可以从中最终确认这样一个检查点,而不会犯下任何可削减的罪行。
幸运的是,解决这个问题的方法很简单。我们使用以下规则扩展 Gasper/FFG 削减规则。
两个
FFG-vote$(\mathit{B1},s) \to (*,\mathit{s1}_\mathsf{t})$ 和 $(\mathit{B2},s) \to (*,\mathit{s2}_\mathsf{t})$,其中 $\mathsf{slot}(\mathit{B1}) < \mathsf{slot}(\mathit{B2})$ 且 $\mathit{s2}_\mathsf{t} < \mathit{s1}_\mathsf{t}$ 构成一种可惩罚的违规行为(环绕投票)。
正如我们所见,通过此规则,可以防止上述情况的发生。
实现注意事项
新引入的惩罚规则需要访问区块的 slot number。这带来了一个小问题,因为 checkpoint FFG-vote s 不包括完整的区块,而只包括哈希值,我们需要仅通过查看验证者发出的 FFG-vote s 来确定验证者的可惩罚性,而无需收到通过其哈希值引用的实际区块。
通过将 checkpoint 扩展为三元组 (H,s,p) 而不是仅元组 (H,s) 就可以轻松解决此问题,其中 H 是区块的哈希 (例如 B),s 是 checkpoint 的 slot,p 是 B 的 block slot,即,p = $\mathsf{slot}(B)$。当然,这也意味着在接受 FFG-vote(H,s,p) $\to$ C_\mathsf{t} 作为有效并将其计入 justifications/finalizations 之前,我们需要检查 B.\mathsf{slot}=p,其中 B 是具有哈希 H 的区块。
其他属性呢?
到目前为止,我们只解决了我们感兴趣的第一个属性:如果网络延迟低于 $\Delta$ 且 >= 2/3 的验证者集(按 stake)是诚实并积极参与的,那么由诚实节点提议的区块将在短时间内且可预测的时间内完成 finalization。
那么我们在开头列出的其他两个属性呢?
这些属性已通过 SSF 采用的 DA 协议(即 RLMD-GHOST)保证。因此,我们可以使用 RLMD-GHOST 作为我们的 DA 协议,也可以使用另一个 DA 协议,例如 TOB-SVD。
在 我们的扩展技术报告 中,我们详细展示了如何按照我们刚刚介绍的描述使用 RLMD-GHOST 和 TOB-SVD 来实现 3-Single-Slot Finality。
我们可以做得比 3-Slot-Finality 更好吗?
事实证明,通过重新引入 Acknowledgment 投票,我们实际上可以将 finalization 减少到仅两个 slot。
当然,这意味着每个 slot 有两个投票阶段,而不是一个,但是,如上所述,这不会影响实际的 slot length(也就是说,当我们考虑投票阶段所需的额外延迟时),因为 Acknowledgment 投票的分配可以与任何后续阶段并行进行。
在 3SF 中,Acknowledgment 投票将在快速确认时间进行,即 slot 中的 2$\Delta$。
与 SSF 协议中一样,为了确保安全,我们需要添加以下惩罚规则。
一个
FFG-vote(\mathit{B1},s1_\mathsf{s}) \to (*,s1_\mathsf{t}) 和一个Acknowledgment投票 ((\mathit{B2},\mathit{sa}),\mathit{sa}),其中 $\mathit{sa} < s1_\mathsf{t}$ 并且 s1_\mathsf{s} < $\mathit{sa}$,或者 s1_\mathsf{s} = $\mathit{sa}$ 且 $\mathsf{slot}(\mathit{B1}) < \mathsf{slot}(\mathit{B2})$ 构成一种可惩罚的违规行为。
- Towards Attester-Includer Separation
- Three-Tier staking (3TS) - Unbundling Attesters, Includers and Execution Proposers
- Paths to SSF revisited
- 原文链接: ethresear.ch/t/3-slot-fi...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 翻译
- 学分: 0
- 分类: 以太坊
- 标签: Single-Slot Finality 3-Slot Finality 以太坊 共识协议 区块确认 RLMD-GHOST
- 以太坊应该停止担心扩展性,去做人们想要的东西 134 浏览
- Vitalik的L2重置:以太坊为何需要此航向修正 53 浏览
- 如何桥接到MegaETH(今天测试网,主网即将上线) 199 浏览
- Vitalik: 重新评估以太坊 Layer2 147 浏览
- lambdaworks 2026 年更新路线图和优先级 220 浏览
- BFT共识中的乐观单轮投票最终性 162 浏览
- Gloas注解:分叉选择 120 浏览
- Hegotá应完成审查阻力的圣三位一体 256 浏览
- Hegató Headliner 提案:FOCIL,EIP-7805 - 魔术师 / 原始汤 284 浏览
- Hegotá 头条提案:FOCIL,EIP-7805 - 魔法师 / 原始汤 244 浏览
- Hegató Headliner 提案:FOCIL,EIP-7805 - 魔法师/原始汤 296 浏览
- Gloas 注解:信标链 76 浏览
 \
SSF1035×492 44 KB
\
SSF1035×492 44 KB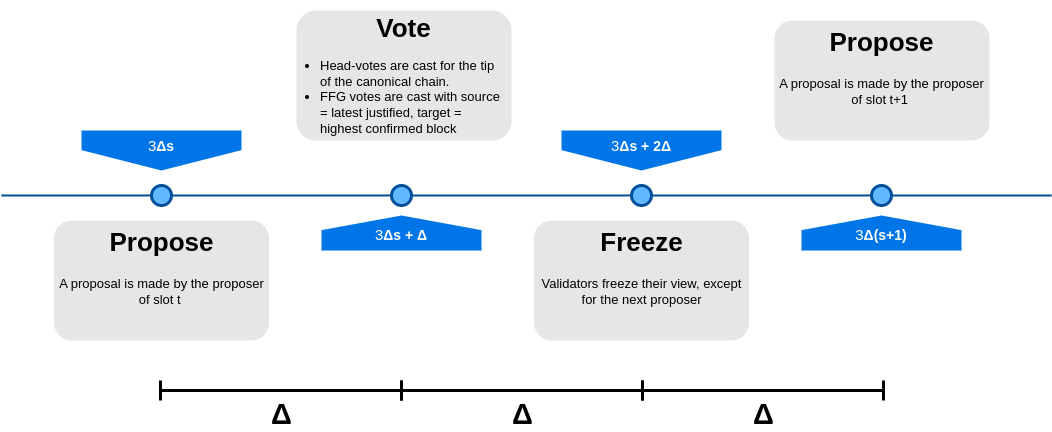 \
attempt11052×432 30 KB
\
attempt11052×432 30 KB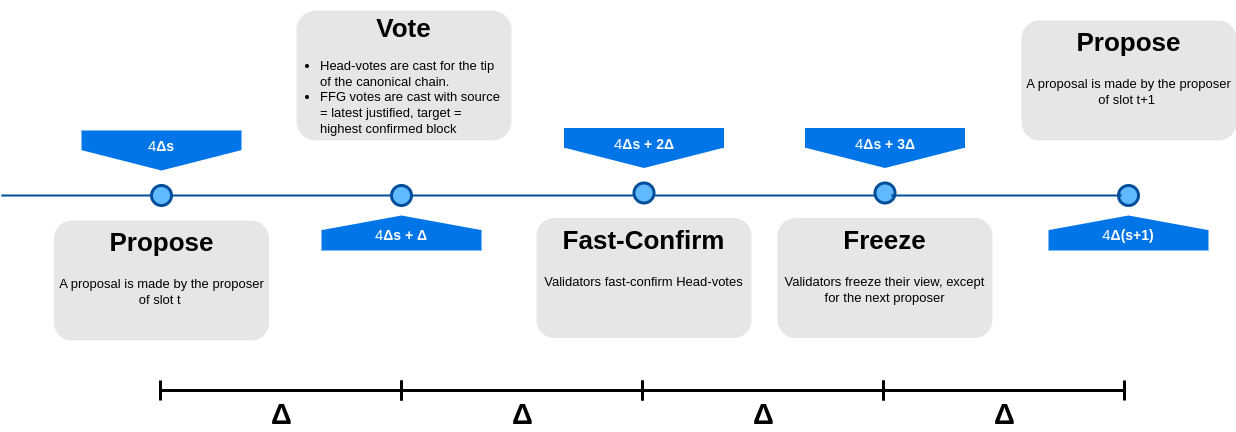 \
attempt21236×432 34.2 KB
\
attempt21236×432 34.2 KB
