配对密码之美：聚合签名和阈值签名

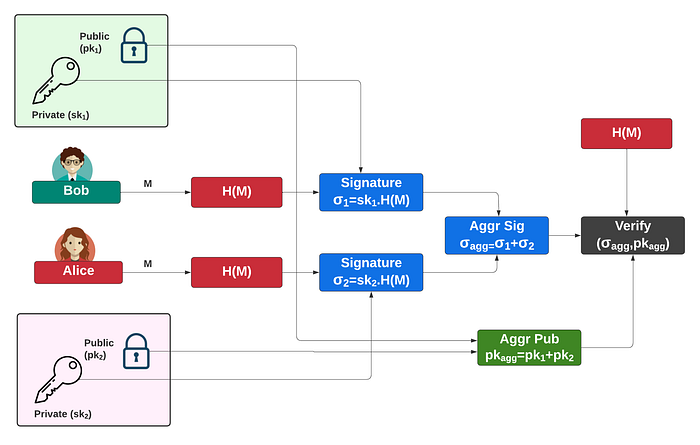
基于配对密码学的魅力：聚合签名和门限签名

我知道椭圆曲线密码学（ECC）面临来自量子计算机的风险，但它在过去几十年里保护着我们，其纯粹的美丽和力量是不可否认的。事实上，没有它们，我们就不会有区块链技术。对我来说，基于配对的密码学是最优雅的，尤其是在它能实现的魔法方面。在这种情况下，我们将汇集多个签名，然后将它们组合起来创建一个单一签名，而不会增加最终签名的整体大小，然后创建一个聚合公钥来验证签名。简直是密码学的魔法！

总的来说，描述配对的工作原理并不容易，但基本上，我们有许多由以下公式定义的点：

$y^2 = x^3 + ax + b \pmod{p}$

其中 $p$ 是一个素数，而 $a$ 和 $b$ 是我们为曲线选择的常数值。如果选择正确的值，我们可以得到一个组（G1 和 G2）中的两组点。之后，我们可以定义这些组上点（g1 和 g2）之间的配对（e()）：

e(g1, g2)

然后配对具有有趣的属性：

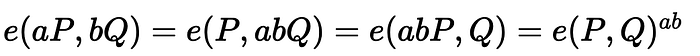
其中 a 和 b 在这种情况下是标量值，而 P 和 Q 是各个组中的点。

签名

Boneh–Lynn–Shacham (BLS) 签名方法。它使用带有椭圆曲线群的双线性配对，并提供一些针对索引微积分攻击的保护。BLS 还可以生成短签名，并且已被证明是安全的。虽然 Schnorr 需要随机数来生成多个签名者，但 BLS 并不依赖这些。

如果 Alice 想要创建 BLS 签名，她首先生成她的私钥 ($sk$)，然后取椭圆曲线上的一个点 ($G$) 并计算她的公钥 ($pk$)：

$P = sk \cdot G$

其中 $G$ 是 $G2$ 上的基点。她获取消息的哈希值，然后将哈希值映射到椭圆曲线上的一个点。如果我们使用 SHA-256，我们可以将消息转换为 256 位的 x 点。如果我们无法获得曲线上的点，我们会添加一个增量值，以找到第一次到达该点的时间。消息 ($Msg$) 的签名然后用以下公式计算：

$S = sk \times H(Msg)$

其中 H(M) 是消息 ($M$) 的 256 位哈希值。她的私钥是 $sk$，她的公钥 ($P$) 等于 $aG$。然后对签名进行测试：

$e(G, S) = e(P, H(Msg))$

Zig 实现的例子在 [ 这里]:

const std = @import("std");
const bls = @import("bls.zig");
const testing = std.testing;

pub fn main() !void {
    var message: []u8 = undefined;

    var stdout_buffer: [4096]u8 = undefined;
    var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
    const stdout = &stdout_writer.interface;

    const args = try std.process.argsAlloc(std.heap.page_allocator);
    defer std.process.argsFree(std.heap.page_allocator, args);

    // Check if there are any arguments
    if (args.len > 1) {
        message = args[1];
    }

    const keypair = bls.generateBLS();

    const signature = try keypair.sign(message);

    const rtn1 = keypair.verify(message, signature);

    // Incorrect message
    const rtn2 = keypair.verify("Wrong message", signature);

    try stdout.print("BLS12-381:\n", .{});

    try stdout.print("\nMessage: {s}\n", .{message});

    try stdout.print("\nBob's private key: {x} Length: {d}\n", .{ keypair.private_key, keypair.private_key.len });
    try stdout.print("\nBob's public key: {x} Length: {d}\n", .{ keypair.public_key, keypair.public_key.len });

    try stdout.print("\nSignature: {x} Length: {d}\n", .{ signature, signature.len });

    if (rtn1 == true) try stdout.print("\nSignature verified\n", .{});
    if (rtn2 == false) try stdout.print("Incorrect Signature NOT verified\n", .{});

    try stdout.flush();
}

以及一个示例运行 [ 这里]:

BLS12-381:

Message: Hello

Bob's private key: 0d8185806e094def668fd608264fb407d5de1b57af106f6a3f06dae351535609 Length: 32

Bob's public key: d4e706d1065a3b33912fdcf9b94920952adeaaf7dc9bcee8866eba64e230c57dc44891f51507d08cf56fd57a08fc8062 Length: 48

Signature: e9c7faa1f38096fb9e7e9ad4e16a3d8c5778187b788c1ebe00f565bdd7fd8b638c968587fbd439d1f23f35924754104d5c707297420417bc611b062ff883f32bb8a7bffd36a55254a83bc7e5f558c858e72cb51d7df6a5495dcf6941fd3ba945 Length: 96

Signature verified
Incorrect Signature NOT verified

签名聚合

使用基于配对签名的最强大的技术之一，我们可以将签名聚合在一起，而仅使用公钥的聚合来验证。

总的来说，Bob 和 Alice 可以使用他们的私钥签署消息。然后我们可以聚合生成的签名（_sigmaagg），并聚合他们的公钥（_pkagg）。聚合后，我们可以使用聚合公钥验证聚合签名：

然后，我们能够使用配对操作的双线性进行聚合。对于聚合签名 ($\sigma_agg$)，我们有一个对应的聚合公钥 ($pk_agg$)​，和一个公共消息 ($m$)：

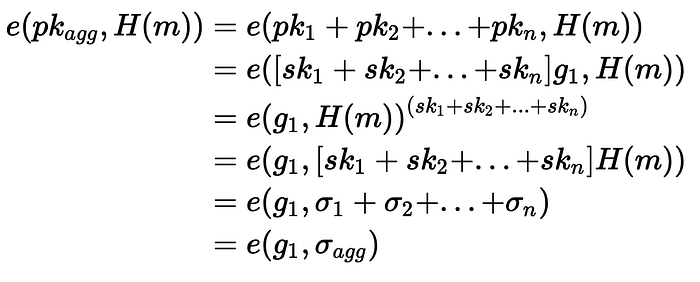
因此，我们只需要证明：

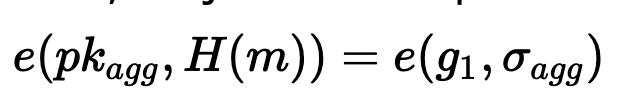
我们必须将 $H(m)$ 映射到 $G2$ 群上的一个点。以下代码使用 Zig Version 0.15.1 编译 [ 这里]:

const std = @import("std");
const bls = @import("bls.zig");

pub fn main() !void {
    var message1: []u8 = undefined;
    var message2: []u8 = undefined;
    var message3: []u8 = undefined;

    var stdout_buffer: [4096]u8 = undefined;
    var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
    const stdout = &stdout_writer.interface;
    const args = try std.process.argsAlloc(std.heap.page_allocator);
    defer std.process.argsFree(std.heap.page_allocator, args);

    // Check if there are any arguments
    if (args.len > 1) {
        message1 = args[1];
    }
    if (args.len > 2) {
        message2 = args[2];
    }
    if (args.len > 3) {
        message3 = args[3];
    }

    // Generate multiple keypairs and signatures
    const keypair1 = bls.generateBLS();
    const keypair2 = bls.generateBLS();
    const keypair3 = bls.generateBLS();

    const signature1 = try keypair1.sign(message1);
    const signature2 = try keypair2.sign(message2);
    const signature3 = try keypair3.sign(message3);

    // Signature aggregation
    const signatures = [_][bls.BLS_SIGNATURE_SIZE]u8{ signature1, signature2, signature3 };
    const aggregate_sig = try bls.aggregateSignatures(std.heap.page_allocator, &signatures);

// Aggregated signature verification
    const messages = [_][]const u8{ message1, message2, message3 };
    const public_keys = [_][bls.BLS_PUBLIC_KEY_SIZE]u8{ keypair1.public_key, keypair2.public_key, keypair3.public_key };
    const rtn = bls.verifyAggregateSignature(&messages, aggregate_sig, &public_keys);

    try stdout.print("BLS12-381 Signature Aggregation:\n", .{});
    try stdout.print("\nMessage 1: {s}\n", .{message1});
    try stdout.print("Message 2: {s}\n", .{message2});
    try stdout.print("Message 3: {s}\n", .{message3});
    try stdout.print("\nPrivate key 1: {x} \n", .{keypair1.private_key});
    try stdout.print("Public key 1: {x}\n", .{keypair1.public_key});
    try stdout.print("Private key 2: {x}\n", .{keypair2.private_key});
    try stdout.print("Public key 2: {x}\n", .{keypair2.public_key});
    try stdout.print("Private key 3: {x}\n", .{keypair3.private_key});
    try stdout.print("Public key 3 : {x}\n", .{keypair3.public_key});
    try stdout.print("\nSig 1: {x}\n", .{signature1});
    try stdout.print("Sig 2: {x}\n", .{signature2});
    try stdout.print("Sig 3: {x}\n", .{signature3});
    try stdout.print("\nAggregated Signature: {x} Length: {d}\n", .{ aggregate_sig, aggregate_sig.len });
    if (rtn == true) try stdout.print("\nSignature verified", .{});
    try stdout.flush();
}

一个示例运行是 [ 这里]:

BLS12-381 Signature Aggregation:

Message 1: Hello
Message 2: Hello2
Message 3: Hello3

Private key 1: 28f15beac21ca4d281588e60c12c69968071a59502d26ece2a49abc66c2ff71b
Public key 1: 85fab229b70db6b3578ef4fa8b8f07f911de8beb34ac3bca6c93dd9c4f8989cd394b3ddd815d6b6729cafeebe737c3b2
Private key 2: 0ce075966bf45f92c18a97db723735865ca0dbda8cfe9ff4126da45a61956829
Public key 2: a6be620f5b4548597a9a67b63d8e84a035db8a13a1a471c2ff0d0b651e073701cde32a1b98d527a18ea33c4324b9ba3a
Private key 3: 574785f7537575eaf8205ec5042dc268d9e63168f5e351a187ace454f0d90817
Public key 3 : b3c8dfb1aae133d2cb0a545cbecd59a3d245f820d66a0bee5fad6da5cb460c3f4b2e6c5f15d2f3b2764018840e7cdd01

Sig 1: fa7937963732a4497ace730c708c62f58469aa690a8c1ca64acd298499fe974d454c824f04040a60af523efebc2dd6445a1a3e9ec6256d5372c6d4909b819292ea5d21228d36ba475dffd30a4e2df4752c910f85b76cceb8e0ef2f82f5f9b10c
Sig 2: a4292d8c5225e2a58e3a30b124825fd98c115f8eae68f1a350027ab1cae07fba7c10ede4ec290c69be92935bf9a670c9cfbf7530ce5d4718729093e9c4969111bb145bd910b55a603ce9d756b8c4f483f172cb512af4dc2ddc453cd2354cbea8
Sig 3: edfeba96e826b8facc501fe4eff5b4e9146a7223c324b87c58cb3a48baa73acede7914575db3927c33d6491dccd89988a05bc35aa004c6c1577816c5af6c20476ce6787c89ce609502e5a252ddac3d22da05182e8606b5b14913ecb81aa4b326

Aggregated Signature: b3c9cc5f734297effd9cb6d70dc2480c90a4c0c58da820f47a3e5a936417d8b7fe59de4293348a507ecf735735400d0eff3a540f5347ecf0481f1a17917e7cabd127c17b6f87d3eb4dfd209742cf5103eda34dcdb2ce377bd19572c154ae191d Length: 96

Signature verified

有了这个，私钥是 32 字节长，公钥是 48 字节长，签名总是 96 字节长。

门限签名

使用 BLS 签名最强大的要素之一是，我们可以将私钥拆分为多个份额，然后使用这些份额来创建签名门限。在下面，我们将密钥拆分为 Bob、Alice 和 Carol 的三个部分，并定义任何两个份额可以合并在一起以签署消息：

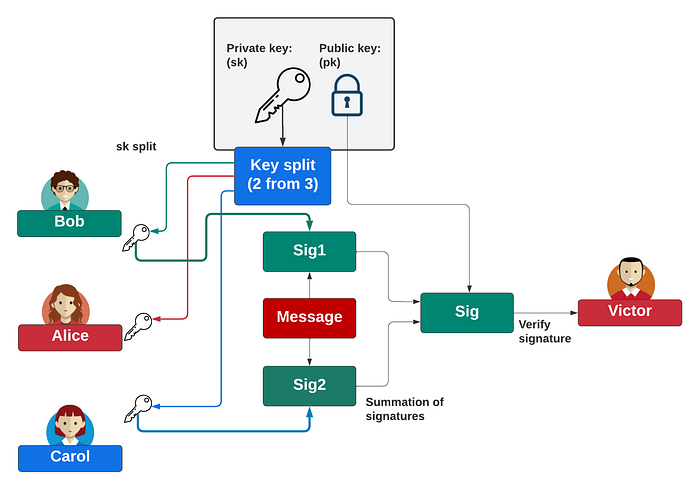
在此代码中，我们可以从五个签名中选择任意三个来创建一个有效的签名 [ 这里]:

const std = @import("std");
const bls = @import("bls.zig");

pub fn main() !void {
    var message: []u8 = undefined;

    var stdout_buffer: [4096]u8 = undefined;
    var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
    const stdout = &stdout_writer.interface;

    const args = try std.process.argsAlloc(std.heap.page_allocator);
    defer std.process.argsFree(std.heap.page_allocator, args);

    // Check if there are any arguments
    if (args.len > 1) {
        message = args[1];
    }

    const main_key = bls.generateBLS();
    const private_key = main_key.private_key;

    const threshold: u32 = 3;
    const m_shares: u32 = 5;

    // Generate shares
    const shares = try bls.ThresholdBLS.generateShares(std.heap.page_allocator, threshold, m_shares, private_key);

    const signature1 = try bls.signBLS(message, shares[0].private_share);
    const signature2 = try bls.signBLS(message, shares[1].private_share);
    const signature3 = try bls.signBLS(message, shares[2].private_share);

    const signatures = [_][bls.BLS_SIGNATURE_SIZE]u8{ signature1, signature2, signature3 };
    const aggregate_sig = try bls.aggregateSignatures(std.heap.page_allocator, &signatures);

    const rtn = main_key.verify(message, aggregate_sig);

    try stdout.print("BLS12-381 Threshold Signatures (3 from 5):\n", .{});

    try stdout.print("\nMaster Key private: {x} \n", .{private_key});
    try stdout.print("Master Key public {x}\n", .{main_key.public_key});

    for (shares, 0..) |share, i| {
        try stdout.print("\n{d} Index: {d} Public share: {x}, Private share: {x}\n", .{ i, share.index, share.public_share, share.private_share });
    }
    try stdout.print("\nRecovered signature: {x} \n", .{aggregate_sig});

    if (rtn == true) try stdout.print("\nSignature verified\n", .{});

    try stdout.flush();
}

一个拆分私钥的示例运行是：

BLS12-381 Threshold Signatures (3 from 5). Message: hello

Master Key private: a5fb156db72749b884ad40eb76367f4bef87ae907511157c11feffd9ba2ebc0c
Master Key public d2a9826400858e4a0170a166902a3e738fc370f918fad05ceee83c1fcc678703c5e3b2a9dffd972227cd0f229482f65d

0 Index: 1 Public share: dc69880288dd03f407e0819ccfeec0dd439e00f689ac020f53f0c455476ac0470451e35ff6f744cf53a65bdfe0fe7a4b, Private share: 481e69302b47133646c43a541f908edbd602e5850fe56ff62c2e4618060e0422

1 Index: 2 Public share: c657a1a243749af5dbf0471d302ce2c960e1ea507a3e4462d71f431d2e0c0a8d96d004a85aa2a7e5384733c3a89d657d, Private share: eb31036d4b6006fb2faabcb45838c64bbb7e669d9c2a98983cac8bee724be302

2 Index: 3 Public share: ea0b54790ee1434712fdfb1c649563ced49e6396f63b3b17ef8016a600b3b73f6abbe21115c9503fc2458391aa9e9304, Private share: 7fce03276453f23d05209b2b9e42b740c8a540ef77c8af7072f79676cca9b238

3 Index: 4 Public share: dcc2ccbd223933526a6835c4d36bf772b451c81612e7050c29a0ae3b7bff3c72f041cd7bfdde1a09814603940977fd88, Private share: 9ed5c9bff34a0762ae5c61902cbb031bbee9a847413ed42a693b9a9cd7e60816

4 Index: 5 Public share: 876cc7ca3301d2a9fdb8023d8d640f20b2f38da2ba796b0bc3a6fd4d868e2a4eba94976b53f8d4488479e25b5c3552c6, Private share: 2d3ea0b923c89dfbcbf87c243b1e02760638ba4b9d34fb9e357fa780cc786f15

Recovered signature: a82189effc6680d2e66c3d2b9b4b79e836e8321e6e994389e7a8173fe83d3c47e758d300d52e73476bd0acccec0151b8d9893ebd90875634fc1f884765bfee2d5e3598a3107e5dc777a0bdbba47745502602b44811847d5e5d141ba65e176570

Signature verified

为什么？

这种方法在数字信任应用程序中很有用，多个签名者可以一起使用，并使用他们自己的私钥签署他们签名的一部分，然后聚合器可以将签名汇集在一起，并聚合签名者的公钥以获得一个公钥，该公钥可以检查所有签名者是否已批准该交易。

这里是 Zig 中的示例：

BL12-381 和 Zig

聚合的 BL12-381 签名和 Zig

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～