证明聚合技术

介绍

SNARKs（简洁的、非交互的知识论证）和 STARKs（可扩展的、透明的知识论证）由于它们在去中心化私有计算和扩展区块链中的应用而受到了广泛关注。它们是让我们向另一方证明我们正确完成了一项计算的工具，这样验证速度比重新执行计算快得多。证明的大小比证明它所需的所有信息小得多。 例如，我们可以证明我们知道数独游戏的解决方案，而无需完全提供它。在虚拟机执行的情况下，为了证明正确性，我们应该看到机器的寄存器在每个周期如何变化；验证者不需要完全知道它，而是查询某些点的寄存器。有关 SNARKs/STARKs 的影响的讨论，请参阅我们的文章。

证明大型程序或计算可能很昂贵，因为这会给运行它们带来开销。在某些情况下，计算可以分解为几个较小的计算（例如，证明一个区块内的交易可以通过分别证明每笔交易来完成），但这有两个缺点：证明大小和验证时间随着组件的数量线性增加。两者都会损害可扩展性，因为我们需要更多时间来验证整个计算，并且会增加内存使用量。我们可以通过捆绑所有证明并仅进行一次验证来解决这个问题。我们可以使用多种技术；最好的技术将取决于我们使用的证明系统的类型和我们的特定需求。本文将讨论我们拥有的一些替代方案，以及它们在证明者时间、验证时间和证明大小方面的权衡。

聚合技术

这些技术将允许我们一起证明几个陈述，从而减少了检查几个陈述所带来的证明大小和验证时间的膨胀。有关某些技术的解释，请参阅以下视频。

证明递归

SNARKs/STARKs 让我们以时间和内存高效的方式检查任何 NP 语句的有效性。证明一个语句所需的信息量远小于检查该语句所需的 witness 的大小。例如，在 STARKs 中，验证者不需要查看程序的整个执行轨迹；它只需要一些随机查询。在 Plonk 中，验证者具有轨迹多项式在随机点的评估值，这远小于轨迹中的 $3n$ 个值。

递归是如何工作的？证明者证明他验证了一个证明 $\pi$，该证明对应于具有公共输入 $u$ 的某个计算。下图显示了递归的流程。

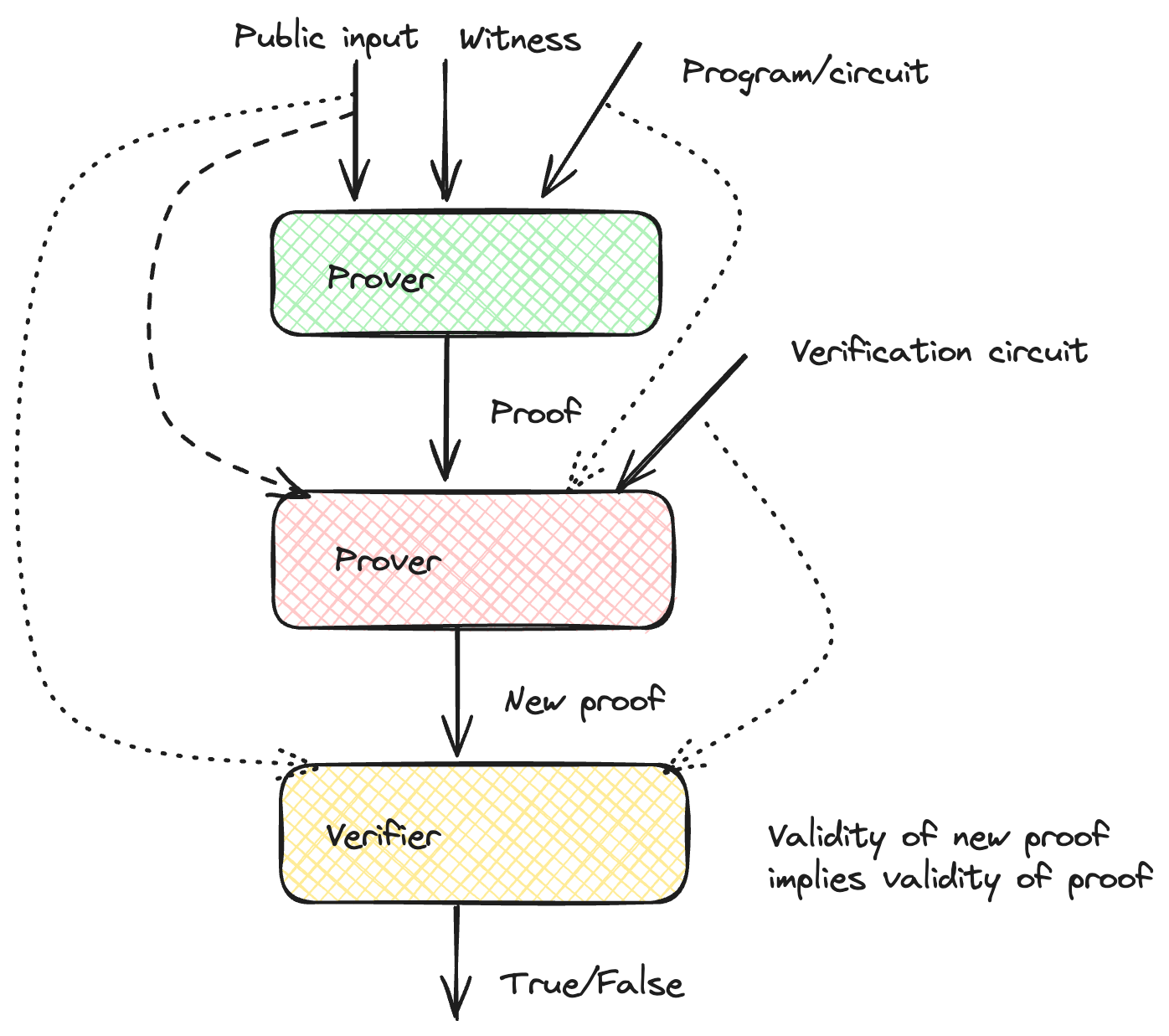
证明者获取公共输入、witness 和程序，并生成证明 $\pi$，证明计算的有效性。 然后，证明者将证明 $\pi$ 和原始电路作为 witness，将公共输入和验证电路（验证者必须执行以检查语句的操作）作为输入，并获得一个新的证明 $\pi'$，表明证明者知道证明 $\pi$，该证明 $\pi$ 使用给定的输入满足验证电路。 验证者可以检查证明 $\pi'$，表明证明者所做的验证是有效的，这反过来意味着第一次计算的正确性。 在 STARKs 的情况下，如果验证操作的轨迹比原始程序的轨迹短，则证明大小和验证时间会减少（因为它们取决于轨迹长度 $n$）。

我们也可以使用两个不同的 prover。 例如，我们可以使用 STARKs 证明第一个程序，该程序速度很快但证明较大，然后使用 Groth 16/Plonk，该程序具有较小的证明大小。 优点是第二种情况不需要处理任意计算，因此我们只能有一个优化的电路用于 STARK 验证。 结果是一个小的证明，具有快速验证。

我们还可以使用相同的结构并证明多个证明的验证。

我们面临的一个问题是，即使证明大小减小了，公共输入也会线性增加。 我们可以通过提供所有公共输入的 hash/承诺并将它作为 witness 的一部分来解决这个问题。 在验证期间，我们必须检查 witness 中公共输入的 hash 是否对应于公共输入的 hash/承诺。 通过构建树结构可以更有效地处理证明递归，从而提高并行化程度。

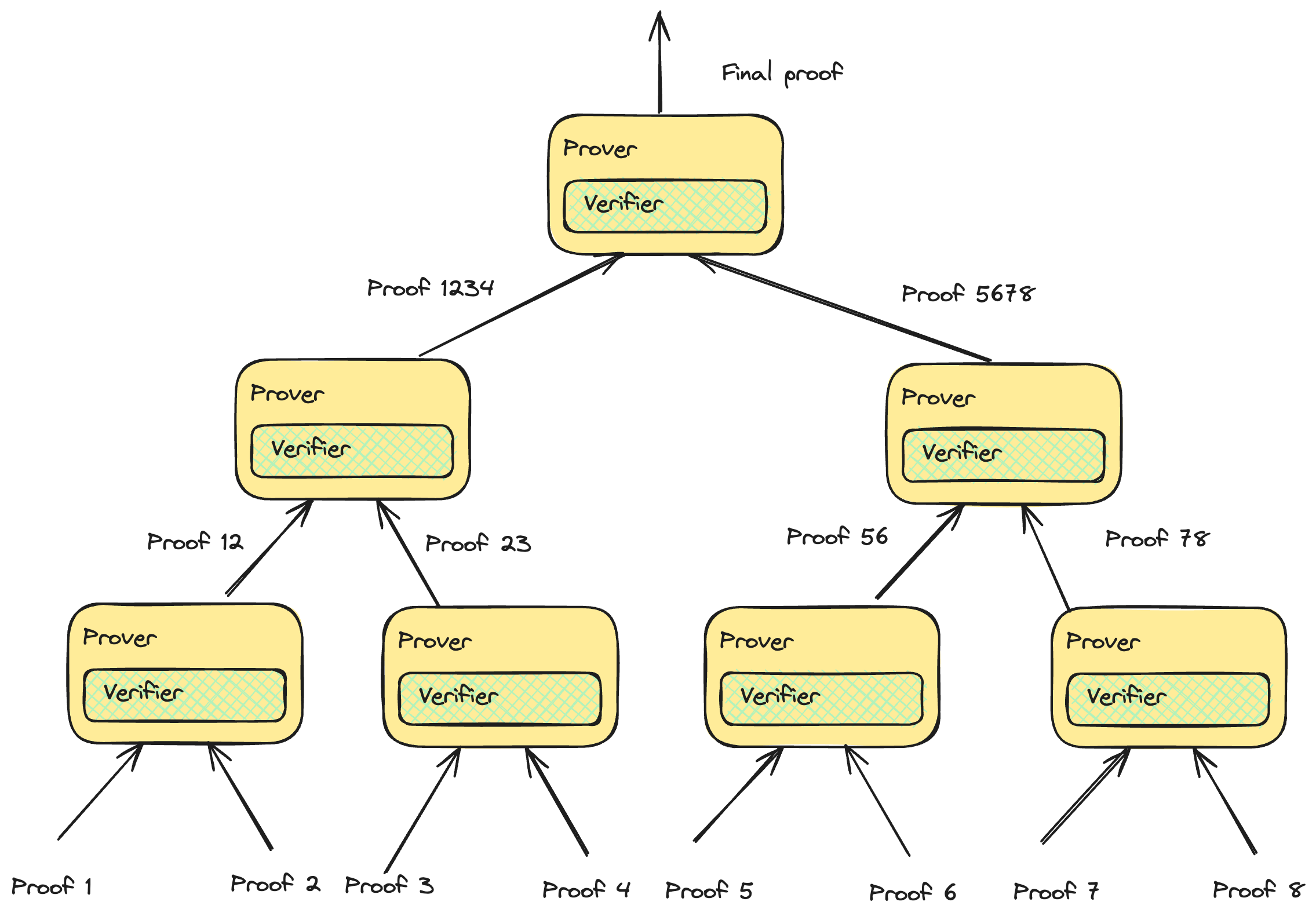
证明递归在多个项目中用于减少证明大小并使验证更便宜，例如 Starknet、Polygon ZKEVM 和 zkSync。

即使证明递归有很多优点，它也会增加证明者的工作量。 在 STARKs 等证明系统中，证明者必须计算大量 hash，这些都是昂贵的操作。 幸运的是，在代数 hash 函数（证明成本较低）和 STIR 等协议方面已经取得了进展，这些协议减少了生成证明所需的 hash 数量(文章即将推出)。 在椭圆曲线上工作的 SNARKs 中，证明由曲线中的元素（坐标位于字段 $F_p$ 上）和以 $F_q$（标量字段）表示的标量组成。 这产生了一个问题，因为我们必须在 $F_p$ 上执行操作才能计算曲线上的操作。 尽管如此，电路中的标量位于 $F_r$ 中，从而导致非本地字段操作。 这里 你可以找到一个电路来验证 Groth 16 证明，大约需要 2000 万个约束。 正如以下部分所讨论的，曲线循环是避免字段仿真的更好选择。

曲线循环

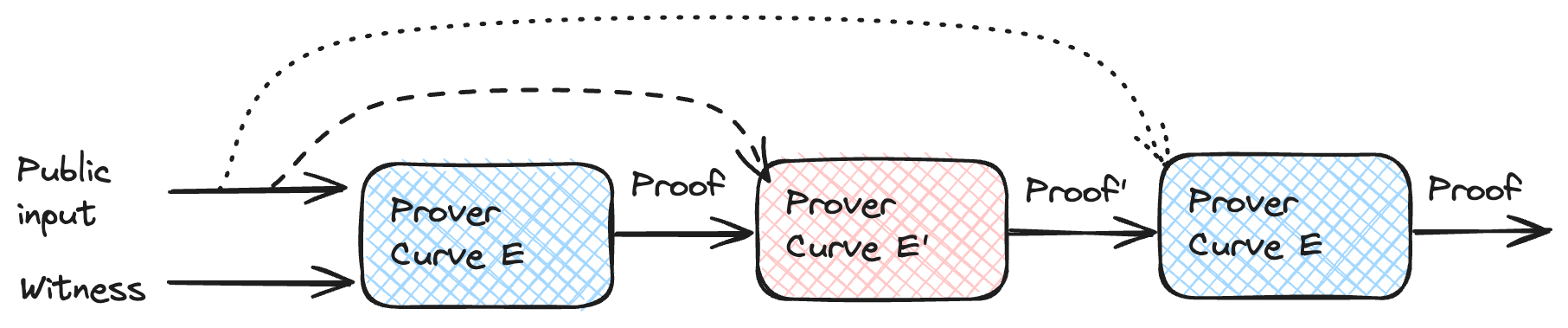
我们遇到了曲线 $E$ 的坐标位于 $F_p$ 中，但标量字段为 $F_r$ 的问题。 如果我们可以找到一条在 $F_r$ 上定义且标量字段为 $F_p$ 的曲线 $E'$，那么我们可以使用 $E'$ 检查 $E$ 上的证明。 具有这些特征的曲线对称为曲线循环。 幸运的是，一些形式为 $y^2 = x^3 + b$ 的曲线满足这些条件。 Pallas 和 Vesta 曲线（统称为 Pasta 曲线）形成一个循环，并在 Mina's Pickles 和 Halo 2 中使用。 我们在之前的 文章 中介绍了 Pickles 的一些基础知识。 Pickles 使用两个累加器（每个累加器使用不同的曲线）并将一些检查推迟到下一步。 这样，它可以避免昂贵的验证并有效地提供增量可验证计算。

折叠和累积方案

完全递归的缺点之一是我们需要证明整个验证过程，这可能非常昂贵。 例如，在递归 STARKs 中，我们必须计算所有 hash 并验证所有代数运算才能获得新的证明。 折叠方案通过组合多个实例并累积它们来提供完全验证的替代方案。 Nova 引入了 R1CS 的折叠方案。 关键思想是，如果我们有两个 R1CS 的解 $(u_1, w_1)$ 和 $(u_2, w_2)$，我们可以将它们组合成一个对提交的松弛 R1CS（R1CS 的泛化）的单个声明 $(u, w)$。

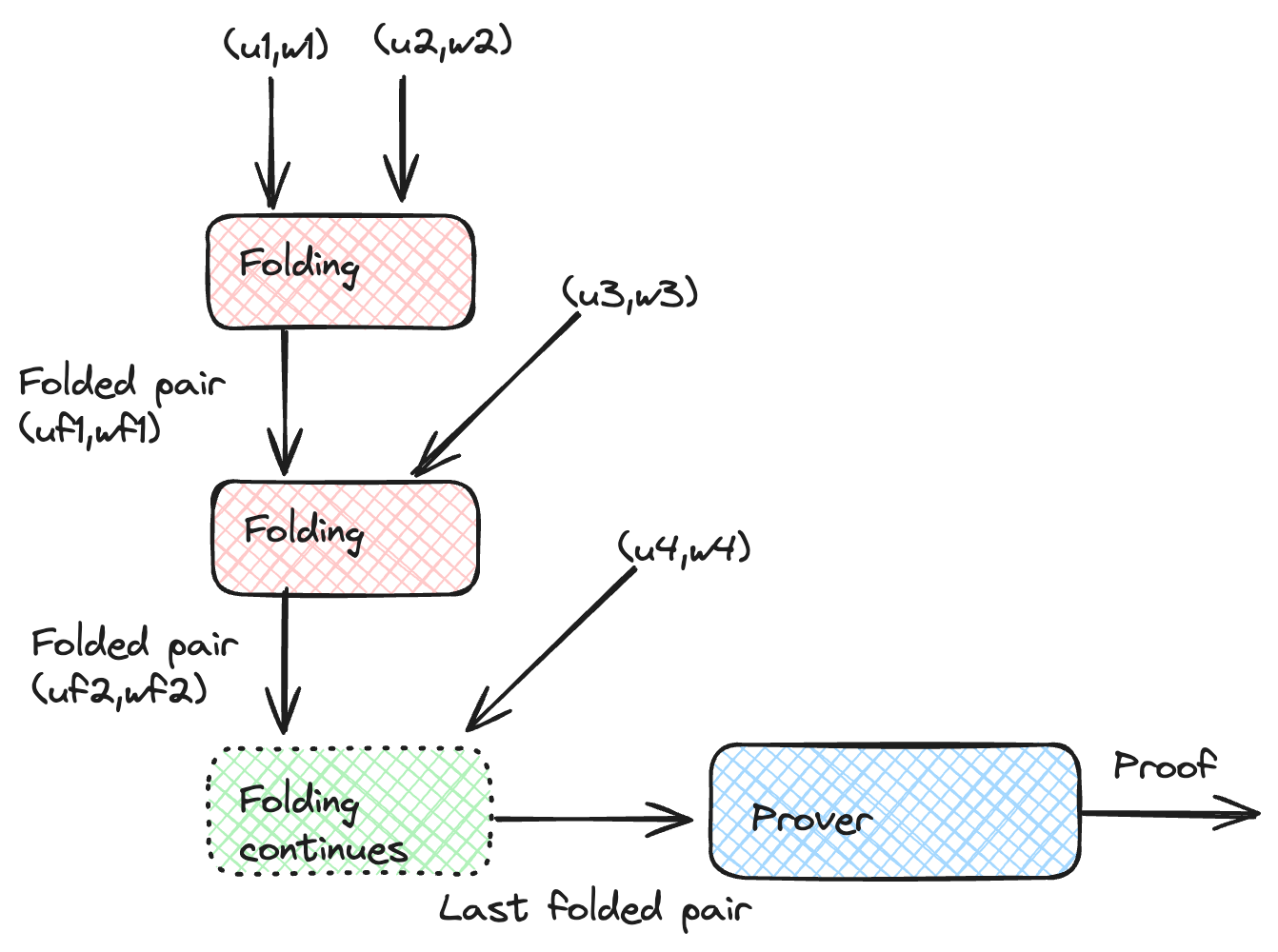
然后我们可以为统一的声明生成一个证明，这相当于所有实例的有效性。

SNARKPack

一些证明系统具有可以通过其他方法聚合的证明，例如 Groth 16 的 SNARKPack。 Groth 16 的证明由三个元素 $\Pi = (\pi_1, \pi_2, \pi_3)$ 组成，其中 $\pi_1, \pi_3$ 属于椭圆曲线的群 $G_1$，$\pi_2$ 属于 $G_2$。 Groth 16 中的检查是以下配对等式，

$e(\pi_1, \pi_2) = Y e(\pi_3, D)$

其中 $Y$ 取决于公共输入和仪式的参数，$D$ 是参数的一部分。 如果我们有几个证明 $\Pik = (\pi{1k}, \pi{2k}, \pi{3k})$，我们可以结合不同的检查，

$e(\pi{1k}, \pi{2k}) = Yk e(\pi{3k}, D)$

使用随机数 $r_k$，使得

$\prod e(\pi{1k}, \pi{2k})^{r_k} = \prod Y_k^{rk} \prod e(\pi{3k}, D)^{r_k}$

我们可以将其改写为

$Z_{AB} = Y' e(Z_C, D)$

其中

$Z{AB} = \prod e(\pi{1k}, \pi_{2k})^{r_k}$

$Y' = \prod Y_k^{r_k}$

$ZC = \prod \pi{3k}^{r_k}$

验证者需要检查 $Z_{AB}$ 和 $Z_C$ 是否与提供的证明三元组 $\Pi_k$ 一致。 这是通过目标内部配对乘积和多指数内部乘积来完成的。 优点是组合证明大小实际上与聚合的证明数量无关。

延续

延续是一种机制，通过该机制，我们可以将复杂的计算分成可以单独计算和证明的较小部分。 这可以通过利用并行化和减少 prover 的内存占用来实现更快的证明。 缺点是，除非以 rollup 形式实现，否则证明大小会膨胀。 但是，让我们利用独立证明并使用折叠方案将所有声明组合到同一验证电路或递归证明。 我们可以将所有段包装成一个证明（这也可能是一个具有恒定证明大小的 SNARK）。

总结

在过去的十年中，我们看到了新型证明系统和技术的发展，以时间和内存高效的方式显示计算的有效性。 但是，我们需要将大型计算分解为较小的独立计算（例如，通过分别证明每笔交易来证明一个区块的交易）。 缺点是我们的证明大小和验证时间都会膨胀，这会损害可扩展性或增加成本。 幸运的是，有几种聚合证明的技术，因此验证单个证明意味着验证所有其他证明。 虽然证明递归提供了一种高度并行化的证明聚合方式，但它涉及昂贵的操作，例如字段仿真和 hash 函数。 累积或折叠方案通过将一些检查推迟到最终验证步骤来提供完全验证的替代方案。

• 原文链接： blog.lambdaclass.com/pro...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～