二次剩余与三次剩余

二次和三次剩余

在密码学中，我们寻找难以解决的问题。为此，我们可以创建后门来解决它。对于离散对数，我们使用以下难题：

$Y=g^x \pmod p$

即使我们知道 $g$、$Y$ 和 $p$，也很难确定 $x$，只要素数足够大。RSA 公钥方法中使用了另一个难题，它涉及模数 ($N$) 分解的难度，模数由两个素数组成。

另一个难题是模 $n$ 的二次剩余，它使用以下形式：

$x^2 \equiv a \pmod p$

我们必须找到一个 $x$ 值，该值产生 $a \pmod p$ 的值。如果存在解，则值 $a$ 是 二次剩余 (mod n)。同样，我们可以有三次剩余：

$x^3 \equiv a \pmod p$

我们需要找到是否存在可能的解决方案。

二次剩余

在模运算中，此运算等效于一个数的平方根（其中 $x$ 是 $a$ 模 $p$ 的模平方根）。在下文中，我们将尝试找到 $x$ 的值，并生成勒让德符号值。

例如，如果 $a = 968$ 且 $p = 1223$，则得到：

求解 $x^2 \equiv 968 \pmod {1223}$ [答案: 453] 尝试!

另一个例子：

求解 $x^2 \equiv 1203 \pmod {1223}$ [答案: 375] 尝试!

因此，968 和 1203 是模 1223 的二次剩余。

$x^2 \equiv a \pmod p$ 的形式并非总是可解的。例如，如果 $a = 209$ 且 $p = 1223$，则得到：

$x^2 \equiv 209 \pmod {1223}$

没有解决方案。此外，如果 $a$ 与 $p$ 共享一个因子，则也是不可解的。例如：

$x^2 \equiv 39 \pmod {13}$

将为 $x$ 返回零值。

如果我们取 $p = 53$ 的值，我们将得到以下值 [这里]：

0, 1, 4, 6, 7, 9, 10, 11, 13, 15, 16, 17, 24, 25, 28, 29, 36, 37, 38, 40, 42, 43, 44, 46, 47, 49, 52

代码的示例运行如下：

Quadradic residue (mod n) solver
 a: 47
 p: 53We need to solve for:
  val^2 =  47 (mod  53 )
-----------------------
Result: 10
( 10 )^2 =  47 (mod  53 )-----------------------
For a prime number of  53 here are the residues up to p (or 100)
1 4 6 7 9 10 11 13 15 16 17 24 25 28 29 36 37 38 40 42 43 44 46 47 49 52

在这种情况下，我们看到 10 是 $p$ 为 53 的可能的二次剩余。因此，解决方案是：

$10^2 \equiv 47 \pmod {53}$

你可以在这里 看到演示，以下是一些示例：

• 求解 $x^2 \equiv 12 \pmod {13}$ [答案: 8] 尝试!
• 求解 $x^2 \equiv 968 \pmod {1223}$ [答案: 453] 尝试!
• 求解 $x^2 \equiv 1203 \pmod {1223}$ [答案: 375] 尝试!
• 求解 $x^2 \equiv 47 \pmod {53}$ [答案: 10] 尝试!
• 求解 $x^2 \equiv 209 \pmod {1223}$ [无解!] 尝试!
• 求解 $x^2 \equiv 888 \pmod {1223}$ [无解!] 尝试!
• 求解 $x^2 \equiv 39 \pmod {13}$ [无解!] 尝试!

三次剩余

如果我们有 $x^3 \equiv a \pmod p$ 的形式，我们必须找到一个 $x$ 值，该值产生 $a \pmod p$ 的值。实际上，这是一个难以解决的问题。如果存在解，则值 $a$ 是 立方剩余 (mod p)。在模运算中，此运算等效于一个数的平方根（其中 $x$ 是 $a$ 模 $p$ 的模立方根）。在这种情况下，我们将确定是否存在立方根，然后，如果可能，找到一个解。对于解，我们测试 $a^{ ( p −1)/ gcd(3, p −1)} \equiv 1 \pmod p$。

对于三次剩余，我们有 $x$ 的解：

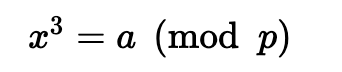
为此，如果满足以下条件，我们有一个解决方案：

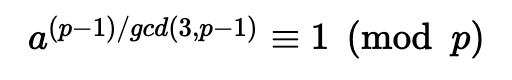
对于 $x^k = a \pmod p$

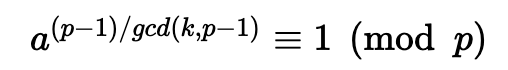
如果素数 ($p$) 是：

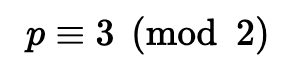
那么解决方案是：

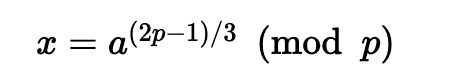
例如，是否有以下解决方案：

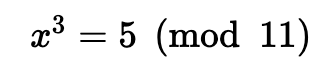
为此，我们得到：

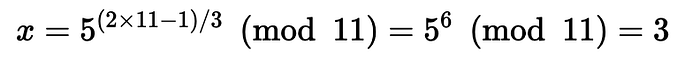
我们看到我们有一个解决方案：

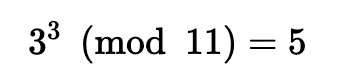
以下是一些示例：

• $a = 3, p = 11$ 尝试。$x^3 \equiv 3 \pmod {11}$。
• $a = 5, p = 11$ 尝试。$x^3 \equiv 5 \pmod {11}$。
• $a = 15, p = 59$ 尝试。$x^3 \equiv 15 \pmod {59}$。
• $a = 23, p = 59$ 尝试。$x^3 \equiv 23 \pmod {59}$。
• $a = 31, p = 59, q = 67$ 尝试。$x^3 \equiv 31 \pmod {59}$。

代码如下：

import sys
import random
import libnum
import math

p=11
a=25
if (len(sys.argv)>1):
        a=int(sys.argv[1])
if (len(sys.argv)>2):
        p=int(sys.argv[2])

print ("p=",p)
print ("a=",a)
print ("\n\nFind solution to x^3 = a (mod p)")
## 查找 x^3 = a (mod p) 的解
if (pow(a,(p-1)//math.gcd(3,p-1),p)):
 print(f"对于 x^3={a} (mod {p})，存在立方根的解")
 if (p%3==2):
  sol = pow(a,(2*p-1)//3,p)
  print(f"   The solution is {sol}^3 (mod {p}) = {a}")
else:
 print(f"对于 x^3={a} (mod {p})，不存在立方根的解")

一个示例运行是：

p= 11
a= 25
Find solution to x^3 = a (mod p)
对于 x^3=25 (mod 11)，存在立方根的解
   The solution is 9^3 (mod 11) = 25

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～