现代密码学
- 不会喷火的小火龙
- 发布于 2025-12-08 14:35
- 阅读 1305
绪论信息安全三大核心要素(CIA三元组)是指:保密性、完整性、可用性系统保密性不依赖于加密体制或算法的保密,而依赖于密钥。被动攻击:获取信息内容;进行业务流分析(流量分析)主动攻击:伪装、重放、信息修改、拒绝服务信息系统的安全性:保密性、数据完整性、实体认证、消息认证、可用性、访问控制、可
绪论
信息安全三大核心要素(CIA三元组)是指:保密性、完整性、可用性
系统保密性不依赖于加密体制或算法的保密,而依赖于密钥。
被动攻击:获取信息内容;进行业务流分析(流量分析)
主动攻击:伪装、重放、信息修改、拒绝服务
信息系统的安全性:保密性、数据完整性、实体认证、消息认证、可用性、访问控制、可控性、不可否认性
攻击类型:
- 唯密文攻击(最难)
- 已知明文攻击:已知一个或多个密文对
- 选择明文攻击:自己选择明文信息
- 选择密文攻击:自己选择密文信息
传统加密技术(古典密码)
一些概念:明文、密文、加密、解密、加解密算法、密钥

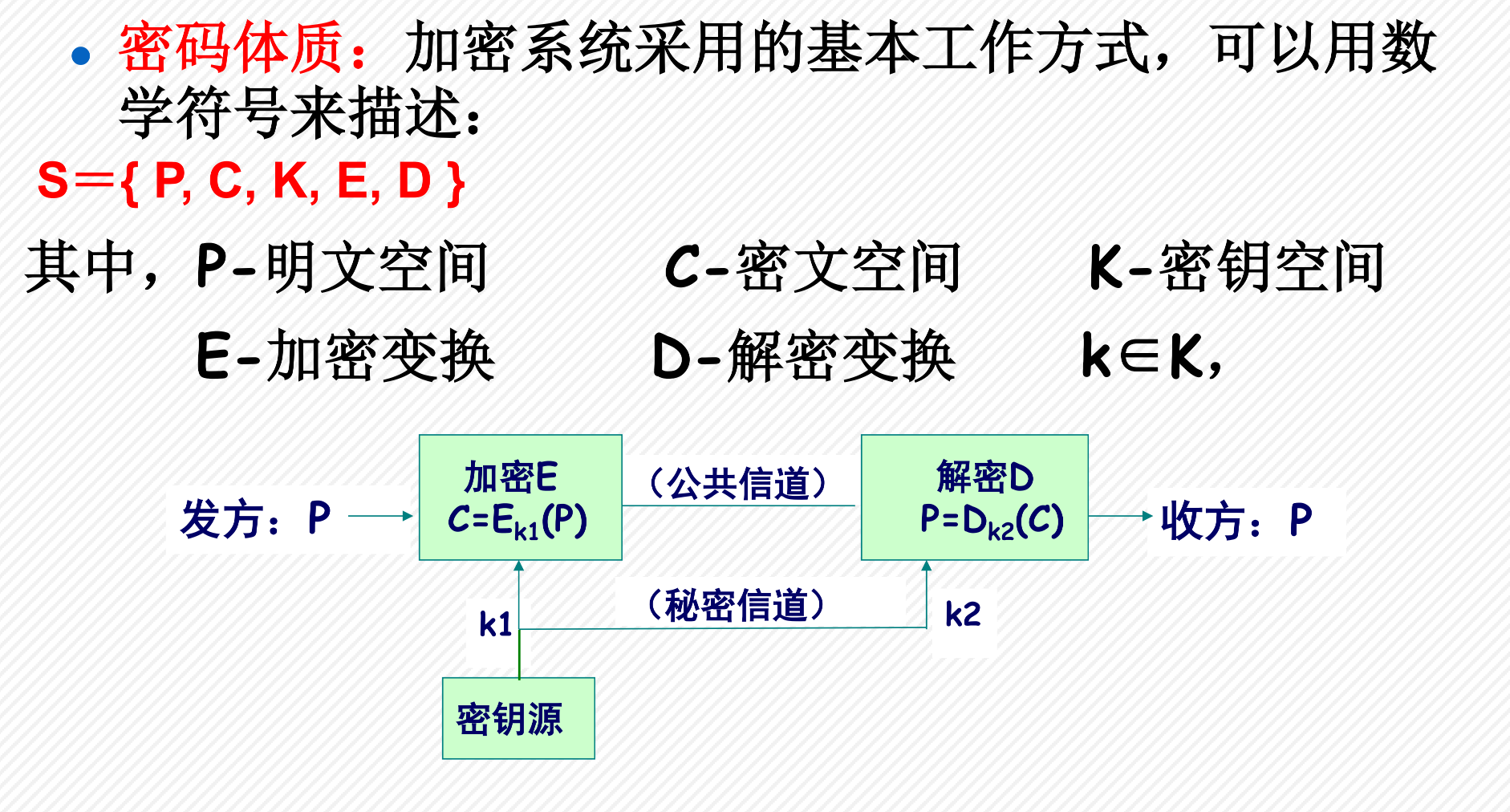
加密算法的两个原理:代换和置换
单表代换
凯撒密码


playfair密码
- 构建矩阵:密钥去重后填入,按字母表顺序填入剩余字母,I和J视为同一字母
- 整理明文:如果在同一组中出现两个相同的字母必须在中间插入填充字母(通常是
X)。 - 加密变换
- 同行:每个字母向右移一格(最右边跳回最左边)。
- 同列:每个字母向下移一格(最下边跳回最上边)。
- 矩形(不同行不同列):取其对角线上的字母(注意:保持原来字母所在的行)。


多表代换
维吉尼亚密码


一次一密
密钥只对一个信息进行加密,之后就丢弃不用。属于流密码
每一条新信息都需要一个与其等长的新密钥。
一次一密 (OTP) 虽然是无条件安全的,但它要求密钥长度必须大于等于明文长度。
置换技术
- 数密钥长度:密钥有几个数,就画几列的表格。
- 标号:把密钥数字写在表格最上方。
- 填空:把明文老老实实横着填进去,如果最后一行没填满,通常要补位(比如补 X 或 Y)。
- 找顺序:
- 眼睛在密钥里找数字
1,把那一列抄下来。 - 找数字
2,把那一列抄下来。 - 直到抄完所有列。
- 眼睛在密钥里找数字

 Hill密码:本质上是矩阵运算结合同余方程组
Hill密码:本质上是矩阵运算结合同余方程组
$$ C = P \times K \pmod{26} $$
$$ K = P^{-1} \times C \pmod{26} $$
- $C$:密文向量 (Ciphertext)
- $P$:明文向量 (Plaintext)
- $K$:密钥矩阵 (Key Matrix)
- mod 26:所有运算结果都要对 26 取余数,保证结果还在 0-25 (A-Z) 之间。
参考例题:


- 数字化
- 建立方程组求解$2 \times 2$的矩阵$K$
- 第三步:解矩阵方程 (求解 K)
选取的明文矩阵必须是可逆的。也就是说,这个矩阵的行列式(Determinant)不能是 0,而且行列式的值必须与 26 互质(Coprime),
轮转机的密钥空间是:26^3
流密码
密钥发生器f 通过密钥k 产生了密钥流
如果一个比特流是一个周期序列,则它一定是线性反馈移位寄存器序列
状态周期为2^n-1
数论
不是所有整数模n都有本原根
本原根个数为$\phi(\phi(p))$
分组密码
与流密钥都是单钥体制,但是分组密码没有记忆性
扩散和混淆是Shannon提出的设计密码系统的两个基本方法
- 扩散让明文和密文之间的关系更复杂;混淆让密文和密钥之间的关系更复杂
- P盒(置换)用于扩散;S盒(代换)用于混淆
乘积密码就是指顺序地执行两个或多个基本密码系统,使得最后结果的密码强度高于每个基本密码系统产生的结果,中间还包括置换和代换,也就是刚刚提到的扩散和混淆。
Feistel密码结构是分组密码中的一种对称结构,能自己画出来一轮

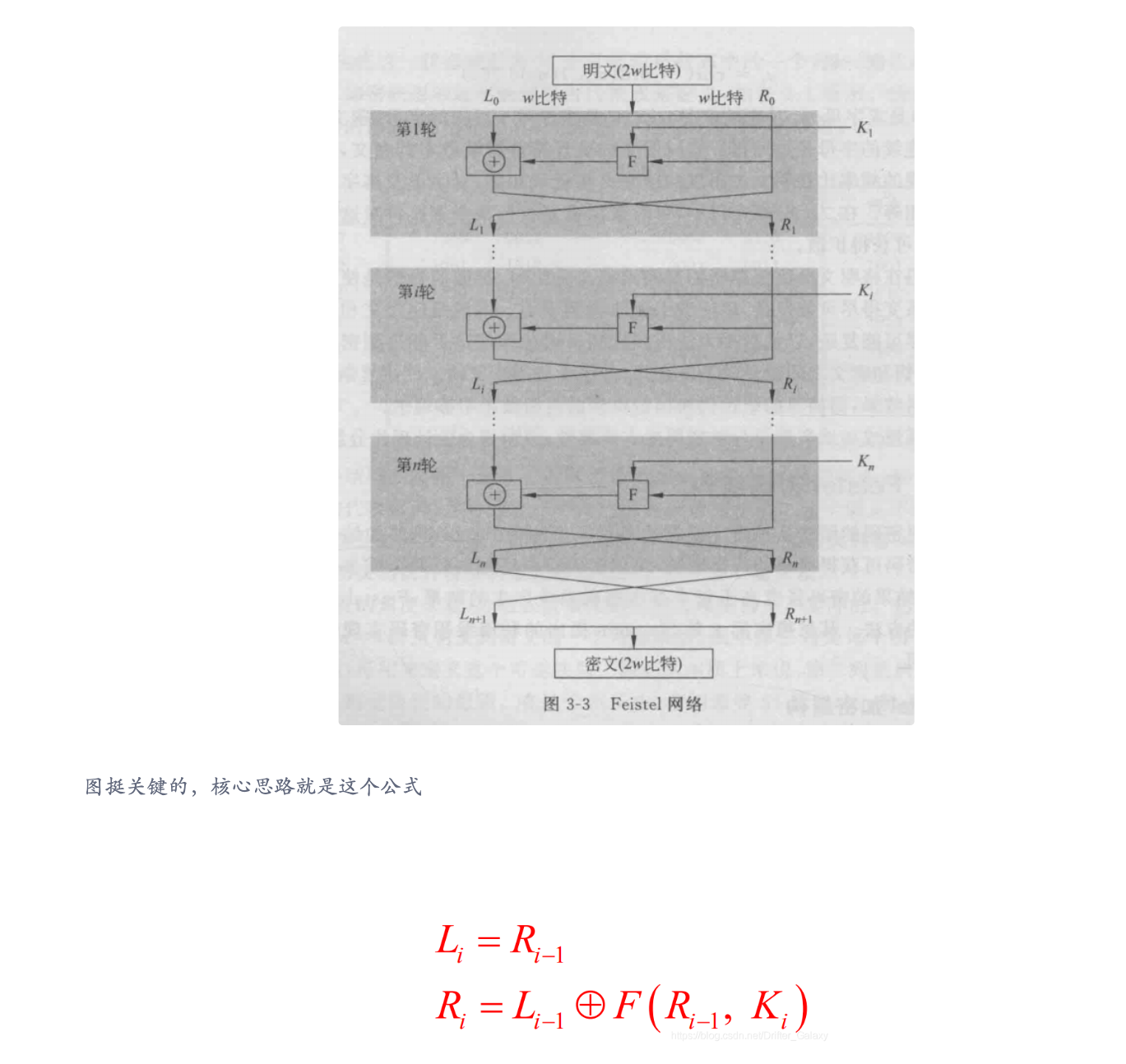
最后一轮交换左右两边的数据(置换)
这个算法就是:每组明文分成左右两边,左边就等于上一轮的右边,而右边则是用 f 对上一轮的右边通过密钥 k 进行加密,再和左边异或一下,进行n轮迭代,最后一轮要置换一下,再合在一起,就完成了。怎么和des这么像,巧了,des就是这种结构。
DES
主要流程:
- 首先进行初始置换 (IP),打乱明文顺序。
- 进入16 轮 Feistel 结构迭代。在每一轮中,数据分为左右两部分,右半部分经过轮函数(包含扩展、异或子密钥、S盒代换、P盒置换)后与左半部分异或。
- 第 16 轮结束后,进行左右 32 位交换。
- 最后进行初始逆置换 ($IP^{-1}$),输出 64 位密文。
填空:
- 分组长度:64 bit。DES 是一块一块加密的,每一块 64 位。
- 密文长度:64 bit。输入多少,输出就是多少。
- 密钥长度:56 bit。
- 专家注:你可能会在书上看到“64位密钥”,那是包含了 8 位奇偶校验位。真正参与加密运算的只有56位。
F轮函数步骤为
- 扩展 (E-box):把 32 位扩展成 48 位(为了能和 48 位子密钥进行异或)。
- 异或 (XOR):数据与子密钥混合。
- S盒代换 (S-Box) —— ⚠️最关键考点:
- 把 48 位压缩回 32 位。6bit输入中第1和第6比特组成的二进制 数确定的行,中间4位二进制数用来确定的列
- 地位:它是 DES 中唯一的非线性变换。
- 作用:如果没有 S 盒,DES 就是一堆线性的异或运算,极其容易被破解。S 盒提供了混淆 (Confusion) 特性。
- P盒置换 (P-Box):最后再打乱一次顺序(提供扩散 (Diffusion) 特性)。
Function F(R[32], K[48]):
# 1. 扩展 E: R32 -> ER48
ER = Expansion_E(R) # 按固定表,输出 48 位
# 2. 与子密钥异或
X = ER XOR K # 48 位
# 3. 分成 8 组,每组 6 位,映射到 4 位
For j = 1..8:
block6 = X[6*(j-1) .. 6*j -1] # 取第 j 组 6 位
row = (block6[0] << 1) | block6[5]
col = (block6[1]<<3) | (block6[2]<<2) | (block6[3]<<1) | block6[4]
out4 = Sbox_j[row][col] # 0..15
Sout[4*(j-1) .. 4*j -1] = bin4(out4)
# 4. P 置换
return Permutation_P(Sout) # 32 位密钥生成算法:DES 的密钥作用发生在 F 函数内,对右半部分扩展后的 48 位数据进行 XOR。16 个子密钥分别对应 16 轮。

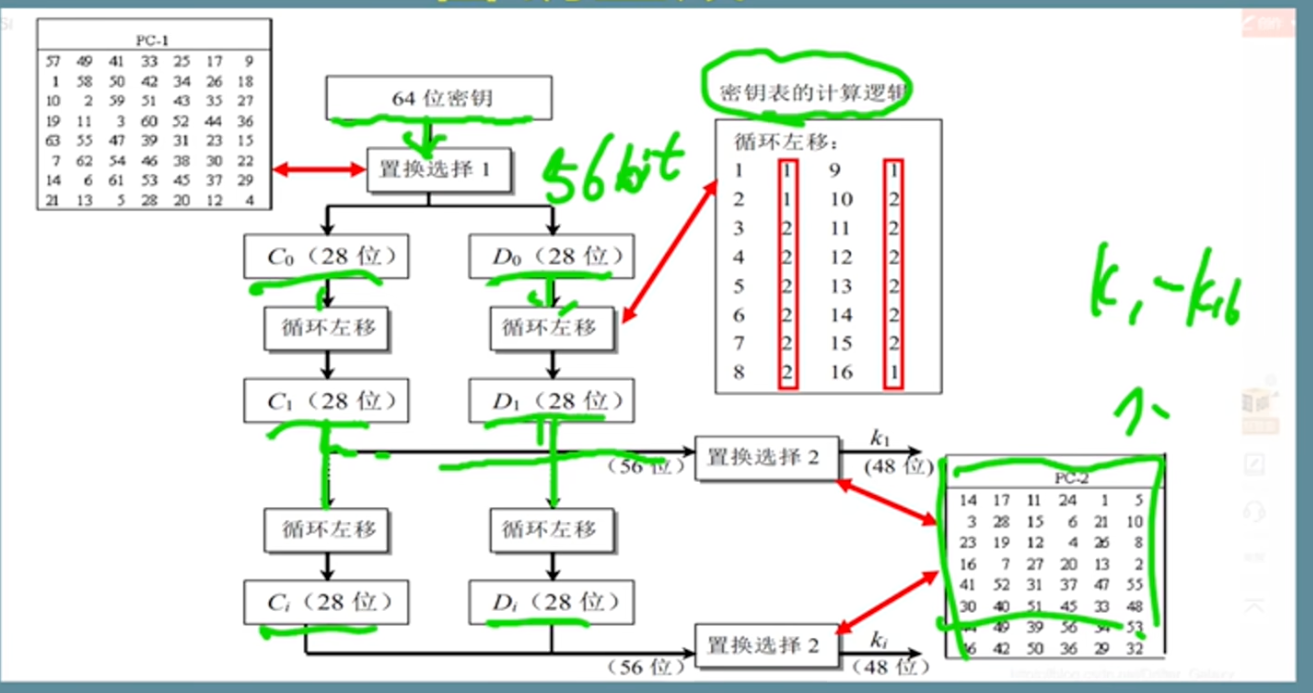 |
步骤 | 输入位数 | 输出位数 | 核心动作 | 备注 |
|---|---|---|---|---|---|
| PC-1 | 64 | 56 | 去校验位 + 置换 | 分为$C_0, D_0$ 两部分 | |
| 循环左移 | 28 + 28 | 28 + 28 | 每一轮根据规则左移 1 或 2 位 | 保证每轮状态不同 | |
| PC-2 | 56 | 48 | 压缩 + 置换 | 生成最终子密钥$K_i$ |
DES存在8个弱密钥和12个半弱密钥,DES的密钥太短导致被淘汰
分组密码运行模式
分组密码工作模式的有:ECB (电子密码本)、CBC (密码分组链接)、CFB (密码反馈)、OFB (输出反馈)
CBC(密码分组链接)模式:加密算法的输入是当前明文组与前一密文组的异或
会自己画图!

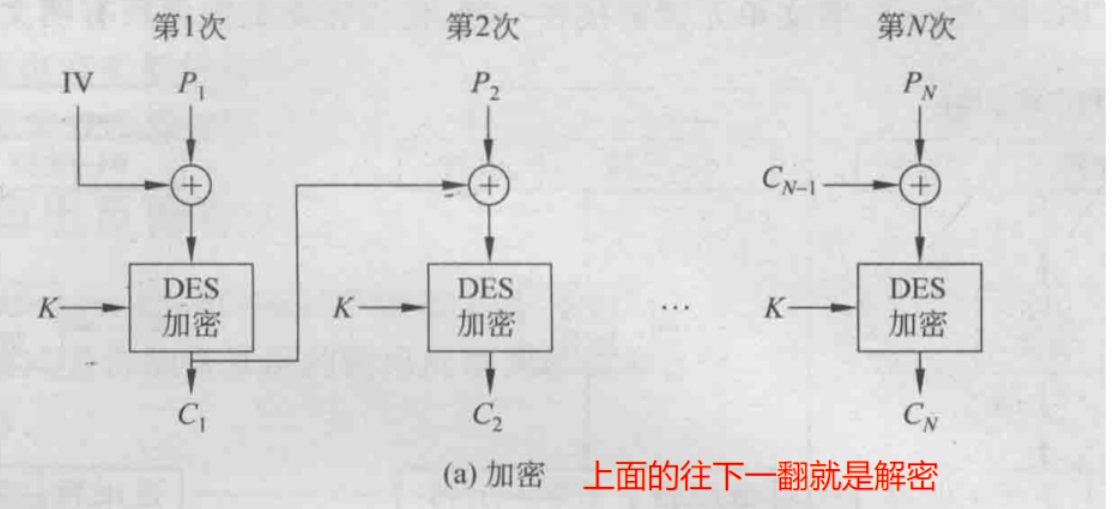
加密: Ci= Ek[Pi⊕Ci-1]
AES
1)分组长度只能是128位,密钥长度均能分别指定128位、192位、256位。
2)输入分组是以字节为单位的正方形矩阵
3)轮数不固定,取决于密钥长度(10/12/14),在 AES-128 中,算法共进行 10轮迭代
AES轮函数包括字节代换、行移位、列混合、轮密钥加,它是并行处理的,加解密不完全对称。最后一轮没有列混淆。
字节替换:它的构造是基于 有限域 $GF(2^8)$ 上的乘法逆元 ,然后再进行一个仿射变换 。目的是提供最强的非线性混淆。
行移位:每一行循环左移的位数是递增的 (0, 1, 2, 3 个字节) 。目的是提供扩散 (Diffusion)
列混合:它是对 State 矩阵的每一列进行矩阵乘法,运算域在 $GF(2^8)$ 上 。目的是在列方向上快速扩散

 AES算法很快且需要内存不多,十分可靠。
AES算法很快且需要内存不多,十分可靠。
多项式运算
加法和乘法
在GF(2^8)上的加法定义为二进制多项式的加法,等同于按位异或运算。




求逆

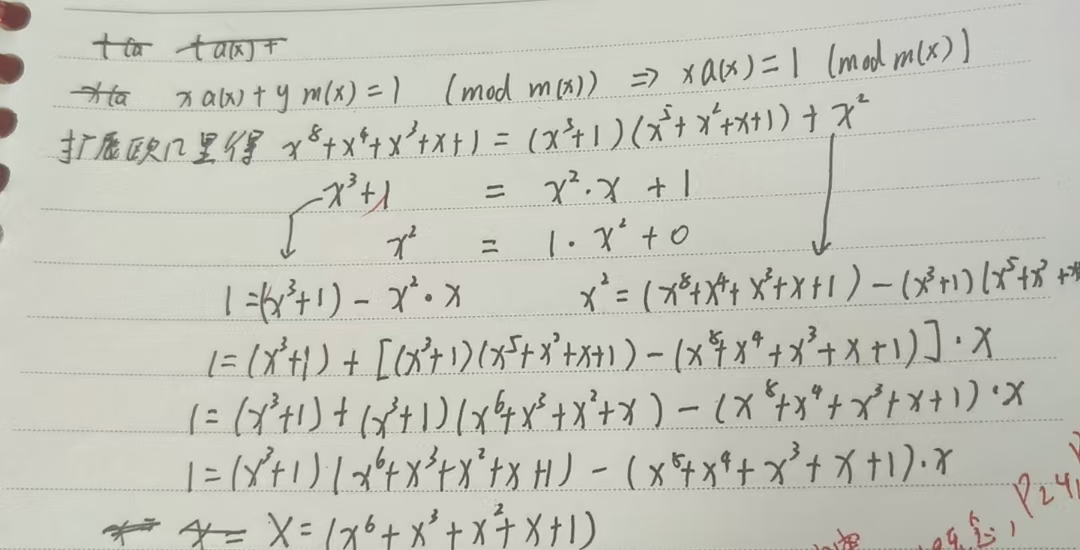
公钥密码学(重点)


公钥密码的速度慢。
RSA


密钥生成过程(背下来):


三种攻击RSA的方法:强力枚举密钥、数学攻击、时间攻击
密钥大小取在1024-2048位比较合适,不动点至少有9个。
RSA 算法中可能存在的安全隐患:
- $p,q$太小容易分解;$e,d$ 不能太小;需防共模攻击。
DH密钥交换
1)不能用于交换任意的信息,只限于进行公共密钥的建议,只对通信双方已知。
2)存在中间人攻击,DH 协议没有身份认证
3)数学原理:
- 公开参数:大素数$p$,本原根$g$。
- 私钥:Alice 生成$x_A$,Bob 生成$x_B$。
- 公钥 (混合后的颜色):
- Alice 发送:$Y_A = g^{x_A} \pmod p$
- Bob 发送:$Y_B = g^{x_B} \pmod p$
- 计算共享密钥$K$:
- Alice 计算:$K = (Y_B)^{x_A} \pmod p$
- Bob 计算:$K = (Y_A)^{x_B} \pmod p$
- 原理:$(g^{x_B})^{x_A} = g^{x_B x_A} = g^{x_A x_B} = (g^{x_A})^{x_B}$
EIGamal密码
例题:
在 ElGamal 加密系统中,素数 $p = 11$,本原根 $g = 2$。
- 密钥生成:假设接收方 Bob 选择的私钥是$x = 3$,请计算他的公钥$y$。
- 加密:发送方 Alice 想发送明文$M = 5$,她选择的随机数$k = 4$。请计算密文$(C_1, C_2)$。
- 解密:Bob 收到密文后,如何利用私钥解密还原明文$M$?(写出计算过程)
第一步:密钥生成 (求公钥$y$)
- 公式:$y = g^x \pmod p$
- 代入数值:
- $g = 2, x = 3, p = 11$
- $y = 2^3 \pmod{11}$
- $y = 8 \pmod{11} = 8$
- 结果:Bob 的公钥是$(y=8, g=2, p=11)$,私钥是$x=3$。
第二步:加密 (求密文$C_1, C_2$)
Alice 要发送消息$M=5$,随机数$k=4$。她需要计算两个值。
1. 计算$C_1$ (临时公钥)
- 公式:$C_1 = g^k \pmod p$
- 计算:
- $C_1 = 2^4 \pmod{11}$
- $2^4 = 16$
- $16 \div 11 = 1 \dots 5$
- 结果:$C_1 = 5$
2. 计算 masking key (共享秘密$K$)
- 公式:$K = y^k \pmod p$(用 Bob 的公钥$y$和随机数$k$)
- 计算:
- $K = 8^4 \pmod{11}$
- 这里有个口算技巧:$8 \equiv -3 \pmod{11}$
- 所以$8^4 \equiv (-3)^4 \equiv 81 \pmod{11}$
- $81 \div 11 = 7 \dots 4$
- (或者一步步算:$8^2=64 \equiv 9$,$9^2=81 \equiv 4$)
- 结果:$K = 4$
3. 计算$C_2$ (隐藏后的密文)
- 公式:$C_2 = M \times K \pmod p$
- 计算:
- $C_2 = 5 \times 4 \pmod{11}$
- $C_2 = 20 \pmod{11}$
- $20 \div 11 = 1 \dots 9$
- 结果:$C_2 = 9$
最终密文:Alice 发送$(C_1=5, C_2=9)$。
第三步:解密 (还原明文$M$)
Bob 收到了$(5, 9)$,他只有私钥$x=3$。
1. 恢复共享秘密$K$
- 公式:$K = (C_1)^x \pmod p$
- 原理:$(g^k)^x = g^{kx}$,和加密时算的$y^k$ 是一样的。
- 计算:
- $K = 5^3 \pmod{11}$(这里的 5 是$C_1$)
- $5^2 = 25 \equiv 3 \pmod{11}$
- $5^3 = 5^2 \times 5 \equiv 3 \times 5 = 15 \pmod{11}$
- $15 \div 11 = 1 \dots 4$
- 验证:算出来的$K=4$,跟加密时的一样!
2. 计算$K$的逆元 ($K^{-1}$)
- 我们需要把$C_2$里的$K$ “除掉”。在模运算里,除法就是“乘以逆元”。
- 目标:找到一个数$z$,使得$K \times z \equiv 1 \pmod{11}$。
- 代入:$4 \times z \equiv 1 \pmod{11}$。
- 试数:
- $4 \times 1 = 4$
- $4 \times 2 = 8$
- $4 \times 3 = 12 \equiv 1 \pmod{11}$ ✅
- 结果:$K^{-1} = 3$。
3. 还原明文$M$
- 公式:$M = C_2 \times K^{-1} \pmod p$
- 计算:
- $M = 9 \times 3 \pmod{11}$(这里的 9 是$C_2$)
- $M = 27 \pmod{11}$
- $27 \div 11 = 2 \dots 5$
- 结果:$M = 5$。解密成功! 🎉
记住:
- 加密算$K$用的是公钥$y$:$y^k$。
- 解密算$K$用的是$C_1$和私钥$x$:$C_1^x$。
- 如果你记混了,只要记住:解密必须用到私钥$x$。
ECC
基于什么数学难题?
- RSA基于:大整数分解问题 (Integer Factorization)。
- Diffie-Hellman / ElGamal基于:离散对数问题 (DLP)。
- ECC基于:椭圆曲线离散对数问题
更短的密钥长度,提供同等的安全性。ECC 使用的密钥长度远小于 RSA。存储空间占用更小,且带宽要求更低。


伪随机数生成器
生成方法:取中法、移位法、同余法(异曲同工)
哈希函数
Hash函数的主要功能是提供有效的数据完整性检验。
将任意长度的信息映射成较短的、固定长度的一个值。单向性、伪随机性。
应用:消息认证;数字签名




RSA 非对称加密速度慢,直接加密大文件效率极低。Hash 得到的摘要很短,签名速度快
生日悖论


两大主流算法:MD5 vs SHA-1
MD5以512位的分组长度来处理消息,每一个分组又被划分为 16个32位的子分组。
算法的输出由4个32位的分组组成,它们串联成一个128位的 消息摘要。
| 特性 | MD5 | SHA-1 |
|---|---|---|
| 输出长度 (摘要) | 128 位 | 160 位 |
| 安全性 | 较弱 (已被王小云破解) | 较强 (但也已被破解) |
| 运算轮数 | 4 轮 (每轮 16 步,共 64 步) | 4 轮 (每轮 20 步,共 80 步) |
| 缓冲区 | 4 个寄存器 (A,B,C,D) | 5 个寄存器 (A,B,C,D,E) |
| 速度 | 更快 | 稍慢 |
| 字节序 | 小端 (Little-endian) | 大端 (Big-endian) |
数字签名
MAC是共享密钥,不能抗抵赖,签名才可以
数字签名 (为了认证):你用私钥签名 (加密),别人用你的公钥验证 (解密) 。
三大功能:
- 身份认证 (Authentication):确认消息确实是由签名者(持有私钥的人)发送的。
- 数据完整性 (Integrity):确认消息在传输过程中没有被篡改(因为 Hash 值变了,签名就对不上了)。
- 不可否认性/不可抵赖性 (Non-repudiation):发送方不能抵赖说“这不是我发的”,因为私钥只有他有。
1)RSA 签名
- 原理:基于大整数分解难题。
- 公式 (稍微记一下,和 RSA 加密反过来):
- 签名:$s = m^d \pmod n$ (用私钥 $d$)
- 验证:验证 $m$ 是否等于 $s^e \pmod n$ (用公钥 $e$)
2)ElGamal 签名
- 原理:基于离散对数难题。
- 重要考点:它引入了一个随机数$k$。
- 陷阱:每次签名的随机数 $k$ 必须不同!如果重复使用 $k$,攻击者可以直接算出私钥 $x$ 。
- 缺点:生成的签名长度较长(是消息的两倍),效率不如 RSA 。
3)Schnorr 签名
- 特点:比 ElGamal 更短、更快。
- 优势:因为它计算量小,特别适合智能卡这种计算能力弱的设备
练习题


子密钥:每轮使用一个 48 位子密钥 KiK_iKi(由 56 位有效主密钥通过 PC-1、循环左移、PC-2 得到)。
描述说明 DES 算法的加解密过程(也可以画图说明)
DES 是一种 64 位分组对称加密算法。其输入密钥为 64 位,其中 8 位为奇偶校验位,经PC-1去除后得到 56 位有效密钥。该 56 位密钥经过循环左移和PC-2 压缩置换,产生 16 个 48 位轮密钥。
64位明文经初始置换IP 后得到 L₀、R₀。随后进行 16 轮 Feistel 运算:每轮中对 R₍ᵢ₋₁₎ 进行E扩展置换 → 与 Kᵢ 异或 → 通过 8 个 S 盒压缩至 32 位 → P 置换,得到 F(R₍ᵢ₋₁₎, Kᵢ)。更新为 Lᵢ=R₍ᵢ₋₁₎,Rᵢ=L₍ᵢ₋₁₎⊕F。
16 轮结束后交换左右,再经逆初始置换IP⁻¹ 得到 64 位密文。
以 DES 为例,画出分组密码的密码分组链接(CBC)模式的加密解密示意图,假设加密时明文一个比特错误,对密文造成什么影响,对接收方解密会造成什么影响?

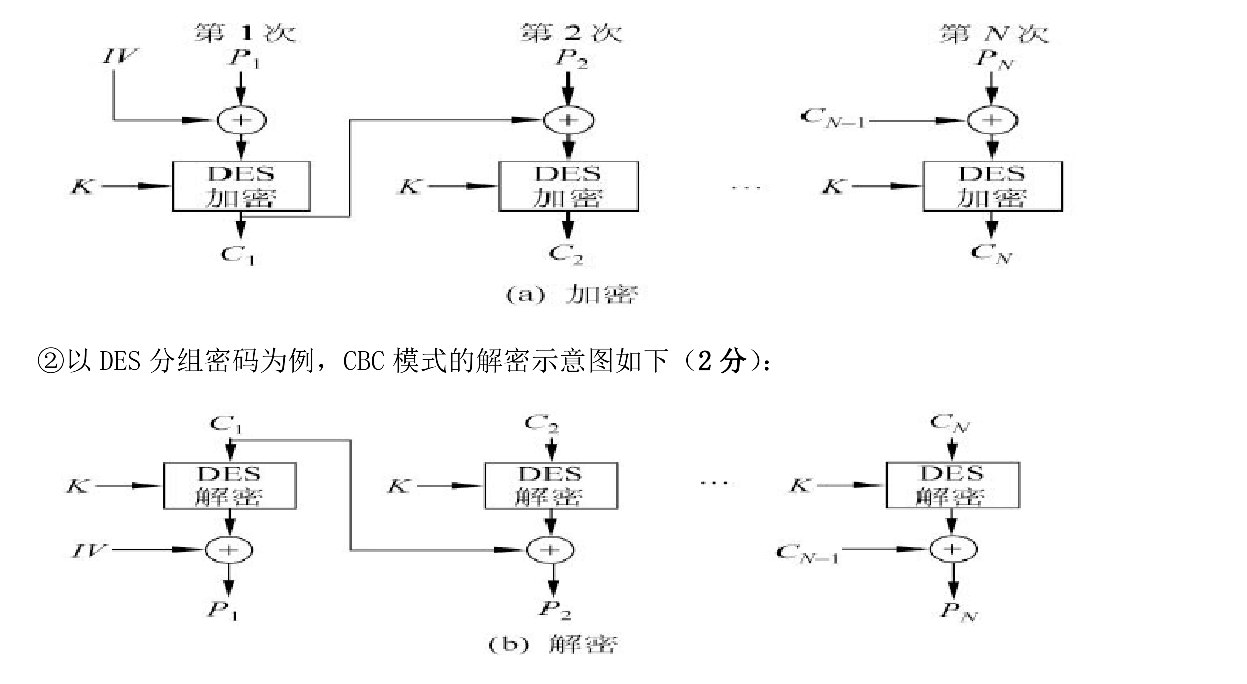
加密时明文的一个比特错误,会导致该组加密密文发生变化,然后这个错误反馈值会作为下 一次 DES 加密的输入值,再经过 DES 加密变换,会导致后面的密文都受到影响。
对 于接收方来说,加密明文的一个比特错误,只会影响对应明文块所产生的密文的正常解密,其他数据块可以正常准确地解密。
请设计一个基于 Hash 函数和 RSA 签名的安全分发流程。
流程:
发送方:Hash(文件) -> 摘要 -> 用私钥加密摘要(签名) -> 发送(文件+签名)。
接收方:分离文件和签名 -> 用公钥解密签名得摘要H1 -> Hash(文件)得摘要H2 -> 对比 H1 和 H2。
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 77 浏览
- ZK 编年史:电路(第二部分) 136 浏览
- 有限域之美与力量 (以及 Zig) 263 浏览
- 扳手攻击:发生与预防 315 浏览
- zkEVM 安全性概览 351 浏览
- 基于哈希函数的签名(三):多次签名 481 浏览
- 基于哈希函数的签名(二):少量次数签名 555 浏览
- Zig 签名(Ed25519 和 ECDSA) 747 浏览
- ZK Mesh:2025年12月回顾 493 浏览
- (Z/nZ)*——Z/nZ的乘法群 639 浏览
- 从零开始构建 ZK (STARK) 证明器的旅程 706 浏览
- 发布L1 zkEVM #2:安全基础 701 浏览

