椭圆曲线深入研究（第10部分）

我想，你能来到这里一定不容易，我亲爱的读者。

我们已经完成了九篇完整的文章的椭圆曲线理论，涵盖了从最基础的到一些非常抽象的内容（比如，除子divisors ）。

现在是我们更熟悉一些实际方面的时候了。特别是，我认为该系列缺失的是展示一些在最常见算法中使用的实际曲线。

在这样做的过程中，我们将涵盖一些我们还没有机会看到的很酷的概念，这将很好地结束我们的椭圆曲线之旅。

我们快到了！坚持住，只剩下最后的冲刺了。

SECP 家族

我们今天的故事从一个家族曲线开始，这个家族是世界上部署和使用最广泛的曲线之一。事实上，当你的浏览器连接到这个网站时，很可能就使用了其中一种！

这个名字来源于定义它们的文档，高效密码学标准。而 p 与定义曲线的素数域有关。

由于它们如此普遍，所以它们是一个很好的起点。有多种变体可用，但我们这里只看其中一种。

比特 coin 曲线

曲线 secp256k1 是比特 coin 和以太坊都使用的曲线。

实际上，这是一个非常简单的曲线。它的 Weierstrass 形式就是：

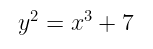
y² = x³ + 7

然而，我们完全知道，定义一个椭圆曲线不仅仅是指定它的公式：我们还需要定义我们将要操作的素数域，并且我们需要找到一个大型循环子群的合适的生成器。

让我们从素数域开始。在这里：

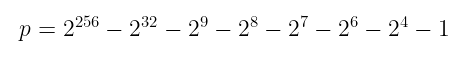
p = 2^{256} — 2^{32} — 2⁹ — 2⁸ — 2⁷ — 2⁶ — 2⁴ — 1

当我看到这个数字时，我的第一反应是“嗯，这真是非常特别”。这种数字会让你怀疑是否有什么更深层的原因，至少我个人是这么觉得的。

当然，这种特定结构是有充分理由的。这个数字本身属于一个叫做 Solinas 素数（或 广义梅森素数）的家族，它们的主要优点是能够进行快速模约简，至少与一些随机的 256 比特素数相比是这样。

简单来说，请注意我们可以将 p 表示为 2²⁵⁶ - c，其中 c 是一个与 p 相比“很小”的常数。有了这个，很容易看出 2²⁵⁶ mod p = c。

所以策略如下：将任何你想约简的大数（比如，512 比特）分成 高位( xₕ) 和 低位( xₗ)。我们可以将任意数字 x 的这种分离表示为 x = xₕ * 2²⁵⁶ + xₗ。当我们对表达式应用 mod p 时，我们会得到一些非常棒的东西：x mod p = xₕ * c + xₗ。

而且由于 c 很小（并且还有一个稀疏的二进制表示，但我们现在先不用担心），所以这个操作非常快！

素数域，搞定！现在我们将注意力转向群结构，从它的阶（元素数量）开始，也就是这个小小的数字：

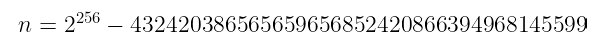
n = 2^{256} — 432420386565659656852420866394968145599

你可能会问，这有什么特别之处？听好了：这是一个素数。你知道这意味着什么吗？感谢 拉格朗日定理，我们可以确定整个群是一个单一的循环群，其中每个非单位点都会完全生成该群。

啊，真好

从安全的角度来看，这是理想的。其他较小子群的存在为某些攻击向量打开了大门，例如众所周知的 Pohlig-Hellman 算法。

所以，理论上，我们可以选择任何点作为生成器。只是为了兼容性，一个“标准”生成器被选为该曲线的另一个参数。

你可以在这里查看它的值。

最后，还有一件事值得一提，那就是 secp256k1 中的 k。

Secp256k1 也属于 Koblitz 曲线 家族。这个家族的定义特性是它们具有可有效计算的自同态。如果你想深入了解这个主题，有很多材料，所以我只给你一个大概的概念。

正如我们已经提到的那样，自同态是将 E（曲线）映射到自身的函数。所以我们本质上有一个映射 φ，它作用于曲线点，满足 φ (P) = λP，其中 λ 是某个常数。

这一点很重要，因为它可以使用一种叫做 Gallant-Lambert-Vanstone 分解法（或简称 GLV）的方法来实现更快的标量乘法。

你可以将标量 k 分解为两个较小的标量（ k₁ 和 k₂），而不是使用标准的 double-and-add 乘法来找到 [k]P，这样：

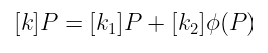
[k]P = [k_1]P + [k_2]\phi(P)

两种乘法都可以并行计算，然后加在一起。

实际上，速度提升非常显著——比标准标量乘法快大约 25-30%。对于执行数百万次 ECDSA 操作的系统来说，这加起来就很可观了。但是，正确实现 GLV 非常棘手，如果做得不小心，可能会引入侧信道攻击（计时）。

在实践中，许多库都不屑于这样做。但对于高性能场景（比如区块链节点每秒验证数千个签名），GLV 自同态可能是一个有价值的优化。

所有这些特殊特性可能是中本聪这个神秘人物选择 secp256k1 而不是更标准的选择（比如 secp256r1）的原因。它很简单，而且在需要时速度很快。有些人还推测，中本聪也避免使用 NIST 曲线（又名标准曲线），因为担心它们可能存在潜在的后门。

尤其是在 Dual_EC_DRBG 争议 之后。

我们可能永远不会真正知道。我们所知道的是，这条小小的曲线，凭借其所有隐藏的技巧，负责保护价值数千亿美元的加密货币。至少在短期内，它不会消失！

替代形式

到目前为止，我们已经在它们的短 Weierstrass 形式中概念化和呈现了曲线：

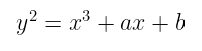
y² = x³ + ax + b

这是“标准”表示。这是大多数人在听到“椭圆曲线”时想到的。但正如我们在该系列的第一篇文章中暗示的那样，这并不是椭圆曲线可以采取的唯一形式。

事实上，我们当时还提到了另外几种形式，其中一种我现在想正式地介绍给你。认识一下 Montgomery 形式：

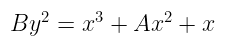
By² = x³ + Ax² + x

它有所不同，但同时，它也不是那么陌生。毕竟，你只有这么多种方法可以写三次多项式！

我们现在有了一个 y² 的系数，和一个新的 x² 项。总的来说，这种变化似乎不是很剧烈。

Curve25519 就是以这种形式定义的一条曲线，它的方程是：

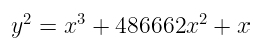
y² = x³ + 486662x² + x

并且定义在素数域 p = 2²⁵⁵ - 19 上。

与 secp256k1 的情况非常相似，这个素数值得我们赞赏一下。这是一个非常简单的数字，它也是一个伪梅森素数。这有助于使用类似于之前介绍的快速模约简的技术来快速进行模算术。

我知道你现在在想什么。嘿，Frank，为什么要有不同的形式？它会改变什么？

Montgomery 形式有一个非常好的特性，它具有非常有趣的含义：标量乘法 只需要使用 x 坐标。点倍增的显式公式如下所示：

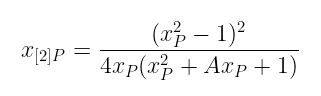
x_{[2]P} = \frac{(x_P² — 1)²}{4x_P(x_P² + Ax_P + 1)}

点加法有点棘手。虽然它可以用 x 坐标来完成，但一切都真正地汇集到一个叫做 Montgomery 阶梯的算法中，我们将在稍后看到它。

在此之前，让我们谈谈只跟踪一个坐标的主要优点：

• 在速度方面，我们大约有一半的数据需要处理。这使得 Montgomery 阶梯比常规的 Weierstrass 乘法快大约两倍。
• 带宽 也受益于这种形式，因为我们只需要发送 x 坐标（对于 Curve25519 来说是 32 字节），而不是完整的点。这实际上就是协议 x25519（Diffie-Hellman 密钥交换）所做的。
• 最后，Montgomery 阶梯算法在其执行过程中非常规律，这意味着它执行的操作数量不依赖于用于乘法的标量模式。这使得它自然能够抵抗一种叫做计时攻击的攻击，这种攻击试图通过测量执行算法所花费的时间来猜测有关标量的信息。

并且 Weierstrass 实现历史上一直在这方面挣扎。

这听起来很棒。那么这个神奇的算法是关于什么的呢？

Montgomery 阶梯

实际上，这个算法非常简单。

要计算 [k]P，你只需要跟踪两个值：R₀ 和 R₁。这些点将满足一个特殊的不变式：R₁ - R₀ = P。我们将在稍后看到为什么这很重要。

从 R₀ = 𝒪（在 Montgomery 形式中表示为 x = 0）和 R₁ = P 开始，我们逐位地遍历 k。也就是说，我们取 k 的二进制表示，然后从最低有效位到最高有效位遍历它的数字，执行这些更新：

• 如果该位是 0：R₁ ← R₀ + R₁，然后 R₀ ← 2R₀
• 如果该位是 1：R₀ ← R₀ + R₁，然后 R₁ ← 2R₁

我们可以立即看到几件事。首先，不变式 确实成立——你可以通过几个例子自己检查一下。其次，两个分支都完全执行一个加法和一个倍增。执行模式是相同的，所改变的是哪个变量获得每个更新。这就是我们之前提到的恒定时间属性，也是为什么它能够抵抗计时攻击的原因。

最后，我们需要处理加法——这就是魔力发生的地方。两个点 U 和 V 的加法的显式公式是这个：

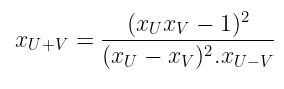
x_{U+V} = \frac{(x_U x_V — 1)²}{(x_U — x_V)².x_{U-V}}

有些东西应该立即引起你的注意：我们需要点 U - V 的 x 坐标。在正常情况下，这并没有多大意义——一个依赖于另一个加法的加法（减法只是加法 - V）似乎是一个不可能的漏洞，也是一个灾难的根源。

但这就是我们的不变式发挥作用的地方：当添加 R₀ 和 R₁ 时，我们确切地知道这个差值是什么：P！

非常迷人，不是吗？

剩下的呢？

没错。这个算法看起来很酷。但是我们精心定义的群律呢？甚至更糟的是，我们所经历的所有除子理论呢？这不再重要了吗？

别慌——当然重要！

Montgomery 形式只是一种不同的方式来表示也可以用 Weierstrass 形式编写的曲线。事实上，有一种转换允许一个系统被转换为另一个系统，反之亦然。

自己尝试一下：你可以使用映射 (x,y) ↦ (x/B + A/3B, y/B) 从 Montgomery 形式转换为 Weierstrass 形式。另一种方式有点棘手，但这应该足以说服你！

所述的转换本质上是一种坐标变换——一种保持曲线代数结构的双有理映射。群律保持不变，除子保持不变，我们研究的基本性质都成立。

这类似于用笛卡尔坐标与极坐标描述同一个几何对象。对象本身不会改变——你只是以不同的方式看待它。

那么定义点加法的那些线相交呢？仍然存在。

除子呢？仍然存在。

群结构呢？仍然存在。

Montgomery 形式只是允许更有效的标量乘法。理论并没有改变——只有计算改变了。

Edwards 曲线

Curve25519 非常适合大量使用标量乘法的协议，例如 Diffie-Hellman 密钥交换。但这并不意味着它们是万能的。

例如，数字签名算法 需要点的加法而不是标量乘法。理想情况下，我们还需要快速验证和统一的执行时间，而不管执行的操作如何。

在这种情况下，Montgomery 曲线很挣扎，因为只有当我们有一个不变式时，加法才有意义。

至于 Weierstrass 形式，问题是我们需要一个完整的加法公式——换句话说，一个对所有点类型都完全相同的公式。由于存在一个叫做无穷远点（𝒪）的小麻烦点，这在 Weierstrass 形式中根本不可能。

我们需要一个替代方案。这就是 _扭曲 Edwards 形式_出现的地方。

扭曲 Edwards 形式

一个扭曲 Edwards 曲线方程看起来像这样：

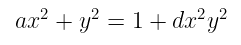
ax² + y² = 1 + dx²y²

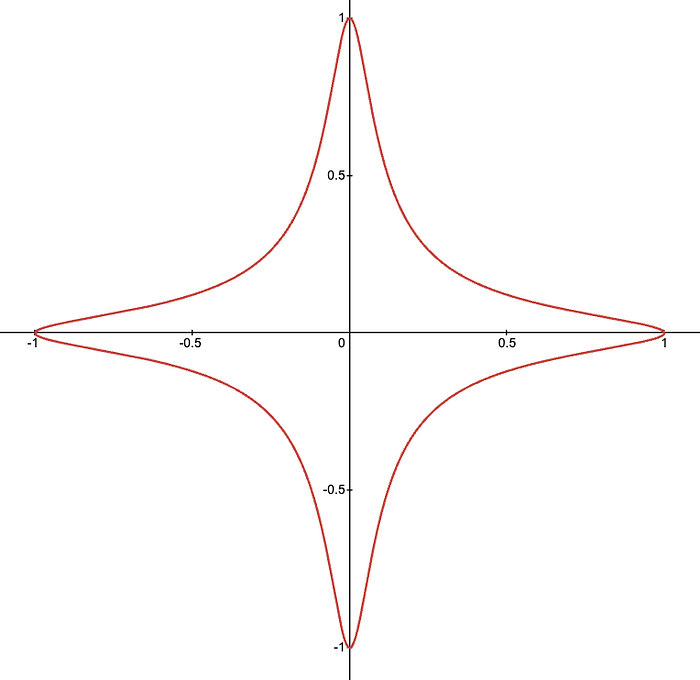
当绘制它们时，它们看起来很奇怪！

在出现任何混乱之前，我必须澄清：这里的 扭曲 与 曲线扭曲 无关，就像我们之前在该系列中讨论过的那样。这只是一个不幸的命名选择。

扭曲 Edwards 只是这种曲线形式的名称，将其与 Harold Edwards 在 2007 年提出的原始 Edwards 曲线区分开来（原始 Edwards 曲线具有 a = 1）。“扭曲”只是意味着我们添加了参数 a 来 推广 原始形式。

解决了这个问题，我们可以专注于这种形式所能提供的东西。

正如之前暗示的那样，扭曲 Edwards 曲线的突出特点是它们完整的加法公式。在扭曲 Edwards 形式中，点加法由下式给出：

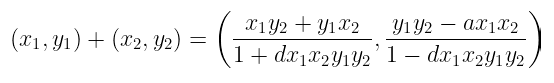
(x_1, y_1) + (x_2, y_2) = \left(\frac{x_1y_2 + y_1x_2}{1 + dx_1x_2y_1y_2}, \frac{y_1y_2 — ax_1x_2}{1 — dx_1x_2y_1y_2}\right)

仔细看看这个公式。注意到什么有趣的东西了吗？

乍一看，可能没有。但是如果我告诉你尝试将 P 加到它自身呢？这个公式似乎能够很好地成立。那么单位元呢？在这种坐标系中，单位元是点 (0,1)——你可以自己检查一下——，并且上面的公式也有效。

这正是扭曲 Edwards 曲线上的加法的威力：没有特殊情况。这个公式是完整的，因为它只需要适用于 所有输入！

将此与 Weierstrass 形式进行对比，在 Weierstrass 形式中，我们必须处理几个不同的情况：

• 如果 P = 𝒪，那么 P + Q = Q
• 如果 Q = 𝒪，那么 P + Q = P
• 如果 P = -Q，那么 P + Q = 𝒪
• 如果 P = Q，使用切线（点倍增）
• 否则，使用通过 P 和 Q 的线

这需要五个不同的情况 需要单独检查和处理，其中两个需要不同的公式。

拥有一个单一的、完整的公式有一些优点：

• 最明显的是它的 简单性。更少的分支意味着更少的错误机会。当处理加密代码时，一个错误可能会导致灾难，这种简单性非常宝贵。
• 其次，由于我们始终执行相同的操作，因此我们获得了 恒定时间的执行。与 Montgomery 曲线非常相似，这提供了对计时攻击的抵抗力。
• 最后，这个公式对于两个操作数来说都是 对称 和 高效 的。特别是对于签名验证，你需要计算点的线性组合（类似于 [s]G + [h]P），拥有快速、统一的加法会产生真正的影响。

与 Montgomery 曲线相比，权衡是你所期望的：标量乘法没有那么快。但这完全可以接受——我们选择哪条曲线很大程度上取决于我们将使用它们进行哪种类型的协议。

Ed25519

Ed25519 是最常用的扭曲 Edwards 曲线之一，它的形式是：

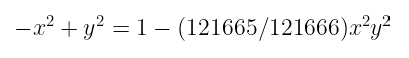
-x² + y² = 1 — (121665/121666)x²y²

小心！那里的除法是模 p！

该曲线定义在 p = 2²⁵⁵ - 19 上。这是一个熟悉的值——它与我们在 Curve25519 中使用的值相同。

这不是巧合。事实上，Ed25519 和 Curve25519 是双有理等价的——它们是相同的底层代数曲线，但以不同的坐标系表示。

就像我们之前看到的 Montgomery 和 Weierstrass 形式之间的关系一样！

因为我们基本上可以在两种形式中使用相同的曲线，所以我们可以针对我们的用例进行优化，并且仍然保留曲线提供的安全保证。甚至可以在形式之间转换点，在极少数情况下我们需要快速加法和快速标量乘法。

我认为这太棒了！

配对友好曲线

为了总结一下，让我们简单地谈谈专门为配对设计的曲线。

如果你还没有阅读本系列中关于配对的之前文章，我强烈建议你在跳到下一节之前先阅读它们！

在设计这种类型的曲线时，我们需要考虑一些额外的要求，例如：

• 我们需要一个大小为 r 的素数阶子群。
• 我们需要有一个嵌入度 k，使得 r 除以 qᵏ - 1，其中 k 足够小以提高效率，但又足够大以保证安全性。
• 以及我们根本没有讨论过的其他一些条件，比如保证 扭曲安全性。

找到满足这些条件的曲线不是一件容易的事。例如，如果你选择一些随机曲线，那么嵌入度很可能非常大——实际上接近于群的阶——这使得在这些曲线上进行配对完全不切实际。

为了使这一点绝对清楚，请记住我们在域扩展上执行操作。嵌入度告诉我们需要存储多少个基本域的元素才能表示扩展中的单个元素。并且随着 k 的增长，操作变得 指数级地更加昂贵，以至于完全无法管理。

那么我们如何去寻找这些难以捉摸的曲线呢？

复数乘法方法

构造配对友好曲线的主要技术被称为复数乘法 (CM) 方法。

CM 方法不是生成随机曲线并祈祷它们具有正确的属性，而是向后工作：我们指定我们想要的属性（嵌入度、安全级别等）并解决某个问题以找到实现这些目标的曲线参数。

所述问题来自我们还没有真正深入探讨的一个领域，尽管我们确实提到了一些关于它的事情：椭圆曲线上自同态的研究。

有些曲线比标准标量乘法、Frobenius 自同态（及其幂）具有更多的可用自同态。当发生这种情况时，该曲线被称为配备了 复数乘法。

它的名称是这样的，因为我们可能会找到一个满足类似于 φ² + D = 0 （在自同态环中）条件的自同态。这类似于满足 i² + 1 = 0 的复数 i，因此得名！

只有当曲线满足一个特殊关系（CM 方程）时，才会发生这种情况，由下式给出：

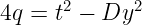
4q = t² — Dy²

其中 q 是域的大小，t 是 Frobenius 迹——简单地定义为这个差：

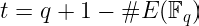
t = q + 1 — \#E(\mathbb{F}_q)

在这种情况下，拥有一个额外的约束实际上是 有益的：这意味着我们可以 系统地搜索 具有我们需要属性的曲线。

该过程大致如下：

1. 选择你的目标嵌入度 k
2. 选择一个小的判别式 D。较小的 D 值更容易处理，并且它们通常取像 D = 1, 2, 3, 7, 11 等值。
3. 求解 CM 方程，得到 y 的不同值，得到对 (q, t).
4. 检查 q + 1 - t 是否有一个大的素数因子 r。这将保证存在一个阶为 r 的子群。
5. 验证 r 是否除以 qᵏ - 1。这确保了嵌入度正好是 k（或 k 的一个因子）。
6. 检查 q 是否为素数（或素数幂）。回想一下 q 定义了我们的域。

如果我们能够满足所有这些条件，那么我们就会偶然发现一个配对友好的曲线！很简单，对吧？

请注意，曲线方程本身（y² = x³ + ax + b 中的 a 和 b 值）可以有点随意地选择，只要该曲线具有正确的点数（以获得所需的 Frobenius 迹）。

这真的只是这个主题的冰山一角。我们不会深入到任何进一步的细节，因为它是一个非常深的兔子洞，通向 代数数论 和 类域论。

我很想说“这远远超出了我的能力范围”，但我这样做是免费的，所以…

此外，我们需要知道如何 计算曲线上的点 ——这是另一个有趣的努力，我留给你自己去探索。

最重要的是，我们对其他属性感兴趣，例如扭曲安全性、高效的算术以及避免某些攻击向量。简而言之：

寻找配对友好的曲线非常困难。

因此，密码学家选择定义一些参数族，而不是每次都解决 CM 问题。这些公式为任何所需的安全级别生成合适的曲线——如果愿意，可以将其看作是精选的快捷方式。其中一些最重要的包括：

• Barreto-Naehrig (BN): k = 12，高效。
• Barreto-Lynn-Scott (BLS): k = 12、24 或 48，并且比 BN 具有更好的安全性。
• Kachisa-Schaefer-Scott (KSS): k = 18，效率和安全性之间的中间地带。

这些是用于推导一些最广泛使用的配对友好曲线的方法，其中我们可以找到 BLS12–381 和 BN254。

在撰写本文时，BLS12–381 是基于配对密码学的当前黄金标准。它来自具有 k = 12 的 BLS 家族，定义在 381 比特的素数域上。曲线方程非常简单：

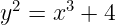
y² = x³ + 4

它被 以太坊 2.0、Zcash、Filecoin 等巨头使用，并且也被用于大多数现代零知识证明系统中。

总结

所以，是的——虽然我们已经学习了很多理论，但我希望我们停下来片刻，欣赏一下还有多少东西有待发现。

事实上，我们为椭圆曲线定义的大多数东西都可以推广到 代数簇 的研究中。

总而言之，椭圆曲线是美丽的结构，它们在看似无害的外表下隐藏着惊人的复杂性。

它们以令人难以置信的优雅将数学的不同领域结合在一起，并在计算效率和安全性之间实现了出色的平衡。 由于量子计算机的威胁，人们认为椭圆曲线密码学很快就会过时，并将被当前正在测试和开发的后量子算法的激增所取代。但短期来看，ECC 不太可能消失，可能就像我们今天仍然看到 RSA 被使用一样，我愿意打赌它会在很长一段时间内存在。

这就是本系列的全部内容！

我不认为自己是这方面的专家。事实上，在撰写这些文章的过程中，我可能学到了和你一样多的东西，因为每篇文章都花费了大量的研究精力，尤其是在那些我感觉这些想法没有完全在我脑海中点击的时候。

我希望你觉得这些材料有用，甚至有趣和引人入胜。如果你发现这个话题很有趣，我想鼓励你不要止步于此 —— 有很多很棒的书籍对椭圆曲线进行了更深入的介绍。

如果有什么事，你知道在哪里可以找到我！

干杯！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～