椭圆曲线深入研究（第八部分）

在经历了穿梭于 挠群 的复杂丛林之后，我们将继续我们的 配对 之旅。

正如我上次提到的，这是关于这些迷人结构的三部分系列文章的第二部分。

但是，我们需要的不仅仅是之前的文章。事实上，我们需要之前 几篇 文章中讨论的所有内容，因为 除子 在配对定义中也起着至关重要的作用。

事情不会变得更容易，所以我建议在需要时放慢速度，真正给这些概念时间去理解。

这不会很顺利，但我们会到达目的地的。

欢迎登上配对快车。我将担任你的向导。

预备知识

在我们介绍本文将要探讨的 两个配对 之前，我们需要先了解一些内容——用于两个配对定义中的几个原则。

当我们讨论除子时，我们讨论的主要概念之一是 主除子。这些表示 函数 的除子，并具有两个定义的特征：

• 一是点的重数（nₚ 值）加起来为零，或者除子的 度 为 0。
• 另一个我们尚未提及的是：

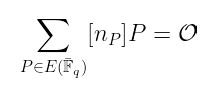
这是 阿贝尔-雅可比定理 的一个结果，它非常复杂，我们现在还不想涉及。它涉及有趣的拓扑概念，我们将来可能会探索！

这意味着对于某个整数 m，我们可以构造一个函数 fₘ,ₚ，它具有以下除子：

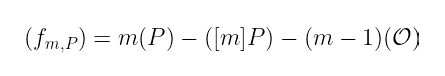
显然，这是一个主除子，因为重数之和为零（它的度为零），并且因为 [m]P - [m]P 显然是 𝒪。

如果我们选择 m = r，则此函数的除子简化为：

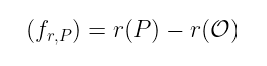
我们需要这个小除子来理解我们的配对定义！

评估一个除子

我们需要了解的另一件事是如何在除子上 评估一个函数。也就是说，给定一个函数：

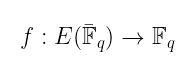
我们希望能够定义 f(D) 是什么，给定 D 是某个除子。

事实上，对此有一个非常自然的定义：

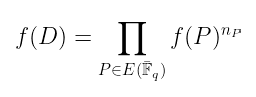
因为 f 只能将曲线上的点作为输入，所以我们没有更多选择！不过，我们很快就会亲眼看到这个定义非常方便。

说实话，这并不总是有效。为了使这有意义，我们需要施加一个额外的条件：（f） 和 D 必须具有 不相交的支撑。

回想一下，除子的 支撑 是具有非零重数的点的集合——这意味着它们要么是函数的 零点，要么是 极点（当然是在曲线上定义的，这意味着它们确实是交点，正如我们已经知道的那样）。

因此，如果 （f） 和 D 在它们的支撑中共享一个点，这意味着 f(P) 的某些值将为 0 或 无穷大 ——导致整个乘积要么坍缩为零，要么膨胀为无穷大。

通过不相交的支撑，我们确保 f(D) 将产生一些有意义的值！

好了，介绍结束了！感觉怎么样？

哦，天哪，还有更多吗？

是的，还有。有了这些，我们终于可以定义配对了。开始吧！

韦伊配对

我们已经知道配对是以下形式的函数：

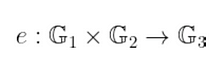
输入仅仅是曲线上的两个点 P 和 Q。但不是任何点——让我们将它们限制为 r-挠点。我们将在几分钟内看到原因。

我们知道的另一件事是，我们可以通过在处理 莫德尔-韦伊群 时定义的同构，轻松地将点映射到除子：

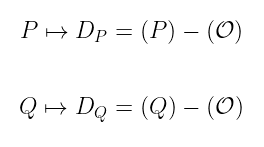
通过 除子等价 的概念，我们可以找到与 P 和 Q 相关的除子等价的除子，以使它们具有不相交的支撑。

考虑到这一点，韦伊配对 定义为：

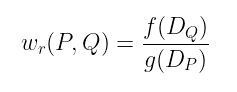
假设函数 f 和 g 具有除子：

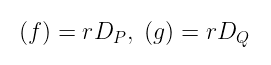
我知道。在经历了这么多的定义和深刻的数学之后，这可能会让人觉得有点平淡无奇。但这里肯定有很多东西需要解开……这个不起眼的外表肯定隐藏了很多东西！

仔细检查会发现一个问题：不满足 不相交的支撑 的要求。两个函数和两个除子在它们的支撑中共享一个点：𝒪。我们知道这意味着什么——配对将没有明确的定义。

看来我们遇到了麻烦。

腌黄瓜 Riiiick！

这次的技巧是什么？又是 除子等价！

只需要更新两个除子中的一个（以及它的关联函数，当然），但让我们看看如何更新两个除子，以保持公平。

我们在这里不歧视除子。

为此，我们选择曲线中的另外两个随机点 R 和 S，并遵循 此处 概述的相同过程。我们所做的只是使用我们值得信赖且有效的弦切律。作为复习，让我们看看它在 P 和 R 中的作用：

• 绘制穿过这些点的线。它将具有除数 ( 𝓁 ) = (P) + (R) + (-(P + R)) - 3( 𝒪 ).
• 绘制穿过 -(P + R) 的垂直线；这条线的除数当然是 v = (-(P + R)) + (P + R) - 2( 𝒪 ).
• 最后，我们只添加 (v) 并减去 (𝓁)：

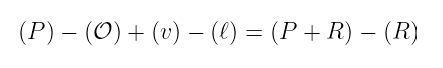
请注意，这些除数是 等价的，因为它们的差是一个函数的除数。

更新函数

但是 f 和 g 呢？我们已经更新了输入，是的，但整个问题的要点是为我们刚刚找到的这些新除数找到函数。

以原始的 f 为例。它是一个函数，使得：

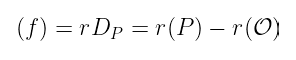
我们现在需要找到一些函数 f'，使得：

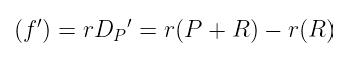
如果你眼光敏锐，你可能已经发现了与除数转换过程的相似之处——我们需要做的就是完全 r 次地应用该过程。

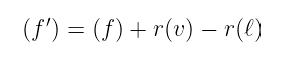
(f’) = (f) + r(v) — r(\ell)

令人惊讶的容易，我想说！

这个除数转换等效于将原始函数 f 乘以 v/ 𝓁 正好 r 次，所以：

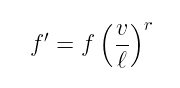
太棒了！现在我们有了计算配对所需的所有元素。

但是……我不知道你怎么想，但我 完全 不相信这个 w 函数是 双线性的。

韦伊互反律

你怀疑是绝对正确的——我们构建的表达式在没有任何进一步的上下背景下，看起来相当随意。

正如你所预料的那样，我们在这里缺少了 秘密香料。

你说香料了吗？

使这项工作起作用的魔力被称为 韦伊互反律，这是一个强大的定理，它指出对于椭圆曲线上的任何两个函数 f 和 g，以及它们的除数 (f) 和 (g)，以下成立：

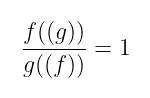
同样，一个简单、无害的表达式。然而，在底层，这告诉我们，函数“看到”彼此的除数的方式存在一些 基本对称性。

让我们不要在细节上过多纠缠。更令人兴奋的是它如何应用于配对定义。通过韦伊互反律，我们知道：

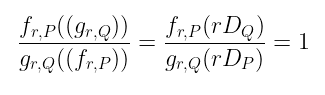
但是由于我们定义了函数对除数的评估方式，这实际上可以重写为：

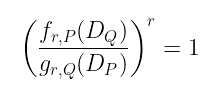
实际上，为了使其起作用，我们还需要 (𝒪) 的函数评估结果精确地为 1。这不一定是真的，但通常会涉及一个 归一化 过程来确保此条件。

同样重要的是要提到，此步骤是为什么使用 r-挠点至关重要——否则，我们将无法分解出 r！

好吧，韦伊，好吧……看看那个！它是我们的配对的 r 次方！这意味着我们的配对的输出仅仅是域中的 r 次单位根。

双线性性

但是这与双线性无关。

让我们更进一步。为了使我们的配对是双线性的，我们需要：

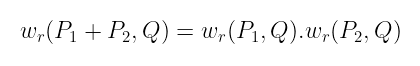
当然，我们需要证明它对两个输入都成立——但是对于我们省略的那个，可以提出类似的论点。

正如我们已经知道的那样，我们首先需要为第一个输入构造一个函数，其除数为 r(P₁​+P₂​) − r( 𝒪 )。幸运的是，有一种直接的方法可以做到这一点，而且同样是通过利用 弦切律。

你看，通过应用这个过程，我们得到以下除数等价性：

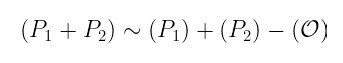
没有什么可以阻止我们将两边乘以 r：

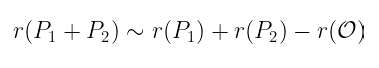
除数等价性仅表示这些除数彼此之间相差一个我们称之为 ϕ 的函数。如果我们从两边减去 r( 𝒪 )：

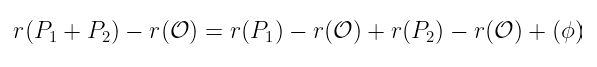
给你！那就是我们想要的除数。在函数除数方面，表达式映射到以下乘积：

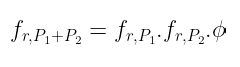
总而言之：要证明双线性性，我们只需要证明：

同样的机制再次适用：函数在除数上的求值、不相交的支撑，以及最终应用韦伊互反律。我们可以证明这个额外的 ϕ 项有效地 消失，从而为我们提供双线性性。

我就像“啊，好的”……但是我不明白

所以，是的！虽然配对公式起初可能看起来很随意，但它与韦伊互反律紧密相关，而韦伊互反律是将这一切联系在一起的粘合剂！

泰特配对

这是一个配对——但我想向你展示另一个配对。

它与上一个配对有点不同——虽然韦伊配对要求两个输入都来自 r-挠点，但泰特配对稍微灵活一些，因为它形式上只需要其中一个输入是 r-挠点。

我想你现在已经很累了。

如果需要，休息一下！

不过有个坏消息：尽管有额外的灵活性，但这个配对可以说 更复杂 比上一个。我会尽量保持友好！

首先，我们需要一些定义。

一个新的群

正如我们已经知道的那样，r-挠点是所有满足 [r]P = 𝒪 的点集。

现在，当我们用 r 乘以 其他点 时会发生什么？让我们将它们全部收集到另一个集合 rE 中。

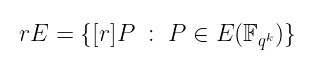
这只是所有“r 乘以某物”的点的集合。事实证明，这形成了椭圆曲线的 子群。

类似于我们处理 商环 的方式，我们可以使用这个群来定义一个“商群”E/rE——解释为“E mod rE”，其中如果两个点的 差 在 rE 中，则认为这两个点相同。

换句话说，如果对于某个点 Q，P₁ - P₂ = [r]Q，则点 P₁ 和 P₂ 是 等价的。

现在，假设我们选择某个点 P。然后我们通过以下策略开始生成点：选择另一个点 Q₁，并计算 P + [r]Q₁。然后对 Q₂、Q₃、Q₄ 等执行相同的操作，直到你用完曲线中的点。

你会发现你已经获得了 E 的 子集。如果你选择另一个起点（不在这个新子集中），你将获得一个 完全不同的子集，与前一个子集完全 不相交。

这些不相交的集合，我们称之为 陪集。它们代表 等价类。

总而言之，E/rE 是 等价类 的集合，或者是所述陪集的代表。

是的，我知道。这到底有什么意义？

泰特配对是通过从 r-挠点获取一个输入，从 E/rE 获取另一个输入来定义的。虽然，在适当的情况下，会发生一些非常神奇的事情：每个 r-挠点代表一个 唯一、不同的陪集！

这意味着——我们可以最终从 r-挠点获取两个输入。

配对

考虑到这一点，让我们继续进行定义。让我们以（准）严格的方式进行。

设 P 为 r-挠点中的一个点，我们知道我们可以找到一个除数为 (f) = r(P) - r( 𝒪 ) 的函数，设 Q 为 E/rE 的代表。此外，我们需要一个除数，使得：

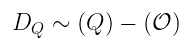
与 (f) 不相交的支持。有了这个，泰特配对只是映射：

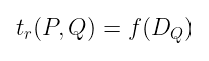
在这种情况下，此配对的输出是 等价类 的一个成员：

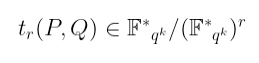
正如你现在所期望的那样定义。

这并不好——通常，在配对计算中，我们依赖于不同方能够计算 完全相同的值 的事实，而不是等价类的代表。为了避免这种情况，我们引入了 约化泰特配对 作为：

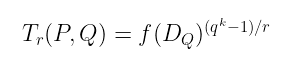
这所实现了的（让我们说是 神奇地，但你可以自己检查！）是将结果等价类中的所有元素发送到字段中 唯一的第 r 个单位根。

证明双线性性与韦伊配对的情况没有太大区别，所以我将其作为练习留给你！

总结

好了！今天就到这里。

我们今天定义了两个主要的配对，花时间研究使它们起作用的一些更微妙的细节。虽然我们定义中的不同组成部分感觉非常简单，但所有这些定义都植根于我们如果希望保持简短就根本无法在此处涵盖的深刻数学中。

诸如拓扑学、代数几何、伽罗瓦理论和复分析。

此外，你可能会发现这些配对的一些变体或优化——但是两个基本定义是我们刚刚看到的两个。

所有这些 函数定义 都非常棒，但是我们没有说关于如何有效地 计算配对 的任何内容。就像我们有用于点乘的 double-and-add 规则一样，我们将看到配对计算也需要引入一种有效的技术才能可行。

迹 和 反迹映射 在所有这些中扮演什么角色？

不要担心——这些问题将在我们下次见面时得到解答！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～