MiMC7哈希算法

MiMC 7 哈希

我们典型的密码学哈希，例如 SHA-256，通常在零知识证明（例如 zkSNARKs）中实现起来成本太高。为此，我们需要一种可以在有限域上实现的哈希方法。三种典型的方法是 Pedersen 哈希 [ 这里], Posiden 哈希 [ 这里] 和 MiMC (最小乘法复杂度) 哈希 [1][ 这里]:

MiMC 的一个重要特征是具有较低的乘法复杂度，这在多方计算 (MPC)、全同态加密 (FHE) 和 ZKP 等领域中使用。Dan Bohen 等人[2] 还提出了将其用于 VDF（可验证延迟函数），因为 MiMC 的复杂度仅为 AES 的 1.6%。

在原始论文中，存在以下映射：

F(x) = x³

但 MiMC-7 使用：

F(x) = x⁷

总的来说，我们有一个包含 q 个元素的有限域 (F_q)，并迭代 r 次的 round 函数——其中 q 是一个素数。在每一轮中，我们添加一个密钥 (k) 值和一个 round 常数 (c_i)——除了第一轮之外——以及 F(x)=x⁷ 的非线性函数：

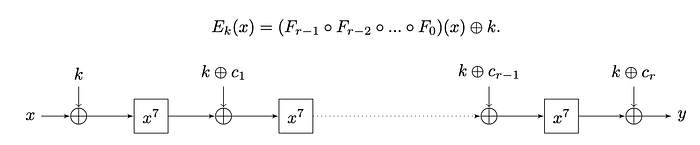
参考文献 [ 这里]

然后我们可以定义一个初始值 (xIn) 为零，一个 k 值（一个大整数向量）和 round 数量：

h1,_ := mimc7.HashGeneric(big.NewInt(0), k, rounds)

下面是单个 round 的基本实现，针对 t 的一个元素，然后在 round 结束时添加 k：

for number_of_rounds:
    t2 := ff.NewElement().Square(t)
    t4 := ff.NewElement().Square(t2)
    r = ff.NewElement().Mul(ff.NewElement().Mul(t4, t2), t)
    t = ff.NewElement().Add(ff.NewElement().Add(r, k), c_i)

rE := ff.NewElement().Add(r, k)

我们看到 r=t².t⁴.t = t⁷，其中我们让 t=r+k+c+i 用于每一轮。这里的核心优势是我们在计算中未使用乘法元素。

以下定义了 k 中三个值的代码，其中 x 的输入值为零 [ 这里]：

package main

import (
 "fmt"
 "github.com/iden3/go-iden3-crypto/v2/mimc7"
 "math/big"
 "os"

)

func main() {

 x_0:="0"
 k_0:="1"

 argCount := len(os.Args[1:])

 if argCount > 0 {x_0 = os.Args[1] }

 if argCount > 1 {k_0 = os.Args[2] }

 x,_ := new(big.Int).SetString(x_0,10)
 k,_ := new(big.Int).SetString(k_0,10)

 h1 := mimc7.MIMC7Hash(x, k)

 fmt.Printf("Input: %s\nKey: %s\n\nMimc7 Generic Hash: %s\n\n",x,k,h1)

}

一个示例运行是 [ 这里]：

Input (x): 0
Key (k): 1

Mimc7 Generic Hash: 8114461605833343697468854264706876497726540090029823113980243221325210187593

这是实现：

MiMC-7 Hash and Golang [ MiMC-7 Hash and Golang]

性能

总的来说，MiMC7 具有出色的性能，并且在编译、设置和创建证明的时间方面，与 SHA-256 相比性能提高了 100 倍以上，并且占用的内存不到十分之一 [ 这里]：

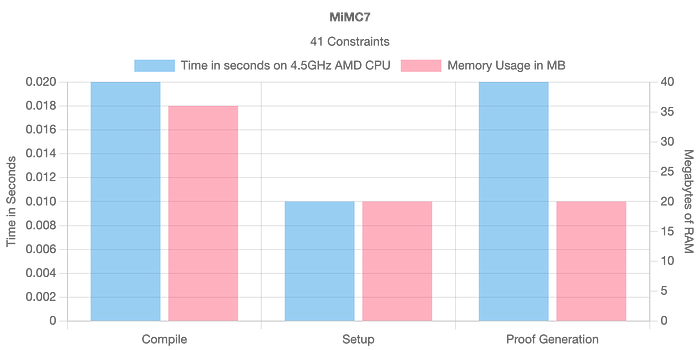
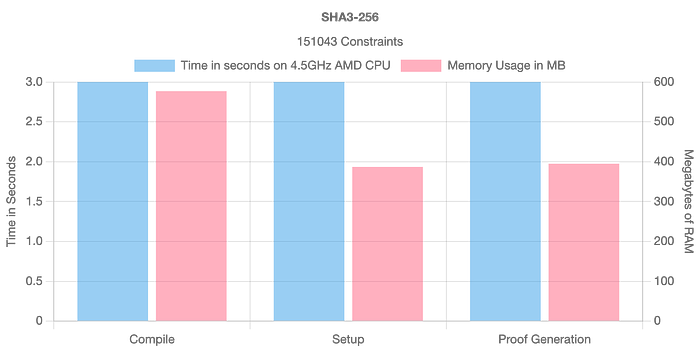
在ZK-SNARKs中，每种哈希方法的执行时间和内存消耗与所用方法的约束数量成正比。我们可以从下图中看到，SHA-256和SHA-3具有最高的开销，而Blake2s具有改进的性能。但是，我们可以看到，MiMC7通常具有所有定义的方法中最好的性能。

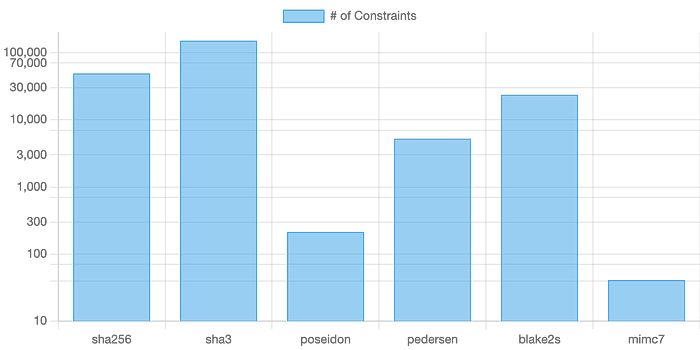
参考文献 [ 这里]

结论

对于 zk 电路，MiMC7 在降低复杂性方面是赢家，因此也提高了性能。

参考文献

[1] Albrecht, M., Grassi, L., Rechberger, C., Roy, A., & Tiessen, T. (2016, November). MiMC: Efficient encryption and cryptographic hashing with minimal multiplicative complexity. In 国际密码学理论与应用会议 (pp. 191–219). Berlin, Heidelberg: Springer Berlin Heidelberg.

[2] Boneh, D., Bonneau, J., Bünz, B., & Fisch, B. (2018, July). Verifiable delay functions. In 年度国际密码学会议 (pp. 757–788). Cham: Springer International Publishing.

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～