Circle FFT - 第一部分：构建圆形域（Circle Domain）

Circle FFT — 第一部分：构建圆形域

Circle STARKs 是一种新的 zk-STARK 方案，已经在 Stwo 和 Plonky3 中实现，并已被多个 zkVM 项目采用。它的主要创新在于能够使用小的 32 位字段（梅森素数 $2^{31}−1$），同时保持高效 FFT 运算所需的数学特性。在本系列解释性文章中，我们将讨论 Circle STARK 背后的主要算法，即 Circle FFT。

在第一部分文章中，我们首先回顾一下 STARK 友好的素数是如何演变的，然后我们探讨 Circle FFT 的基本概念——即圆形曲线、它的群结构，以及 twin-cosets 和 standard-position cosets 的作用，并提供详细的示例和推导。然后，在第二部分文章中，我们将详细描述 Circle FFT 算法本身。

我们还提供了这些核心思想的演练——例如圆形群和 Circle FFT——以及 $p=31$（指数为 5 的 梅森 Mersenne 素数：$2^5−1$ ）的显式示例计算和 Python 脚本。

我们的重点是这些构建块中的每一个如何引导到一个完整的类 FFT 例程，即使 $p−1$ 没有大的 two-adic 因子。

如果你有兴趣自己运行这些示例，完整的 Python 代码可在此处找到，我们将在后面的章节（如第 4 节和第 6 节）中引用它，在这些章节中，我们将逐步介绍代码中的群和域的构建。

本文由 Yugo 与 RareSkills 合作撰写。本文由 Soulforge Grant 资助。我们感谢他们的支持。

0. 从 STARK 友好素数到 Mersenne 31

在深入研究 STARK 友好素数之前，让我们首先回顾一下有限域的基础知识。

域是一个定义了加法、减法、乘法和除法（除以零除外）的集合。当元素集合是有限的时，它被称为有限域。$\mathbb{F}_p$ 指的是从 0 到 $p−1$（其中 p 是素数）的整数集合，其中加法、减法和乘法都以模 p 计算，除法定义为模 p 乘法的逆运算。

我们用 $\mathbb{F}_p^$ 表示集合 $\mathbb{F}_p \setminus {0}$。 $\mathbb{F}_p$ 中的每个元素都有一个乘法逆元，因此 $\mathbb{F}_p$ 可以被视为一个乘法群。这个群的大小 $|\mathbb{F}_p^|$ 是 $p−1$。当我们把 $p−1$ 分解成它的素因子时，如果一个素数 q 出现 r 次，那么就存在一个大小为 $q^r$ 的循环子群。

你可以用一个小的素数简单地说明这一点，例如 $p=7$。因为$ p−1=6 $分解为$ 2×3$，所以必须存在大小为 2 和 3 的子群。事实上，在 $\mathbb{F}_7^* = {1,2,3,4,5,6}$ 中，元素 6 生成一个大小为 2 的子群 {1,6}，而元素 2 生成一个大小为 3 的子群 {1,2,4}。

在许多 STARK 协议中，数论变换 (NTT) 或快速傅里叶变换 (FFT) 依赖于这样一个子群，其中因子是 2 的幂，因此子群的大小为 $2^r$。使得 $2^r$ 整除$ (p−1) $的最大整数 r 称为 two-adicity。高的 two-adicity 允许 FFT/NTT 域具有更大的 2 的幂大小，这对于实现快速多项式求值、插值和多项式乘法至关重要。此外，高效地实现这些基于 NTT 的操作在很大程度上取决于快速模乘法——因为 FFT/NTT 涉及重复地将元素相乘并将它们简化为模 $p$。

最初，STARK 使用素数 $p = 2^{251} + 17 \cdot 2^{192} + 1$，它的 two-adicity 为 $192$。在现代 STARK 实现中，其中一个改进是通过减小有限域的大小来降低开销。例如，Goldilocks 域是 $p=2^{64}–2^{32}+1$，它的 two-adicity 为 32。至关重要的是，因为 $2^{64}≡2^{32}–1(mod \ p)$，两个 64 位数的乘积可以在基 $2^{32}$ 中分割，并且只需几次加法和减法就可以进行约简。

那么 Circle STARKs 呢？正如 Circle STARKs paper 中提出的，它使用梅森素数，

$p=2^{31}–1$。

梅森素数是对于某个整数 n，形如 $2^n−1$ 的素数。这里，n=31 得到 $2^{31}−1$，它恰好是素数，因此被归类为梅森素数。

选择 $2^{31}−1$ 的一个主要原因是它适合 32 位机器字，使得模乘法非常快。具体来说，当两个 32 位数字相乘时，结果是一个 64 位的值，并且模 $2^{31}−1$ 的约简只需要两次加法就可以完成。

使用向量化指令，此操作可以更快。现代 CPU 擅长本地处理 32 位整数，梅森 31 ($2^{31}−1$) 符合此架构，从而可以最佳地利用硬件功能。与原始 STARK 中使用的 256 位素数相比，正如 Eli Ben-Sasson 在 Why I’m Excited By Circle Stark And Stwo 中讨论的那样，梅森 31 提供的模乘法速度快大约 125 倍，并且比 Baby Bear ($2^{31}–2^{27}+1$) 快 1.3 倍。

然而，传统的 FFT 或 NTT 方法需要在 p−1 中有一个大的 2-adic 因子，以便在 $\mathbb{F}_p^$ 中形成足够大的 2 的幂子群。这里，$|\mathbb{F}_p^| = p – 1 \;=\; 2^{31} – 2$，它的 two-adicity 只有 1。因此，我们不能直接使用乘法下的大的 2 的幂子群。

Circle STARK 仍然使用梅森素数域$ p=2^{31}–1$。然而，不是直接使用 Fp 本身，我们观察到曲线 $$ x^2+y^2=1 $$ 在 $\mathbb{F}_p$ 上（其中 pequiv3pmod4）恰好有 p+1 个点。例如，当 $p=3;(=2^2–1)$ 时，恰好有四个这样的点：(0,1),(0,2),(1,0),(2,0)。

这至关重要，因为 p+1 可以包括 2 的大幂，从而创建大小为 $2^n$ 的子群。因此，Circle STARK 不是使用 $\mathbb{F}_p$ 中的单个元素，而是考虑满足$ x^2+y^2=1$ 的 pairs$ (x,y)∈\mathbb{F}_p^2$ （即圆形曲线上的点）。通过这样做，Circle STARK 可以实现自己的快速多项式插值和求值——通常被称为 Circle FFT——直接在这些圆形元素上进行。

1. 圆形曲线

让我们继续讨论 Circle STARKs 的核心数学。有限域 Fp 上的圆形曲线是由满足以下条件的所有点 (x,y) 组成的 Fp2 的子集

$$ x^2+y^2=1 $$

我们有时用 C(Fp) 来表示这个集合，或者简称为“圆形”。

在 Circle STARKs 中，我们关注 p≡3(mod4) 的素数 p（例如，p=3,7,11,…）。在这种条件下，−1 不是 Fp 中的平方。具体来说，这确保了方程 x2+y2=1 在 Fp2 中恰好有 p+1 个解，而没有额外的异常值解（即，无穷远处的点）。对于本文，我们只需要在这种情况下的 x2+y2=1 在 Fp2 中恰好产生 p+1 个点。

（然而，对于那些对几何视角感兴趣的读者，想了解为什么 p≡3(mod4) 会导致恰好 p+1 个解，请参阅附录。）

1.1 玩具示例 p=7≡3(mod4)

例如，如果 p=7（即 3(mod4)），那么 C(F7) 是所有 (x,y)∈F72 的集合，使得 x2+y2=1。

https://pub-32882f615aa84e4a94e1279ccf3ab85a.r2.dev/CircleStarks/circleF7.MP4

以下是 F72 中满足 x2+y2≡1(mod7) 的一些对 (x,y) 。例如：

• (1,0) 和 (0,1) 很明显，因为 12+02=1 且 02+12=1。
• (5,2) 也可以，因为 52+22=25+4=29，且 29mod7=1。

我们看到对于 p=7，恰好有 8 (p+1) 个这样的对。

2. 圆形群

这种集合用 C(Fp) 表示，通常被称为在 Fp 上的圆形曲线。一个引人注目的事实是 |C(Fp)|=p+1。例如，如果 p=7，那么圆形上恰好有 7+1=8 个点——值得注意的是 8=23。

这很重要，因为在通常的 STARK 设置中，我们通常需要大小为 2n 的域用于类 FFT 操作。在 p=7 的情况下，圆形上恰好有 8 个点意味着我们可以形成大小为 2n 的子群。稍后，我们将看到这种属性（p+1 中的高 2-adicity）是如何在 Circle FFT 中被利用的。

一个关键属性是 C(Fp) 可以通过对其点进行群操作（本质上是一个二元运算符）来给出。具体来说，我们使用“⋅”来表示这个操作：对于 C(Fp) 中的两个点 (x0,y0) 和 (x1,y1)，

(x0,y0)⋅(x1,y1)=(x0x1–y0y1,x0y1+y0x1).

我们可以检查这个群操作是否仍然在 C(Fp) 中（结果仍然满足 x2+y2=1），并使该集合成为大小为 p+1 的循环群。

2.1 检查群公理

作为群的公理，我们通常列出以下四个属性：封闭性、单位元、逆元和结合律。让我们仔细看看每一个，以确认它们都成立。

2.1.1 封闭性

在圆形上取两个点 (x0,y0) 和 (x1,y1)；

x02+y02=1 和 x12+y12=1。

定义一个新点

(x^,y^)=(x0x1−y0y1,x0y1+y0x1)。

我们将通过逐步计算 (x^2+y^2) 来证明 (x^,y^) 也位于圆形上：

x^2+y^2=(x0x1–y0y1)2+(x0y1+y0x1)2// 展开平方=x02x12−2x0x1y0y1+y02y12+x02y12+2x0y1y0x1+y02x12=x02x12+y02y12+x02y12+y02x12// canceled ±2x0y1y0x1=x02(x12+y12)+y02(x12+y12)// factor out (x12+y12)=(x02+y02)(x12+y12)// 再次分解 using x02+y02

因为我们知道 x02+y02=1 和 x12+y12=1，我们将这些值代入乘积：

x^2+y^2=(x02+y02)(x12+y12)=1×1=1.

因此 (x^,y^) 也满足 (x^2+y^2=1)，因此位于圆形上。这证实了集合在运算下是封闭的

(x0,y0)⋅(x1,y1)=(x^,y^).

2.1.2 单位元

点 (1,0) 充当群操作下的单位元。具体来说，对于圆形上的任何 (x,y)，

(1,0)⋅(x,y)=(1⋅x–0⋅y,1⋅y+0⋅x)=(x,y),

人们可能想知道点 (0,1)。如果我们尝试使用 (0,1) 作为单位元，我们发现它失败了：

(0,1)⋅(x,y)=(0⋅x–1⋅y,0⋅y+1⋅x)=(−y,x),

对于一般的 x,y，它不等于 (x,y)。因为单位元是唯一的，(0,1) 不能是单位元。

2.1.3 逆元

在一个群中，元素 (x,y) 的逆元是满足以下条件的唯一点 (x′,y′)

(x,y)⋅(x′,y′)=(1,0).

在圆形上，我们看到 (x,−y) 用作 (x,y) 关于群操作的逆元。事实上，

(x,y)⋅(x,−y)=(xx–y(−y),x(−y)+yx)=(x2+y2,0)=(1,0),

因为 x2+y2=1。因此，关于群运算 (x,y) 的逆元是 (x,−y)。

2.1.4 结合律

最后一个群公理是结合律：对于任何三个点

(x0,y0),(x1,y1),(x2,y2) 在圆形上，

((x0,y0)⋅(x1,y1))⋅(x2,y2)=(x0,y0)⋅((x1,y1)⋅(x2,y2)).

这可以通过展开多项式来验证，但我们不会在此处详细介绍，因为它太长了。

2.2 一个特殊的操作：平方映射 π

除了这些群公理之外，圆形上还有另一个操作在后面的章节中特别有用，尤其是在 Circle FFT 中，即平方映射。此映射将群操作应用于点本身：

π(x,y)=(x,y)⋅(x,y)=(x2–y2,2xy).

由于圆形满足 x2+y2=1，我们得到 x2–y2=2x2–1，所以

π(x,y)=(2x2–1,2xy).

在 Circle FFT 中，我们将使用 π 以递归方式将某些求值域减半——每次应用 π 都会将域大小减少 2 倍。这是因为 π 与群操作兼容。具体来说，对于圆形上的两个点 P 和 Q，

π(P⋅Q)=π(P)⋅π(Q).

这种兼容性意味着 π 将大小为 2n 的 twin-coset 映射到大小为 2n−1 的另一个 twin-coset。我们稍后将详细讨论此域减半属性。

2.3 一种特殊的操作：对合 J

除了平方映射之外，还有另一个重要的操作。此操作称为对合，定义为

J(x,y)=(x,−y).

从几何上讲，它翻转 y 坐标的符号，同时保持 x 坐标不变。请注意，J 是它自己的逆——应用 J 两次会返回到原始点：

J(J(x,y))=J(x,−y)=(x,y).

在圆形 x2+y2=1 上，对合 J(x,y) 保持曲线上的每个点（因为对 y 取反不会影响 x2+y2）。但是，y=0 的点在 J 下是固定的，这意味着 J(x,0)=(x,0)。

2.4 p=31 处圆形群的具体运算

在之前的具体示例中，我们探讨了 p=7 的 C(Fp)，它作为构建直觉的有用玩具示例。但是，p=7 太小，无法揭示圆形群更深层次的结构属性——例如更长的子群链或 twin-cosets 或 standard positon coset 的构造。

因此，我们现在转向一个稍微大一点的素数 p=31（满足 p=25–1），以更有效的方式说明这些更丰富的行为。

给定 p=31，它与 3(mod4) 一致，集合点 (x,y)∈F312 满足方程 x2+y2=1，表示为 C(F31)，如下图所示：

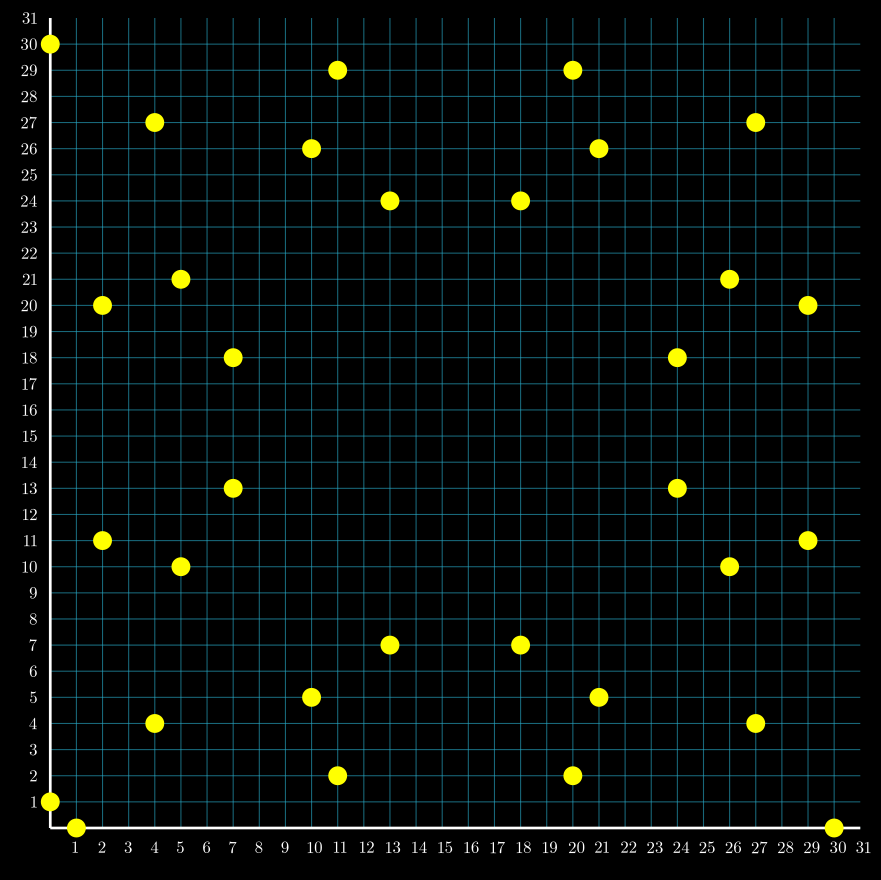
以下是 F312 中满足 x2+y2≡1(mod31) 的几个对示例 (x,y) ：

• (5,10) 也可以，因为 52+102=25+100=125，且 125mod31=125–4⋅31=1。
• (7,13) 也是一个解：72=49≡18 (mod 31) 且 132=169≡14 (mod 31)，所以 18+14=32≡1 (mod 31)。
• (30,0) 表明 30≡−1(mod31)， 因此 (−1)2+02≡1 (mod 31)。

要查看圆形群，让我们在 F31 上进行运算，其中圆形 C(F31) 有 32 个点。假设我们选择点

Q=(13,7).

我们可以通过群操作将 Q 与点 (30,0) 组合：

(13,7)⋅(30,0)=(13⋅30–7⋅0,13⋅0+7⋅30)=(390,210)≡(18,24)(mod31).

事实上，可以验证

182+242≡324+576≡900≡1(mod31),

因此 (18,24) 也位于圆形 x2+y2=1 上。同时，Q 的逆是

Q−1=(13,−7)≡(13,24)(mod31),

因为

(13,7)⋅(13,24)=(1,0).

此外，平方映射可以作用于点 Q=(13,7)。回想一下

π(x,y)=(x,y)⋅(x,y).

因此，

π(Q)=(13,7)⋅(13,7)=(13⋅13–7⋅7,13⋅7+7⋅13)≡(27,27)(mod31).

3. 圆形群的子群

我们已经确定 C(Fp) 是大小为 p+1 的循环群。如果 p+1 是 2 的幂，假设 p+1=2m，那么存在一个嵌套的子群链 G0⊂G1⊂G2⊂…⊂Gm=C(Fp)，其中每个 Gk 都有阶 |Gk|=2k。换句话说，G1 是大小为 2 的子群，G2 是大小为 4 的子群，依此类推，直到 Gm=C(mathbbFp) 本身，其大小为 2m=p+1。

例如，如果 p=31（所以 p+1=32=25），我们得到一个链 G0,G1,G2,G3,G4,G5，其中 $G 5 = C(mathbb{F}{31}) 并且每个G_k的大小为2^k$。摘要可能如下所示：

k		Gk	=2k
G0	1
G1	2
G2	4
G3	8
G4	16
G5	32

下面，我们明确地列出了 C(F31) 中的每个子群。

Size 1:  [Point(1, 0)]
Size 2:  [Point(1, 0), Point(30, 0)]
Size 4:  [Point(1, 0), Point(0, 30), Point(30, 0), Point(0, 1)]
Size 8:  [Point(1, 0), Point(4, 27), Point(0, 30), Point(27, 27), Point(30, 0), Point(27, 4), Point(0, 1), Point(4, 4)]
Size 16:  [Point(1, 0), Point(7, 13), Point(4, 27), Point(18, 24), Point(0, 30), Point(13, 24), Point(27, 27), Point(24, 13), Point(30, 0), Point(24, 18), Point(27, 4), Point(13, 7), Point(0, 1), Point(18, 7), Point(4, 4), Point(7, 18)]
Size 32:  [Point(1, 0), Point(2, 11), Point(7, 13), Point(26, 10), Point(4, 27), Point(21, 5), Point(18, 24), Point(20, 29), Point(0, 30), Point(11, 29), Point(13, 24), Point(10, 5), Point(27, 27), Point(5, 10), Point(24, 13), Point(29, 11), Point(30, 0), Point(29, 20), Point(24, 18), Point(5, 21), Point(27, 4), Point(10, 26), Point(13, 7), Point(11, 2), Point(0, 1), Point(20, 2), Point(18, 7), Point(21, 26), Point(4, 4), Point(26, 21), Point(7, 18), Point(2, 20)]

4. Python 代码 1：圆形群

我们现在将通过简单的 Python 实现来回顾圆形群代码。这里仅描述了最重要的函数或部分，所有代码都可在此处获得 here。

在这里，我们定义了两个关键类 - FieldElement 和 CirclePoint - 分别处理底层有限域中的算术和曲线上的群操作。

4.1 FieldElement

首先，FieldElement 类定义了有限域 F31 中的算术运算，例如模 31 的加法、乘法和求逆。这是圆形曲线上的所有计算的基础。

## Mersenne 5
MOD = 31

class FieldElement:
    def __init__(self, value):
        """Initialize a field element"""
        self.value = value % MOD

    def __add__(self, other):
        """Add two field elements"""
        return FieldElement((self.value + other.value) % MOD)

    def __mul__(self, other):
        """Multiply two field elements"""
        return FieldElement((self.value * other.value) % MOD)

    def inv(self):
        """Compute the multiplicative inverse"""
        return FieldElement(pow(self.value, MOD - 2, MOD))

    def square(self):
        """Compute the square"""
        return self * self

4.2 CirclePoint

CirclePoint 类表示圆形曲线 x2+y2=1 上的点。add 方法实现群操作，而 double 应用平方映射。

class CirclePoint:
    def __init__(self, x, y):
        """Initialize a point on the circle x^2 + y^2 = 1"""
        if (x.square() + y.square()).value != 1:
            raise ValueError("Point does not lie on the circle")
        self.x = x
        self.y = y

    def add(self, other):
       """Perform group operation: (x1,y1)・(x2,y2) = (x1*x2 - y1*y2, x1*y2 + x2*y1)."""
        nx = self.x * other.x - self.y * other.y
        ny = self.x * other.y + other.x * self.y
        return CirclePoint(nx, ny)

    def double(self):
        """Apply squaring map: π(x,y) = (2*x^2 - 1, 2*x*y), since x^2 + y^2 = 1."""
        xx = self.x.square().double() - FieldElement.one()
        yy = self.x.double() * self.y
        return CirclePoint(xx, yy)

    @classmethod
    def identity(cls):
        """Return the identity element (1, 0) of the circle group."""
        return cls(FieldElement.one(), FieldElement.zero())

然后，你可以模拟圆形群操作示例，如第 2.4 节所述。

例如，添加 CirclePoint (13,7) 和 CirclePoint (30,0) 会得到 Point (18,24)。

p1 = CirclePoint(FieldElement(13), FieldElement(7))
p2 = CirclePoint(FieldElement(30), FieldElement(0))

## group operation
p3 = p1.add(p2)
print(f"p1・p2 = {p3}")

p1・p2 = Point(18, 24)

将 p1=(13,7) 加倍会得到 (27,27)

## squaring map
p1_double = p1.double()
print(f"π(p1) = {p1_double}")

π(p1) = Point(27, 27)

(13,7) 的逆是 (13,24)，将它们相加会得到单位元 (1,0)

## Inverse
p1_inv = p1.inverse()
print(f"p1's inverse = {p1_inv}")
p1_plus_inv = p1.add(p1_inv)
print(f"p1・p1_inv = {p1_plus_inv}")

p1's inverse = Point(13, 24)
p1・p1_inv = Point(1, 0)

4.3 圆形群

函数 generate_subgroup 生成一个阶为 2k 的子群 Gk。它从 get_nth_generator 函数中获取适当的生成器，并重复群操作 add 以构造子群。

def generate_subgroup(k: int) -> list[CirclePoint]:
    """Generate a subgroup of size 2^k using the generator."""
    g_k = get_nth_generator(k)
    p = CirclePoint.identity()
    return [ (p := p.add(g_k)) if i else p
             for i in range(1 << k) ]

例如，你可以获得大小为 8 的子群。

G3 = generate_subgroup(3)

Size 8:  [Point(1, 0), Point(4, 27), Point(0, 30), Point(27, 27), Point(30, 0), Point(27, 4), Point(0, 1), Point(4, 4)]

5. 陪集、twin-cosets 和标准位置陪集

Twin-Cosets 和标准位置陪集是 Circle STARKs 中的域。在理解 twin-cosets 和标准位置陪集的数学属性之前，让我们简要回顾一下域在传统 STARKS 中是如何使用的。正如在第 0 节中讨论的，传统 STARKS 通常利用表示为 Fp∗ 的乘法（子）群作为它们的域。这些域有两个主要用途。

首先，当通过 IFFT 从计算跟踪构造多项式时，它们充当求值域，并且我们必须通过 FFT 使用扩展域来进行低度扩展（LDE），并且我们还必须构造约束多项式并在 LDE 上求值它们。

其次，在低度测试中，特别是对于 FRI 承诺，必须通过 FFT 在递归 FRI 折叠步骤中迭代减半的域上对多项式进行求值。

此外，在 FRI 折叠步骤中，随着多项式的度数减半，域的大小也需要减半。减半域大小对于 FRI 和 FFT 都至关重要。当我们继续时，请记住这一点。

因为虽然圆形群本身已经提供了高的 two-adicity，但 Twin-Cosets 或标准位置陪集的构造确保在 FFT 中的递归平方步骤期间，求值域（即 Twin-Cosets 或标准位置陪集）也可以减半其大小，同时保持其陪集结构。这对于在每个递归级别中在这些域上启用类 FFT 操作至关重要。

5.1 陪集

让我们回顾一下群论中陪集的定义。假设 H 是群 G 的子群，并假设 Q∈G。那么 Q 对 H 的左陪集是集合

Q⋅H={Q⋅h∣h∈H}.

如果 Q∈H，那么 Q⋅H=H。否则，在 Q∉H 的情况下，Q⋅H 是与 H 不相交的集合，但仍然具有与 H 相同的大小。这是因为如果 Q∈H，则 H 在群运算下的封闭性确保 Q⋅H=H，而如果 Q∉H，则 Q⋅H 的任何元素都不能在 H 中，而不暗示 Q∈H，并且双射 h↦Q⋅h 保留了大小。

在我们的特定设置中，G=C(Fp)，它是大小为 p+1 的循环群。从上一节中，我们知道存在一个子群链 G0⊂G1⊂⋯⊂Gm，其中 |Gk|=2k。

因此，例如，如果我们固定一个阶为 2n−1 的 Gn−1，那么对于圆形上的任何点 Q，陪集

Q⋅Gn−1={Q⋅g∣g∈Gn−1}

被称为 Gn−1 的陪集。该集合将具有相同的基数 2n−1，并且与 Gn−1 本身是不相交的，除非 Q 已经属于 Gn−1。

5.1.1 陪集示例

让我们快速说明这个例子。在 p=31 的情况下，回想一下 p+1=32=25，因此存在一个子群链 G1,G2,…,G5，其中 |G1|=2。具体来说，

G1={(1,0),(30,0)}.

现在取一个不在 G1 中的点 Q。例如，

Q=(2,11).

由于 Q 不在 G1 中，集合

Q⋅G1={(2,11)⋅(1,0),(2,11)⋅(30,0)}

将是 G1 的一个不同的陪集，与 G1 本身不相交。

• (2,11)⋅(1,0)=(2⋅1–11⋅0,2⋅0+11⋅1)=(2,11),

• (2,11)⋅(30,0)=(2⋅30–11⋅0,2⋅0+30⋅11)≡(29,20)(mod31).

因此，

Q⋅G1={(2,11),(29,20)},

它确实具有大小 2。这是对应于 Q=(2,11) 的 G1 的陪集，显然不同于子群 G1 本身。

5.2 Twin-Cosets

我们现在通过取两个陪集的并集来定义 twin-coset：Q⋅Gn−1 和其逆陪集 Q−1⋅Gn−1。具体来说，令

D=(Q⋅Gn−1)∪(Q−1⋅Gn−1).

如果满足以下条件，我们说 D 是大小为 2n 的 twin-coset：

1. 不相交性 两个陪集 Q⋅Gn−1 和 Q−1⋅Gn−1 是不相交的。 在实践中，这种不相交性等同于确保 Q2∉Gn−1。这个等价性来自陪集的性质。如果 Q2∈Gn−1，那么 Q=Q−1⋅Q2 既在 Q⋅Gn−1 中又在 Q−1⋅Gn−1 中（重叠）。相反，如果陪集不重叠，那么 Q 不能写成 Q−1⋅g（对于任何 g∈Gn−1），这意味着 Q2∉Gn−1。

2. 在对合 J 下没有不动点 如果 f(P)=P，则点 P 被称为映射 f 的不动点。在我们的例子中，我们考虑对合 J(x,y)=(x,−y)。如果 D 包含任何 y=0 的点，那么 J(x,0)=(x,0) 将保持不变。它是一个不动点。我们想避免在 D 中有这样的点，因为根据定义，twin-coset 排除了 J 的任何不动点。

在这些条件下，每个陪集 Q⋅Gn−1 和 Q−1⋅Gn−1 有 2n−1 个不同的点，总共在 D 中有 2n 个点。直观地，我们将一个陪集与其逆陪集合并，形成一个 2n 个元素的域。

5.2.1 Twin-Coset 示例

从第 5.1.1 节中的陪集示例继续（我们在其中选择了不在 G1 中的 Q=(2,11)），让我们现在形成一个大小为 2n=22=4 的 twin-coset。我们已经看到了：

Q⋅G1={(2,11),(29,20)}.

接下来，计算 Q−1=(2,20) 并形成陪集 Q−1⋅G1：

Q−1⋅G1={(2,20)⋅(1,0),(2,20)⋅(30,0)}

• (2,20)⋅(1,0)=(2⋅1−20⋅0,2⋅0+D=Q⋅Gn−1∪Q−1⋅Gn−1=Q⋅Gn.

这里，回想一下，Gn 是 C(Fp) 中阶数为 2n 的唯一子群，如第 3 节前面介绍的那样。我们有一个子群链：

G0⊂G1⊂⋯⊂Gn⊂⋯⊂C(Fp),

并且每个 Gk 的大小为 2k。因此，Gn 包含 Gn−1，我们将使用一个阶数为 2n+1 的点 Q 来关联这些子群的陪集。

让我们逐步拆解这个过程：

首先，由于 Gn−1⊂Gn，我们可以将 Gn 视为由 Gn−1 的两个不相交的陪集组成，即：

Gn=Gn−1∪R⋅Gn−1, 对于某个 R∉Gn−1。

如果我们将它乘以一个阶数为 2n+1 的固定点 Q，我们得到：

Q⋅Gn=Q⋅Gn−1∪Q⋅R⋅Gn−1.

结果证明 Q⋅R=Q−1，所以：

Q⋅Gn=Q⋅Gn−1∪Q−1⋅Gn−1.

因此，陪集 Q⋅Gn 可以写成两个不相交的陪集的并集：一个由 Q 产生，另一个由 Q−1 产生，每个都作用于较小的子群 Gn−1 之上。这正是 twin-coset 的定义。

但并非所有 twin-coset 都是以这种方式产生的。为了确保这个构造正常工作，我们需要：

1. 不相交性：Q2∉Gn−1。否则，这两个陪集会重叠。
2. 对合下没有不动点：结果集 D 必须避免 y=0 的点，因此对合 J(x,y)=(x,−y) 在 D 中没有不动点。
3. 正确的阶：Q 必须具有阶 2n+1，以保证 Q⋅Gn 恰好跨越 2n 个不同的元素。

当这些条件满足时，陪集 D=Q⋅Gn 给出一个标准位置陪集：一个大小为 2n 的域，它同时是一个 twin-coset 和一个较大子群的单个陪集。

5.4 手动计算示例：p=31 时的 Twin-Coset 和标准位置陪集

下面，我们演示了当 p=31 时，twin-coset 和标准位置陪集的概念如何应用。我们有 p+1=32=25，因此存在子群 G1,G2,G3,G4,G5，其中 |G3|=8 且 |G2|=4。我们将展示 G3 的标准位置陪集，即 D=Q⋅G2∪Q−1⋅G2=Q⋅G3。

5.4.1 Twin-Coset 构造

• 设置 令 n=3。那么 G2 的大小为 4。选择一个阶数为 16 的点 Q（因此 Q∉G3，但 Q∈G4）。具体来说，可以选择 Q=(13,7)

• 形成 Twin-Coset

D=(Q⋅G2)∪(Q−1⋅G2).

由于 G2 具有四个点 (1,0)、(0,30)、(30,0) 和 (0,1)，因此每个点都乘以 Q=(13,7) 或 Q−1=(13,24)。

1. Q⋅(1,0)=(13,7),
2. Q⋅(0,30)=(7,18),
3. Q⋅(30,0)=(18,24),
4. Q⋅(0,1)=(24,13),
5. Q−1⋅(1,0)=(13,24),
6. Q−1⋅(0,30)=(24,18),
7. Q−1⋅(30,0)=(18,7),
8. Q−1⋅(0,1)=(7,13).

D=(Q⋅G2)∪(Q−1⋅G2)={(13,7),(7,18),(18,24),(24,13),(13,24),(24,18),(18,7),(7,13)}

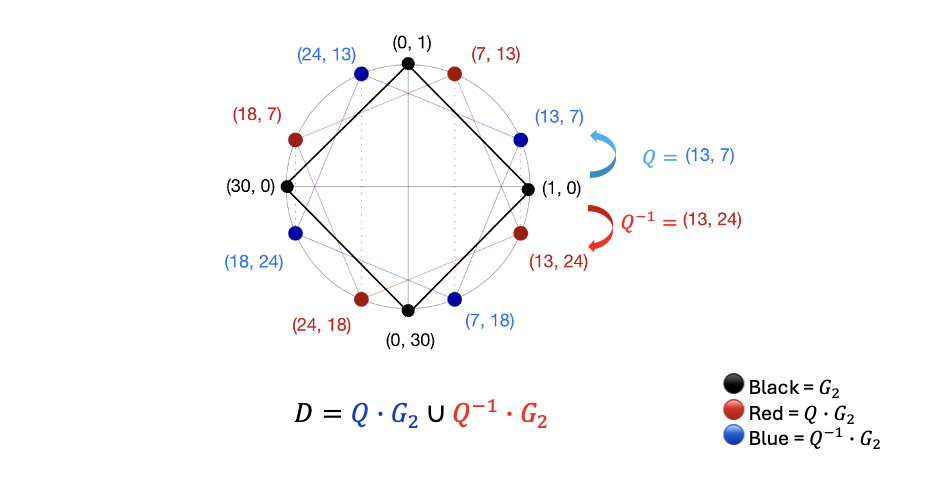
将这些组合起来得到 8 个不同的点。D 中没有元素被 J 固定，因此 D 是大小为 23=8 的 twin-coset。将这些组合起来得到 8 个不同的点。D 中没有元素被 J 固定，因此 D 是大小为 23=8 的 twin-coset。

在下图中，🔴 红色点表示 Q⋅G2，🔵 蓝色点表示 Q−1⋅G2。它们共同构成了 8 点的 twin-coset D。

5.4.2 检查标准位置陪集

这个相同的 D 也等于 Q⋅G3，对于某个大小为 8 的子群 G3 而言，这意味着 D 是一个标准位置陪集。

G3 是子群 {(1,0),(4,27),(0,30),(27,27),(30,0),(27,4),(0,1),(4,4)}，然后将每个元素乘以 Q=(13,7) 得到 D 中的 8 个点。

1. Q⋅(1,0)=(13,7)
2. Q⋅(4,27)=(18,7)
3. Q⋅(0,30)=(7,18)
4. Q⋅(27,27)=(7,13)
5. Q⋅(30,0)=(18,24)
6. Q⋅(27,4)=(13,24)
7. Q⋅(0,1)=(24,13)
8. Q⋅(4,4)=(24,18)

Q⋅G3={(13,7),(18,7),(7,18),(7,13),(18,24),(13,24),(24,13),(24,18)}.

因此

D=Q⋅G3=Q⋅G2∪Q−1⋅G2.

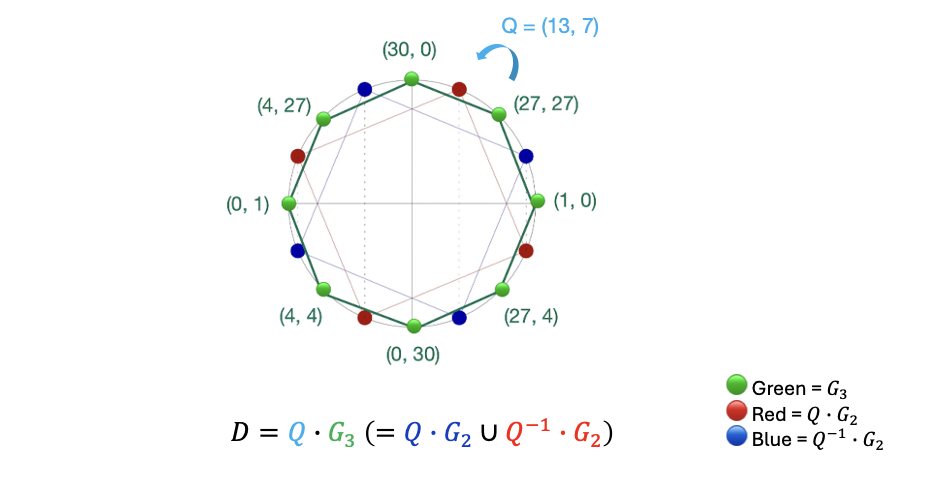
因为 D 既是 G2 的 twin-coset，又是 G3 的单个陪集，我们称它为大小为 8 的标准位置陪集。

在下图中，🟢 绿色点表示子群 G3，🔴 红色和 🔵 蓝色点分别表示两个不相交的陪集 Q⋅G2 和 Q−1⋅G2。它们的并集构成了 twin-coset D，整个 8 点集构成了标准位置陪集 Q⋅G3。

因此，每当 Q 的阶数为 2n+1 时，我们就可以构建一个大小为 2n 的标准位置陪集。这种结构在 Circle STARK 中非常重要，因为即使 p−1 的 2-adic 性不足，它也能提供一个简洁的 2n 个点的域。

6. Python 代码 2：Circle Domain

我们现在将通过 Simple Python 实现来回顾 Circle Domain 代码。域构造（例如 twin-coset 和标准位置陪集）也在同一个 Python notebook 中实现。你可以运行并检查这些集合是如何逐步构建的。

6.1 Twin-Coset

此函数通过将群运算 add 应用于 Q 及其在子群上的逆 Q−1 来生成域，确保对称性和大小为 2n。

def generate_twin_coset(Q, G_n_minus_1):
    """生成 twin-coset：D = Q・G_(n-1) ∪ Q^{-1}・G_(n-1)。"""
    Q_inv = Q.inverse()
    coset_Q = [Q.add(g) for g in G_n_minus_1]
    coset_Q_inv = [Q_inv.add(g) for g in G_n_minus_1]
    return coset_Q + coset_Q_inv

G2 = generate_subgroup(2)
Q = CirclePoint(FieldElement(13), FieldElement(7))
twin_cosets = generate_twin_coset(Q, G2)
print(twin_cosets)

[Point(13, 7), Point(7, 18), Point(18, 24), Point(24, 13), Point(13, 24), Point(24, 18), Point(18, 7), Point(7, 13)]

6.2 标准位置陪集

此函数通过将群运算 add 应用于 Q 和子群来生成标准位置陪集。

def generate_standard_position_coset(Q, G_n):
    """生成标准位置陪集 D = Q・G_n。"""
    return [Q.add(g) for g in G_n]

G3 = generate_subgroup(3)
Q = CirclePoint(FieldElement(13), FieldElement(7))
D = generate_standard_position_coset(Q, G3)

[Point(13, 7), Point(18, 7), Point(7, 18), Point(7, 13), Point(18, 24), Point(13, 24), Point(24, 13), Point(24, 18)]

这种代码，你可以检查标准位置陪集 D=Q⋅Gn−1∪Q−1⋅Gn−1=Q⋅Gn 的相等性。

D_std = generate_standard_position_coset(Q, G3)
D_twin = generate_twin_coset(Q, G2)
print("Q・G3:", D_std)
print("(Q・G2) ∪ (Q^-1・G2):", D_twin)
if set(D_std) == set(D_twin):
    print("Equal: standard position coset Q·G3 = Q·G2 ∪ Q^-1·G2")
else:
    print("Not Equal")

7. 将较大的标准位置陪集分解为较小的 Twin-Coset

在 Circle FFT 和 FRI 的许多步骤中，我们需要管理不同大小的评估域，所有这些域都位于圆曲线上。实现这一目标的一个关键方法是 Circle STARKs 论文 中的引理 2，它确保大小为 2m 的标准位置陪集可以分解为大小为 2n 的较小 twin-coset，对于任何 n≤m。

7.1 引理 2 的陈述

设 D⊂C(Fp) 为大小为 2m 的标准位置陪集。那么对于任何 n≤m，可以将 D 分解为大小为 2n 的 twin-coset。具体来说，如果

D=Q⋅Gm，其中 |Gm|=2m,

那么

D=⋃k=0(2m2n)−1(Q4k+1⋅Gn−1∪Q−(4k+1)⋅Gn−1)

简而言之，如果 D 是大小为 2m 的标准位置陪集，我们可以使用 Q 的幂将其切片成更小的 twin-coset（每个大小为 2n）。这种划分使我们可以精确地制作 Circle FFT 协议的给定步骤中所需的部分 D。

7.2 手动计算示例：将大小为 8 的标准位置陪集拆分为 2 个大小为 4 的 Twin-Coset

假设 p=31，因此 p+1=32=25。我们有子群 G1,G2,G3,…，其中 |G3|=8。

• 我们的标准位置陪集 设 D=Q⋅G3，其中 |D|=8。这里，Q 的阶数为 16，这意味着 Q∉G3 但 Q⋅G3 形成一个大小为 8 的陪集。

D=(Q⋅G2)∪(Q−1⋅G2)=Q⋅G3={(13,7),(7,18),(18,24),(24,13),(13,24),(24,18),(18,7),(7,13)}

• 目标 将 D 分解为大小为 2n=4 的 twin-coset。令 n=2，所以 |G2|=4 且 |G1|=2。 那么引理 2 表明 D=⋃k=0(8/4)−1(Q4k+1⋅G1∪Q−(4k+1)⋅G1)。

因为 8/4=2，所以我们有 k=0 和 k=1。

7.2.1 情况 k=0

• Q4⋅0+1=Q1=Q。
• G1={(1,0),(30,0)}.

计算：

1. Q⋅(1,0)=(13,7)
2. Q⋅(30,0)=(18,24)
3. Q−1⋅(1,0)=(13,24)
4. Q−1⋅(30,0)=(18,7)

因此，第一个 twin-coset 有 4 个不同的点。

7.2.2 情况 k=1

• Q4⋅1+1=Q5。 即 Q5=(24,13)。
• 同样，Q−5=(24,−13)≡(24,18)。

再次，将每个点乘以 (1,0) 和 (30,0)：

1. Q5⋅(1,0)=(24,13)
2. Q5⋅(30,0)=(7,18)
3. Q−5⋅(1,0)=(24,18)
4. Q−5⋅(30,0)=(7,13)

这产生另外 4 个点，形成第二个大小为 4 的 twin-coset。

7.2.3 两个 Twin-Coset 的并集

取两个 4 点集的并集（对于 k=0 和 k=1）恢复整个 8 元素陪集 D。因此：

D=(Q1⋅G1∪Q−1⋅G1)∪(Q5⋅G1∪Q−5⋅G1).

这完全符合引理 2 的陈述，表明如何将 8 点标准位置陪集分解为两个大小为 4 的 twin-coset。

7.3 手动计算示例：将大小为 8 的标准位置陪集拆分为 4 个大小为 2 的 Twin-Coset

我们还可以将这个大小为 8 的标准位置陪集划分为多个较小的 twin-coset。

令 n=1，所以 |G1|=2。引理 2 给出：

D=⋃k=0(8/2)−1(Q4k+1⋅G0∪Q−(4k+1)⋅G0).

由于 G0={(1,0)}，每个 twin-coset 有 2 个点：

• k=0: {Q1⋅G0=Q,Q−1⋅G0=Q−1} ={(13,7),(13,24)}
• k=1: {Q5⋅G0=Q5,Q−5⋅G0=Q−5}={(24,13),(24,18)}
• k=2: {Q9⋅G0=Q9,Q−9⋅G0=Q−9}={(18,24),(18,7)}
• k=3: {Q13⋅G0=Q13,Q−13⋅G0=Q−13}={(7,18),(7,13)}

D={(13,7),(13,24)}∪{(24,13),(24,18)}∪{(18,24),(18,7)}∪{(7,18),(7,13)}

这会将 D 分解为四个大小为 2 的 twin-coset。

8. 平方映射将 Twin-Coset 减半

虽然引理 2 侧重于将大型陪集拆分为较小的 twin-coset，但引理 3 利用平方映射将 twin-coset 的大小减半。此过程用于 Circle FFT 中的域减半步骤，我们在其中迭代地减小域大小。

8.1 引理 3 的陈述

该引理出现在 Circle STARKs 论文 中，用于形式化由平方映射启用的递归域减半。

假设 D 是大小为 2n 的 twin-coset（其中 n≥2）。那么应用平方映射 π(x,y)=(x2–y2,2xy) 将 D 转换为另一个大小为 2n−1 的 twin-coset π(D)。此外，如果 D 是一个标准位置陪集，那么 π(D) 也仍然是一个标准位置陪集。

直观地说，π 是一个群同态，它将子群 Gn−1 映射到 Gn−2。因此，大小为 2n 的 twin-coset 自然会产生另一个大小为 2n−1 的 twin-coset。

8.1.1 引理 3 证明的抽象视图

设 D 是大小为 2n 的 twin-coset，在抽象记号中这意味着

D=Q⋅Gn−1∪Q−1⋅Gn−1,

其中 |Gn−1|=2n−1。特别地，由于群同态，π 将子群 Gn−1 映射到 Gn−2 上。

π(D)=π(Q⋅Gn−1∪Q−1⋅Gn−1)=(π(Q)⋅Gn−2)∪(π(Q)−1⋅Gn−2).

这正是子群 Gn−2 中 twin-coset 的定义，其大小为 2n−2。因此，π(D) 本身是一个大小为 2n−1 的 twin-coset。

如果 D 最初是一个标准位置陪集，那么应用 π 会保留该标准位置属性，因为 π(Gn)=Gn−1。因此 π(D) 又是标准位置陪集，但现在大小为 2n−1。

8.2 手动计算示例（将大小为 8 的 Twin-Coset 减半为大小 4）

假设 p=31 并令 D 为大小为 23=8 的 twin-coset。具体来说，

D=Q⋅G2∪Q−1⋅G2，其中Q=(13,7).

由于 |G2|=4，我们有 |D|=8。我们检查 π 如何影响 D：

8.2.1 计算 π(Q) 和 π(Q−1)

π(Q)=(132–72,2⋅13⋅7)=(27,27), π(Q−1)=(27,4).

8.2.2 将 π 应用于 D

子群 G1 的大小为 2，比如 G1={(1,0),(30,0)}。根据引理 3，$$pi(D) = bigl(pi(Q)cdot G_1bigr) ;cup; bigl(pi(Q)^{-1}cdot G_1bigr).

–$π(Q)⋅(1,0)=(27,27)$–$π(Q)⋅(30,0)=(4,4)$–$π(Q−1)⋅(1,0)=(27,4)$–$π(Q−1)⋅(30,0)=(4,27)$

{(27,27),, (4,4)} ;cup; {(27,4),, (4,27)}

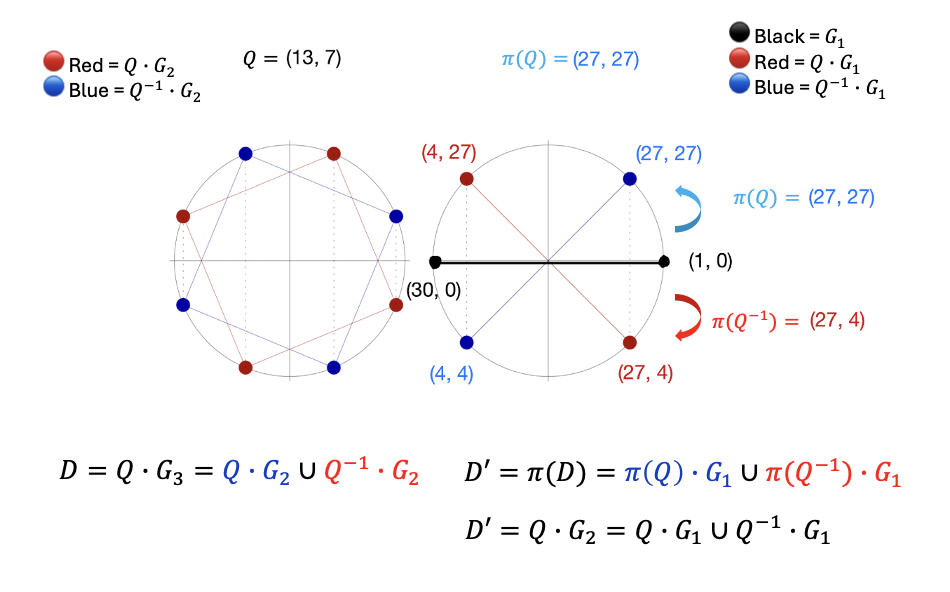
\$\$ 这是一个大小为 4 的 twin-coset。因此，π 将 D 从 8 个元素减半为 4 个，正如引理 3 所述。重复应用 π 会继续以 2 的幂收缩域，这在 Circle FFT 的递归结构中起着关键作用。在下图中：

• 左侧的圆显示了原始 twin-coset D=Q⋅G2∪Q−1⋅G2，其中 🔴 红色 = Q⋅G2，🔵 蓝色 = Q−1⋅G2。
• 右侧的圆显示了减半的 twin-coset π(D)，其中 🔵 蓝色 = π(Q)⋅G1，🔴 红色 = π(Q−1)⋅G1。
• ⚫ 黑色点标记子群 G1={(1,0),(30,0)}。

此视觉图说明了 π 如何通过群同态将大小为 $2^3=8$ 的原始域映射到大小为 22=4 的新 twin-coset 中。

9. 我们在第 1 部分中构建的内容

在本文中，我们重点介绍了如何将 Fp 上的圆曲线 x2+y2=1 转换为大小为 p+1 的循环群，并且我们讨论了具有具体示例的 twin-coset 和标准位置陪集。我们还展示了两个关键技术：一种用于将更大的标准位置陪集拆分为更小的 twin-coset，另一种用于通过应用平方映射将 twin-coset 的大小减半。这些技术共同使我们能够随意重塑大小为 2n 的域。

在下一部分中，我们将更深入地研究 Circle FFT 本身，展示这些 2n 大小的域（以及拆分或减半它们的能力）如何实现快速多项式评估和插值，即使当 p–1 的 2-adic 性不足时也是如此。

参考

• Circle STARKs https://eprint.iacr.org/2024/278
• Plonky3 https://github.com/Plonky3/Plonky3
• ZK11: Circle STARKs – Ulrich Haböck & Shahar Papini

ZK11: Circle STARKs - Ulrich Haböck & Shahar Papini - YouTube

• Circle STARKs: Part I, Mersenne https://blog.zksecurity.xyz/posts/circle-starks-1/
• Why I’m Excited By Circle Stark And Stwo

Why I’m Excited By Circle Stark And Stwo

• Exploring circle STARKs https://vitalik.eth.limo/general/2024/07/23/circlestarks.html
• An introduction to circle STARKs https://blog.lambdaclass.com/an-introduction-to-circle-starks/
• Yet another circle STARK tutorial https://research.chainsafe.io/blog/circle-starks/
• Deep dive into Circle-STARKs FFT https://ihagopian.com/posts/deep-dive-into-circle-starks-fft
• Coset’s Circle STARKs lecture videos

Overview of Circle STARKs - YouTube

• Ethereum/research/circlestark(Python implementation) https://github.com/ethereum/research/tree/master/circlestark
• Rust Implementation Demo of Circle Domain and Circle FFT

Rust Implementation Demo of Circle Domain and Circle FFT

https://github.com/0xxEric/CircleFFT

• STARKの原理 https://zenn.dev/qope/articles/8d60f77e3a7630

附录

下面，我们介绍圆曲线的射影视图与仿射视图，然后解释为什么 Circle STARK 特别选择素数 p≡3(mod4) 以避免像无穷远点这样的射影复杂性。

A.1 射影和仿射

在 Fp 上的仿射平面中，一个点简单地写为 (x,y)，其中 x,y∈Fp。相比之下，在射影平面 P2(Fp) 中，每个点都表示为 (X:Y:Z)，但所有非零标量倍数表示相同的位置。形式上，

$$ (X : Y : Z) ;equiv; (lambda X : lambda Y : lambda Z)quad (lambda neq 0). $$

圆 x2+y2=1 的射影模拟是

You can't use 'macro parameter character #' in math modeYou can't use 'macro parameter character #' in math mode

$$ X^2 + Y^2 ;=; Z^2. $$

在这里，如果 Z≠0，我们将 x=X/Z 和 y=Y/Z 视为 x2+y2=1 变为 X2+Y2=Z2。无穷远点是 Z=0 的任何解。是否存在这样的解取决于 −1 是否是 Fp 中的平方：

• 例如，如果 p≡1(mod4)，则 −1 是 Fp 中的平方。具体来说，存在一些 a 使得 a2≡−1(modp)，这意味着 X2+Y2≡0(modp) 可以在 Z=0 处具有非零 (X,Y)。这会在圆上产生额外的无穷远点，从而使群运算和实现复杂化。

示例：p=5

• 在这里，−1≡4 在 F5 中，4 确实是 (22)。
• 因此，X2+Y2≡0(mod5) 允许在 Z=0 时具有非零 (X,Y)，从而给出两个无穷远点。
• 仿射方程 x2+y2=1 恰好有四个仿射解：{(0,1),(0,4),(1,0),(4,0)}。
• 无穷远处的射影点是 {(2:1:0),(3:1:0)}，总共有 6 个解——与 p+1=6（仿射 4 + 无穷远 2）匹配。
• 如果 p≡3(mod4)，则 −1 不是 Fp 中的平方。因此，X2+Y2≡0(modp) 在 Z=0 处没有非零解。我们没有获得无穷远点，并且所有解都保持仿射。

示例：p=3

• 由于 −1≡2(mod3) 不是平方（我们有 12≡1 且 22≡1），因此在 Z=0 时没有 (X,Y) 满足 X2+Y2≡0。
• 然后，方程 x2+y2=1 仅具有仿射解。检查 x,y∈{0,1,2} 得出：{(0,1),(0,2),(1,0),(2,0)}，总共有 4 个解，与 p+1=4 匹配。

在 Circle STARK 中，我们特别选择 p≡3(mod4)，以便 −1 不是 Fp 中的平方。这确保我们的圆 x2+y2=1 没有无限（射影）点，从而使每个解都保持在仿射坐标中，并避免处理无穷远点的复杂性。

• 原文链接： rareskills.io/post/circl...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～