Orbital : 集中流动性的多稳定币池的自动化做市商

https://cdn.sanity.io/files/dgybcd83/production/7ed1ff02ff21d98961a4a50a3101b80ca2090329.mp4

1. 简介

未来会有数百万个稳定币。今天的的基础设施还没有准备好。

本文介绍了 Orbital，一个用于 2、3 或 10,$0$ 个稳定币池的自动化做市商。

Orbital 通过将集中的流动性带到更高的维度来释放资本效率。

2. 概述

https://cdn.sanity.io/files/dgybcd83/production/a7a5e8678f12c53c3a1823524feb5006b4bc8d6f.mp4

这是 USDC 和 USDT 之间的一个自动化做市商 (AMM) 的储备图。当交易者添加 USDT 时，他们会得到 USDC 作为回报。在中间，当储备相等时，这些币具有相同的价格。在边缘，与另一个相比，一个是毫无价值的。

https://cdn.sanity.io/files/dgybcd83/production/4223ca1f7af282d$0$1a3d7a7782c52f07c97d6d.mp4

Uniswap V3 开创了集中流动性的概念。它创建并合并了迷你 AMM，称为 ticks，通过将自己限制在仅指定的价位范围来支持以更少的资本进行更多的交易。Uniswap v3 允许流动性提供者在任意两个 tick 边界之间创建仓位，并有效地聚合他们的流动性，以便交易者可以像与单个池互动一样与之互动。但是，它仅支持两个资产之间的池。

Curve 创建了一个基于不变量的 AMM，允许在单个池中交易 N 个稳定币。它将流动性集中在价格 1 附近。但是，Curve 对每个池使用统一的策略，这意味着同一池中的所有流动性提供者都具有相同的流动性配置文件。

https://cdn.sanity.io/files/dgybcd83/production/3d122b2c3638529e338dc04e67c95dd868fae112.mp4

Orbital 通过围绕 $1 等价价格点绘制 tick 边界，将可定制的集中流动性扩展到三个或更多个稳定币的池。

与 2D 集中流动性不同，即使一个稳定币与 0 脱钩，Orbital tick 仍然可以以公平的价格交易其他稳定币。

https://cdn.sanity.io/files/dgybcd83/production/359bfd8e54fce9573b46a902c18c05a68b7a0dbe.mp4

更靠近 $1 等价价格点的较小 ticks 不需要持有储备资本，以防止其中一种币脱钩的情况。

这让 LP 可以将他们的资源集中在实际发生正常交易的地方，从而释放显著的资本效率收益。

https://cdn.sanity.io/files/dgybcd83/production/db2371755674bec8b4015fc05d0d8f223045d5f9.mp4

完整的 Orbital AMM 结合了不同大小的 ticks，因此 LP 可以自定义他们的风险敞口。

有些人可能会选择狭隘地关注 $1 点以实现最大效率，而另一些人可能会提供更广泛的覆盖范围，以便在波动时期赚取费用。

在底层，Orbital ticks 是 n 维球面帽。

由于对称性，我们可以将一些围绕其他旋转以获得单个环形（类似甜甜圈）的形状。

这使我们能够在链上高效地计算交易，而不管池中不同Coin的数量。

3. 直觉

下面的数学内容非常密集，但它只是试图将一个相对简单的视觉直觉形式化。

在上面描述的 3D 情况下，基础 Orbital AMM 是一个球体。我们在动画中只显示了球体的 1/8，因为它是在价格保持非负的情况下唯一相关的部分。

图中的 Orbital tick 指的是球体在红圈内部的部分。红圈本身构成了该 tick 的边界。请注意，与 Uniswap V3 不同，Orbital ticks 实际上是重叠的，因此较大的 ticks 完全包含较小的 ticks。

我们可以从动画中看到，一个 Orbital tick 可以处于两种状态之一。如果所有稳定币的价格都足够接近 $1 等价价格点，那么储备将位于内部 tick 的某个位置。但是，一旦价格差异足够大，该 tick 的储备将被钉在其边界上。

现在，假设我们有成百上千个 ticks。它们中的每一个要么是一个“内部 tick”，要么是一个“边界 tick”。

在局部，所有内部 ticks 的行为都类似于球体。由于它们在几何上相似，我们可以将它们全部合并，并将它们视为一个球体。

类似地，所有边界 ticks 在局部都表现得像圆圈（一般来说，在n 维度中，它们的行为类似于n-1维球体。由于它们在几何上相似，我们可以再次将它们全部合并，并将它们视为一个圆圈。

从逻辑上讲，我们现在处理的是一个球形 AMM 和一个圆形 AMM。通过围绕圆圈旋转球体，我们获得一个环面，或甜甜圈形状。

这个环面的方程足够简单，我们可以在链上有效地计算其表面上的交易。为了计算更大的交易，每次 tick 从边界变为内部或反之时，我们都会更新该方程。

幸运的是，所有这些在高维空间仍然成立，本文的其余部分将详细介绍其工作原理。

4. 机制

1. 球体 AMM

1. 公式

Orbital 是建立在球体 AMM 之上的

$$ |\vec{r}-\vec{x}|^2=\sum_{i=1}^n (r-x_i)^2 = r^2 $$

其中 $x_i$

是 AMM 的资产储备$i$。

要看到任何资产的最小储备是 $0$，请注意球体是以 $\vec{r} = (r, r, \dots, r)$ 为中心的，并且球体上的一个点在任何维度上离中心的距离最远可以是半径 $r$ 。

只要资产价格为正，无套利意味着我们永远不应该有储备

$x_i > r$ 对于任何 $i$ ，因为如果 $x_i=r+d$ 对于某些$d>0$ ，那么 $(r - x_i)^2 = d^2 = (r - (r - d))^2 = (r - (x_i - 2d))^2$

并且一些交易者可以免费移除 $2d$ 的资产 $i$ ，而不会影响 AMM 的恒定函数约束，并且根据假设，它将具有正值。因此，我们不会为 $x_i \leq r $ 向 AMM 添加显式约束，但可以假设 $x_i \leq r$ 在正常情况下对所有 $i$ 成立。

2. 球体上的 Token 价格

假设一个交易者想要给 AMM 一些 token $X_i$ 并取出一些 token $X_j$ ，同时保持在表面上 $F(\vec{x}) = |\vec{r} - \vec{x}|^2 = r^2$

在这种情况下，我们必须有

$$\frac{\delta F}{\delta x_i} \delta x_i + \frac{\delta F}{\delta x_j} \delta x_j = 0$$

因此，稍微滥用一下符号，我们可以将一单位 $x_j$的瞬时价格表示为 $$ \frac{\delta x_i}{\delta x_j} = -\frac{\delta F}{\delta x_j} / \frac{\delta F}{\delta x_i} = \frac{r - x_j}{r - x_i} $$

直观上，我们可以验证，如果 AMM 具有较高的 $X_j$ 储备和较低的 $X_i$ 储备，则该分数将很小，这意味着你从每单位 $X_j$ 获得的 $X_i$ 不多，反之亦然。

3. 等价价格点

我们的 AMM 表面上最重要的点是所有储备相等的点，因此，通过对称性，所有价格都相等。

这应该是稳定币的正常状态，因为在正常情况下，它们都应该值得它们盯住的价值，例如 \$1。

让我们将此点表示为 $\vec{q} = (q, q, \ldots, q)$

根据我们的球体约束，我们有

$$r^2 = |\vec{r} - \vec{q}|^2 = \sum_{i=1}^n (r - q)^2 = n(r - q)^2 $$

然后

$$(r - q)^2 = \frac{r^2}{n} \Rightarrow r - q = \frac{r}{\sqrt{n}}$$

因此

$$q = r\left(1 - \sqrt{\frac{1}{n}}\right)$$

我们有

$$ \vec{q} = r\left(1 - \sqrt{\frac{1}{n}}\right)(1, 1, \dots, 1)$$

由于它们都是

$$(1, 1, \dots, 1)$$

的倍数，因此存在一条从原点开始，经过等价价格点，到达 AMM 中心的线。我们可以使用单位向量来表示其方向

$$ \vec{v} = \frac{1}{\sqrt{n}} (1, 1, \dots, 1)$$

在交易方面，我们可以将 $$ \vec{v}$$ 视为一个由 每种币种 $\frac{1}{\sqrt{n}}$ 组成的投资组合。

4. 极坐标储备分解

本节介绍一个概念和符号，我们将在本文的其余部分中使用它们来处理 ticks。

给定 AMM 表面上的任何有效储备状态 $\vec{x}$ ，线性代数告诉我们，我们可以将其分解为与 $\vec{v}$ 平行的向量，以及与 $\vec{v}$ 正交的向量 $\vec{w}$，向量从原点到等价价格点。

换句话说，对于任何储备状态 $\vec{x}$ ，我们有

$ \vec{x} = \alpha \vec{v} + \vec{w} $ 其中 $ \quad \vec{v} \perp \vec{w} $

请注意，由于 $ \vec{v}$ 是单位向量，我们可以直接计算 $\alpha$ 为 $ \vec{x} \cdot \vec{v}$ ，它在机械上等于 $\frac{1}{\sqrt{n}} \sum_{i=1}^n — \frac{1}{\sqrt{n}}$ 乘以 $\vec{x}$ 中所有储备的总和。

通过这种分解的视角来看，我们的 AMM 约束变为

$$ r^2 = |\vec{x} - r|^2 = |(\alpha \vec{v} + \vec{w}) - r \cdot \vec{1}|^2 = |(\alpha \vec{v} + \vec{w}) - r \sqrt{n} \cdot \vec{v}|^2 = |(\alpha - r \sqrt{n}) \vec{v} + \vec{w}|^2 $$

由于 $\vec{v} \perp \vec{w}$

根据定义，我们可以使用毕达哥拉斯定理将其简化为

$$ r^2 = (\alpha - r\sqrt{n})^2 + |\vec{w}|^2$$

或者，重新排列，

$$ |\vec{w}|^2 = r^2 - (\alpha - r\sqrt{n})^2$$

由此，我们可以看到，如果我们使与 $ \vec{v} $

平行的储备分量保持不变，我们的 AMM 就像一个在与 $\vec{v}$ 正交的子空间中的低维球形 AMM，半径为 $s = \sqrt{r^2 - (\alpha - r\sqrt{n})^2}$

5. Tick 定义

1. 提示

为了简单起见，在本文的其余部分，我们将假设每个 tick 只有一个流动性提供者。当然，在实践中，我们将允许多个 LP 将其流动性汇集到同一个 tick 中，就像在 Uniswap V3 中一样。

提醒一下，Orbital 中的 ticks 是嵌套的。每个都以等价价格点为中心，并且较大的 ticks 与较小的 ticks 完全重叠。这与 Uniswap V3 形成对比，后者 ticks 是完全不相交的。

2. 几何直觉

我们可以从几何上将一个 tick 想象成球体表面上所有与等价价格点的测地线距离在某个固定距离之内的点。

在上面可视化的 3D 情况下，可以直观地了解到，我们可以通过用一个与向量 $\vec{v}$ 正交的平面切割球体来构造这样一个 tick 的边界，向量 $\vec{v}$ 是从等价价格点到球体中心的向量。

我们将在下面形式化这种针对更高维度的构造。

3. Tick 边界几何

任何与 $ \vec{v} = \left( \frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \dots, \frac{1}{\sqrt{n}} \right) \in \mathbb{R}^n $

垂直的平面具有以下形式 $\vec{x} \cdot \vec{v} = k$

这是另一种说法，即该平面精确地由其在 $\vec{v}$ 上的投影为 $k$ 的所有点组成 —— 即。 $ k\vec{v} + \vec{w}$ 形式的点，对于某些 $ \vec{w} \perp \vec{v}$ ，可以通过从 $ k\vec{v}$ 开始并添加一些与 $\vec{v}$ 垂直的向量来获得。

根据上面的极坐标储备分解部分，我们可以看到，当储备位于此边界上时，由于与 $\vec{v}$ 平行的储备分量在 $k\vec{v}$ 处是恒定的，该 tick AMM 在与 $\vec{v}$ 正交的 n-1 维子空间中，充当具有半径 $s = \sqrt{r^2 - (k - r\sqrt{n})^2}$ 和中心 $(k - r\sqrt{n})\vec{v}$ 的球形 AMM。

根据对称性，此边界上的每个点与等价价格点都具有相等的测地线距离。

6. Tick 大小边界

本节技术性较强，定义了有意义的最小和最大 ticks 的大小。

1. 最小 Tick

最小的 tick 边界将是等价价格点本身，我们在上面将其推导为点

$\vec{q}$ ，其中

$x_i = r\left(1 - \sqrt{\frac{1}{n}}\right)$

对于所有 $i$ 在这种情况下

$\vec{x} \cdot \vec{1} = r(n - \sqrt{n})$ ，由于 $ \vec{v} = \frac{1}{\sqrt{n}} \vec{1}$ ，我们可以使用平面常数定义此 tick

$k_{\text{min}} = \vec{x} \cdot \vec{v} = \frac{\vec{x} \cdot \vec{1}}{\sqrt{n}} = r(\sqrt{n} - 1)$

2. 最大 Tick

最大 tick 的边界由平面定义，该平面使我们能够实现可能的最高价值 $\vec{x} \cdot \vec{v}$ ，而不需要任何储备 $X_i$ 超过 $r$ 。当一个储备 $X_j$ 达到其最小值为 0，而所有其他储备都达到最大值 $r$ 时，就会发生这种情况。

例如，考虑 $x_1 = 0$ 和 $x_2 = x_3 = \cdots = x_n = r$ 。

因为它仍然在球面上，所以

$ \sum_{i=1}^n (r - xi)^2 = r^2 + \sum{i=2}^n (r - r)^2 = r^2$

我们有

$k_{\text{max}} = \vec{x} \cdot \vec{v} = \frac{0 + (n - 1)r}{\sqrt{n}} = r \frac{n - 1}{\sqrt{n}}$

要看到这确实是最大的 tick 边界，请注意，假设价格为正，除了 $X_1$ 之外的所有 token 的储备都已达到其最大值 $r$ 。因此，如果我们能增加 $\vec{x} \cdot \vec{v}$ 的唯一方法是增加 $X_1$ 的储备，同时减少其他储备的幅度较小，以免违反 AMM 常数。

但是请注意，$|\vec{r} - \vec{x}|^2$ 的梯度 $ 2(\vec{r} - \vec{x}) = (r, 0, \ldots, 0)$

在这一点上。因此，如果 AMM 无限小地减少其 $x_2$ 储备，由于 0 梯度，我们将根本不会降低 AMM 常数 $ |\vec{x} - r|^2$ 的值。这意味着我们无法增加 $x_1$ 来补偿，这确实是最大 tick 边界。

7. Tick 储备边界和虚拟储备

本节探讨了 tick 边界如何影响 tick 可以持有的最小和最大 token 储备，以及它对资本效率的影响。

1. 最小储备

考虑一个平面约束为 $ \vec{x} \cdot \vec{v} = k$ 的 Orbital tick。

让我们推导出任何一种币可能的最小储备，我们将其表示为 $X{\text{min}}$ 。根据对称性，所有其他 $X{\text{other}}$的储备在此时必须彼此相等。

然后，我们的球体约束变为

$(r - x{\text{min}})^2 + (n - 1)(r - x{\text{other}})^2 = r^2$

我们的平面不变量变为

$\frac{1}{\sqrt{n}} \left( (n - 1)x{\text{other}} + x{\text{min}} \right) = k$

因此

$x{\text{other}} = \frac{\sqrt{n}k - x{\text{min}}}{n - 1}$

求解所得的 $x_{\text{min}}$ 二次方程，我们得到

$x_{\text{min}} = \frac{k\sqrt{n} - \sqrt{k^2 n - n\left((n - 1)r - k\sqrt{n}\right)^2}}{n}$

在交易方面，这通常代表这样一种情况：除了一个币之外的所有币都与一个低值脱钩，导致交易者从 AMM 中取出尽可能多的仍然稳定的币。

2. 虚拟储备

无论交易者做什么，他们都不能强制任何 token $Xi$ 的储备下降到 $x{\text{min}}$ 以下。

这意味着创建 tick 的流动性提供者可以表现得好像他们拥有每个 tick 交易的稳定币的 $x{\text{min}}$ “虚拟储备”，并且在创建 tick 时实际上不需要提供那些 $x{\text{min}}$ token。与 Uniswap V3 中一样，这才是实现我们将在下面讨论的资本效率的原因。

3. 最大 Token 储备

我们可以重复上述推导，但翻转平方根的符号以找到假设两个约束都具有约束力的 tick 中任何给定币的最大数量。

由于如果价格为正，则没有币余额会超过 $r$ ，因此我们可以定义

$$x_{\text{max}} = \min\left(r, \frac{k\sqrt{n} + \sqrt{k^2 n - n\left((n - 1)r - k\sqrt{n}\right)^2}}{n}\right)$$

和

$$x{\text{other}} = \frac{\sqrt{n}k - x{\text{max}}}{n - 1}$$

在交易方面，这通常代表这样一种情况，即一种单一的币失去其Hook并贬值，而其他币保持稳定，从而导致交易者向 AMM 提供尽可能多的那种币。我们称之为单一脱钩事件。

8. 解读 k

如果我们假设事情“出错”的最常见方式是上面立即描述的单一脱钩事件类型，那么对于足够小的 $k$，我们正在集中流动性，而没有币已经贬值到某个阈值以下 —— 例如，没有币已经贬值到低于 99 美分的区域。

假设只有一个币脱钩，而其余币保持不变，并且 $k$ 足够小，以至于平面约束具有约束力，则脱钩币将具有

$$ x_{\text{depeg}} = \frac{k\sqrt{n} + \sqrt{k^2 n - n\left((n - 1)r - k\sqrt{n}\right)^2}}{n}$$

的储备和

$$x{\text{other}} = \frac{k\sqrt{n} - x{\text{depeg}}}{n - 1}$$

回想一下定价部分，token $X_j$ 相对于 token $X_i$ 的瞬时价格为

$$\frac{\delta x_i}{\delta x_j} = -\frac{\delta F}{\delta x_j} \bigg/ \frac{\delta F}{\delta x_i} = \frac{r - x_j}{r - x_i} $$

在这种情况下，tick 边界对应于 token 单一脱钩到

$$p{\text{depeg}} = \frac{r - x{\text{depeg}}}{r - x_{\text{other}}}$$

然后，我们可以反转此结果以获得对于给定的 $$p_{\text{depeg}}$$ ，在那个脱钩价格恰好激活的 $k$：

$$ k{\text{depeg}}(p{\text{depeg}}) = r\sqrt{n} - \frac{r(p{\text{depeg}} + n - 1)}{\sqrt{n(p{\text{depeg}}^2 + n - 1)}}$$

请注意，对于足够大的 $k$ ，例如 $k_{\text{max}}$ ，当多个币都完全脱钩到 0 时，tick 将保持完全在范围内，因此这种解释在那里并不相关，我们最好考虑诸如假设除了一个币之外的所有币都脱钩的最大投资组合损失之类的指标。

9. 资本效率

正如我们上面推导的那样，给定一个平面常数 $k$ ，给定 tick 的 LP 可以利用虚拟储备

$$x_{\text{min}}(k) = \frac{k\sqrt{n} - \sqrt{k^2 n - n\left((n - 1)r - k\sqrt{n}\right)^2}}{n}$$

对于每个 n 资产。如果我们假设他们在储备处于等价价格点 $\vec{q}$ 时创建 AMM，那么他们需要为球形 AMM 中的每种币提供的储备将为

$$x_{\text{base}} = r\left(1 - \sqrt{\frac{1}{n}}\right)$$

因此，假设价格永远不会出现足够大的差异，以至于将储备推过 tick 边界，那么资本效率的增益为

$$ \frac{x{\text{base}}}{x{\text{base}} - x_{\text{min}}(k)}$$ 使用前一节中的 depeg 价格公式，我们可以计算出通过选择对应于最大 depeg 价格的边界，你能获得多少资本效率 $p$:

$$ c{\text{efficiency}}(p) = \frac{x{\text{base}}}{x{\text{base}} - x{\text{min}}(k_{\text{depeg}}(p))}$$

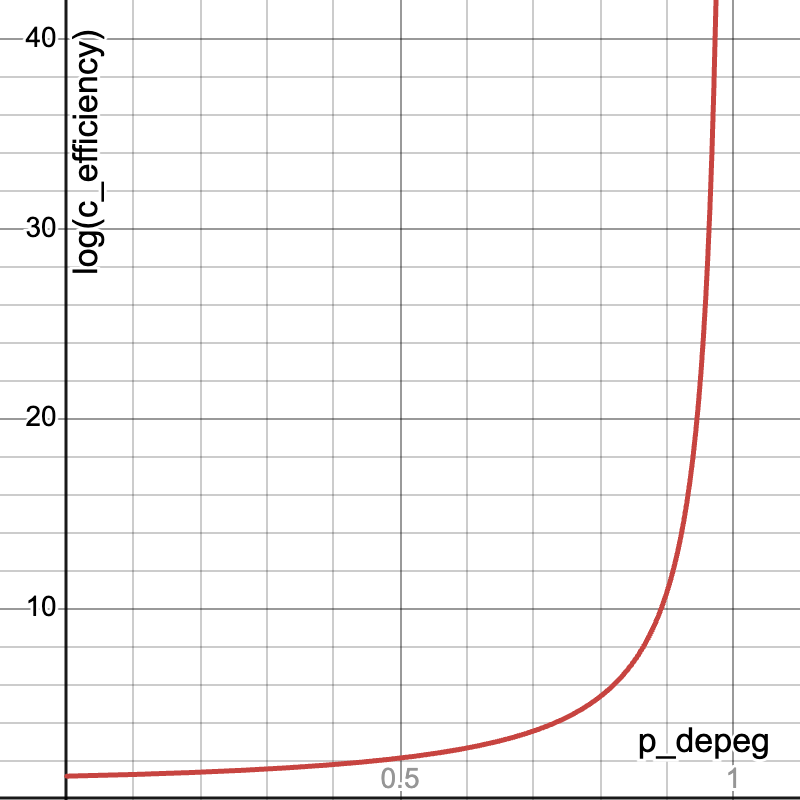
n=5 时的对数资本效率比率与 Depeg 价格的关系

例如，在 5 资产的情况下，0.90 美元的 depeg 限制对应于大约 15 倍的资本效率增加，而 0.99 美元的限制对应于大约 150 倍的资本效率增加。

你可以在 Desmos 上查看交互式图表 here.

Tick 合并

概述

一个完整的 Orbital AMM 由多个具有不同 $k$ 值的 Orbital tick 组成。

在本节中，我们将讨论为了进行交易计算，可以将多个 tick 视为一个 tick 的情况。这将为我们构建下一个部分中整个 orbital AMM 的全局交易不变量做好准备。

提醒一下，为了简单起见，我们将假设每个 tick 只有一个 LP。

合并数学

假设我们有两个 tick，$T_a$ 和 $T_b$ ，它们的储备金为 $\vec{x}_a$ 和 $\vec{x}_b$ ，参数分别为 $(r_a, ka)$ 和 $(r{b}, k_{b})$ 。

情况 1：两个储备金都在内部

最简单的情况是，两个储备金向量的交易开始和结束都在各自 tick 的“内部”，也就是说，不在 tick 边界上 -- 即 $$ \vec{x}_a \cdot \vec{v} < k_a \quad \text{and} \quad \vec{x}_b \cdot \vec{v} < k_b $$

在这种情况下，两个 tick 在本地的行为都像正常的球面 AMM，并且必须是 $\vec{r}_a - \vec{x}_a$ 与 $\vec{r}_b - \vec{x}_b$ 平行，因为否则至少有一个 $X_i$ 相对于某个 $X_j$ 在两个 AMM 上的价格会有所不同，从而允许套利。

由于根据定义 $ \vec{r}_a = r_a \sqrt{n} \vec{v}$ 和 $ \vec{r}_b = r_b \sqrt{n} \vec{v} $，我们可以看到 $\vec{r}_a - \vec{x}_a$ 与 $\vec{r}_b - \vec{x}_b$平行，当且仅当

$\vec{x}_a = \frac{r_a}{r_b} \vec{x}_b$

这意味着两个 AMM 的总储备金等于

$$ \vec{x}_a + \vec{x}_b = \left(1 + \frac{r_a}{r_b}\right) \vec{x}_b = (r_a + r_b) \frac{\vec{x}_b}{|\vec{x}_b|}$$

由于我们的 AMM 常数为 $|\vec{x}| = r$ ，我们可以看到储备金与 AMM 的半径成比例，因此在本地，我们可以将两个 tick 视为一个球面 AMM，其 $r_c = r_a + r_b$ 只要其中一个储备金向量达到其点位的边界，我们就不能再将两个点位视为一个球面 AMM，而必须转到后面的情况之一。

情况 2：两个储备金都在边界上

假设两个 tick 都以位于其边界上的储备金开始，边界由其平面常数定义。

现在假设它们执行一个交易 $\vec{\Delta}$ ，使得它们的储备金从 $\vec{x}$ 变为 $ \vec{x}' = \vec{x} + \vec{\Delta}$ ，之后它们仍然在它们的边界上。

在这种情况下，对于 tick $A$ ，我们有

$$ \vec{x}_a \cdot \vec{v} = k_a \quad \text{and} \quad \vec{x}'_a \cdot \vec{v} = (\vec{x}_a + \vec{\Delta}_a) \cdot \vec{v} = k_a + \vec{\Delta}_a \cdot \vec{v} = k_a \Rightarrow \vec{\Delta}_a \cdot \vec{v} = 0$$

这意味着交易向量 $\vec{\Delta}_a$ 必须正交于 $\vec{v}$ 如果 tick 储备金都在边界上开始和结束，那么 $\vec{\Delta}_b$ 也必须如此。换句话说，这个交易完全在正交于 $\vec{v}$ 的子空间内。

正如我们在关于 tick 边界几何的部分中讨论的，边界上的 tick 在正交于 $\vec{v}$ 的子空间中表现得像球面 AMM。因为两个 AMM 的中心都平行于 $\vec{v}$ ，它正交于该子空间中的每个向量，我们可以将这个子空间 AMM 视为具有中心 $0$ ，并且通过与情况 1 类似的逻辑，它具有半径

$s_c = s_a + s_b$

其中从关于 tick 边界几何的部分中，我们有例如

$s_a = \sqrt{r_a^2 - (k_a - r_a\sqrt{n})^2}$

全局交易不变量

本节介绍如何使用我们所有的 tick 同时在本地计算交易。 它是非常密集的。 如果你想解析它，你最喜欢的 LLM 可能会有所帮助。

设置(setup)

首先，请注意，上面的 tick 合并部分表明，我们可以将所有当前内部的 tick 合并到一个 $\mathbb{R}^n$ 中的单个球形 tick 中，并将所有当前边界上的 tick 合并到与 $\vec{v}$ 正交的 $\mathbb{R}^n$ 子空间中的另一个球形 tick 中。 因此，在本节的其余部分，我们将假设我们恰好有两个 tick，一个内部和一个边界。

我们将我们组合的 Orbital AMM 的总储备金向量称为 $ \vec{x}_{\text{total}}$ 。正如在极坐标储备金分解部分中描述的，我们可以将其分解为平行于 $\vec{v} = \frac{1}{\sqrt{n}} (1, 1, \dots, 1)$ 和正交于 $\vec{v} = \frac{1}{\sqrt{n}} (1, 1, \dots, 1)$ 的分量，因此

$$ \vec{x}{\text{total}} = \alpha{\text{total}} \vec{v} + \vec{w}_{\text{total}}$$

对于某些 $\vec{w}_{\text{total}} \perp \vec{v}$ 。

我们对我们的合并和边界 tick 做同样的处理：

$ \vec{x}{\text{int}} = \alpha{\text{int}} \vec{v} + \vec{w}_{\text{int}}$

$\vec{x}{\text{bound}} = \alpha{\text{bound}} \vec{v} + \vec{w}_{\text{bound}}$

并且因为 $x{\text{total}} = x{\text{int}} + x_{\text{bound}} $，我们必须有

$a{\text{total}} = \alpha{\text{int}} + \alpha_{\text{bound}}$

$ \vec{w}{\text{total}} = \vec{w}{\text{int}} + \vec{w}_{\text{bound}}$

寻找 alpha_bound 和 alpha_int

我们知道边界储备金 $ \vec{x}_{\text{bound}}$ 必须满足

$\vec{x}{\text{bound}} \cdot \vec{v} = k{\text{bound}}$

根据定义，因为边界 AMM 始终使其储备金位于由其平面约束定义的边界上。

通过极坐标储备金分解，我们还有

$ \vec{x}{\text{bound}} \cdot \vec{v} = (\alpha{\text{bound}} \vec{v} + \vec{w}{\text{bound}}) \cdot \vec{v} = \alpha{\text{bound}}$

因此

$\alpha{\text{bound}} = k{\text{bound}}$

因为

$\alpha{\text{total}} = \alpha{\text{int}} + \alpha_{\text{bound}} $

然后我们有

$ \alpha{\text{int}} = \alpha{\text{total}} - \alpha{\text{bound}} = \vec{x}{\text{total}} \cdot \vec{v} - k_{\text{bound}}$

证明 w_int 和 w_bound 是平行的

为正交于 $\vec{v}$ 的子空间构造一个标准正交基

$ \vec{z}1, \ldots, \vec{z}{n-1}$ 。 与 $\vec{v}$ 一起，这构成了我们整个储备金空间的标准正交基，其中每个基元素代表不同比例的组成稳定币的一篮子货币。

由于这只是轴的旋转，我们的内部 tick 仍然是所有这些新基向量之间的球面 AMM，而我们的边界 tick，作为正交于 $\vec{v}$ 的子空间中的球面 AMM，是该子空间的所有基向量之间的球面 AMM， $ \vec{z}1, \ldots, \vec{z}{n-1}$ 。

由此，我们可以看到内部 tick 和边界 tick 必须持有 $ \vec{z}_i$ 相同的比例，因为否则会有一些 $i$ 和 $j$，其中组合$\vec{z}_i$ 的价格与边界和内部 tick 上的组合 $\vec{z}_j$ 的价格不同，这将带来套利机会。

由于 $\vec{z}i$ 构成了储备金空间正交于 $\vec{v}$ 的子空间的完整基础，这表明$\vec{w}{\text{int}}$ 实际上必须平行于 $\vec{w}_{\text{bound}}$ 。

寻找 ||w_int||

回想一下关于 tick 边界几何的部分，

$$ |\vec{w}{\text{bound}}|^2 = s{\text{bound}}^2 = r{\text{bound}}^2 - (k{\text{bound}} - r_{\text{bound}} \sqrt{n})^2$$

由于，正如我们在上一小节中证明的，$\vec{w}{\text{int}}$ 平行于 $\vec{w}{\text{bound}}$，它们总和的长度只是它们长度的总和，因此

$$ |\vec{w}{\text{total}}| = |\vec{w}{\text{int}}| + |\vec{w}_{\text{bound}}|$$

代入，我们然后获得

$$ |\vec{w}{\text{int}}| = |\vec{w}{\text{total}}| - |\vec{w}{\text{bound}}| = |\vec{x}{\text{total}} - (\vec{x}{\text{total}} \cdot \vec{v}) \vec{v}| - \sqrt{r{\text{bound}}^2 - (k{\text{bound}} - r{\text{bound}} \sqrt{n})^2} $$

完整的 不变量

我们内部 tick 的球面不变量是

$$ r{\text{int}}^2 = |\vec{r}{\text{int}} - \vec{x}_{\text{int}}|^2$$

通过勾股定理，这意味着

$$ r{\text{int}}^2 = |\vec{r}{\text{int}} - \alpha{\int} \vec{v}|^2 + |\vec{w}{\text{int}}|^2 = (\alpha{\text{int}} - r{\text{int}} \sqrt{n})^2 |\vec{v}|^2 + |\vec{w}_{\text{int}}|^2 $$

代入我们从前面部分得到的结果并简化，我们然后获得完整的 不变量

$$ 2r{\text{int}}^2 = \left((\vec{x}{\text{total}} \cdot \vec{v} - k{\text{bound}}) - r{\text{int}} \sqrt{n}\right)^2

• \left(|\vec{x}{\text{total}} - (\vec{x}{\text{total}} \cdot \vec{v}) \vec{v}|
• \sqrt{r{\text{bound}}^2 - (k{\text{bound}} - r_{\text{bound}} \sqrt{n})^2}\right)^2 $$

注意，这等效于广义环面的公式，即熟悉的多纳圈形状的更高维扩展。 直观地说，这是因为我们将内部 tick（一个完整的球体）的流动性与边界 tick（子空间中的较低维球体）的流动性“加在一起”，就像通过将一个球体居中在圆上的每个点来构造一个多纳圈一样。

计算

我们可以直接将这个 不变量计算为

$$ r{\text{int}}^2 = \left( \frac{1}{\sqrt{n}} \sum{i=1}^n x{\text{int}i} - k{\text{bound}} - r_{\text{int}} \sqrt{n} \right)^2

• \left( \sqrt{ \sum{i=1}^n x{\text{total}i}^2 - \frac{1}{n} \left( \sum{i=1}^n x{\text{total}i} \right)^2 }
• \sqrt{ r{\text{bound}}^2 - (k{\text{bound}} - r_{\text{bound}} \sqrt{n})^2 } \right)^2 $$

orbital 的实现应跟踪该表达式中出现的储备金总和和平方储备金总和。

由于一个代币换另一个代币的交易仅影响这些总和中的两个项，因此我们可以以恒定的时间计算交易的 不变量，而与维度数无关 n 。

在 Tick 边界内交易

逻辑

现在我们有了全局交易不变量，计算交易就变得很简单了。

假设用户提供 $d$ 个单位的资产 $i$ 给 AMM，并希望将其兑换成尽可能多的资产 $j$ 。

从一些有效的储备金状态开始 $\vec{x}_{\text{total}}$ ，我们只需将 $X_i$ 的值更新为 $x_i + d$ ，然后求解满足全局不变量的 $X_j$ ，同时保持所有其他资产余额不变。 如果有多个解，我们选择一个使 $X_j$ 的最终余额低于内部和边界 tick 的中心的解。

这是关于 $X_j$ 的四次方程，我们可以使用牛顿法在链上轻松求解。 如上所述，如果我们显式跟踪 AMM 中的总和，则无论 AMM 中的维度数如何，方程的复杂度都保持恒定。

跨越 Ticks

我们在上一节中导出的全局交易不变量假设 ticks 保持其作为“内部”或“边界”的状态。

但是，在交易期间，系统的状态可能会发生变化，从而导致先前内部 tick 的储备金被锁定在其边界上（反之亦然）。 在这种情况下，我们需要从合并的边界（内部）tick 中删除该 tick，并将其添加到合并的内部（边界）tick 中，然后相应地更新环面公式。

在本节中，我们将解释如何检测何时发生这些交叉以及如何通过将导致它们的交易分解为多个段来处理它们。

直觉

想象一下，我们有几个不同大小的 ticks，每个 tick 都是一个球体，与由该 tick 的平面常数确定的平面相交。 这些球体的大小可能因其各自的半径而异，但我们可以想象“放大”或“缩小”球体，以便它们看起来都具有相同的大小，也许由半径 1 表示。

如果我们这样做，我们会看到一些有趣的事情：所有当前“内部”的 ticks，即所有储备金没有完全在其平面边界上的 ticks，似乎它们的储备金位于球体上的完全相同的点上。 从几何上讲，我们可以说这是因为球体是相似的。 从交易的角度来看，正如上面所说的那样，我们可以说这是因为否则 ticks 之间就会存在套利机会。

此外，ticks 会将其储备金困在其平面边界上并成为边界 ticks，恰恰是在这个共同储备金点偏离等价价格点比该 tick 的平面边界更远时。

因此，为了跨 ticks 进行交易，我们只需计算交易，假设如上面关于 tick 内交易的部分所述，没有 ticks 从内部移动到边界。 然后，我们检查新的共同内部储备金点，并查看它是否已越过最接近的内部 tick 或最接近的边界 tick 的平面边界。 如果是这样，我们将交易精确地计算到该边界点，更新已交叉的 tick 的类型，并计算交易的其余部分。

规范化 Normalization

我们通过将 ticks 半径除以不同大小的 ticks 来使用规范化量来比较 ticks。

规范化位置 是 $x^{\text{norm}} = \vec{x} / r$

规范化投影 是 $ a^{\text{norm}} = \vec{x}^{\text{norm}} \cdot \vec{v} = \frac{\vec{x} \cdot \vec{v}}{r}$

规范化边界 是 $k^{\text{norm}} = \frac{k}{r}$

请注意，如果 $\alpha^{\text{norm}} = k^{\text{norm}}$

对于给定的 tick，我们可以将两边乘以 $r$ 以删除规范化并查看该 tick 是否在其边界上。

假设对于给定的 tick，我们有 $\alpha^{\text{norm}} < k^{\text{norm}}$ ，因此它是一个内部 tick。 通过无套利，其储备金向量 $\vec{x}$ 将平行于所有其他内部 ticks 的储备金向量，因此其规范化储备金向量 $\vec{x}^{\text{norm}}$ 将精确地等于所有内部 ticks 的规范化储备金向量，我们将其称为 $ \vec{x}^{\text{norm}}_{\text{int}}$ 。

该内部规范化储备金向量具有投影

$\alpha^{\text{norm}}{\text{int}} = \vec{x}^{\text{norm}}{\text{int}} \cdot \vec{v}$ 给定的 tick $i$

是内部的，当且仅当 $k^{\text{norm}}i > \alpha^{\text{norm}}{\text{int}}$ 。 要查看原因，首先假设 $i$ 是内部的。 然后根据定义 $ k^{\text{norm}}_i > \alpha^{\text{norm}}i = \alpha^{\text{norm}}{\text{int}}$ 。 对于另一个方向，假设 $k^{\text{norm}}i > \alpha^{\text{norm}}{\text{int}}$ 。 然后，如果此 tick 与内部 tick 具有相同的规范化位置，则它不会达到其平面约束，这意味着通过无套利，它实际上必须具有此规范化位置，使其成为内部 tick。

交易分段流程

在任何给定时间，AMM 在 tick 空间中的位置都由

$ k{\text{int}}^{\text{min}}$ 表示，这是当前内部 tick 的最小规范化 $k$ ，如果整体预留金继续远离相等的价点，这将是下一个被困在其边界的点。 类似地， $k{\text{bound}}^{\text{max}}$ 是当前边界 tick 的最大规范化 $k$ ，这将是在 AMM 预留金恢复到相等的价格点时再次变为内部的第一个点。

假设我们正在尝试计算交易 $\vec{\Delta}_{\text{total}}$ ，其中用户投入一些数量 $d_i^{\text{total}}$ 的资产 $X_i$ 以移除一些资产 $X_j$ 。 分段交易的步骤如下：

计算假设没有 Tick 边界交叉： 假设所有当前内部 tick 保持内部，所有当前边界 tick 保持边界，并使用上面的全局交易不变量方法计算潜在的最终 AMM 状态 $\vec{x}{\text{potential}}$ 和相应的内部 tick 规范化投影 $\alpha{\text{int}}^{\text{norm}}$。

边界交叉检查： 如果我们的假设是正确的，并且没有 ticks 从内部更改为边界，反之亦然，那么我们将拥有

$k{\text{bound}}^{\text{max}} \leq \alpha{\text{int}}^{\text{norm}} \leq k_{\text{int}}^{\text{min}}$

-- 即我们的新内部 tick 点将所有内部 tick 边界与所有边界 tick 边界分开。

如果是这种情况，我们就完成了。 否则，我们需要分段交易。

如果检测到交叉则进行分段

我们知道从上一步交叉的规范化边界，我们将其称为 $k{\text{cross}}^{\text{norm}}$ 。 当 $ \alpha{\text{int}}^{\text{norm}} = k{\text{cross}}^{\text{norm}} \Rightarrow \alpha{\text{int}} = r{\text{int}} k{\text{cross}}^{\text{norm}}$ 时，将发生此交叉。

所以然后在交叉点，我们有

$$ \alpha{\text{crossover}} = \vec{x} \cdot \vec{v} = \vec{x}{\text{int}} \cdot \vec{v} + \vec{x}{\text{bound}} \cdot \vec{v} = \alpha{\text{int}} + k{\text{bound}}^{\text{total}} = r{\text{int}} k{\text{crossover}}^{\text{norm}} + x{\text{bound}}^{\text{total}} $$

其中 $k_{\text{bound}}^{\text{total}}$ 是所有当前边界 ticks 的 $k$ 值的总和。

查找交叉交易 $\vec{\Delta}_{\text{crossover}}$

我们想要找到交易

$ \vec{\Delta}_{\text{crossover}} = (0, \ldots, d_i^{\text{crossover}}, 0, \ldots, -d_j^{\text{crossover}}, 0, \ldots) $

在 $i$ 和 $j$ 之间，这尊重全局不变量，同时将我们精确地带到交叉点 $ \vec{x}{\text{crossover}} = \vec{x} + \vec{\Delta}{\text{crossover}} $ 其中我们有

$$ \alpha{\text{crossover}} = \vec{x}{\text{crossover}} \cdot \vec{v} = (\vec{x} + \vec{\Delta}{\text{crossover}}) \cdot \vec{v} = \alpha{\text{total}} + \vec{\Delta}{\text{crossover}} \cdot \vec{v} \ = \alpha{\text{total}} + \frac{1}{\sqrt{n}}(d_i^{\text{crossover}} - d_j^{\text{crossover}}) $$

因此我们看到

$$ dj^\text{crossover} = \sqrt{n} (\alpha\text{total} - \alpha_\text{crossover}) + d_i^\text{crossover} $$

将其代入上面的全局不变量公式会得到关于

$$ d_i^{\text{crossover}} $$

的二次方程，我们可以使用二次公式简单地求解该方程。一旦我们找到交叉点，我们就可以执行交易到那里，调整从内部到边界或从边界到内部的交叉 tick，并继续进行剩余的交易，并在必要时重新分段。

结论

今天，Orbital 只是一个设计，但我们很高兴看到它将如何改变稳定币流动性格局。

如果你有兴趣与我们一起探索，我们很乐意听取你的意见。

• 原文链接： paradigm.xyz/2025/06/orb...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～