基于密码学的安全联邦学习

边缘数据生成的指数级增长在现代机器学习中造成了一种根本性的紧张关系。虽然中心化的数据聚合能够实现强大的模型训练，但它与隐私法规、数据主权要求以及传输海量数据集的不切实际性相冲突。联邦学习 通过颠倒传统工作流程来解决这个问题：不是将数据移动到模型，而是将模型移动到数据。

在联邦学习中，多个参与方在保持数据本地化的同时，协同训练一个共享模型。一个中央协调器将模型参数分发给客户端，客户端在本地进行训练，并且只返回模型更新、梯度或权重。服务器聚合这些更新以改进全局模型，从而使医疗机构、金融组织和移动设备能够在不暴露敏感数据的情况下进行协作。

然而，简单的实现仍然容易受到攻击。模型更新可能会受到成员推理和模型反演攻击的攻击，而投毒攻击可能会损害完整性。这些漏洞需要一个全面的密码学框架。

本文探讨了安全联邦学习的密码学基础。我们专注于水平联邦学习（共享特征，不同的样本）。我们的安全框架解决了三个要求：更新的机密性、针对恶意参与者的鲁棒性以及计算的可验证性。

我们探索同态加密，特别是像 Paillier 这样的部分同态方案以提高资源效率，以及用于端到端隐私场景的全同态加密。我们分析了安全多方计算协议，这些协议以通信开销为代价来分配信任。最后，我们介绍了用于可验证聚合的零知识证明。

联邦学习：框架与基础

联邦学习 允许多个参与方协同训练一个共享模型，同时保持训练数据分布在各个参与设备或机构中。模型不是集中整合数据，而是传输到数据，在本地进行训练，并且只有模型更新返回到协调服务器。这种方法解决了数据对隐私敏感或难以集中的场景：移动设备、医院和金融机构都可以在不暴露原始数据集的情况下参与协作训练。

数据分布分类

联邦学习 系统按数据在参与者中的分布方式进行分类：

水平联邦学习 (Horizontal Federated Learning): 参与者共享相同的特征空间但具有不同的样本 ID 空间。当相似的实体为不同的人群提供服务时，就会发生这种情况：拥有不同患者群体的区域医院、位于不同市场的银行或由不同用户拥有的移动设备。由于所有参与者都使用相同的特征表示，因此模型可以通过参数平均自然地聚合。

垂直联邦学习 (Vertical Federated Learning): 数据集共享相同的样本 ID 空间但在特征空间中有所不同。例如，同一城市中的一家银行和一家电子商务公司拥有重叠的用户集，但银行记录金融行为，而电子商务公司保留购买历史记录。这种不对称结构需要更复杂的安全聚合协议。

联邦迁移学习 (Federated Transfer Learning): 数据集在特征空间和样本空间中都不同，且重叠最少。使用有限的公共样本学习公共表示，并将其应用于具有单边特征的样本的预测。这使得跨相关但不同领域的协作成为可能。

中心化架构

在中心化联邦学习中，单个协调服务器协调 $K$ 个参与客户端的训练。训练以迭代方式进行，包括四个阶段：客户端选择、本地训练、更新传输和全局聚合。服务器每轮抽取一部分客户端，以解决带宽限制和设备可用性问题。选定的客户端接收当前模型参数，对其私有数据执行本地训练，并将更新传回服务器。服务器聚合这些更新，以生成改进的全局模型，用于下一轮训练。

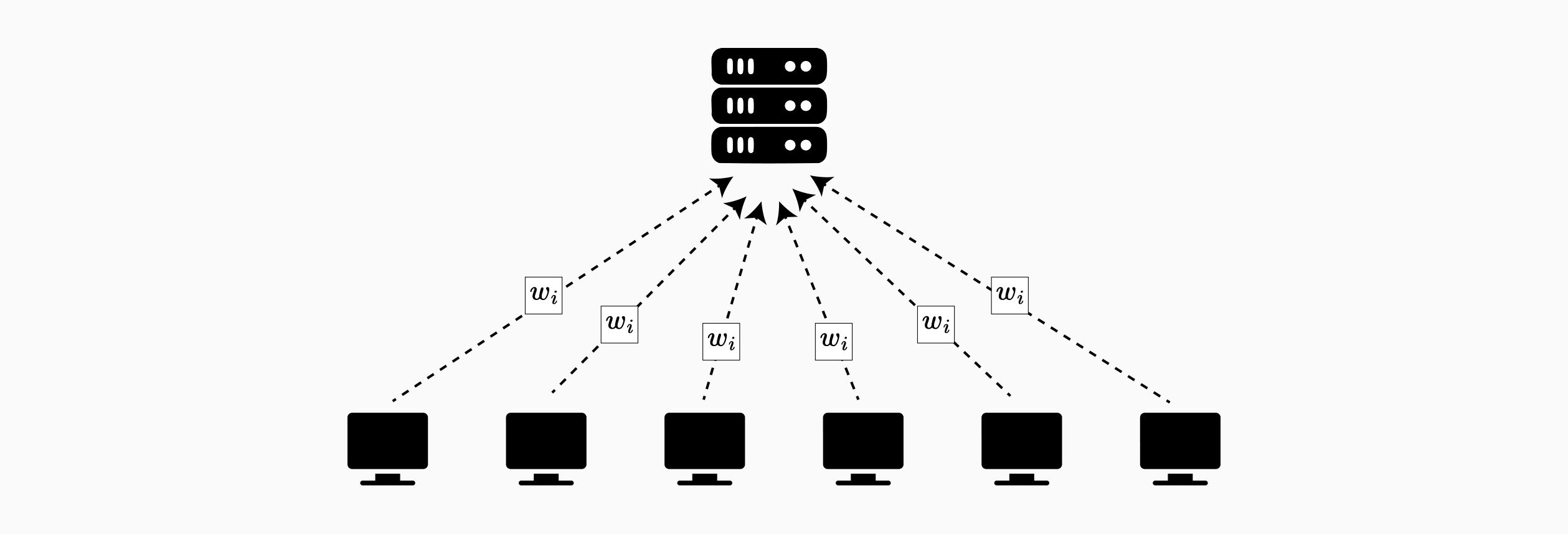
分布式架构

在分布式联邦学习中，中央协调器被分布式协调机制取代，该机制通常通过区块链智能合约或点对点协议来实现。客户端不是依赖于单个受信任的服务器，而是直接与不可变的账本或分布式网络交互，该账本或分布式网络强制执行训练协议。客户端在链上注册其参与情况，向区块链提交加密或屏蔽的模型更新，并且聚合逻辑在智能合约中自动执行。此架构消除了单点故障，并消除了对中央聚合器的信任假设。但是，去中心化带来了额外的挑战：区块链交易成本（gas 费用）、共识机制的延迟以及所有参与者都需要验证计算。权衡的是中心化系统的信任假设与去中心化替代方案中分布式共识的开销。

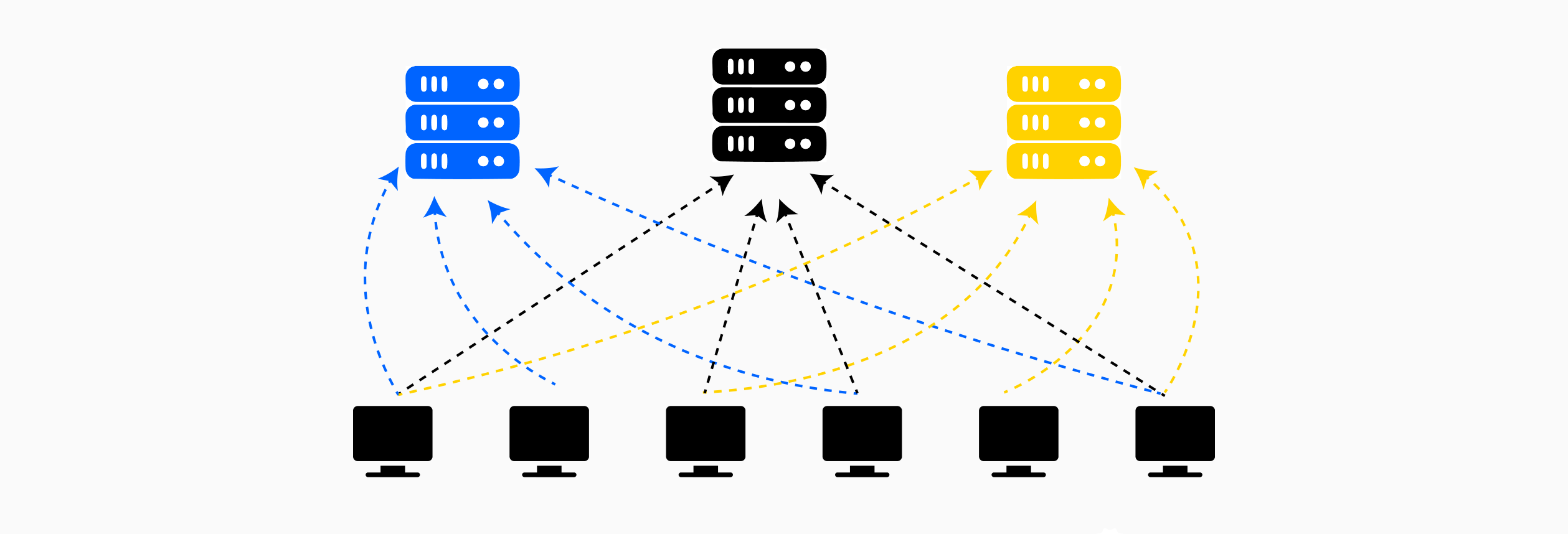
联邦平均 (Federated Averaging)：基础算法

联邦平均 (FedAvg) 是水平联邦学习的基础方法，它将本地随机梯度下降与周期性模型平均相结合，以实现通信高效的分布式训练。关键创新在于允许在通信之前执行多个本地更新步骤，与同步随机梯度下降相比，所需通信轮数减少了 10-100 倍。

算法步骤：

1. 服务器初始化： 服务器初始化全局模型参数 $w_0$ 并选择超参数：本地 epoch 数 $E$、mini-batch 大小 $B$ 和学习率 $\eta$。
2. 客户端选择： 在每一轮 $t$ 中，服务器抽取可用客户端的子集以参与训练。
3. 模型分发： 选定的客户端接收当前的全局模型参数 $w_t$。
4. 本地训练： 每个客户端 $k$ 在其本地数据集上执行 $E$ 个 epoch 的随机梯度下降，计算更新后的模型参数 $w_k$。
5. 更新传输： 客户端将其完整的更新后的模型参数发送回服务器。
6. 加权聚合： 服务器对接收到的模型执行加权平均，其中每个客户端的贡献与其训练示例的数量成比例地加权，从而生成新的全局模型 $w_{t+1}$。
7. 迭代： 重复步骤 2-6，直到收敛或达到最大轮数。

安全问题

虽然联邦学习避免了传输原始数据，但模型更新本身、梯度或权重变化会泄漏关于底层训练数据的大量信息。即使客户端仅共享参数更新而不是其数据集，也可以通过基于梯度的攻击来利用这些更新来推断敏感属性或重建训练样本。这就需要用于安全传输和聚合更新的机制，以确保在整个联邦学习管道中的机密性。

通过掩码进行安全聚合

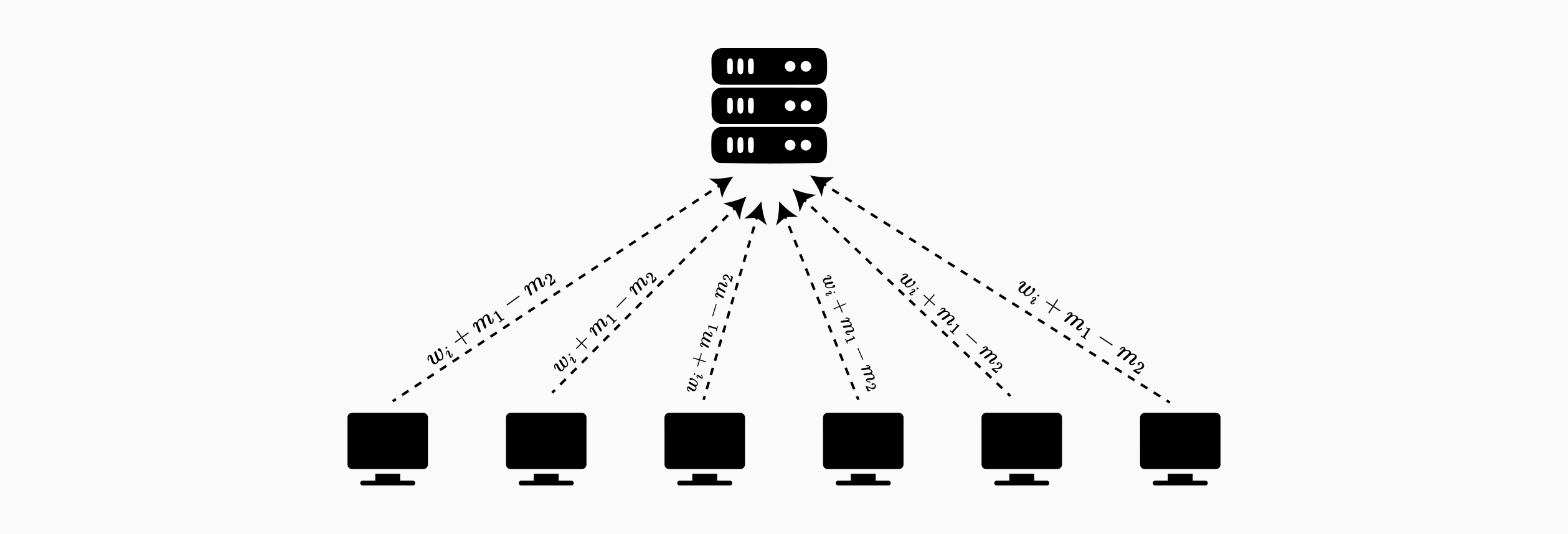
SMPAI 协议演示了联邦学习的基础方法。核心机制依赖于成对密钥共享：每对客户端建立共享随机性，该随机性在传输期间屏蔽其各自的权重。聚合器可以计算屏蔽值的总和，但是随机掩码在聚合中会抵消，从而仅显示所需的加权平均值。

设置阶段： 每对客户端 $C_i$ 和 $Cj$ 使用 Diffie-Hellman 密钥协商协议建立公共随机数 $r{ij} = r_{ji}$。此共享密钥仅为两个参与客户端所知。所有运算均以某个界限 $p$ 为模执行。

掩码和传输： 在每个训练迭代中，客户端 $C_i$ 使用成对共享随机性屏蔽其权重 $w_i$。具体来说，$Ci$ 添加所有 $j > i$ 的 $r{ij}$，并减去所有 $k < i$ 的 $r_{ki}$，然后发送到服务器：

$\bar{w}_i := \left(wi + \sum{j=i+1}^{n} r{ij} - \sum{k=1}^{i-1} r_{ki}\right) \mod p$

聚合： 服务器从所有客户端接收屏蔽的权重 $\bar{w}_1, \ldots, \bar{w}n$。在对这些值求和时，成对随机性会抵消：每个 $r{ij}$ 都以正项（来自 $C_i$）和负项（来自 $C_j$）的形式出现一次。服务器计算：

$\frac{1}{n}\sum_{i=1}^{n} \bar{w}i = \frac{1}{n}\sum{i=1}^{n} w_i \mod p$

屏蔽值 $\bar{w}_i$ 不会向服务器透露关于各个权重 $w_i$ 的任何信息，因为每个权重都被多个随机项掩盖，而这些随机项仅为成对客户端所知。

添加差分隐私

虽然此协议对服务器隐藏了各个权重，但聚合的输出本身可能会泄漏信息。如果 $n-1$ 个客户端串通，他们可以从聚合中减去他们已知的贡献，以恢复剩余客户端的权重。为了防止这种情况，SMPAI 通过让每个客户端在屏蔽之前向其权重添加校准噪声来合并差分隐私。

在基本方法中，每个客户端独立地从拉普拉斯分布中采样噪声，并将其添加到其本地权重。虽然这提供了基本的安全性，但串通的参与者可以隔离诚实客户端的“嘈杂”权重；这些攻击者可以尝试复制噪声分布（例如拉普拉斯分布）并将其减去以猜测原始敏感输入。但是，SMPAI 引入了一种更强大的机制：分布式噪声生成。客户端不是选择自己的噪声，而是从其他参与者那里接收加密的噪声贡献。每个客户端从其他每个客户端接收两个加密的噪声项，但仅选择两个项中的一个添加到其权重。此选择对于其他方仍然未知。

例如，客户端 $P_1$ 从 $P2$ 接收加密的噪声对 $\bar{\eta}{21} = (\bar{\eta}^0{21}, \bar{\eta}^1{21})$，并从 $P3$ 接收 $\bar{\eta}{31} = (\bar{\eta}^0{31}, \bar{\eta}^1{31})$。客户端 $P1$ 从每对中选择一个项（比如 $\bar{\eta}^1{21}$ 和 $\bar{\eta}^0_{31}$）并计算：

$W_1 = \bar{w}1 + \bar{\eta}^1{21} + \bar{\eta}^0_{31}$

这种分布式机制确保即使当 $n-1$ 方串通时，他们也无法确定诚实方选择了哪些噪声项，与标准本地差分隐私相比，这使得恢复诚实方的原始输入变得更加困难。

安全性与效用的权衡

SMPAI 协议演示了安全联邦学习中的关键权衡。密钥共享机制消除了单点信任，没有中央服务器观察单个贡献。即使在 $n-1$ 方协同工作的情况下，分布式差分隐私也能提供保护。但是，这些安全保证是有代价的：通信开销随参与者的数量呈二次方增加（每对都必须建立共享随机性），并且添加的噪声会降低模型准确性。

使用同态加密的联邦学习

同态加密支持在不解密的情况下对加密数据进行计算，使其非常适合联邦学习中的安全聚合。通过在传输之前对模型更新进行加密，客户端可以保护其梯度免受好奇或受损的聚合器的侵害，同时仍然使服务器能够计算模型平均所需的总和。

BatchCrypt 例示了同态加密集成到跨孤岛设置的联邦学习中：少量组织（每个组织都拥有大量敏感数据集）协同训练模型的场景，该模型只有参与者才能访问。与拥有数百万移动客户端的跨设备联邦学习不同，跨孤岛 FL 通常涉及少于 100 方（例如金融机构、医院或研究组织），这些组织需要强大的隐私保证并且可以容忍更高的计算开销。

BatchCrypt 协议通过以下阶段运行：

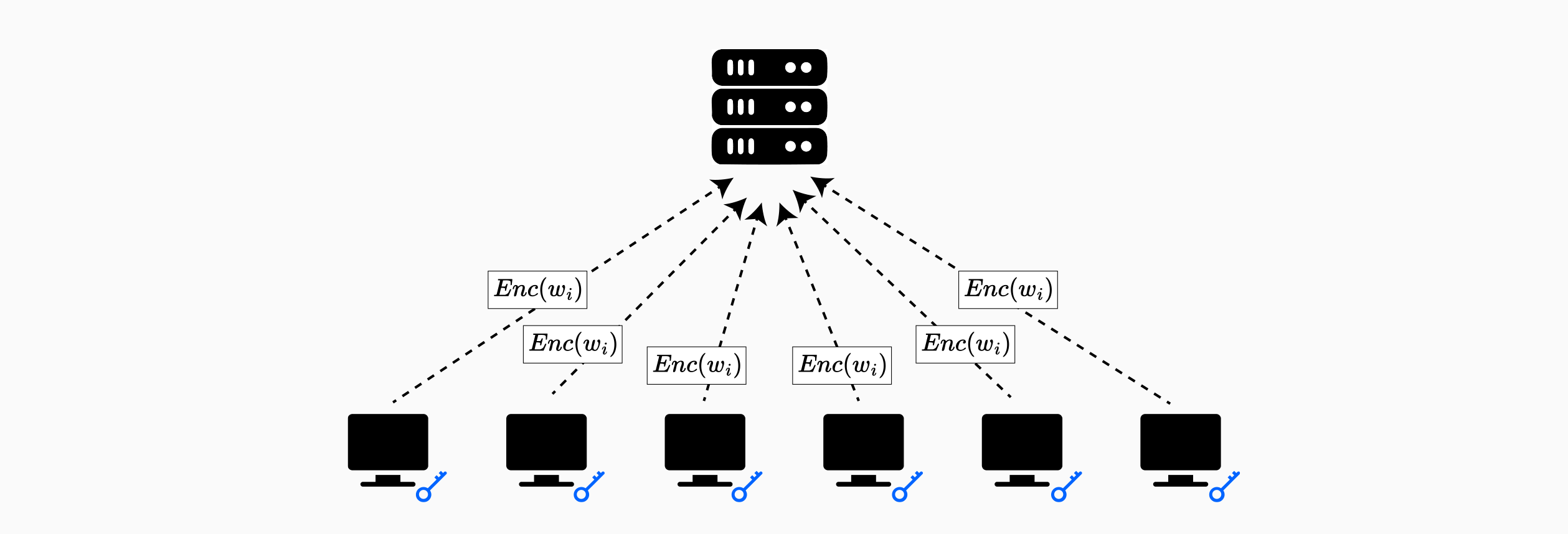
1. 初始化： 在训练开始之前，聚合器随机选择一个参与客户端作为领导者。领导者生成同态加密密钥对并初始化机器学习模型权重。然后，密钥对和初始模型参数都通过安全通信通道安全地传输到所有其他参与客户端。
2. 本地训练和加密： 在每次训练迭代中，每个客户端都使用当前的全局模型计算其本地数据集上的梯度。然后，每个客户端都使用共享公钥加密其梯度向量，并将加密的梯度传输到聚合器。
3. 同态聚合： 聚合器等待直到它收到来自所有参与客户端的加密梯度更新。由于加密方案的加法同态特性，聚合器可以在密文域中直接计算加密梯度的总和，从而生成加密聚合，而无需以明文形式观察各个客户端的贡献。
4. 解密和模型更新： 聚合器将加密聚合返回给所有客户端。每个客户端都独立地使用私钥解密聚合的结果，并将此聚合梯度应用于更新其本地模型副本，然后再进行下一次迭代。

初始化后，BatchCrypt 对所有客户端进行对称处理，在训练期间领导者和其他工作人员之间没有区别。

Paillier 加密和量化

BatchCrypt 采用 Paillier 密码系统，这是一种部分同态加密方案，支持密文上的加法运算。具体来说，给定加密 $Enc(m_1)$ 和 $Enc(m_2)$，Paillier 方案允许计算 $Enc(m_1 + m_2)$ 而无需解密单个消息。此加法属性直接支持梯度聚合运算，该运算是联邦平均的核心。

但是，出现了一个根本性的挑战：神经网络梯度是浮点值，而 Paillier 加密对整数进行运算。为了弥合这一差距，BatchCrypt 采用量化方案，该方案在加密之前将浮点梯度映射到整数表示。

为了进一步优化性能，BatchCrypt 在加密之前将多个量化的梯度编码为单个大整数，从而执行批量加密而不是单独加密每个梯度元素。这种批处理策略大大减少了加密运算的数量以及由此产生的通信开销。

实际限制

尽管 BatchCrypt 架构有效，但它揭示了基于 HE 的联邦学习设计中固有的安全限制。由于所有客户端共享相同的加密密钥对，因此任何单个恶意或受损的参与者都可以解密系统中的所有梯度更新。这种单密钥设计消除了客户端之间的机密性，同时聚合器无法观察各个梯度，客户端本身可以解密并检查彼此的贡献。

此外，即使使用 BatchCrypt 的优化，同态加密运算的计算量仍然很大。HE 运算可能会在联邦学习系统中占据训练时间，从而使该方法主要适用于少数几个强大的组织可以承受计算成本的跨孤岛设置。

这些限制促使人们探索替代的密码学方法，例如安全多方计算和差分隐私，它们在安全保证、计算开销和信任假设之间提供不同的权衡。

用于联邦学习的多方计算

真正的安全多方计算 (MPC) 通过在多个计算方之间分配信任而不是仅用成对随机性屏蔽值来提供比先前讨论的密钥共享方法更强的安全保证。MPC 协议使多个参与方能够在其私有输入上联合计算某个函数，而无需任何参与方了解超出最终输出的任何信息。在联邦学习中，这意味着客户端可以聚合其模型更新，而不会向任何人（包括聚合器）透露单个贡献。

MPCFL 协议例示了使用 Sharemind MPC 框架将 MPC 与联邦学习集成。与客户端既提供输入又执行计算的先前方法不同，MPCFL 引入了清晰的架构分离：输入方（具有训练数据的客户端）和计算方（执行安全聚合的实体）。计算方可以是独立的第三方，也可以是客户端本身的子集，但它们独立于数据贡献过程运行。

这种分离在信任模型中提供了灵活性。组织可以将安全聚合外包给受信任的计算基础设施，而无需暴露其模型更新，或者他们可以将某些客户端指定为计算方，以在联邦内部分配信任。

协议架构

MPCFL 协议通过以下工作流程运行：

本地训练： $N$ 个客户端中的每个客户端都在其私有数据集上训练其本地模型，使用标准联邦学习训练程序（例如，随机梯度下降）计算客户端 $k$ 的权重更新 $W^{(k)}$。

密钥共享： 本地训练后，每个客户端都会生成其权重更新的密钥共享。共享的数量取决于计算方的数量，例如，如果有三个计算方，则每个权重更新都将分为三个加法共享。令 $[[ W^{(k)} ]]$ 表示客户端 $k$ 的密钥共享表示形式，该形式分布在所有计算方之间。

共享分发： 每个客户端向每个计算方发送一个共享。重要的是，没有一个计算方收到完整的权重更新；每个计算方仅持有一个加密密钥共享，该共享不会透露关于原始权重的任何信息。

安全聚合： 计算方联合执行 MPC 协议以聚合共享权重，而无需重建单个客户端的贡献。使用加法密钥共享，它们计算全局聚合权重：

$[[ W^{(global)} ]] = \text{AddFloat}([[ \alpha_1 W^{(1)} ]], \ldots, [[ \alpha_N W^{(N)} ]])$

其中 $\alpha_k$ 表示客户端 $k$ 的权重系数，通常计算为：$\alpha_k = \frac{nk}{\sum{i=1}^{N} n_i}$，其中 $n_k$ 是客户端 $k$ 拥有的训练样本的数量。这确保了具有较大数据集的客户端对全局模型的贡献与它们的训练样本数量成比例。$\text{AddFloat}$ 运算完全在密钥共享上使用 MPC 加法和乘法协议执行，从而生成密钥共享的结果。

结果重建： 聚合后，计算方将其共享的 $[[ W^{(global)} ]]$ 发送回客户端。每个客户端通过组合他们从所有计算方接收的共享来重建全局模型更新。

模型更新： 客户端将重建的全局更新应用于其本地模型，然后进行下一个训练轮。

在整个过程中，单个权重更新受到密钥共享方案的保护。计算方不了解单个贡献，因为它们仅处理密码密钥共享。即使某些计算方受到攻击，只要保持诚实方的阈值数量，安全保证仍然成立（例如，在三方密钥共享中，至少 2 方必须是诚实的）。

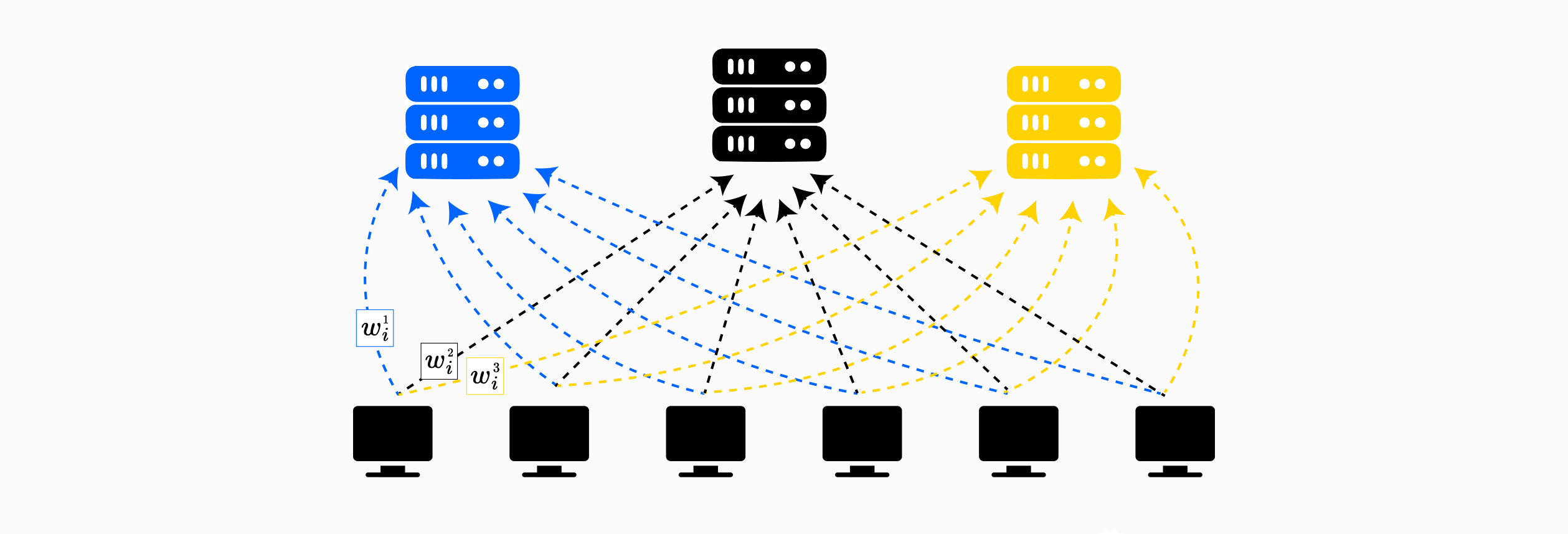
用于联邦学习的多方同态加密

与单密钥 HE 方案相比，多方同态加密 (MHE) 通过在多个方之间分配解密能力，同时保持对加密数据进行计算的能力，代表着一项重大进步。这解决了标准基于 HE 的联邦学习中的一个关键限制：解密能力的中心化。在这篇文章中了解有关 MHE 方案的更多信息。

SPINDLE 协议通过 CKKS 方案的多方自适应例示了 MHE 集成到联邦学习中。与单个方持有密钥的传统同态加密不同，SPINDLE 在所有 $N$ 个数据提供商之间分配密钥，同时维护所有参与者都知道的集体公钥 $pk$。

密钥分发： 每个数据提供商 $DP_i$ 都持有密钥 $sk_i$ 的共享，该密钥通过分布式密钥生成协议 $\text{DKeyGen}({sk_i})$ 生成。关键的安全属性是解密需要所有方的协作，只有在每个数据提供商都参与集体解密协议 $\text{DDec}(\langle v \rangle, {sk_i})$ 时，才能解密在 $pk$ 下加密的密文。

此架构提供 $N-1$ 共谋抵抗：只要一个诚实的数据提供商拒绝参与解密，集体加密的模型仍然是机密的。即使除一个之外的每个参与者都是恶意的并共享其密钥共享，他们也无法解密模型或训练数据。

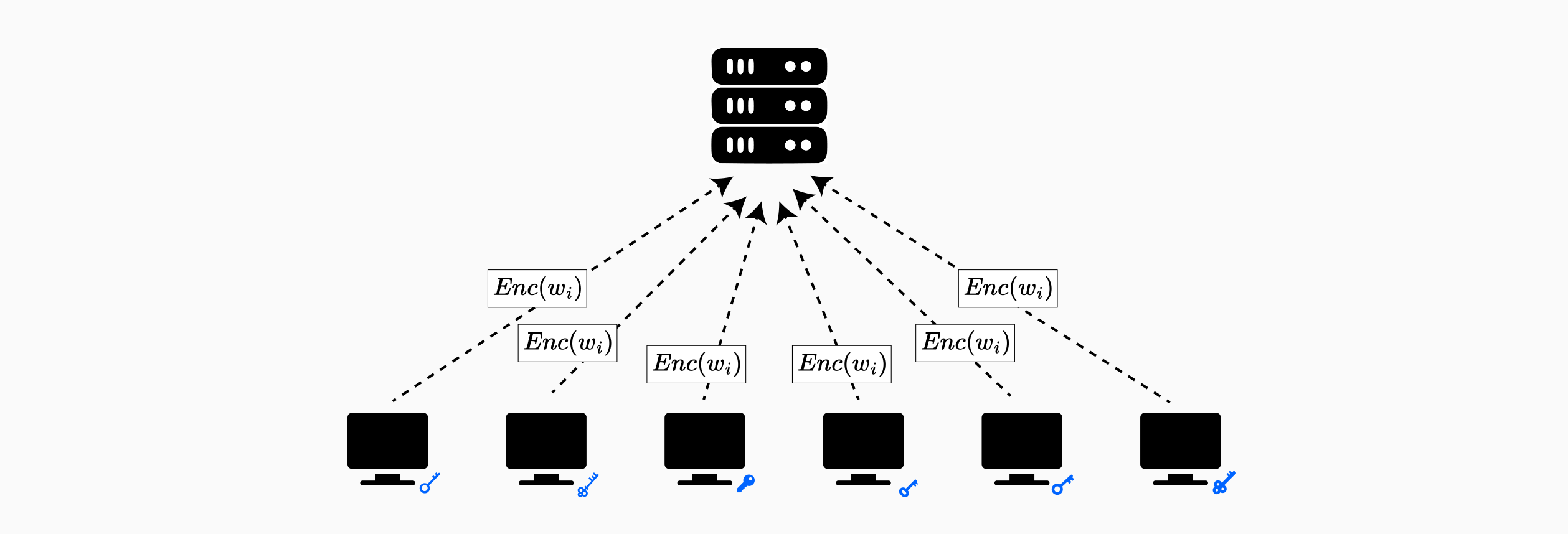
使用加密权重进行训练

SPINDLE 将 MHE 集成到协同随机梯度下降 (CSGD) 训练工作流程中：

初始化： 数据提供商使用 $\text{DKeyGen}$ 共同初始化加密密钥，并在集体公钥 $pk$ 下加密其初始模型权重。

本地训练： 每个数据提供商 $DP_i$ 在其私有数据集 $(X^{(i)}, y^{(i)})$ 上执行 $m$ 次梯度下降本地迭代。

同态聚合（组合）： 加密的本地权重更新 $\langle w^{(i,j)} \rangle$ 在它们上升树结构时使用同态加法进行聚合。每个数据提供商将其加密更新与其子代的加密更新组合，并将结果转发到其父代。根目录的数据提供商获得 $\langle w^{(\cdot,j)} \rangle = \sum_{i=1}^N \langle w^{(i,j)} \rangle$。

全局更新（减少）： 根数据提供商使用加权平均更新加密的全局权重。

在整个过程中，单个权重更新仍然是加密的。任何一方都无法观察到来自其他参与者的明文权重或梯度。

用于私有预测的集体密钥切换

对于预测查询，SPINDLE 使用分布式密钥切换协议 $\text{DKeySwitch}(\langle y' \rangle_{pk}, pk', {sk_i})$，该协议将预测结果从集体公钥集体重新加密到查询者的单个公钥 $pk'$。这确保：

• 查询者可以解密他们的预测结果
• 训练的模型仍然是加密的，并且对查询者隐藏
• 其他数据提供者无法访问预测结果

该协议在推理期间保持模型机密性，同时支持实际的私有预测。

使用零知识证明的可验证联邦学习

到目前为止，探索的密码学机制（同态加密、安全多方计算和差分隐私）解决了数据和模型更新的机密性问题。但是，它们不能保证计算完整性：客户端没有密码学保证聚合器正确执行了商定的聚合算法。恶意或受损的服务器可以选择性地排除某些客户端、注入伪更新或应用不正确的聚合逻辑，同时保持加密通信。零知识证明提供可验证性而不牺牲隐私，从而使客户端能够以加密方式验证正确的聚合，而无需了解单个贡献。

联邦学习聚合中的信任问题

在标准联邦学习中，客户端必须信任聚合器：

1. 在聚合中使用所有提交的更新
2. 应用正确的聚合算法（例如，FedAvg）
3. 不注入虚假客户端或操纵权重

恶意聚合器可能会通过选择性地加权或排除合法的客户端更新来将全局模型偏向特定结果。在参与者具有竞争利益的去中心化或跨组织联邦学习中，这种威胁尤其严重。

zkDFL：使用不受信任的服务器进行可验证的聚合

zkDFL 协议通过与基于区块链的验证集成的零知识证明来解决不受信任的服务器方案。该系统涉及 $K$ 个客户端和一个聚合服务器，其中客户端无法信任服务器能够诚实地聚合。

设置阶段： 每个客户端都使用相同的模型参数进行初始化，并注册一个公共区块链地址。所有客户端都同意聚合算法 (FedAvg) 和将要证明的电路规范。

客户端选择： 在每个训练轮中，服务器从 $K$ 个客户端中选择 $m$ 个客户端参与，从而平衡通信成本和模型质量。选定的客户端在其私有数据集上执行本地训练。

本地训练和提交： 每个选定的客户端 $i$ 都通过在其本地数据集上进行标准随机梯度下降来计算梯度更新 $\Delta w_i$。客户端将梯度更新提交给服务器。

服务器聚合： 服务器接收更新 ${\Delta w_1, \ldots, \Delta w_m}$ 并计算其相应的哈希值 ${H_1, \ldots, H_m}$。它执行 FedAvg 聚合：

$w_{t+1} = wt + \frac{1}{m}\sum{i=1}^m \Delta w_i$

Groth16 零知识证明结构

zkDFL 的关键创新在于使用 Groth16 SNARK 来证明正确的聚合，而无需透露单个更新。服务器为编码 FedAvg 算法的算术电路构建零知识证明。

电路设计： Groth16 电路将以下内容作为输入：

• 私有 witness： 实际的梯度更新 ${\Delta w_1, \ldots, \Delta w_m}$
• 公共输入： 哈希值 ${H_1, \ldots, Hm}$、它们的总和 $\sum{i=1}^m Hi$ 和聚合的结果 $w{t+1}$

该电路同时证明了两个语句：

1. 正确的聚合： 服务器已根据 FedAvg 正确计算了 witness 数据（更新）的算术平均值
2. 哈希一致性： 服务器从同一 witness 数据生成了作为公共数据呈现的确切哈希值

Groth16 证明系统将这些算术约束转换为二次算术程序 (QAP)，并生成简洁的证明 $\pi$。

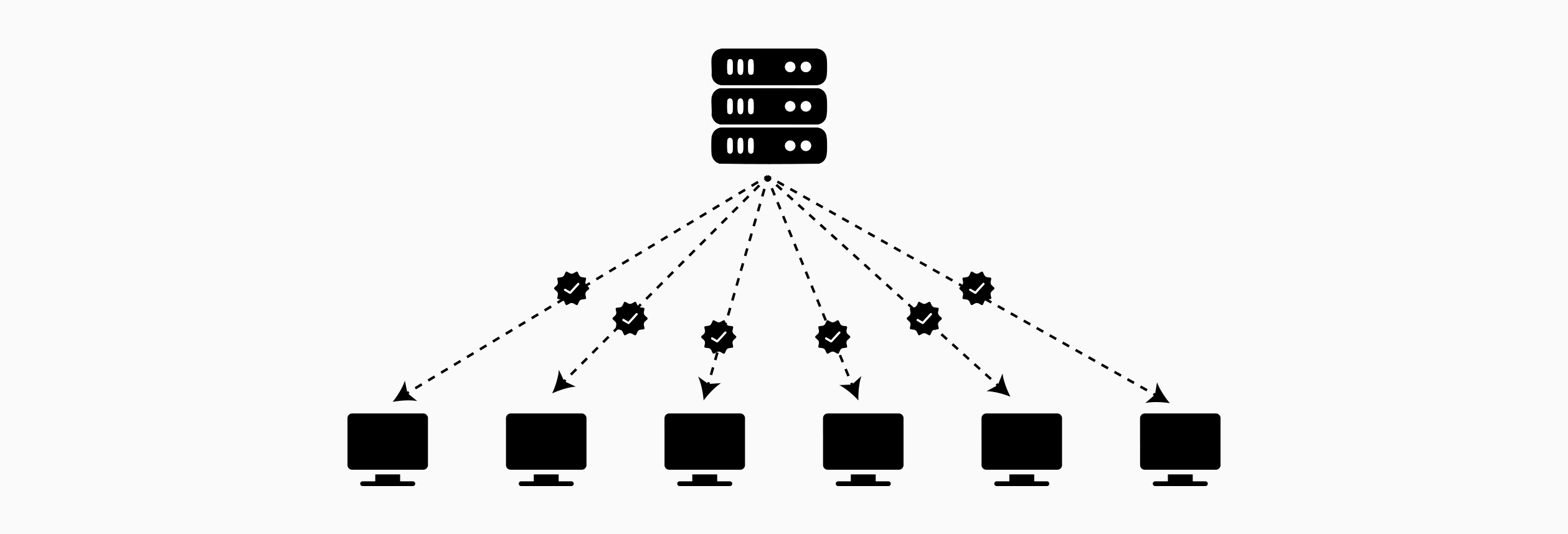
双智能合约验证

zkDFL 采用部署在区块链上的两个互补的智能合约来建立信任：

合约 1 - Groth16 验证器： 此合约验证服务器提交的零知识证明 $\pi$。它检查服务器是否正确聚合了哈希与公共输入匹配的某些更新。但是，仅凭这一点并不能保证服务器使用了来自所有参与客户端的特定更新。

合约 2 - 哈希注册表： 每个客户端都将自己的哈希 $H_i$ 独立地提交到此注册表合约。当第 $m$ 个客户端提交其哈希时，合约会计算：

$H{\text{sum}}^{\text{clients}} = \sum{i=1}^m H_i$

这表示客户端实际提交的哈希值之和。

验证条件： 服务器的证明包括一个公共输出 $H_{\text{sum}}^{\text{server}}$，该输出表示它在聚合中使用的哈希值之和。仅当满足以下条件时，验证才成功：

$H{\text{sum}}^{\text{clients}} = H{\text{sum}}^{\text{server}}$

此等式保证服务器完全使用了来自参与客户端的更新集，没有添加、删除或替换。

具有 不受信任的客户端 的可验证 FL：Federify

虽然 zkDFL 解决了服务器不值得信任的问题，但 Federify 解决了互补的问题：去中心化设置中不受信任的客户端。Federify 不是验证中央服务器是否正确聚合，而是确保客户端在提交本地模型以进行聚合之前正确计算了本地模型。

去中心化架构： Federify 完全消除了中央聚合器，并将其替换为部署在公共区块链上的智能合约。该框架涉及两种类型的参与者：数据所有者 (DO)，他们持有训练数据并参与本地模型更新；以及模型所有者 (MO)，他们通过提供资金和参与阈值解密来赞助训练。

注册阶段： 每个模型所有者通过提交以下内容在智能合约中注册：

• 初始押金（激励诚实的解密参与）
• 本地公钥 $Pk_k$

智能合约聚合所有本地公钥，以形成阈值 ElGamal 加密方案 $P = \sum_{k=1}^{m} P_k$ 的全局公钥。任何一方都可以使用此全局公钥进行加密，但解密需要至少 $m$ 个模型所有者中的 $t$ 个进行协作。

阈值密钥管理

Federify 的安全性依赖于通过 $(t,m)$-阈值 ElGamal 密码系统在多个方之间分配解密能力。每个模型所有者 $MO_k$ 都生成一个密钥 $sk_k$ 和相应的公钥 $P_k = sk_k G$（其中 $G$ 是椭圆曲线上的基点）。私钥永远不由一个人持有；相反，每个 MO 都使用多项式密钥共享来共享他们的密钥。阈值属性确保必须至少有 $t$ 个模型所有者参与才能进行解密，从而防止任何单方或少数联盟访问明文模型。

可验证的本地训练

数据所有者在其本地数据上训练高斯朴素贝叶斯分类器。对于一批具有 $f$ 个特征的 $\beta$ 个样本，DO 计算每个特征 $i$ 的均值 $\mu_i$ 和方差 $\sigma_i^2$。在提交之前，DO 会加密这些参数：

$S=\{(\mu_i, \sigma^2i)\}{i=1}^f \text{ 其中 } \mu_i = E_P(\mu_i, r_i), \quad \sigma^2_i = E_P(\sigma^2_i, r'_i)$

关键的验证步骤使用两个 zkSNARK 电路：

电路 1 - ValidateModel： 验证模型参数是否从训练数据中正确计算

电路 2 - ValidateEncryption： 验证加密是否使用了正确的全局公钥 $P$

数据所有者向智能合约提交交易 $Tx(\text{Proof}, S, P)$，该合约验证证明，然后接受更新。验证后，智能合约会同态地聚合加密的参数。 此聚合利用 ElGamal 的加法同态属性：$E(m_1 + m_2) = E(m_1) \cdot E(m_2)$。

具有验证的阈值解密

一旦 $p$ 个数据所有者提交了所有类的更新，模型所有者就会协同解密聚合的模型。每个 $MOk$ 使用自己的密钥共享 $C{sk_k} = C - sk_k R$ 执行部分解密，其中 $(R, C)$ 表示加密的聚合参数。为了防止恶意的 MO 提交不正确的部分解密，每个 MO 都必须提供 zkSNARK 证明 (ValidateDecryption)，以证明：

$P_k = skk G \wedge C{sk_k} = C - sk_k R$

智能合约验证每个部分解密证明。一旦提交了 $t$ 个有效的局部解密，就可以恢复明文全局模型：

$m = C - \sum_{k=1}^t sk_k R$

阈值属性确保了鲁棒性：即使某些 MO 拒绝参与，任何 $t$ 个诚实的 MO 都可以使用他们的密钥共享来恢复丢失的贡献。

结论

联邦学习 支持协同模型训练，而无需集中处理敏感数据，但简单的实现仍然容易受到隐私和完整性攻击。本文探讨了解决三个关键要求的密码学机制：模型更新的机密性、针对恶意参与者的鲁棒性以及计算的可验证性。

密钥共享和同态加密在聚合期间提供机密性，并在计算开销和安全保证之间进行权衡。多方计算在多个方之间分配信任，从而消除了单点故障。差分隐私通过校准的噪声添加正式的隐私保证，从而以准确性换取针对推理攻击的保护。零知识证明支持可验证的计算，从而使参与者能够以加密方式验证正确的聚合或本地训练，而不会损害隐私。

这些方法之间的选择取决于部署环境。拥有数百万客户端的跨设备联邦学习需要轻量级协议，而强大机构之间的跨孤岛设置可以容忍更繁重的加密运算。去中心化架构受益于基于区块链的验证。 这些密码学机制不仅仅是理论上的构造，它们已经从学术研究过渡到生产部署。现在有几个框架提供了安全联邦学习技术的实现。NVIDIA FLARE 为医疗保健和金融应用提供同态加密和差分隐私功能。TensorFlow Federated 将安全聚合协议集成到 Google 的机器学习生态系统中。Flower 提供了一个框架无关的平台，支持通过掩蔽实现差分隐私和安全聚合。FATE 实现了多种密码学协议，包括同态加密和安全多方计算，用于企业联邦学习。这些可用于生产的框架表明，安全联邦学习已经超越了概念验证，医疗保健、金融和技术领域的组织正在积极大规模地部署保护隐私的协作机器学习系统。

• 原文链接： hexens.io/blog/secure-fl...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～