Zig 签名(Ed25519 和 ECDSA)
- asecuritysite
- 发布于 2026-01-07 10:21
- 阅读 1227
本文介绍了在 Zig 编程语言中使用 Ed25519 和 ECDSA 实现数字签名的方法。通过 Zig 语言,开发者可以在嵌入式系统中高效地进行签名生成和验证,确保数据的完整性和真实性。文章分别提供了 Ed25519 和 ECDSA 的原理概述、代码示例和运行结果,展示了如何在 Zig 中使用这两种签名算法。

Zig 签名 (Ed25519 和 ECDSA)
数字信任的核心是数字签名。有了它,我们创建一个密钥对(一个秘密/私钥和一个公钥),然后用私钥对消息的哈希进行签名,然后用相关的公钥验证签名。
目前使用的三种主要经典签名方法是 RSA、ECDSA 和 EdDSA。每一种都有其自身的优点和缺点,但通常由于 ECDSA 和 EdDSA 相对较小的密钥大小和签名,因此在许多用例中更受欢迎,并且它们在密钥对生成以及签名和验证方面通常具有良好的性能水平。
对于 EdDSA(例如 Ed25519),我们有一个确定性签名(对于相同的私钥和消息,它不会更改),而对于 ECDSA(例如 P256 曲线),我们有一个非确定性签名(每次都使用一个 nonce 值来更改签名 — 即使我们使用相同的消息和私钥)。
因此,许多编程语言都支持 ECDSA 和 EdDSA 签名的实现,但对于嵌入式系统来说,最好的方法之一是使用 Zig 编程语言。
Zig 和 Ed25519
使用 Ed25519,Alice 将使用她的私钥对消息进行签名,然后 Bob 将使用她的公钥来验证她是否对消息进行了签名(以及消息现在是否已更改):
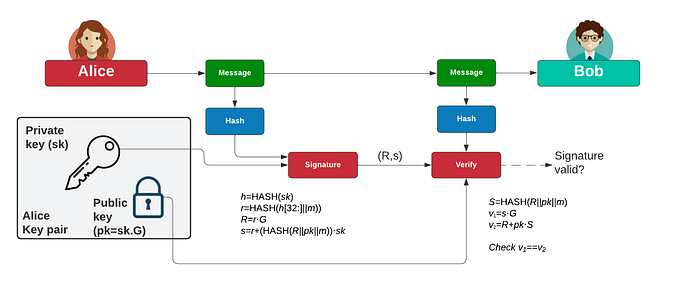
最初,Alice 生成一个随机的 32 字节的密钥 (sk),然后创建一个公钥:
pk = sk ⋅ G, 其中 G 是曲线的基点。Alice 创建她的私钥的 SHA-512 哈希:
h =HASH( sk)
从哈希的上 32 个字节和消息创建 r:
r =HASH( h[32:]|| m))
其中“||”表示字节数组值的连接。接下来,她将 r 匹配到曲线上:
R = r ⋅ G
接下来,Alice 计算 s:
s = r +(HASH( R || pk || m))⋅ sk
签名是 (R, s)。R 和 s 的值均为 32 字节长,因此签名长度为 64 字节。为了验证,Bob 使用 R、pk 和 m 创建 S:
S =HASH( R || pk || m)
接下来创建两个验证值:
v 1= s ⋅ G
v 2= R + pk ⋅ S
如果 v 1== v 2,则签名检查通过。这是因为:
v 1= s. G =( r +(HASH( R || pk || m))⋅ sk)⋅ G = rG + sk ⋅ G ⋅(HASH( R || pk || m))= R + pk ⋅ S = v 2
以下代码使用 Zig 版本 0.15.1 编译 [ 在这里]。使用 Zig,我们可以使用 Ed25519 来对消息进行签名和验证 [ 在这里]:
const std = @import("std");
const crypto = @import("std").crypto;
const Ed25519 = crypto.sign.Ed25519;
pub fn main() !void {
var stdout_buffer: [4096]u8 = undefined;
var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
const stdout = &stdout_writer.interface;
// Get the command-line arguments
// 获取命令行参数
var message: []u8 = undefined;
const args = try std.process.argsAlloc(std.heap.page_allocator);
defer std.process.argsFree(std.heap.page_allocator, args);
// Check if there are any arguments
// 检查是否有任何参数
if (args.len > 1) {
message = args[1];
}
try stdout.print("Message: {s}\n", .{message});
// Key Generation
// 密钥生成
const key_pair = Ed25519.KeyPair.generate();
const public_key = key_pair.public_key; // Share this public key
// 共享此公钥
// Signing
// 签名
const signature = try key_pair.sign(message, null); // Deterministic signature
// 确定性签名
// Verify with the public key
// 使用公钥验证
try stdout.print("\nKey pair (secret): {x}\n", .{key_pair.secret_key.bytes});
try stdout.print("\nKey pair (public): {x}\n", .{key_pair.public_key.bytes});
try stdout.print("\nEd25519 signature (r): {x}\n", .{signature.r});
try stdout.print("\nEd25519 signature (s): {x}\n", .{signature.s});
var rtn = signature.verify(message, public_key);
try stdout.print("\nSignature verification. Rtn: {!}\n", .{rtn});
const incorrect_message = "Wrong message!";
rtn = signature.verify(incorrect_message, public_key);
try stdout.print("\nSignature verification (with wrong message). Rtn: {!}\n", .{rtn});
try stdout.flush();
}一个示例运行是 [ 在这里]:
Message: Hello
Key pair (secret): 5ed1ae8debf5f41cfe30b3df47090804b0f189eee8d1538e312f6f6aff0aa32b0f2ad2b0f40cdea3577e8f287bc306a67d44c1dcbf47555744f01210d57fd64f
Key pair (public): 0f2ad2b0f40cdea3577e8f287bc306a67d44c1dcbf47555744f01210d57fd64f
Ed25519 signature (r): d91df11c51c617cc359e6c48fd2185b24ceddf58f3de94fc0b79a6a07b537695
Ed25519 signature (s): aab17214103198dee29c2f8730019fe32392d8e140bae8c1fe170c462b9ad30a
Signature verification. Rtn: void
Signature verification (with wrong message). Rtn: error.SignatureVerificationFailedZig 和 ECDSA
ECDSA 的概述如下:
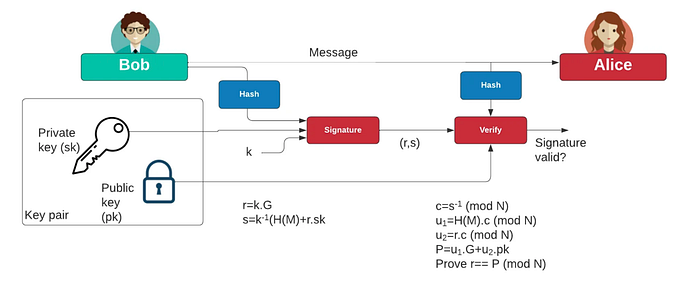
对于我们的曲线,我们有一个生成器点 G 和一个阶 n。我们首先生成一个私钥 (d),然后生成公钥:
Q = d. G
公钥是曲线上的一个点,它是由将点 G 加 d 次得出的。
对于一条消息 (m),我们的目标是应用私钥,然后创建一个签名 (r, s)。首先我们创建一个随机 nonce 值 (k),然后确定该点:
P = k. G
接下来我们计算这个点的 x 轴点:
r = Px(mod n)
这给了我们签名的 r 值。接下来,我们获取消息的哈希值:
e = H( m)
然后计算 s 值:
s = k −1.( e + d. r)(mod n)
我们可以通过获取消息 (m)、签名 (r, s) 和公钥 (Q) 来进行验证:
e = H( m)
接下来我们计算:
w = s ^{−1} (mod n)
u 1= e. w
u 2= r. w
然后我们计算该点:
X = u 1. G + u 2. Q
然后取 X 的 x 坐标:
x = X_x(mod n)
如果 x 等于 r,则签名已验证。
以下代码使用 Zig 版本 0.15.1 编译 [ 在这里]。使用 Zig,我们可以使用 ECDSA 来对消息进行签名和验证 [ 在这里]:
const std = @import("std");
const crypto = @import("std").crypto;
const ECDSA = crypto.sign.ecdsa;
pub fn main() !void {
var stdout_buffer: [4096]u8 = undefined;
var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
const stdout = &stdout_writer.interface;
// Get the command-line arguments
// 获取命令行参数
var message: []u8 = undefined;
const args = try std.process.argsAlloc(std.heap.page_allocator);
defer std.process.argsFree(std.heap.page_allocator, args);
// Check if there are any arguments
// 检查是否有任何参数
if (args.len > 1) {
message = args[1];
}
try stdout.print("Message: {s}\n", .{message});
// Key Generation
// 密钥生成
const key_pair = ECDSA.EcdsaP256Sha256.KeyPair.generate();
const public_key = key_pair.public_key; // Share this public key
// 共享此公钥
// Signing
// 签名
const signature = try key_pair.sign(message, null); // Deterministic signature
// 确定性签名
// Verify with the public key
// 使用公钥验证
try stdout.print("\nKey pair (secret): {x}\n", .{key_pair.secret_key.bytes});
try stdout.print("\nKey pair (public) - compress: {x}\n", .{key_pair.public_key.toCompressedSec1()});
try stdout.print("\nKey pair (public) - Non-compress: {x}\n", .{key_pair.public_key.toUncompressedSec1()});
try stdout.print("\nECDSA P256 signature (r): {x}\n", .{signature.r});
try stdout.print("\nECDSA P256 signature (s): {x}\n", .{signature.s});
var rtn = signature.verify(message, public_key);
try stdout.print("\nSignature verification. Rtn: {!}\n", .{rtn});
const incorrect_message = "Wrong message!";
rtn = signature.verify(incorrect_message, public_key);
try stdout.print("\nSignature verification (with wrong message). Rtn: {!}\n", .{rtn});
try stdout.flush();
}一个示例运行是 [ 在这里]:
Message: Hello
Key pair (secret): 6ce6ea5c6c3ffd7328c3b5fa3dc729abc2532bf9bdf08073c203d416329cad7f
Key pair (public) - compress: 03cac1f2dfeca0890ef9ae2a39f43a6afedae6c16e99b549d4e583003e220ef631
Key pair (public) - Non-compress: 04cac1f2dfeca0890ef9ae2a39f43a6afedae6c16e99b549d4e583003e220ef6312f95b7f087cd11d6e63da2b6c32698fc66eeae689adad7d35dd04a800477513b
ECDSA P256 signature (r): 39cddcda61218a862bc1464c870c798ff1545ac2918c61dbf3abe1a8c4ea8bd5
ECDSA P256 signature (s): 6b674441649df03766cf420196def4795de818818033dd7ed38be09fe902e3f6
Signature verification. Rtn: void
Signature verification (with wrong message). Rtn: error.SignatureVerificationFailed我们可以选择压缩公钥(以 0x2 或 0x03 开头,后跟 x 轴点)或未压缩点(以 0x04 开头,然后是公钥点的 x 和 y 坐标)。在本例中,我们使用了带有 SHA-256 哈希的 P256 曲线 (ECDSA.EcdsaP256Sha256.KeyPair.generate();)。我们可以使用的其他选项有:
EcdsaP256SSha3_256 (适用于使用 SHA-3 256 的 P256)
EcdsaP384Sha3_384 (适用于使用 SHA-3 384 的 P384)
EcdsaP384Sha384 (适用于使用 SHA-384 的 P384)
EcdsaSecp256k1Sha256 (比特币曲线)如果我们需要与比特币和以太坊集成,我们通常会使用 secp256k1 曲线。
如果你想了解有关 Zig 的更多信息,请访问此处:
https://asecuritysite.com/zig/
- 原文链接: medium.com/asecuritysite...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 以太坊协议研究学习小组 - 2026 启动 228 浏览
- 神奇的 Zig、C 和 OpenSSL 187 浏览
- 以太坊签名方案解析:ECDSA、BLS、XMSS 以及带 Rust 代码示例的后量子 leanSig 329 浏览
- 配对密码学之美:聚合签名和阈值签名 300 浏览
- 配对密码之美:聚合签名和阈值签名 501 浏览
- Shamir份额的魔力:BLS门限签名 456 浏览
- 论“高保证”密码学的承诺 301 浏览
- zkMesh:2026年1月回顾 445 浏览
- Solana安全检查清单:Anchor和原生程序的45个关键检查项 447 浏览
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 422 浏览
- 量子计算与区块链:匹配紧迫性与实际威胁 1086 浏览
- ZK 编年史:电路(第二部分) 418 浏览

