从Pedersen承诺的范围证明中移除配对、Bulletproofs或零知识证明 - 密码学

摘要

简化的范围证明。只需要 6 个 ECMUL 和 3 个 ECADD (37K gas) 即可在 EVM 上验证基于 Pedersen 承诺的隐私币的范围证明。第一次设置和承诺需要 zkSNARKs，但之后成本会降至最低。对于客户端的每个交易生成，也不需要 ZKP 计算。

包含安全证明的完整论文：https://eprint.iacr.org/2025/1811.pdf

步骤：

G, H, B 是曲线上的独立点。

每个证明者（token 发送者）的一次性设置

1. 采样 a ← Zq 并设置公共锚点 U = aB。
2. 使用曲线上的点创建一个 Merkle 树。对于每个 X ∈ {1, . . . , 2 n}，定义叶子有效负载 aXG
3. 通过链上的 NIZK，证明由 aXG 组成的树的 Merkle 根。（pre-range proof）

\ Untitled presentation (11)960×540 20.3 KB

证明（发送 token 时）

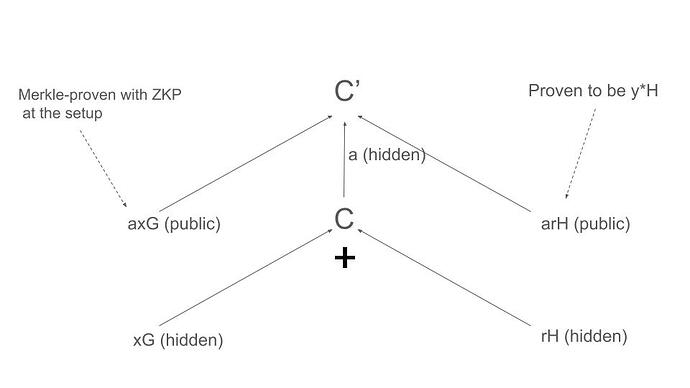
1. 使用 token 数量 x 和隐藏 r 生成 Pedersen 承诺 C = xG + rH。（x、r、xG 和 rH 不应暴露）
2. 提交 C, C’ = aC, axG 及其 Merkle 证明，(U, B) 和 (C’, C) 的 Chaum-Pedersen DLEQ 证明，arH 和 Schnorr 协议的 (arH, H) 证明

验证（C 是否在 EVM 上的某个范围内）

1. 使用 Chaum-Pedersen DLEQ 检查 (U, B) 和 (C’, C) 是否具有相同的离散值

2. 使用 Schnorr 协议或 ECDSA 检查证明者是否可以从 H 生成 arH。

3. 检查设置树中 axG 的 Merkle 证明。

4. 检查 C’ = axG + arH

## 为什么需要 Chaum-Pedersen DLEQ 和 U=aB

如果我们使用 Schnorr 协议或 ECDSA 检查 (C’, C) 的关系，恶意证明者可以生成 C’ = yC 和 C = (bigX)G + rH，其中 y = ax/(bigX)。yrH 也将被验证。

如何缩小树的尺寸

使用带有 nonce 的所有金额数字制作树会有点挑战性。通过有限的随机数制作点树，并将叶子乘以标量并在链上添加一个点会有很大帮助，因为没有人可以从树中曲线上的点猜出随机数。

• 原文链接： ethresear.ch/t/removing-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～