GKR 教程 - 加速零知识证明的密码学方案 - Vitalik

GKR 教程

特别感谢 Lev Soukhanov、Zhenfei Zhang、Zachary Williamson 和 Justin Drake 提供的反馈和审查

如果你正在关注“加密货币的密码学方面”，那么此时你可能已经听说了很多关于超快速 ZK-prover 的信息：ZK-EVM Prover 实时证明以太坊 L1，仅使用大约五十个消费级 GPU，人们 证明 在消费级笔记本电脑上每秒进行 200 万次 [Poseidon 哈希运算]，以及 zk-ML 系统证明 LLM 推理，速度不断提高。

在这篇文章中，我将详细解释一类协议，这些协议是许多这些证明系统实现极端速度的幕后功臣：GKR。

我将重点介绍 GKR 在证明 Poseidon 哈希（以及其他遵循类似模式的计算）方面的实现。要在更通用的电路评估的背景下了解 GKR，请参阅 Justin Thaler 的笔记 和 这篇 Lambdaclass 文章。

什么是 GKR，为什么它这么快？

假设你有一个在两个维度上都很“大”的计算：它涉及通过至少中等数量的（低阶）“层”处理数据，并且它涉及将相同的函数应用于大量的输入。如下图所示：

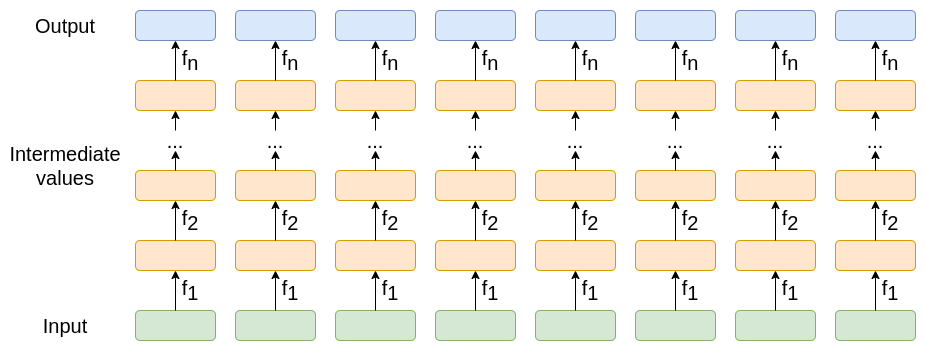
事实证明，我们所做的大量最大规模的计算都符合这种模式。密码学家会注意到，许多计算密集型的证明操作都涉及证明大量的哈希，并且每个哈希内部都具有完全相同的内部结构。AI 研究人员会注意到，神经网络（LLM 的核心构建块）具有完全相同的内部结构（既因为你可以并行证明许多 token 的推理，又因为在每个 token 内部，你都有一个混合元素级神经层和全局矩阵乘法层的结构，这在技术上违反了上图中跨输入的独立性，但在实践中很容易放入 GKR 系统）。

GKR 是一种专门为这种模式量身定制的密码学方案。它通过避免需要对任何中间层进行 承诺(make commitments) 来实现其效率：你只需要对输入和输出进行承诺。“承诺”在这里指的是将数据放入密码学数据结构中，无论是 KZG 还是 Merkle 树，这使你可以证明有关该数据的特定内容的查询。最便宜的承诺，即纠删码的 Merkle 树（在 STARK 中使用），需要你为每个你承诺的字节哈希 4-16 个字节：数百个加法和乘法，而你在此步骤中证明的底层操作可能只是一个乘法。GKR 避免了所有这些，除了在最开始和最后。

请注意，GKR 不是“零知识的”：它只处理简洁性，不处理隐私。如果你想要零知识，请将 GKR 证明包装在 ZK-SNARK 或 ZK-STARK 中。

Sumcheck：核心构建块

假设你有一个多元多项式 P(x1,x2...xN)，它在每个维度上都是低阶的。你想证明该多项式在超立方体上的求值之和 — 也就是说，你想证明 ∑ik∈{0,1}P(i1,i2...iN) 的值。有一种标准技术可以将这个问题简化为在随机坐标处计算 P 的问题。也就是说，你可以将证明 ∑ik∈{0,1}P(i1,i2...iN) 的“义务”转换为证明 P(c1,c2...cN) 的义务，其中 c1,c2...cN 是在证明过程中随机生成的。以下是对于多线性多项式（在每个变量中都是线性的；因此允许 xixj，但不允许例如 xi2）的情况：

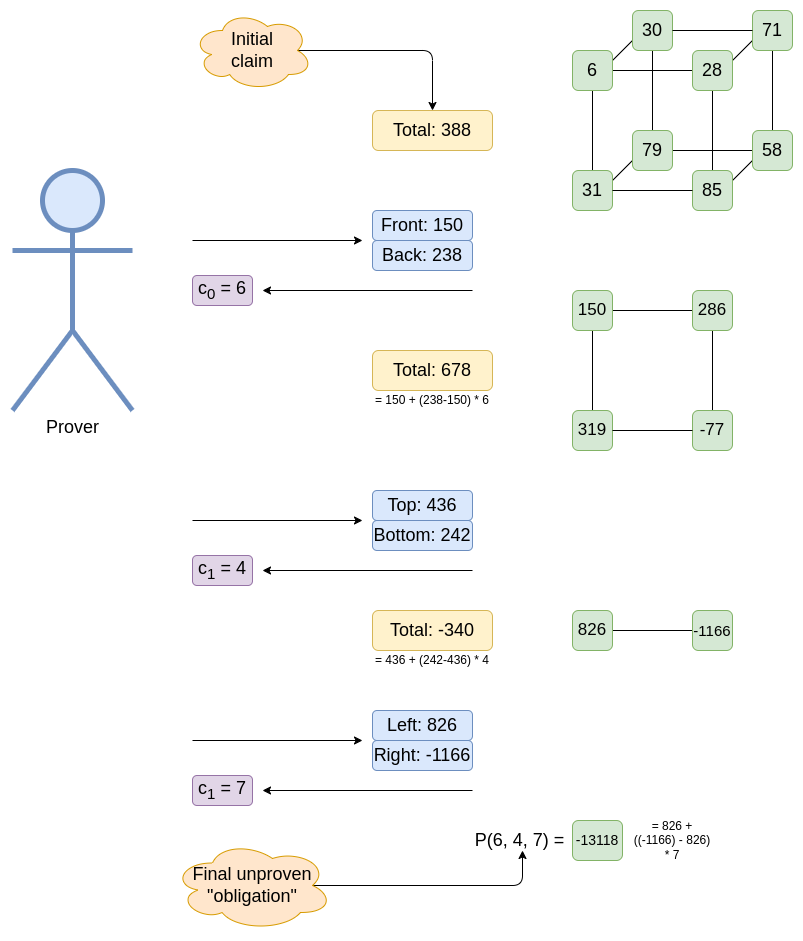
在每一步中，prover 都会为当前超立方体的每个一半提供一个总和。这些总和（和任何先前的随机性）会被哈希在一起，并用作选择评估坐标的随机性。然后，prover 使用超立方体两个一半的简单线性组合（维度 N）来计算评估的半尺寸（维度 N-1）超立方体，其中第一个坐标设置为刚刚随机选择的评估坐标。在上图中，prover 从在 ((0,0,0), (0,0,1) ... (1,1,1)) 处的评估开始，并将上半部分加上 6 乘以其与下半部分之间的差来计算在 ((6,0,0), (6,0,1), (6,1,0), (6,1,1)) 处的评估的半尺寸超立方体。

这是一个标准的“随机线性组合”技巧：通过证明线性声明（在本例中为总和）对于这些值的随机线性组合是正确的，来证明该声明（在本例中为超立方体的两个一半）对于多个值（此处）是正确的。在 bulletproof 中也使用了类似的想法。并且像在 bulletproofs 中一样，我们递归地使用随机线性组合技巧：prover 继续将关于超立方体的声明转换为关于一半大小的超立方体的声明，直到“超立方体”缩小为一个单一值。该值是原始多元多项式在随机点（此处为 (6, 4, 7)）处的评估。如果 prover 可以证明该评估，那么他们就证明了原始总和。

sumcheck 本身没有用：毕竟，它只是将关于一堆数字的一个未经验证的声明转换为关于一堆数字的另一个未经验证的声明。但它是包括 GKR 在内的一大堆证明系统中一个非常有用且功能强大的要素。它也非常高效：特别是，prover 不需要承诺任何东西，并且 prover 和 verifier 每个回合只需要哈希一小部分常量数据即可生成随机坐标。

现在，让我们进入 GKR。对于这篇文章，我们将重点关注一种计算：证明大量 Poseidon2 哈希函数的哈希值。Poseidon2 哈希函数非常简单；这是一个对其使用的核心置换函数的完整图形描述：

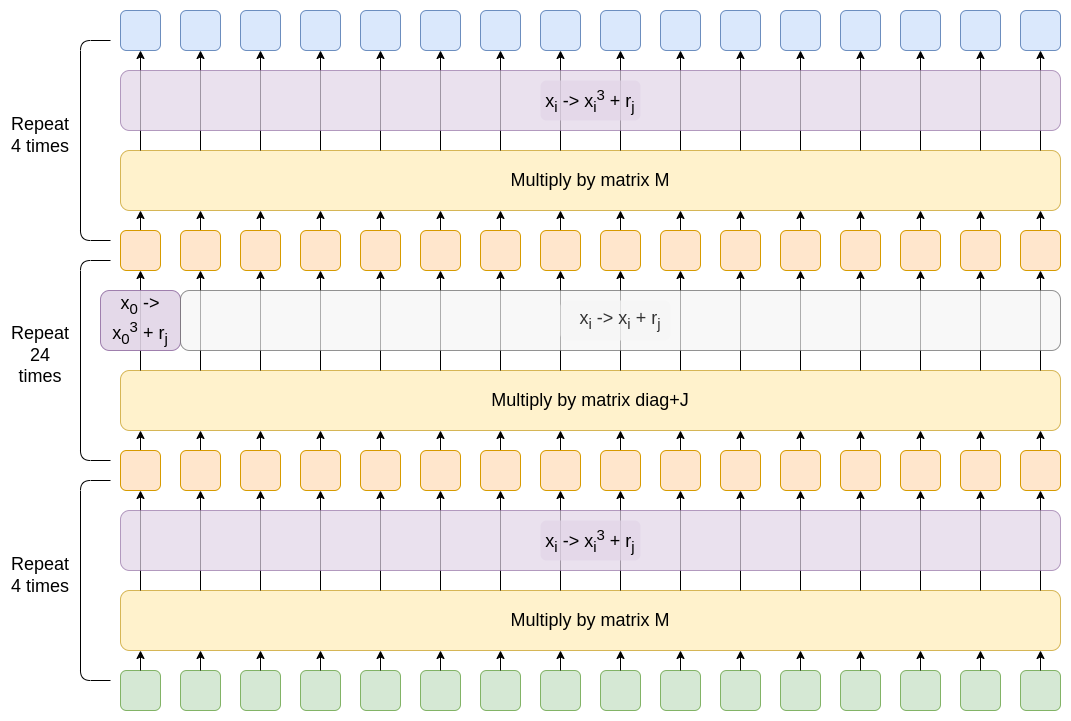
本质上，你进行许多轮交替的操作，包括将整个数据乘以一个矩阵，以及将每个元素立方并加上一个常数。中间的回合是“部分回合”，其中两个操作都被简化：矩阵是一个“简单”的矩阵（上图中的 diag+J），可以评估为 xi→xi∗di+sum(x0,x1...x15)，并且只有第一个值被立方。这种完整回合和部分回合的组合被认为是性能和安全性之间权衡的最佳选择，但这对于构造而言并非必不可少：如果你愿意，你可以只使用具有随机矩阵的完整回合。

Poseidon2 有许多版本和参数选择；以上并非旨在准确描述任何特定的实时实现，而是显示了一般模式。

GKR 非常适合并行证明大量这样的执行。让我们来看看它是如何工作的。我们将首先从一个简化的 Poseidon 版本开始，其中没有部分回合和没有矩阵 - 相反，你只需重复执行 x→x3+rj。GKR 通过向后运行计算来工作：

• 首先，prover 从证明最终输出的“义务”开始。
• 我们将输出视为超立方体上多元多项式的评估，我们要求 prover 通过证明在该随机选择的点处评估的此“输出多项式”来证明输出。
• 从那里，我们反复使用 sumcheck 逐步将此“义务”转换为证明关于前一层的声明的义务。
• 最终，我们得到证明表示输入的多元多项式评估的义务。verifier 知道输入，因此他们可以直接检查。

这是顶层。为了更清晰的表述（即，为了避免数字的大小爆炸），在此示例中，我们将对所有数学模 89 进行运算。实际上，V 是 Poseidon 计算的输出，因此它是 32 位素数域中的数字（通常是 KoalaBear (231−224+1)），并且 pi（因此在本文章后面的 W）是在 4 次扩展域上的（通常表示为 x=a0+a1v+a2v2+a3v3 形式的元素，其中 v4=3）以确保（接近）128 位安全性。

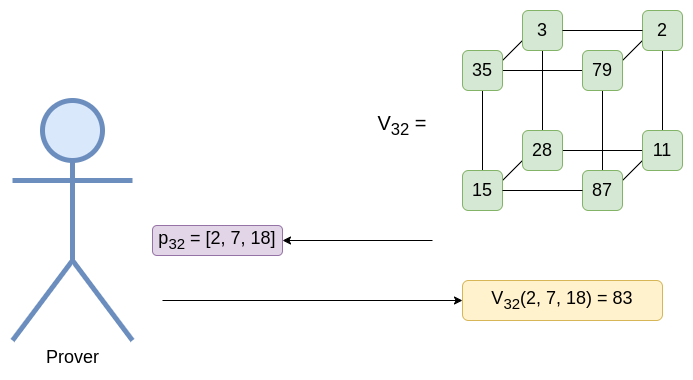
请注意，我们尚未进行任何 sumcheck。我们所做的第一个 sumcheck 实际上将在倒数第二层（即 V31）上。为此，我们需要引入一些额外的机制。特别是，目标不是证明基本和 ∑ik∈{0,1}V31(i1,i2...iN)。相反，我们正在证明 ∑ik∈{0,1}(V31(i1,i2...iN)3+r31)∗W31(i1,i2...iN)。

此处的 W31 是与“在 p32 处评估”相对应的“权重”。多线性多项式的任何评估都可以由权重表示。例如，考虑具有评估 [[1, 5], [3, 9]] 的 2D 多线性多项式：

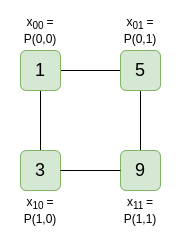
现在，假设我们想要在 (4, 6) 处进行评估。我们可以计算它！一种简单的方法是沿着水平或垂直线取差值（例如 x01−x00），并一遍又一遍地重新应用它以“扩展”该线：

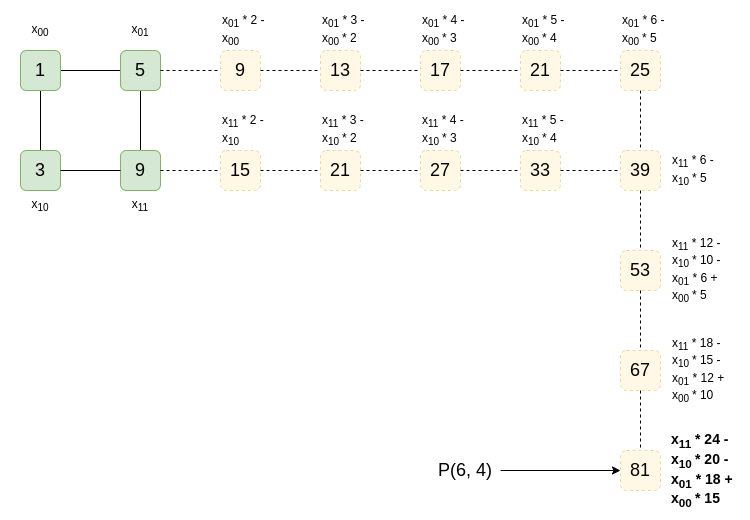
这里，[[15, -18], [-20, 24]] 是对应于“在 (4, 6) 处评估”的“权重”。我们也可以通过一个很好的公式来计算权重：[[(1−4)∗(1−6),(1−4)∗6],[4∗(1−6),4∗6]]。类似的事情也适用于更高的维度。

回到 GKR。我们想要证明其值的表达式为 ∑ik∈{0,1}(V31(i1,i2...iN)3+r31)∗W31(i1,i2...iN)。因为 W31 是对应于“在 p31 处评估”的权重，所以此表达式与说“计算 (V31(i1,i2...iN)3+r31)(p31)”完全相同，这本身与 V32(p31) 相同。现在，我们进行 sumcheck。它与我们之前所做的类似，只是在每一步中，我们提供的不是值的本身的部分和，而是值的评估。此外，还有另一个细微差别：因为这是一个 4 阶表达式（来自 V313 的 3 阶和来自 W 的 1 阶），我们需要在每一步提供五个评估，而不仅仅是左侧和右侧。

这一切都很复杂，所以为了避免增加更多的痛苦，让我们将 r31 设置为零，这样我们就可以专注于立方。我们开始吧：

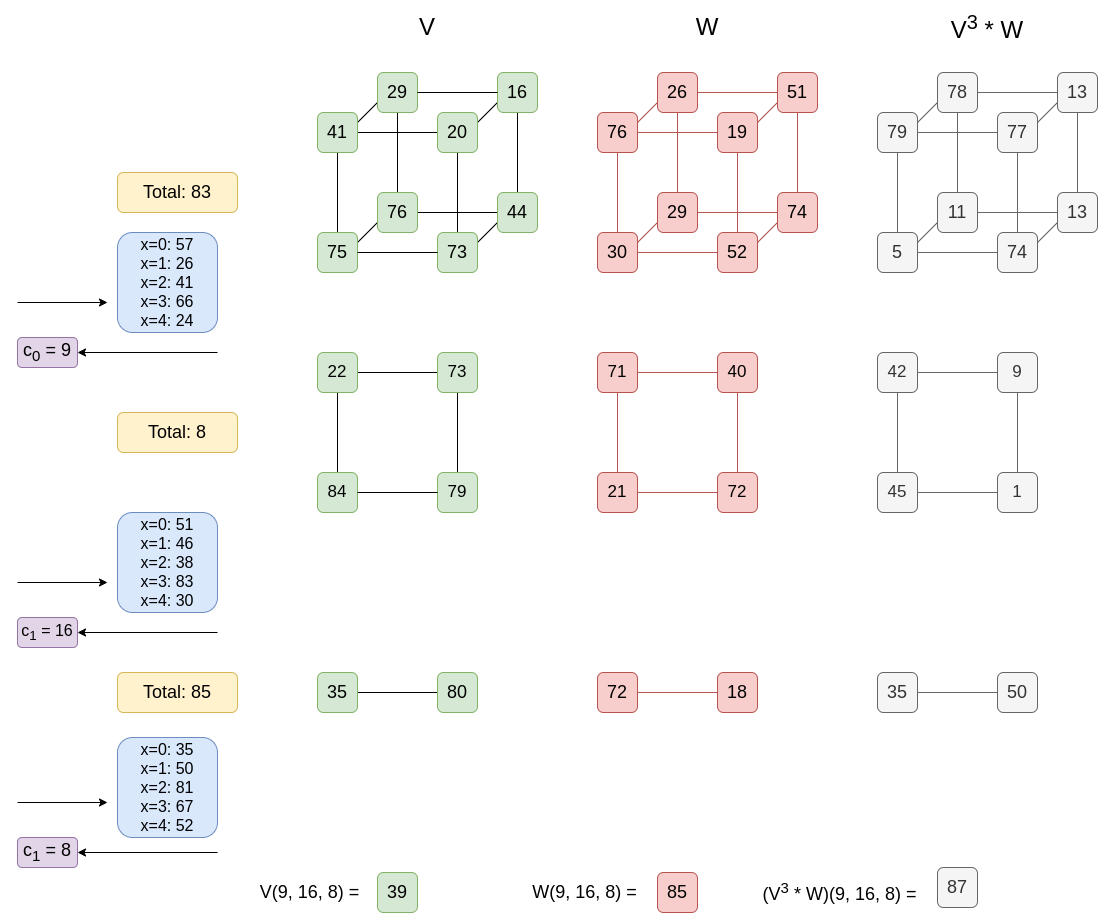
正如机器人喜欢说的那样，让我们逐步进行此操作。prover 从声明 sum(V313∗W31)=83 开始（请记住：这与说 V32(p32)=83 相同）。prover 计算并提供对于 x∈{0,1,2,3,4} 的 sum(V313(x,...)∗W31(x,...)) 的五个部分和。prover 获得一个随机坐标 c0=9，并从 V313(9,...) 和 W31(9,...) 计算半尺寸超立方体。然后，prover 重复此操作。

verifier 能够根据上一步检查每一步。特别是：

• verifier 可以将前两个总和（上表中 x=0 和 x=1）加起来，并根据前一轮的总和进行检查。
• 要计算后续轮次的总计，verifier 可以在五个提供的总和上进行 拉格朗日插值。如果你知道你有一个度数 <= 4 的多项式，并且你有五个已知点处的评估，你可以轻松地计算在任何其他点处的评估。

这是计算拉格朗日系数的代码：

def deg4_lagrange_weights(x):
    """
    Return weights w_0, w_1, w_2, w_3, w_4 such that
    for any degree-4 polynomial p,
    p(x) = sum_k w_k * p(k)  with k in {0, 1, 2, 3, 4}.
    """
    nodes = (0, 1, 2, 3, 4)
    denoms = (24, -6, 4, -6, 24)  # Π_{m≠k} (k - m) for k = 0,1,2,3,4
    coeffs = []
    for idx, k in enumerate(nodes):
        num = 1
        for m in nodes:
            if m != k:
                num *= (x - m)
        coeffs.append(num / denoms[idx])
    return tuple(coeffs)

你可以自己检查上面的示例，并查看每一轮中由该系数生成的系数的线性组合等于下一轮的总计（模 89）。

最后，prover 提供评估 V31(9,16,8)=39。因为 W 具有数学结构，所以 verifier 可以自己计算 W31(9,16,8)=85。然后，verifier 检查该等式（请记住：你可以通过检查随机点的评估来检查多项式之间的等式）：393∗85=87（在我们示例中所有模 89）。

我们做了什么？我们将 V32(p32)=y32 形式的未经证实的声明简化为 V31(p31)=y31 形式的未经证实的声明，所有这些都没有使用任何承诺！！！

然后，我们继续并继续进行，直到获得声明 V0(p0)=y0。因为 V0 只是输入，并且 verifier 具有输入，所以 verifier 可以直接检查。让我们以图表形式回顾整个流程：

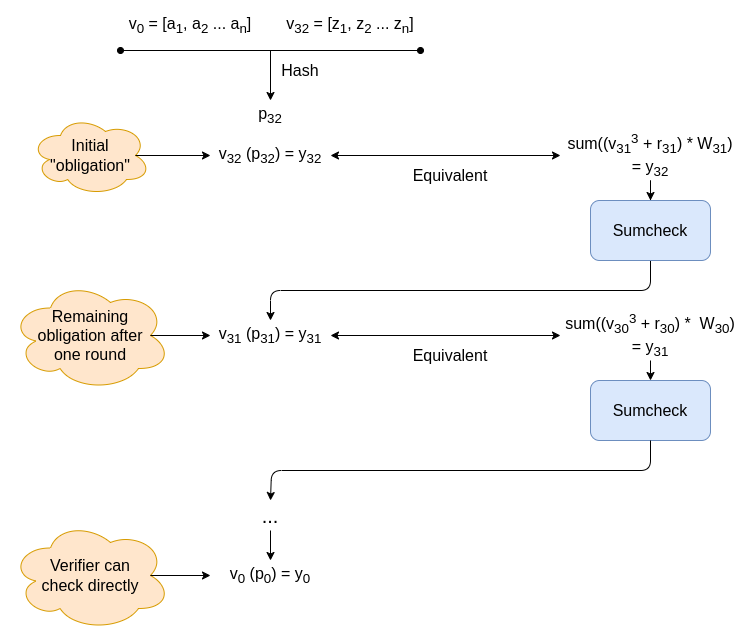
现在，让我们回到我在这里遗漏的一件事：矩阵乘法层。事实证明，有一种相当简单的方法来生成权重，这些权重表示“将 V 乘以一个矩阵 M，该矩阵仅组合同一批 16 个中的值，然后在点 p 处评估 VM”的想法。还有一种相当简单的方法来评估由这些权重生成的多项式在某个其他点 q 处，而实际上不需要计算 M（密码学家似乎喜欢《星际迷航》，因此他们有时会说“物化”M）。这对于 verifier 能够检查 Vi−1(pi−1) 和 Vi(pi−1) 之间的链接非常重要。

但是还有一种更愚蠢的方法可以做到这一点，而不会损失太多效率（实际上，它在 prover 方面_稍微_提高了效率）：只需并行运行 16 个 Sumcheck，共享相同的随机性，以便它们都获得相同的坐标。verifier 的“状态”Vi−1(pi−1) 将是一个大小为 16 的对象，并且 verifier 可以直接将矩阵应用于该对象。

优化

我们可以对上面的 sumcheck 进行重大优化，从而将每轮计算和提供的总和数从 5 个减少到 3 个。这来自两个来源。

首先，因为我们知道 verifier 可以针对之前的总数检查 sum0+sum1，所以我们可以删除 x1，并要求 verifier 自己计算 sum1=total−sum0∗(1−c)c。

第二个，更复杂的优化通常称为 Gruen 的技巧。让我们回到矩阵 W 的定义。这是一些用于计算它的 python 代码：

def generate_weights(eval_point):
    weights = [1]
    for c in eval_point[::-1]:
        R = weights[0] * c
        L = weights[0] - R
        weights = [0] * (len(weights) * 2)
        weights[::2] = L
        weights[1::2] = R
    return weights

让我们首先关注第一轮。请注意，此计算中唯一取决于第一个坐标的部分是最后一步。如果 prover 使用 W 的半尺寸版本计算 V3∗W，而我们只是跳过最后一步，会发生什么？

以下是 Whalf 和 W 在我们的示例（来自 p=[2,7,18]）中的并排显示：

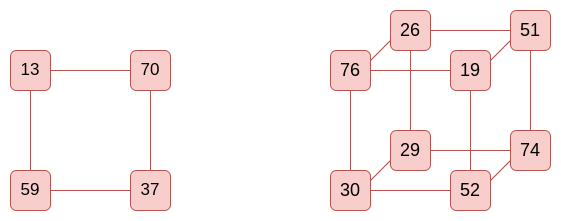
与我们之前的示例一样，这只是 [[(1−7)∗(1−18),(1−7)∗18],[7∗(1−18),7∗18]]，模 89。可以通过获取 Whalf 并乘以 x∗c+(1−x)∗(1−c) 来找到 W 在某个 x 处的评估，其中 c 是当前的评估点（在本例中为 [2,7,18] 中的 2）。在 x=0 处，这仅意味着乘以 1−2=−1（模 89），你应该能够直观地检查右侧的正面是否完全是那个。

你可以对 W 的线性组合执行相同的操作：给定总和 hsumx=sum(V313(x,...)∗Whalf(...))，你可以将其乘以 x∗c+(1−x)∗(1−c) 以获得“真实总和”sumx=sum(V313(x,...)∗W31(x,...))。

这是允许 prover 发送四个值而不是五个值的另一种方法：因为 Whalf 与当前维度无关，所以其评估对于 V 的上半部分和下半部分，以及对于扩展 V(2,...) 将是相同的。这意味着，在当前维度中，V3∗Whalf 仅是 3 阶的（而不是 4 阶的），因此你只需要四个值（hsum0...hsum3）即可用拉格朗日系数计算 hsumc。

为了针对先前的总数进行检查，verifier 将检查 hsum0∗(1−c)+hsum1∗c=total 是否成立。但是，更好的是，我们可以结合这两个技巧，让 prover 仅发送三个值！我们通过允许 verifier 自己计算 hsum1=total−hsum0∗(1−c)c 来完成此操作。

第三个较小的优化是，当 ri 不为零时，我们不需要在 sumcheck 中处理它；相反，verifier 可以简单地在适当的时间从 Vi(pi) 中减去它。

转移到“真实”的 Poseidon2

优化的下一个来源来自转移到 Poseidon2 的真实版本，其中四分之三的层每轮只立方一个值。这意味着每轮中有 16 个值中的 15 个保持不变。

不幸的是，我们不能完全跳过对它们的 sumcheck，因为如果立方值评估点从 pi 移动到 pi−1，我们也需要移动其他值的评估点。但好消息是（使用 Gruen 的技巧），它只是一个线性 sumcheck。更好的消息是你可以对其进行批量处理：你可以通过证明对于某些随机 α 的 sum(∑j=115V(i,j)∗αj 来证明 sum(V(i,1))...sum(V(i,15))。因此，prover 的大部分工作只是计算随机线性组合 ∑j=115V(i,j)∗αj。V(i,0) 被立方，因此必须使用三次 sumcheck（但共享相同的随机性）进行处理，但这现在的成本要低得多。

你可以在此处找到一些实现这些算法的示例代码：<https://github.com/ethereum/research/tree/master/gkr>

多项式承诺

在上面的分析中，我忽略了一件事，即在此示例中，verifier 正在“明确地”处理完整的输入和输出列表。对于像这样编写的协议要保证安全，这意味着 verifier 必须哈希整个列表以生成 Fiat-Shamir 随机性。因此，要接收 N 个哈希评估的证明，verifier 必须计算... N 个哈希。

在现实世界的协议中，没有人对孤立的许多哈希评估感兴趣。相反，目的是证明哈希，然后将哈希输入和哈希输出的集合公开为“查找表”，该表可用于证明包含这些哈希的更大的计算。

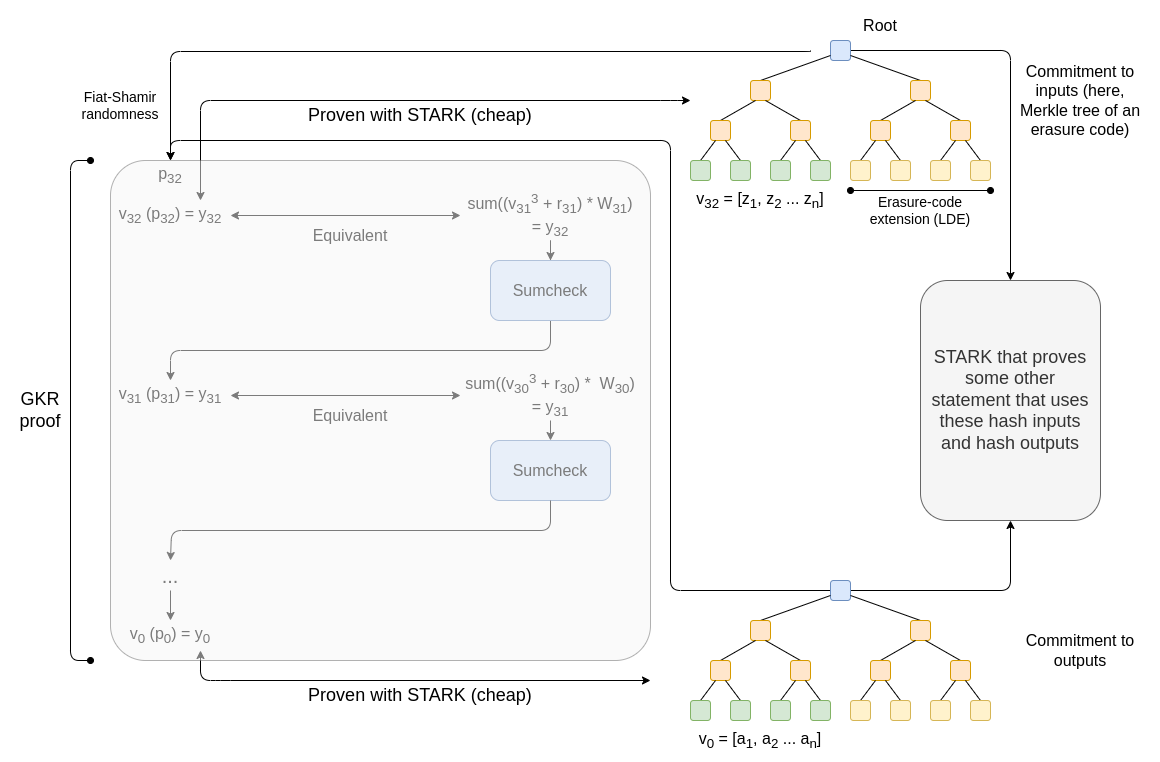
为此，你可以“只使用 FRI”。verifier 需要获得 V32(p32) 和 V0(p0) 的证明，这将转换为承诺中编码的值的线性组合。这可以完成，并且肯定比在 FRI 中证明哈希更快。另一种方法是使用多线性多项式本身的多项式承诺方案。一种常见的方法是 BaseFold，尽管还有其他更新的改进（例如 WHIR）。实际上，选择取决于你用于计算的非哈希部分哪种证明系统。

一个重要的安全考虑因素是 2025 年的一项观察：如果被证明的电路也可以在其自身的深度内足够快地计算用于导出挑战的 Fiat-Shamir 哈希，则恶意 prover 可能会预测挑战，从而欺骗证明系统。这对于像上面示例中那样使用 GKR 来证明哈希没有问题，因为 (i) 该方案是围绕一个固定电路设计的，该电路不会为攻击者利用这些技巧创造空间，并且 (ii) 该攻击涉及向 GKR 提供一个在内部计算哈希和其他计算的电路，因此根据定义，一个纯哈希电路中没有足够的深度来执行它。但是，对于更复杂和通用的 GKR 用例来说，这是一个问题；一种缓解措施是调整用于计算 Fiat-Shamir 挑战的哈希，使其需要比电路具有的回合数更多的回合来计算。

GKR 的效率如何？

让我们继续关注证明 Poseidon 哈希的用例。这是我制作的一个电子表格，其中列出了我制作的 演示实现 的所有成本：

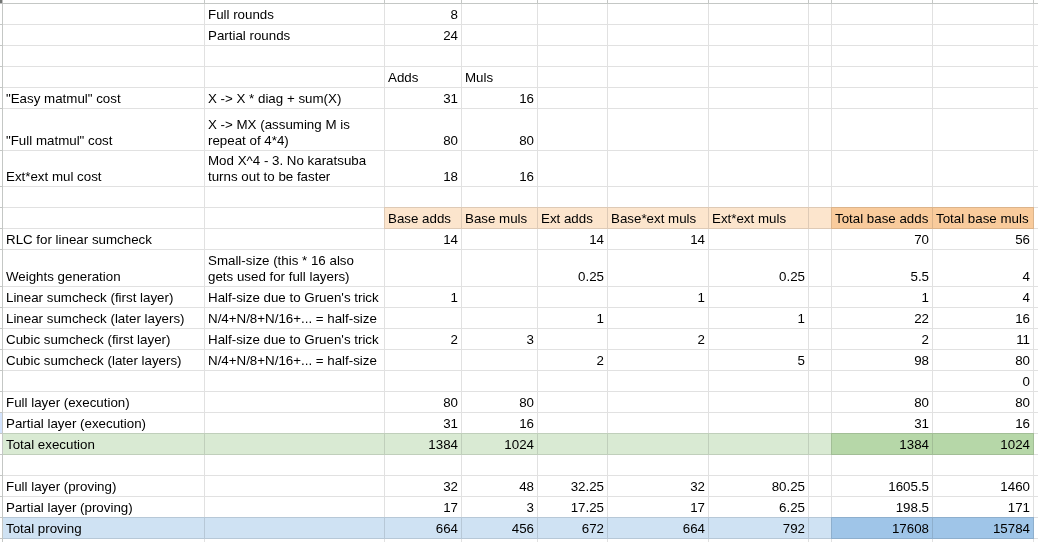
大约是 15 倍的理论开销（!!）。相比之下，使用传统的 STARK 证明 Poseidon 的理论开销约为 100 倍。收益来自于传统 STARK 证明的最大成本（请参阅 我在此处的 prover，请参阅 我在此处的理论计算电子表格 的“常规 STARK”选项卡）来自于哈希和 FFT 由所有中间值组成的跟踪数据（尽管有一个巧妙的技巧允许证明每内部轮次只需要一个跟踪值）。因此，我们根本不必做任何这些：prover 只是对输入和输出进行承诺，对于中间的所有内容，prover 每轮只是做一个 （轻得多的）Sumcheck，而对于线性工作（即 matmul），Prover 根本不需要做任何事情。

但这些数字只是理论。实践中可能与理论不同的原因主要有两个，它们朝相反的方向发展：

1. Sumcheck 比朴素哈希需要的更复杂，内存密集度更高的内存重排。在实践中，Sumcheck 通常受内存限制。
2. 实际的哈希工作负载通常至少是部分串行的，而 sumcheck 可以大规模并行化。

最重要的是，其中一个可能在给定的软件或硬件环境中更难优化。我的实现与理论相符吗？好吧，让我们看看：

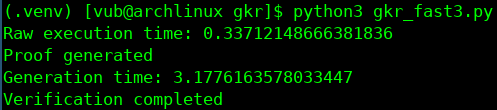
低于 10 倍！！！虽然我不会将此数字视为“真实开销”；它最有可能意味着我对原始执行的实现未经过优化。

现在，仍然有一些我们尚未尝试的优化。特别是，你可以调整 sumcheck，以便“超立方体”是一个不平衡的棱柱，其中第一维的大小大于 2。这使第一轮更大，但使所有后续回合更小；这种权衡是好的，因为在第一轮中，V 在基础 KoalaBear 素数域中，而在以后的回合中，所有内容都在扩展域中，这要昂贵得多。如果要哈希大量数据，你也可以放弃 2→1 结构，而哈希 例如 4→1 甚至更多；随着宽度的增加，GKR 的开销接近于零（!!!）。

因此，使用个位数的开销来证明哈希是非常有可能的。

在这篇文章中，哈希只是一个例子；GKR 是一系列技术，非常适合于证明许多类型的计算。如果一个计算可以用“批处理和层”的格式表示，其中每一层可以表示为一个低阶多项式，那么可以直接应用 GKR。但是，即使大型计算中不同值之间存在交叉交互，通常也可以使用一些技巧。这与证明 LLM 推理和许多其他情况有关。大多数力求非常高的效率和非常低的开销的 provers 都将在某种形式中使用类似于 GKR 的东西。

• 原文链接： vitalik.eth.limo/general...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～