ZK数学101:椭圆曲线离散对数问题
- Cyfrin
- 发布于 2025-09-05 21:59
- 阅读 1384
本文介绍了有限域上的椭圆曲线,解释了其如何构成循环群以及其同态性质,并探讨了离散对数问题如何提供加密安全性。文章详细阐述了椭圆曲线在有限域上的点加法和标量乘法,以及椭圆曲线离散对数问题(ECDLP)的计算难度,这为现代公钥密码学奠定了基础。
学习椭圆曲线如何形成循环群,探索它们的同态性质,并了解离散对数问题如何提供密码学安全。 我们之前的文章 介绍了实数域上的椭圆曲线。然而,像 ECDSA 签名和零知识证明系统这样的密码学应用需要在有限域上工作。 本文将探讨有限域上的椭圆曲线,这些离散曲线如何形成循环群,它们的同态性质,以及离散对数问题如何提供密码学安全。
有限域上的椭圆曲线
| 既然已经定义了实数域上椭圆曲线的点加法和标量点乘法,让我们在考虑有限域上的椭圆曲线时重复这个练习,其中 x 和 y 坐标来自有限域 𝕡Fp,其中 p 必须是素数才能形成一个域。 这就是椭圆曲线点,具体来说,是整数模 p=19 的有限集上的椭圆曲线,即 F19: x 值 | y 值 |
|---|---|
| 0 | 1,18 |
| 2 | 7,12 |
| 5 | 6,13 |
| 7 | 3,16 |
| 9 | 6,13 |
| 10 | 2,17 |
| 13 | 7,12 |
| 17 | 8,11 |
| 18 | 5,14 |
或者,绘制在曲线上:
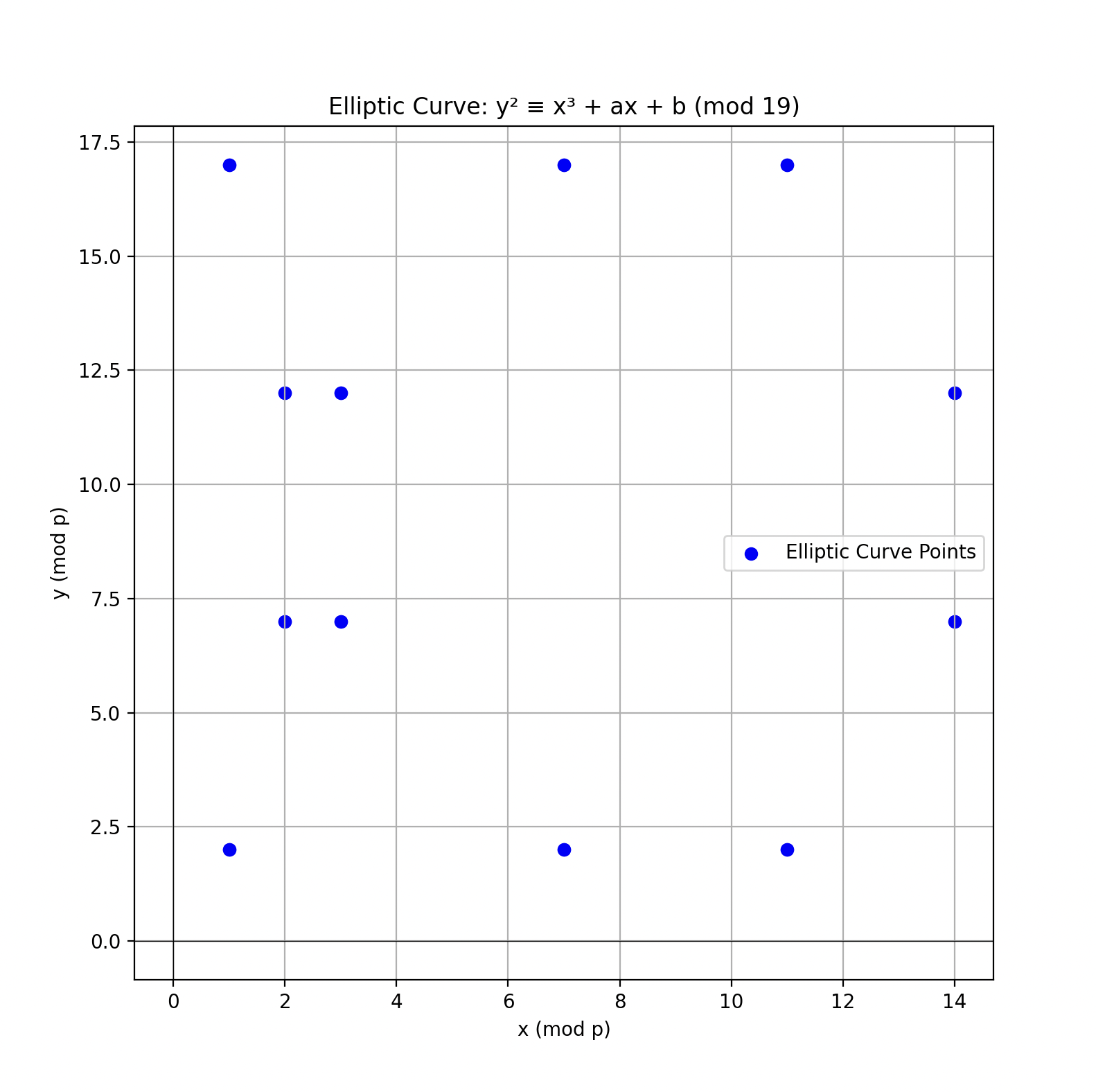 图 1:有限域 \mathbb{F_{19}} 上的椭圆曲线
图 1:有限域 \mathbb{F_{19}} 上的椭圆曲线
x 有 (p−1) 个可能值,y 有 (p−1) 个可能值。因此,椭圆曲线上的每个坐标 x 和 y 都是这个包含 p−1 个元素的集合的一个元素。 注意,与实数域上的椭圆曲线一样,该图关于 x 轴对称。然而,这个图现在是离散的而不是连续的(单个、不连接的点,而不是连续的线)。这是因为 F19 域是离散的,因为域元素是模 19 的整数,而不是实数。
点加法和群性质
有限域上椭圆曲线的点加法遵循与实数域上曲线相同的代数公式。连接、相交和反射(CIR) 框架描述了底层的数学原理,但在有限域 Fp 上,这发生在代数上而不是几何上。
要添加两个点 P=(x1,y1) 和 Q=(x2,y2):
-
"连接" - 计算通过这两点的直线斜率 λ:
-
如果 P≠Q:λ=(y2−y1)(x2−x1)modp
-
如果 P=Q:λ=(3x12+a)(2y1)modp
-
-
"相交" - 找到这条 "线" 第三次与曲线相交的地方:
- x3=λ2−x1−x2modp
-
"反射" - 获取 y 分量:
- y3=λ(x1−x3)−y1modp
群性质仍然成立:
-
单位元 仍然是无穷远点,定义与之前相同。
-
将一个点加到它的逆元上,结果是单位元:无穷远点。
-
点加法仍然是封闭的、结合的和交换的。
由于这些性质成立,有限域上的椭圆曲线也形成阿贝尔群。然而,在某些情况下,该群也是循环的。
循环结构
在有限域上的椭圆曲线的情况下,当椭圆曲线的阶(点的数量)是一个素数(我们称之为 n 以区别于 𝕡Fp 中的素数域模数 p)时:
- 曲线点形成一个循环群,并且存在一个生成点 G,从中可以使用标量乘法(重复将 G 加到自身)计算每个点。
P=kG
-
曲线上的每个点 P 都可以表示为 P=kG,其中 k 是一个标量,并且 k∈0,1,2,...,n−1。
-
我们可以使用 Hasse 界 估计曲线上点的数量(它的阶)。
例如,对于一个阶为 19 的曲线,我们可以通过从生成点 G 计算 G, 2G, 3G, ..., 18G 加上无穷远点 O 来生成所有 19 个点。
椭圆曲线空间中的离散对数问题
ECDLP 是 离散对数问题(DLP)的一个版本,它考虑了具有点加法运算符的椭圆曲线点。 DLP 询问:给定一个生成元 g 和一个元素 h,找到一个整数 x ,使得将群运算应用 x 次于 g 得到 h。 在一个有限乘法循环群 中,这意味着找到 x 使得:
h=gx(modp)
其中指数运算是重复乘法。 ECDLP 是椭圆曲线群的 DLP:有限域上的椭圆曲线点的集合,配备有点加法二元运算符。 ECDLP 是确定标量 x 的问题,使得:
P=xG
其中:
-
G 是生成点(椭圆曲线上的一个已知点)
-
P 是另一个已知点
-
x 是试图找到的未知标量,它被用来生成 P
记住,这是标量乘法,所以是重复的点加法。 ECDLP 声明找到标量 x 在计算上是不可行的。
为什么 ECDLP 很难?
虽然点加法在计算上是高效的,但如果椭圆曲线的阶 n 足够大,反转这个操作(即,给定 P=xG 找到 x)是一个没有已知高效算法的问题。没有直接的 "标量除法" 公式。 给定一个点 P,不知道使用哪个标量 x 来计算它,要找到 x,你必须尝试许多可能性,直到找到正确的那个(使用像 Pollard’s Rho 算法 这样的算法,它是一种优化的蛮力方法,或穷举搜索,它将计算次数减少到 ~n)。当群的阶 n(群中元素的数量)很大时,像这样的算法变得不可行。 这就是为什么 n 必须很大:以确保可能的 x 值的空间是巨大的,使得穷举搜索在计算上不切实际。
示例:暴力破解 ECDLP
| 为了理解为什么 ECDLP 很难,考虑一个在 F5 上的小曲线,方程为 y2=x3+2x+1mod5。 假设我们选择 G=(0,1) 作为我们的生成元。我们可以计算标量倍数: x | x G |
|---|---|
| 1 | (0,1) |
| 2 | (1,3) |
| 3 | (3,3) |
| 4 | (3,2) |
| 5 | (1,2) |
如果给你 P=(3,3),要解 xG=P 中的 x,你可以尝试每个倍数:
-
1G=(0,1) ❌
-
2G=(1,3) ❌
-
3G=(3,3) ✅
因此,x=3。 在这个例子中,暴力破解 x 很容易,因为可能性非常少。但是在实际的曲线中,例如,对于 BN254 曲线,n(椭圆曲线的阶)大约是 2256,这种方法变得完全不可行。
同态性质
椭圆曲线表现出重要的同态性质,这使得它们对于密码学很有用: 标量乘法创建了一个从加法群 Zn(模曲线阶的整数)到有限域 𝕡Fp 上的椭圆曲线群的同态。 加法同态:对于任何整数 a 和 b 模曲线阶 n 和生成点 G,Zn 中的加法映射到曲线上的点加法:
(a+b)G=aG+bG
分配律:对于任何整数 k 模曲线阶 n 和点 P 和 Q,标量乘法分配到椭圆曲线点加法上:
k(P+Q)=kP+kQ
因此,我们可以通过与生成点 G 的标量乘法将私有值转换为椭圆曲线点。 生成的点保持与原始值的运算相对应的数学关系,同时使得恢复原始值在计算上不可行(由于 ECDLP)。 例如,如果我们有一个私有值 x 并生成点 P=xG,我们可以在 P 上执行与 x 的运算相对应的运算,而不泄露 x 本身。 点 P=xG 充当 x 的 "密码学表示"。 对这些表示的操作对应于对底层值的操作,但是离散对数问题使得从 P 中提取 x 在计算上不可行。 这个性质是许多密码学协议的基础,包括数字签名、密钥交换和零知识证明。
总结
本文涵盖的关键概念包括:
-
有限域:有限域 𝕡Fp 上的椭圆曲线具有离散点,其坐标来自该域。
-
循环群:当曲线阶 n 为素数时,每个点都可以从单个基点生成:生成点 G。
-
同态性质:关系 (a+b)G=aG+bG 允许私有值的结构保持变换。
-
ECDLP 难度:确定给定 P=xG 的 x 在计算上的困难提供了密码学安全性。
高效计算和计算难度的结合使得有限域上的椭圆曲线成为现代公钥密码学的基础。
参考文献
- LeastAuthority ZK Moon Math Manual
- Vitalk Buterin Elliptic Curve Pairings
- Rare Skills ZK book
- Nick Sullivan 的关于椭圆曲线密码学的 (相对容易理解的) 入门
- 原文链接: cyfrin.io/blog/zk-math-1...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 使用 Ecash 票据的谨慎日志合约 333 浏览
- Fiat-Shamir 启发式非交互式零知识证明之美(以及 Zig) 530 浏览
- 有限域之美与力量 (以及 Zig) 478 浏览
- DahLIAS:既非 ECDSA,也非 Schnorr 553 浏览
- 安全研究人员的数学指南 849 浏览
- ZK 编年史:数学基础 1511 浏览
- ZK编年史:Sum-Check 1314 浏览
- FFT友好的有限域 926 浏览
- Σ 舞步:承诺、挑战、响应 745 浏览
- 单位根的可视化表示 2091 浏览
- 单位根的平方根 1981 浏览
- k次单位根的平方是k/2次单位根 1919 浏览

