执行拍卖作为执行票证的替代方案 - 权益证明/区块提议者
- 以太坊中文
- 发布于 2024-06-25 17:53
- 阅读 556
本文对比了两种解决以太坊 MEV 问题的方案:Execution Auctions (EAs) 和 Execution Tickets (ETs)。
_作者:Jonah Burian & Davide Crapis_
特别感谢 Anders Elowsson, Barnabé Monnot, Justin Drake 和 Mike Neuder 提供的反馈和评论。
介绍
以太坊中存在委托代理问题。虽然协议创造了 MEV,但它将其泄漏给了提议者。此外,MEV 以其当前状态将协议暴露于其他外部性,例如 时间博弈。研究界普遍认为,捕获和正确重新分配 MEV 是以太坊演变的重要一步,以使协议更具弹性和效率(注意:有些人不同意)。解决这种委托代理问题的唯一方法是由协议通过可信和高效的机制出售赚取 MEV 的权利。
经过多年的研究,最近出现了两种方法,可以作为解决 MEV 燃烧的潜在途径。在这些机制中,提议执行有效负载的权利不是免费提供给 信标提议者,而是单独出售给 执行提议者。
- 执行拍卖 (EAs): 提议执行有效负载的权利是提前为每个槽 确定性地分配 的,槽执行提议者可以通过提前举行的槽拍卖中竞标来购买该权利,例如 提前 32 个槽。
-
执行彩票 (ETs): 执行提议者的权利不是确定性分配的,提议者可以提前购买彩票,然后在每个槽之前,从彩票池中随机抽取一个中奖者,并获得提议的权利。
这些机制具有相同的目标,但存在重要的差异。这篇文章的目标是比较这两种解决方案。
设置
我们将在本文中介绍公式,以概述协议之间的关键经济差异。我们还将解释实际的细微差别,因此如果你想跳过数学,请不要担心!对于额外的好奇者,我们在附录中列出了公式的证明。
术语
- t — 离散时间间隔(槽)。
- n — 彩票的数量。
-
d 是用于计算未来奖励的现值的槽间贴现率。
- 注意:假设普通的质押率是以太坊中的无风险利率,则 d \approx 10^{-8}
-
\mathcal{R} 是一个随机变量,表示在时间 t 控制执行有效负载的价值。
- 我们将其称为执行层奖励(EL 奖励),它等于槽 t 中的 MEV + 费用。
- 我们假设 \mathcal{R} 具有不随时间变化的分布,并且每次抽取都是独立的。(这在实践中通常不是这种情况,因为 EL 奖励随时间变化且相关,但它允许进行不太复杂的分析,以后可以扩展。)
- \mu_{\mathcal{R}} 是 \mathcal{R} 的期望值。
-
V_{ticket} — 单张彩票的净现值 (NPV)。
- 注意:在时间 t 实现的某个值 X 的现值计算为 \frac{X}{(1+d)^t}。
- m — 赢得提议权后,给予提议权的槽数 t(例如,m=32)。
指导原则
所有未来 EL 奖励的预期净现值为
NPV_{\mathcal{R}} = \frac{\mu_{\mathcal{R}}}{d}
这是从现在到未来以太坊所有区块空间的总价值。鉴于执行拍卖和执行彩票的目标是捕获区块空间的价值并将价值重新分配以与协议的目标保持一致,因此所有解决方案都必须根据它们捕获 NPV_{\mathcal{R}} 的程度进行分析。
注意:捕获所有价值取决于销售机制。在本分析中,我们假设销售机制是有效的。目前正在研究在动态/重复战略互动背景下对销售机制的详细分析,这是一个开放性问题。
执行拍卖
执行拍卖 (EAs) 本质上是提前进行的槽拍卖:
- 提议者权利分配: 槽 k+m 的 执行提议者权利 在提前 m 个槽,即槽 k 时出售。
- 销售机制: 槽 k 的信标提议者收到该权利的投标,并承诺接受最高出价,证明者投票。
很可能会发展出一个 二级市场,EA 彩票的中奖者可以在轮到他们提议之前转售他们的提议权。即使协议不允许他们转移该权利,也可以通过协议外的工具轻松完成。
执行彩票
执行彩票 (ETs) 具有彩票组件,该组件增加了持有者未来能够提议的特定区块的不确定性,可以在更接近提议时间或更早的时间解决此问题。
- 提议者权利分配: 未来 某个槽 的 执行提议者权利 以彩票的形式出售。
-
销售机制: 假设彩票池中已经有 n 张彩票,在每个槽中,一张彩票被选为彩票中奖者(例如,在槽结束时使用 RANDAO),并且从下一个槽开始出售一张新彩票进入彩票池。
- 定价: 为了与 EA 进行比较,我们假设采用英式拍卖。
- 不确定性解决: 我们可以拥有下一个槽执行彩票,即在槽 k 结束时,我们选择槽 k+1 的提议者(我们将其称为 sET,即简单 ET),或者未来槽执行彩票,即在槽 k 结束时,我们选择槽 k+m 的提议者(我们将其称为 ET)。
与 EA 类似,很可能会出现一个二级市场,彩票持有人或中奖彩票持有人可以转售他们参与彩票或提议的权利。
注意:在最初的文章执行彩票的经济分析中,我们尚未区分 sET 和 ET。那篇文章是关于 sET(ET 的一个特例)。
注意 2:Justin 敏锐地指出,我们不知道如何使用 RANDAO 实现低延迟随机性,VDF 也无济于事。低延迟 RANDAO 将是可偏袒的(当你连续控制两个槽时,它也是完全可预测的)。
分析
注意:所有近似都假设 m(从彩票中奖到授予权利的时间)和 n(ET 的数量)不大。鉴于 d 接近于零,我们能够简化方程。
注意 2:如果不使用近似值,EA 彩票和 ET 都有一些与以下事实相关的无谓损失:中奖彩票不能立即使用,即考虑到时间折扣,存在一些损失。近似值的直觉是,鉴于 d 很小,因此由于时间折扣造成的这种价值损失名义上的。
注意 3:虽然我们在 sET 和 ET 的方差近似中假设 n 很小,但我们在“执行彩票的经济分析”中讨论过,大的 n 会导致更少的中心化风险,并且在谁能负担得起彩票方面更加民主。也就是说,大的 n 会产生估值复杂性,并增加了必须在彩票开始时进行大规模销售以引导彩票池的额外复杂性。(阅读文章以了解更多信息。)
这是一个简化版本的图表,假设进行了近似。
请注意,所有三种使用近似的方法都得出了相同的结论:我们可以有效地捕获(假设有一个有效的拍卖)与区块空间相关的所有价值。此外,在每种设计中,彩票都有一个简单的解释:它们大约相当于与提议执行有效负载相关的价值。
彩票价值的方差是每个槽的奖励的方差,考虑到提议权是提前出售的,即在区块构建之前,这几乎是你能得到的最好的结果。
确定事项 vs 未来可能性:比较 EA 和 sET/ET
现在,我们来比较 EA 和 sET/ET,以阐明在考虑在实践中实施此类机制时的权衡。应该注意的是,大多数权衡都来自 EA 和 sET/ET 之间的根本区别——前者是确定性协议,而后者利用非确定性。
- 实施简单性: EA 更易于实施,彩票不需要随机性,因此无需担心 RANDAO 偏差。此外,目前尚不清楚如何实现 sET 的随机性。EA 彩票的提议者权利二级市场将比 sET/ET 简单得多,无需担心彩票 MEV。此外,似乎有一条 通过 ePBS 实施 EA 的清晰路径,并且由于我们出售的是未来槽,因此可绕过性不是问题。
- 更简单的资产: 与随机资产相比,更容易推断确定性资产,这使得 EA 比 sET 和 ETS 更好。也就是说,协议中的买家很可能是老练的,并且当前选择验证者的范例依赖于随机性,这意味着维持非确定性不会与现状有实质性的决裂。但是,一个反驳的论点是,当前的提议者可能不是彩票的买家。
- 方差可能会影响估值,并且 EA 彩票的风险较低: 彩票持有人对彩票应用风险折扣是合理的;也就是说,考虑到风险规避,他们可能会降低彩票的价值。虽然 EA 彩票仅暴露于槽 t+m 中 EL 奖励价值的方差,但 sET 和 ET 都暴露于 EL 奖励中的方差以及彩票中奖时间的方差。直观地说,因此 EA 的风险折扣最低。
- 效率: 从协议的角度来看,sET 更有效,因为提议者权利在预期中更接近 MEV 的槽出售,而 EA 和 ET 在理论上存在无谓损失。也就是说,在考虑风险规避的情况下,EA 可能会更有效。
- 预确认(Preconfs): 预确认需要有一个前瞻,这意味着协议必须提前知道谁将控制执行有效负载的权利。虽然 EA 和 ET 允许预确认,但 sET 不允许,因为中奖者是在每个区块中确定的。
-
控制成本:
- 在 EA 中
- EA 将 交易活性 风险置于以太坊之上——也就是说,垄断区块空间的成本与以太坊的安全预算脱节,并且控制连续区块的成本具有固定值。连续控制 x 个区块的成本约为 \approx x\mu_{\mathcal{R}}。幸运的是,新的 IL 设计 可以纠正这一点。即使有了 IL,过度依赖它们也是不理想的(它们旨在作为最后的手段,而不是司空见惯——这可以争论)。同样重要的是,持续控制多个槽的能力意味着资金充足的当事方将永久赢得更多区块空间。这可能会导致执行有效负载构建管道的中心化,从而加剧该管道中当前的中心化挑战。(请参阅“MEV 的未来”中的多区块 MEV 部分)。
- Barnabé 恰当地向我们指出,说“垄断区块空间的成本与以太坊的安全预算脱节”与验证者可以出售构建权的现有设置没有什么不同。目前,验证者可以连续出售多个区块。这并不意味着中心化论点不正确,但表明 EA 与现状没有实质性的决裂。
- 在 sET 中(和 ET):
-
虽然垄断区块空间的成本与 sET 的安全预算脱节(和 ET),但成本要高得多,并且单个当事方不太可能连续控制多个区块。非确定性阻止了对区块空间的有保证的控制,从而降低了控制的可能性。随机性是对抗中心化的防御。
- 第一个图表提供了对此原则的直观理解。它显示了一个有 100 个未完成的 sET/ET 的情况。如果某人拥有 95% 的初始未完成彩票(请记住,随后每个区块会铸造一张彩票),则连续赢得 20 个槽的概率约为 4%,而连续赢得 35 个槽的概率几乎是不可能的。
- 此外,控制 P\% 的区块的成本随着 n 的增加而增加(请参阅:执行彩票的经济分析)
- ET 的不同之处:
- 虽然 sET 中的攻击者必须依靠机会赢得连续的区块,但聪明的 ET 用户可以在二级市场上购买 t+m 到 t+m+x 的一系列中奖彩票,从而使 ET 中的中心化类似于 EA 中的中心化问题。有人可能会说,sET 承受着与协议外拍卖控制 sET 获奖者权利相同的风险。也就是说,可能存在不出售执行有效负载构建权的诚实参与者。如果其中一位持有人中奖,他们将结束 sET 攻击者的连续中奖区块,这意味着即使有协议外选项,sET 攻击也会暴露于不确定性中。
结论
EA 在简单性方面占主导地位,而 sET 可以防止中心化,但代价是不允许预确认。鉴于 RANDAO 问题,sET 也可能无法在当今的以太坊协议中实施。IL 可以遏制 EA 的中心化问题,而 sET/ET 的二级市场可以消除其保护性优势。此外,EA 在中心化方面与现状没有实质性的决裂。
虽然围绕实施 EA 及其效率仍存在一些开放性问题,但对于以太坊协议而言,EA 似乎优于 sET 和 ET。
相关工作
此列表是从 关于区块空间分配机制 复制粘贴的,并添加了 关于区块空间分配机制。哈哈
- mev-boost & 中继
- MEV-Boost:合并就绪的 Flashbots 架构;Flashbots 团队
- 后 ePBS 世界中的中继;Mike、Jon、Hasu、Tomasz、Chris、Toni
- mev-burn / mev-smoothing
- 通过区块提议者拍卖燃烧 MEV;Domothy
- MEV 燃烧——一个简单的设计;Justin
- 委员会驱动的 MEV 平滑;Francesco
- Dr. changestuff 或:我如何学会停止担心并热爱 mev-burn;Mike、Toni、Justin
- 神圣化的提议者-构建者分离 (ePBS)
- 双槽提议者/构建者分离;Vitalik
- 解绑 PBS:迈向协议强制执行的提议者承诺 (PEPC);Barnabé
- 关于提议者-构建者分离的注释;Barnabé
- 更多关于提议者和构建者的图片;Barnabé
- 为什么要神圣化提议者-构建者分离?;Mike、Justin
- ePBS 设计约束;Potuz
- 重新考虑 PBS 的市场结构;Barnabé
- 区块空间期货
- 区块 vs. 槽拍卖 PBS;Julian
- 以太坊区块空间未来的机遇与考量;Drew、Ankit
- 何时出售你的区块;Quintus、Conor
- 执行彩票
- 证明者-提议者分离;Justin
- 执行彩票;Justin、Mike
- 执行彩票的经济分析;Jonah、Davide
- 区块拍卖 ePBS 与执行彩票;Terence
- 关于区块空间分配机制;Mike、Pranav 和 Tim Roughgarden 博士
这篇文章的目标与 Mike, Pranav, & Tim 最近题为 关于区块空间分配机制 的工作类似:比较用于执行权利分配的新机制。 但是,我们的分析中有一些关键差异,我们在此处重点介绍:
- 他们使用修改后的 ET 模型(即,所有彩票都在槽之间销毁的模型)。虽然此模型更易于实施,但不会导致有效的分配(因为对区块空间的估值较低的人仍然可以分配到区块空间)。
- 他们专注于 Tullock 竞赛模型,而我们的模型类似于固定收益模型。
- 他们的分析侧重于协议内 MEV 预言机的质量与机制的公平性之间的权衡,而我们侧重于其他权衡,例如实施的简易性、风险折扣、中心化控制和经济效率。
附录
计算贴现率:
本文发表时的质押率为~3.4%(来源)。
1.34=(1+d)^{\text{一年中的槽数}}=(1+d)^{365 * 24 * 60 * 60 / 12} d=1.27e-08 \approx 10^{-8}
d=1.27e-08 \approx 10^{-8}
所有未来 EL 奖励的预期净现值:
有关证明,请参阅此 论文
计算: E[V_{\text{EA 彩票}}]
E[V_{\text{EA 彩票}}] = \frac{\mu_{\mathcal{R}}}{(1+d)^m}
这是因为该价值在 m 个槽之后被确认,因此你需要将 m 个区块中收到的 MEV 按贴现率 d 进行贴现。
计算 E[V_{\text{所有 EA 彩票}}]
\begin{align*}
E[V_{\text{所有 EA 彩票}}] &=
\sum_{t=1}^{\infty} \frac{ E[V_{\text{EA 彩票}}]}{(1+d)^t} \\\
&= \sum_{t=1}^{\infty} \frac{\mu_{\mathcal{R}}}{(1+d)^{m+t}} \\\
&= \frac{1}{(1+d)^{m}} \sum_{t=1}^{\infty} \frac{\mu_{\mathcal{R}}}{(1+d)^{t}} \\\
&= \frac{1}{(1+d)^{m}} NPV_{\mathcal{R}}
\end{align*}计算\text{Var}(V_{\text{EA 彩票}})
\text{Var}(V_{\text{EA 彩票}}) = \text{Var}\left(\mathcal{\frac{R}{(1+d)^m}}\right) = \frac{\text{Var}(\mathcal{R})}{(1+d)^{2m}}
计算 NPV_{\mathcal{R}}, E[V_{\text{sET}}], E[V_{\text{所有 sETs}}] 和 \text{Var}(V_{\text{sET}})
证明可以在 Jonah 的“MEV 的未来”论文中找到。请记住,该论文没有区分 sET 与 ET。
计算 E[V_{\text{ET}}], E[V_{\text{所有 ETs}}] 和 \text{Var}(V_{\text{ET}}),
这些是使用 m 槽折扣对 sET 计算的简单修改。
计算图 1:
当最初持有 sET/ET 的 p 个百分比(每个区块不回购彩票)时,赢得 m 个连续槽的概率由赢得每个独立抽奖的概率的乘积确定:
\begin{align*}W &= \left(\frac{pn}{n}\right) \cdot \left(\frac{pn-1}{n}\right) \cdot \left(\frac{pn-2}{n}\right) \cdots \left(\frac{pn-(m-1)}{n}\right) \\\\&= \frac{(pn)!}{(pn-m)! n^m}\end{align*}计算图 2:
请参阅“MEV 的未来”论文中的第 4.4 节。
- 原文链接: ethresear.ch/t/execution...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 翻译
- 学分: 0
- 分类: 以太坊
- 标签: MEV Execution Auctions Execution Tickets 以太坊 区块空间 中心化
- 我们的 2026 年路线图 53 浏览
- 作为基础设施的以太坊、Vitalik谈去中心化与用户体验、无需信任的互操作性、7702 & 4337... 160 浏览
- 第12章:再质押(Restaking) 34 浏览
- 第11章:流动性质押协议 20 浏览
- 玻璃屋中的幽灵——为什么DeFi市场永不遗忘 259 浏览
- DeFi 安全最佳实践 350 浏览
- Uniswap The Compact 审计 295 浏览
- EIP-7702 驱动的极简代理实现 397 浏览
- 审计 Uniswap V4 Hooks:风险、利用与安全实现 378 浏览
- 以太坊:世界金融新后端 357 浏览
- Vitalik: 权力制衡 223 浏览
- 公链共识算法DPoS和PoS的比较分析 330 浏览
 \
ealien1024×1024 128 KB
\
ealien1024×1024 128 KB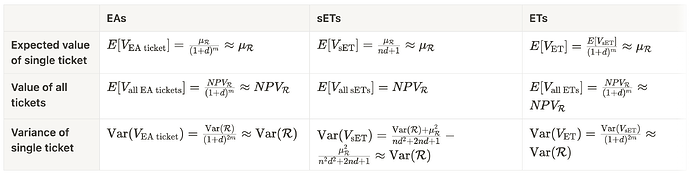 \
Chart 12514×636 104 KB
\
Chart 12514×636 104 KB \
Chart 21286×464 29.2 KB
\
Chart 21286×464 29.2 KB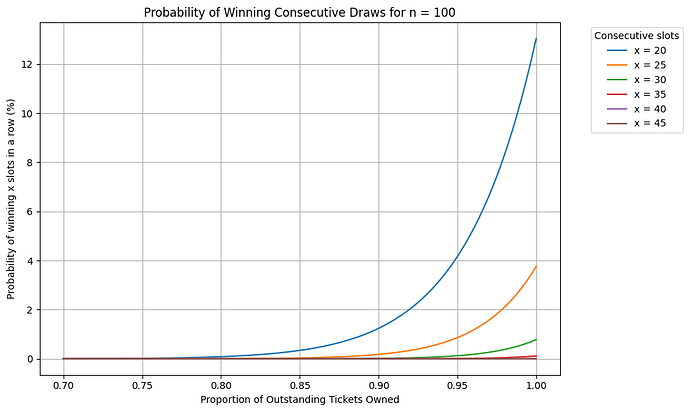 \
Graph 1988×590 37 KB
\
Graph 1988×590 37 KB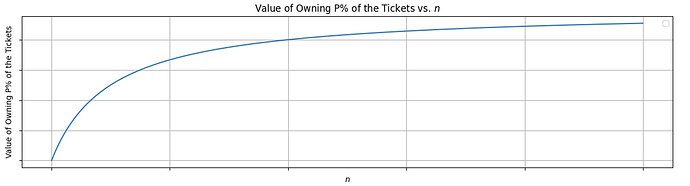 \
Graph 21380×372 18 KB
\
Graph 21380×372 18 KB
