安全多方计算 (sMPC) - 无需共享的协作
- mabeloza
- 发布于 2022-10-17 17:16
- 阅读 784
本文深入探讨了安全多方计算(sMPC)技术,它允许多方在不泄露各自数据的前提下协同计算。文章介绍了sMPC的基本概念、应用场景(如糖 beet 拍卖、薪资公平性分析、密钥管理),并详细解释了姚百万富翁问题、同态加密(PHE、SHE、FHE)以及阈值签名(TSS)等关键技术。此外,还介绍了混淆电路、不经意传输(OT)以及几种MPC的具体实现方案,如姚氏协议、PSI和MPC CMP。
安全多方计算 (sMPC) — 无需共享的协作

一个计算机聚会在新年前夜……2000年
分析大数据的下一步是共享数据,这会带来创新。共享数据使我们能够创造让生活更轻松的产品(感谢自动驾驶汽车、健康建议,以及那些完美总结我们深夜复杂思绪的 Tik-Tok 短视频等等)。
一切都很好,直到我们被背叛,有人将我们的数据分享给黑暗势力(咳咳……2020年美国大选)。这就是为什么隐私至关重要,以及为什么许多组织开始拥抱隐私增强技术 (PET)。隐私技术是一个广泛的领域,范围从零知识证明到环签名,今天,我们将只关注安全多方计算 (sMPC)。
💻 什么是安全多方计算?** ](#3444)
💰 姚氏百万富翁问题** ](#1cbc)
👨👦👦 阈值签名 (TSS)** ](#3444)
🏬 不同的 MPC 实现** ](#0374)
什么是安全多方计算 (sMPC)?
MPC 的简化描述是,它是一种软件解决方案,允许多方协作获得答案,而无需相互泄露他们的数据。
安全多方计算 (MPC) 使一组互不信任或不信任任何共同第三方的独立数据所有者能够共同计算一个依赖于他们所有私有输入的函数。
- 安全计算, Wei Jiang
用例
多方计算已经存在多年,并且在区块链和加密货币领域之外有多种应用,包括广告优化、机器学习等。以下是 MPC 的一些值得注意的用例。
甜菜私人拍卖

照片由 Nick Collins 在 Unsplash 上拍摄
该技术的第一个大规模商业应用是在丹麦的密封投标甜菜拍卖中用于保护隐私。
在这种类型的拍卖中,出价最高者获胜,但支付第二高出价者提出的价格。
MPC 使甜菜种植者能够在不透露他们愿意支付的价格的情况下向当时丹麦唯一的甜菜加工商 Danisco 提交投标。
https://csrc.nist.gov/csrc/media/events/meeting-on-privacy-enhancing-cryptography/documents/toft.pdf
薪资不平等
波士顿市和波士顿妇女劳动力委员会 (BWWC) 需要确定不同性别和种族在不同就业水平(从高管到入门级)之间的薪资不平等。为了防止任何人的薪资在此研究中被暴露,波士顿大学创建了一个工具,允许雇主私下提交薪资数据。这项工作间接促使国会将安全多方计算作为“2017 年学生知情权法案”的考虑因素。

从国会法案中截取:https://www.congress.gov/bill/115th-congress/senate-bill/2169/text
密钥管理
如今,许多保护加密资产的公司都依赖 MPC 技术,包括 PayPal、Facebook、Coinbase 和 BNY Mellon(基于他们收购或宣布与 Curv、Unbound 等 MPC 公司建立关系的事实)。
关于加密资产的一点说明……
加密资产由密钥对(公钥和私钥)表示。加密钱包地址从公钥派生,公钥从私钥派生。
诀窍是你不能反向操作,你永远不能使用地址或公钥来推导出私钥。拥有私钥的人可以证明对加密资产的所有权并签署交易(这实际上意味着他们可以花费/发送加密货币)。
因此有了“不是你的密钥,就不是你的币”这句话。
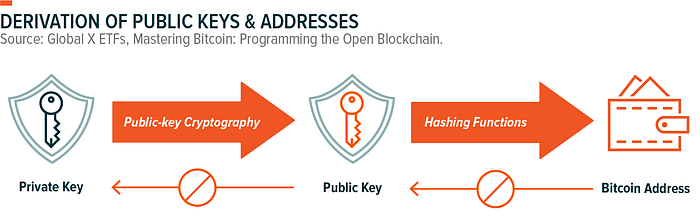
图片来自 https://www.globalxetfs.com/bitcoin-the-basics/
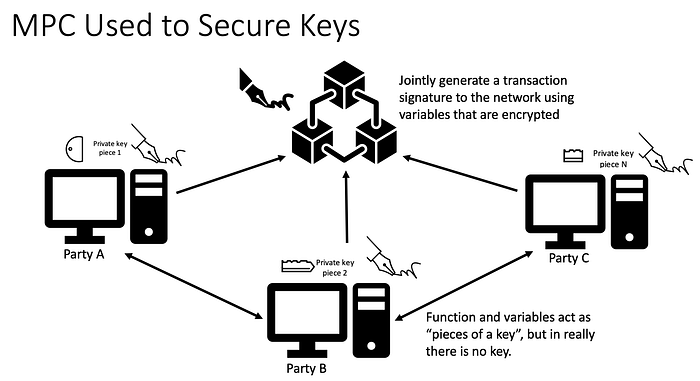
MPC 用于防止加密密钥出现“单点泄露”,没有一个设备或方可以单独拥有或花费加密货币。每个方(机器或实体)使用他们的“拼图碎片”共同为交易生成单个签名。
剧情反转: 在此解决方案中,永远没有实际的密钥,它们使用模拟密钥片段操作的变量。
另一个剧情反转: 代表密钥片段的变量永远不会在一个地方组合。相反,他们使用同态加密来共同创建密钥片段的相似之处并签署交易。
以下是一些在加密资产领域解决 MPC 的开源库:
Unbound 的实验性 MPC 实现 — 当前已存档 (自 2021 年起)
GitHub — unboundsecurity/blockchain-crypto-mpc: Protecting cryptographic signing keys and seed…
ZenGo 的基于 Signal 的 MPC
GitHub — ZenGo-X/mpc-over-signal: Secure transport for running MPC protocols backed by Signal
ZenGo 的 MPC ECDSA
GitHub — ZenGo-X/multi-party-ecdsa: Rust implementation of {t,n}-threshold ECDSA (elliptic curve…
Taurus Groups — 使用 CGGMP 实现
GitHub — taurusgroup/multi-party-sig: Implementation of protocols for threshold signatures
姚氏百万富翁问题
1982 年,姚启智引入了姚氏百万富翁问题,其中 Bob 和 Alice 想知道谁更富有,但永远不会向对方透露他们的财富。为了解决百万富翁问题,姚启智提出了一个基于混淆电路的两方计算 (2PC) 协议。
姚氏百万富翁问题 — Alice 和 Bob 的平均净资产是多少?
在这种情况下,我们将尝试找到 Alice 和 Bob 之间的平均财富。我们不希望 Bob 或 Alice 透露他们的财富,这就是 sMPC(安全多方计算)发挥作用的地方。
- Alice 和 Bob 将他们的财富分成秘密份额,这些份额是随机的,并且总和等于他们的财富(即,Alice 的秘密份额为 200 万美元 + 600 万美元 + -300 万美元 = 500 万美元)

-
Alice 和 Bob 随机地将他们的份额分发给对方,此时,这些份额对彼此没有任何意义。
-
Alice 和 Bob 将他们所有的份额相加(即,Alice 的份额包括 Bob 的 500,000 美元的秘密份额和她自己的 200 万美元和 600 万美元的份额,加起来总共 850 万美元)。

- Alice 和 Bob 结合他们从步骤 2 中获得的结果,即他们的份额的加法结果,并计算他们的薪水的平均值。

免责声明:这是对 MPC 和姚氏百万富翁问题的过于简化的解释.
同态加密
为了保护隐私,我们需要使用加密后的数据,而无需对其进行解密和查看,这就是同态加密的用武之地。
同态加密允许在 加密 数据上执行数学运算(布尔运算和算术运算),而不会损害加密。

同态加密的目标
在允许对加密数据进行有限次数的加法或乘法运算后,它必须提供与未加密时相同的结果。
“所以,基本上,任何人都可以来,他们可以将手伸进手套里,操纵锁定的盒子里的东西。他们无法将其拉出,但他们可以操纵它;他们可以处理它。他们可以获取原材料并在盒子内制作项链或其他东西。而且,你知道,他们完成了,然后 [拥有私钥的人] 必须带着秘密密钥来打开它,只有他们才能从中提取成品。"
- Craig Gentry 博士

同态加密的类型
同态加密有三种类型:部分 同态 (PHE)、一定程度 同态 (SHE) 和 完全 同态加密 (FHE)。 它们的不同之处在于对加密数据执行的数学运算的类型和频率。

部分同态 (PHE)
PHE 仅允许对加密的值执行选择的数学函数。 这意味着只能对加密数据执行一个操作,无论是加法还是乘法,次数不限。 此操作只能是加法或乘法。
选择你的毒药: 选择一个操作,你可以无限次地使用它
密文 1 + 密文 2 + 密文 3 +… + 密文 NPHE 的一些示例包括 RSA 加密(乘法同态*)、Pallier 加密(加法同态)和 ElGamal 加密(乘法同态)。
- RSA 基于取幂:C = (m^x) (mod n),其中 m 是消息,x 是密钥。 指数的规则表明 (a^n)(b^n)=(ab)^n。 这意味着将两个用相同密钥加密的密文相乘等同于将明文的乘积提升到密钥的幂。
一定程度同态 (SHE)
SHE 支持有限的操作(例如,加法 或 乘法),达到一定的复杂性,但这些操作只能执行一定的次数。
例如,某种程度的同态加密算法可以支持最多四次加法或乘法的任意组合。 但是,第五次操作(无论是哪种类型)都会产生无效的结果。
选择你的毒药: 选择一个操作组合,并使用设定的次数。
密文 1 + 密文 2 x 密文 3 + 密文 4全同态 (FHE)
使用全同态加密,你可以拥有所有内容、操作的组合并无限期地运行它们。 主要的 FHE 方案基于 LWE(Learning With Errors)、Ring-LWE、NTRU 和 Approximate-GCD 问题。
选择你的毒药: 选择一个操作组合,并无限期地使用它
密文 1 + 密文 2 x 密文 3 x … + 密文 NCraig Gentry 博士提出了基于 格密码学 的第一个 FHE 方案。 请查看 Craig Gentry 博士关于以下论文中 FHE 的论文:
https://crypto.stanford.edu/craig/craig-thesis.pdf
可悲的是,FHE 在性能和存储要求方面存在限制,并且仍在开发中。 你不可能拥有一切!
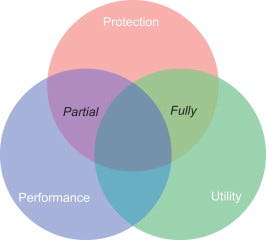
来自 Science Direct ( https://www.sciencedirect.com/topics/computer-science/fully-homomorphic-encryption)
开源同态加密
LattiGo
GitHub — tuneinsight/lattigo: A library for lattice-based homomorphic encryption in Go
Microsoft SEAL
Microsoft SEAL: Fast and Easy-to-Use Homomorphic Encryption Library
PALISADE
PALISADE / PALISADE Release · GitLab
HElib
GitHub — homenc/HElib: HElib is an open-source software library that implements homomorphic…
阈值签名 (TSS)
阈值签名 (TSS) 允许各方共享以数字方式签署消息的能力。
阈值签名需要一组授权的参与方(访问结构)代表该组生成签名。 只有当阈值(t out of n,t = 签名者的阈值,n = 签名者的总数)的签名者签署该消息时,该消息才被视为已签名。
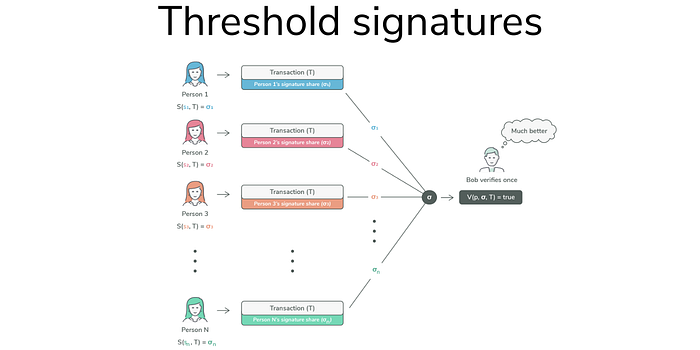
来源:https://blog.keep.network/threshold-ecdsa-safer-more-private-multi-signatures-51153f3e9ed2
阈值签名方案的示例有 El Gamal、Schnorr 和多重签名。 多重签名具有额外的功能,可以显示生成它们的小组成员的身份。
免费加入 Medium 以获取来自 该 作者的更新。
TSS 和 Shamir 秘密共享 (SSSS) 听起来很相似……
TSS 和 SSSS 相似,因为它们都需要小组中一定数量的参与者来协作处理秘密。 TSS 和 SSSS 之间的最大区别在于,中心化“经销商”处理秘密共享生成过程和重组。 在保护加密货币时,SSSS 中的“经销商”将生成所有密钥共享,将它们分发给所有不同的方,并在签名时在一个位置重新生成私钥。 使用 TSS,私钥永远不会在一个地方。
查看 Rosario Gennaro 关于阈值签名以及它们如何与 RSA 签名一起使用的讲座:
茫然传输 (OT)
在我们深入研究不同的协议之前,我们将回顾什么是茫然传输。相信我,当我们进入姚氏混淆电路协议时,所有这些都会联系起来。
茫然传输基于 Diffie Hellman 密钥交换协议*。 茫然传输允许发送者将两个秘密消息作为输入发送到 OT 机器,而不知道将接受哪个消息。 接收者将选择他们想要接收的消息,而不会让发送者知道
什么是 Diffie Hellman 密钥交换协议?*
Diffie Hellman 是一种端到端加密密钥交换方法,它允许双方通过为每一方提供足够的信息来获得相同的秘密而无需共享秘密来安全地通信。
现在让我们看看 Alice 和 Bob 关于茫然传输的故事……
Bob 生成 2 个 El Gamal 公钥,Alice 可以使用它们来加密她的两条消息。
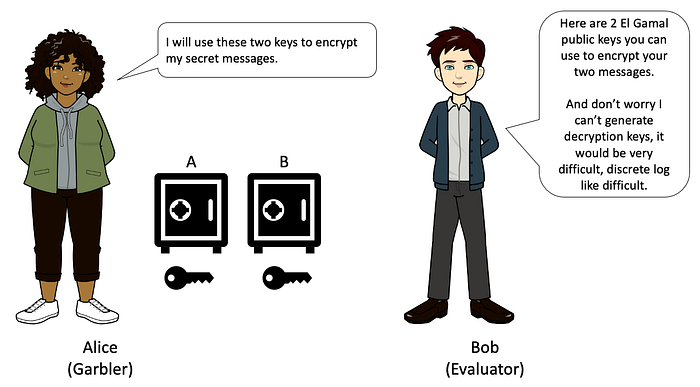
Alice 使用 Bob 发送过来的公钥加密她的两条消息,并将消息发送给 Bob。
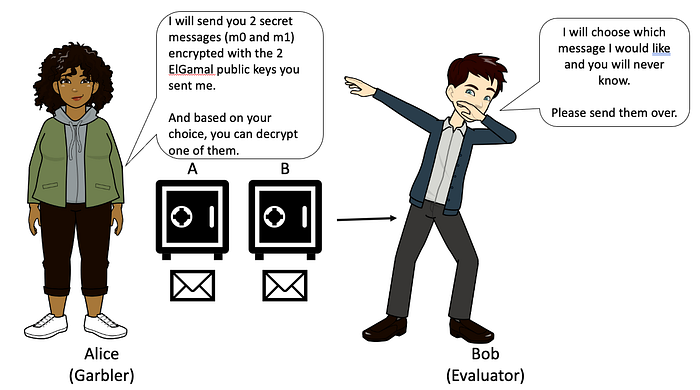
Bob 使用他的选择密钥来解密他所做的选择。 他将无法解密其他消息,并且 Alice 永远不会知道他的选择。
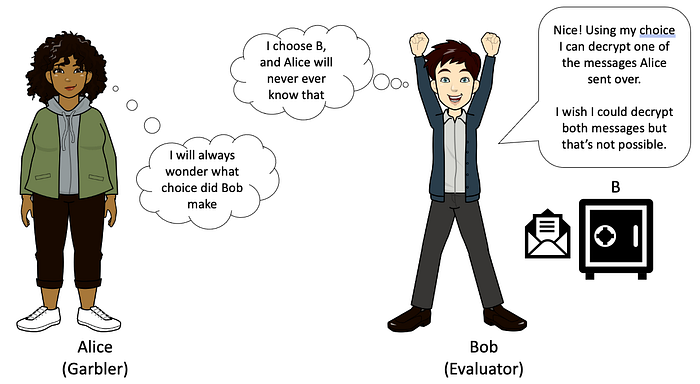
瞧! 这是高等茫然传输,请参阅以下资源以获得更深入的了解。
斯坦福大学关于茫然传输和混淆电路的讲座
以下是斯坦福大学关于茫然传输和混淆电路的讲座:
https://crypto.stanford.edu/cs355/18sp/lec6.pdf
ADI Engineering 上的 3 部分博客
Bill Buchanan OBE 教授 关于茫然传输的视频
不同的 MPC 实现
如今,有许多 MPC 算法在使用中,其中一些是姚氏协议、Gennaro & Goldfeder、Lindel、Doerner、MPC CMP 和 PSI(私有集交集)。
姚氏协议
姚氏协议是 MPC 最简单的形式,它引入了混淆电路。 它是为“诚实但好奇”(半诚实)的情况而构建的,在这种情况下,各方遵循协议来创建和评估电路,但在交换过程中可能会尝试学习额外的信息。 还有恶意情况或拜占庭对抗,此特定协议未考虑在内。
姚氏混淆电路协议如何工作?
姚氏协议使用“混淆器”和“评估器”解决两方隐私保护计算问题。 混淆器获取结果并像洗牌一样对它们进行混淆,评估器从洗牌后的输入中得出结果。
在开始有趣的事情之前,我们需要首先将我们需要评估的函数转换为门电路。
门
任何离散的、固定大小的函数都可以实现为逻辑门(与、或、非、异或等),并且可以表示为真值表。 查看 https://byjus.com/jee/basic-logic-gates/ 以更深入地研究门。
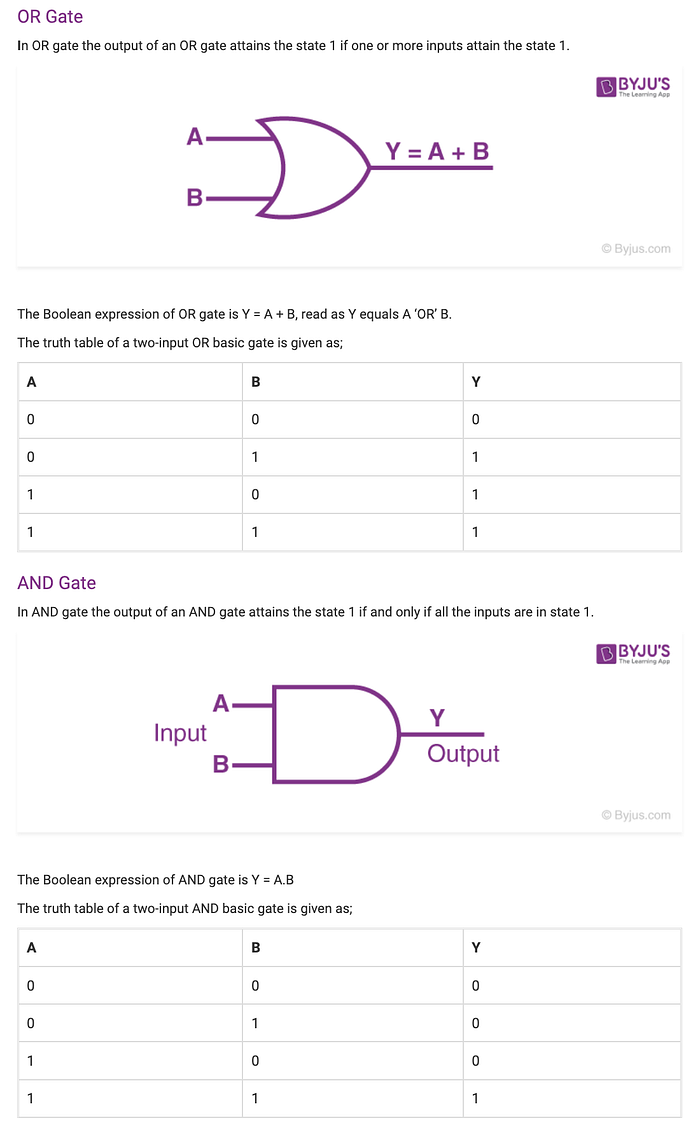
截图来自 https://byjus.com/jee/basic-logic-gates/
使用上面的图片,表达式 AB + BC + AC 在电路中看起来像下面的图片。
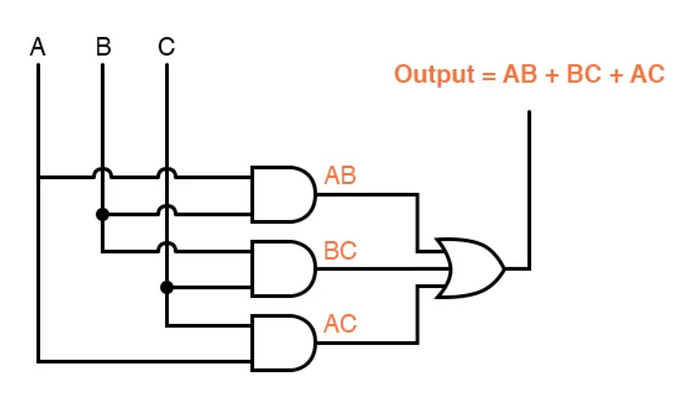
现在的目标是对电路进行加密,这样我们就不会知道电路的输入和输出,并且仍然生成一个可以用作下一个门电路的输入的输出。
混淆电路
加密电路的真值表称为“混淆电路”。 在混淆电路中,我们有一个评估器和一个混淆器,名称说明了一切,混淆器是对电路进行混淆的人,评估器是评估电路的人。 以下是关于混淆电路的故事:
Alice 通过将她的函数转换为电路来创建她的“真值表”
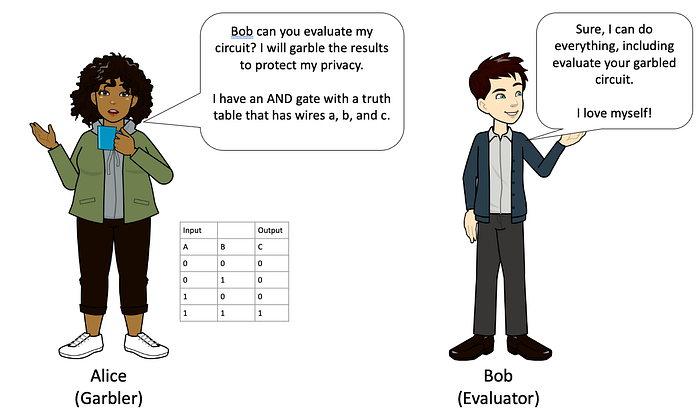
Alice 混淆了她的真值表并加密了她的输出密钥
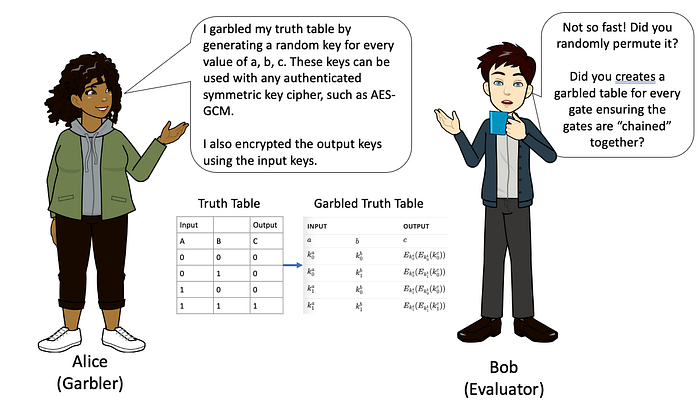
Alice 发送了混淆电路和她的加密密钥,现在 Bob 几乎准备好进行评估了
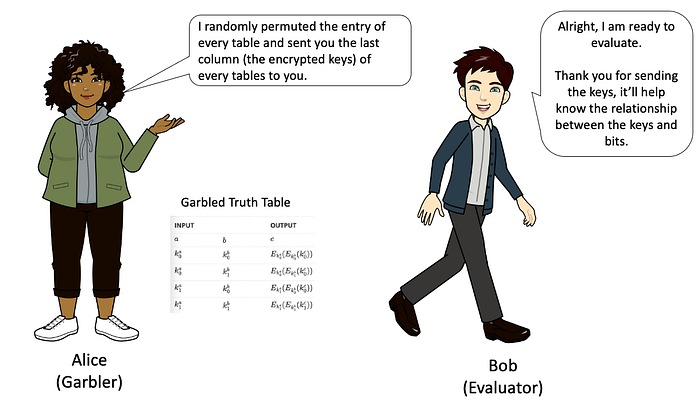
Alice 要求 Bob 将他的密钥发送给她
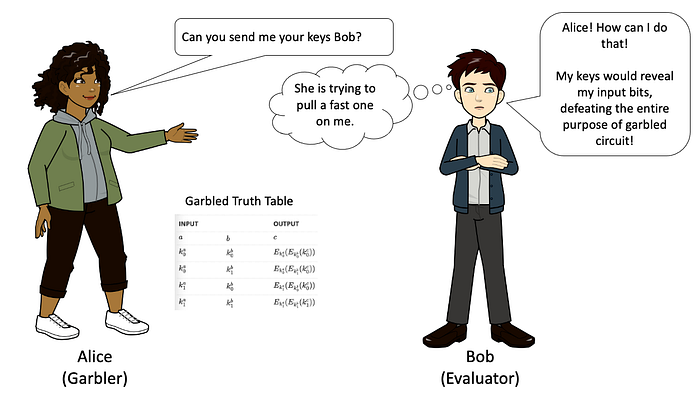
Bob 无法发送他的密钥,因此 Alice 建议使用茫然传输
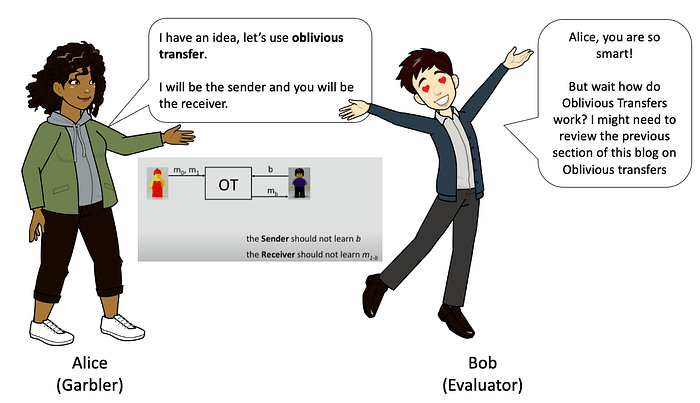
查看 Ku Leuven Cosic 研究中心对混淆电路的介绍:
https://www.esat.kuleuven.be/cosic/blog/introduction-to-garbled-circuit/
PSI(私有集交集)
我们中的许多人已经与 Google 实施的 MPC 进行了交互。 当 Google Chrome 通知你你的密码已泄露时,他们会使用 MPC,特别是 PSI。
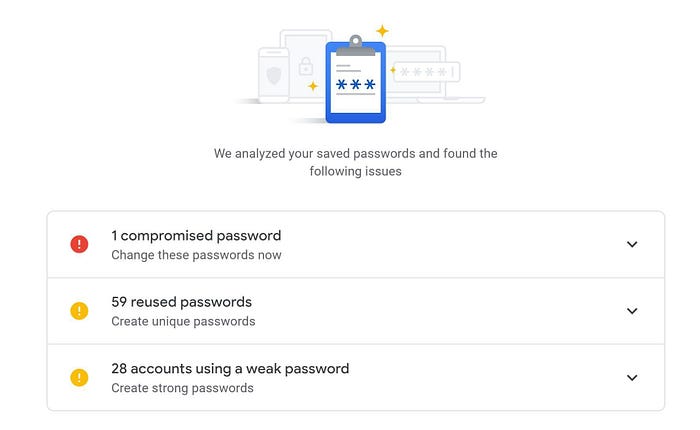
他们没有读取你的密码。 相反,他们使用的是 MPC 实施:私有连接和计算, 他们正在将你的加密密码与泄露密码的加密列表进行交叉引用。
以下是 Google 关于 PSI 的一个很好的视频:
此信息图澄清了 MPC 中的一些困难概念:
https://storage.googleapis.com/gweb-uniblog-publish-prod/documents/private_join_and_compute.pdf
MPC CMP(UC 非交互式、主动式、阈值 ECDSA)
MPC CMP 基于 Gennaro(纽约城市学院)和 Goldfeder(康奈尔大学)以及 Lindell 和 Nof 协议。 它由 Ran Canetti(波士顿大学)、Nikolaos Makriyannis (Fireblocks) 和 Udi Peled (Fireblocks) 设计。 MPC CMP 解决了以下问题:
- 减少签名轮数(性能): 签名生成需要 4 轮,而以前需要 8 轮。
- 非交互式(冷钱包支持): 3 个签名生成轮数在已知签名消息之前在预处理中完成,从而允许非交互式属性,其中并非所有机器都需要同时联机。
- 可识别中止(问责制): 如果发生故障,则会识别出有缺陷/恶意的签名者。
- 主动安全(自适应对抗安全): 保护针对自适应对抗者的长期安全。 自适应对抗者是允许动态演变的对抗者,有自适应在线对抗者(中等对抗者)和自适应离线对抗者(强大对抗者)。
- UC(通用可组合)安全: 它使用 UC 框架进行全局随机预言模型、强大的 RSA、Paillier 加密的语义安全以及 ECDSA 的增强型存在 不可伪造性。
关于轮数的说明
各方在一系列轮次中交换信息,以计算给定消息的签名。 由于 CMP 利用 pallier 加密作为承诺方案,因此它可以降低轮数复杂性并支持并发签名。
pallier 承诺和 ZK(零知识)证明的结合使各方能够确信共享在预签名阶段结束时形式良好,这意味着不需要额外的轮数。
在线和离线签名轮数
CMP 交互式(在线签名)要求各方运行预签名阶段,然后是签名阶段,总共 4 轮。 非交互式(离线签名)的不同之处在于签名 nonce 在消息签名之前已知。 为了证明安全性,我们依赖于关于底层(非阈值)方案的不可伪造性的假设。
以下是 MPC CMP 和其他 MPC 算法之间的比较:
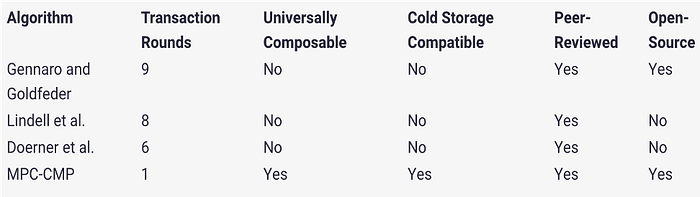
查看白皮书以了解有关该实施的更多详细信息:
或者查看介绍视频:
或详细视频:
如果你喜欢这篇文章,你可以给我买咖啡,提前谢谢你!
感兴趣了?了解有关 MPC 的更多信息
ZenGo 的 MPC 介绍视频 — 相亲游戏
ZenGo 的 2020 年 MPC 预测
MPC 联盟
Pragmatic MPC — PDF 书籍
https://www.cs.virginia.edu/~evans/pragmaticmpc/pragmaticmpc.pdf
MPC Awesome
GitHub - rdragos/awesome-mpc: A curated list of multi party computation resources and links.
Meta 的 MPC 介绍
Nigel Smart 的多方计算:从理论到实践的演示
FastAPI 在哪里变成 FastEnclaves:几分钟内的 MPC 🦹♀️ 🦸♂️ 👩🚀
GitHub - ObliviousAI/FastAPI-Enclave-Services: This is the home of FastAPI for enclave…
Yehuda 的安全多方计算
- 原文链接: medium.com/coinmonks/sec...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Uniswap Labs Compact Emissary代码审计 342 浏览
- 哈希方法的构建者(以及更多) 409 浏览
- Plinko PIR 教程 635 浏览
- 为什么数字投票系统(真正有效的)用了这么长时间才实现 1310 浏览
- B-SSL:一种无需限制条款的保险柜合约架构 995 浏览
- 永久隐私投票即将登陆 Snapshot 654 浏览
- 多签名钱包什么时候要更换密钥? 849 浏览
- B-SSL:比特币安全签名层 441 浏览
- 多签名钱包使用习惯常见误区及其纠正 1087 浏览
- HPU深入解析:同态加密运算如何在同态处理器上运行 1387 浏览
- TFHE-hpu-backend - 用于连接HPU加速器 1068 浏览
- 密码学之 Ecdsa 签名、GG20、MPC 钱包 (四) 完整版 1217 浏览


