聚合签名、阈值签名、多重签名及多重签名
- ramsesfv
- 发布于 2022-04-01 12:49
- 阅读 907
本文对多重签名、聚合签名和阈值签名进行了比较,重点介绍了MuSig2和FROST两种方案。多重签名简单但效率较低,聚合签名提高了效率但较为 rigid,阈值签名则更为灵活。MuSig2通过密钥聚合和两轮签名实现高效多重签名,FROST则采用分布式密钥生成和半信任签名聚合器实现阈值签名。
简要调查与比较

简介
数字签名在区块链技术中起着核心作用,因为每笔交易都需要签名才能生效。 确切地说,数字签名在区块链协议中具有三重目标:
- 它们证明所有权并提供支出资金的授权。
- 它们证明不可否认性,意味着授权证明是不可否认的。
- 它们证明交易尚未且无法被修改。
当前的签名方案,其中单个用户为消息颁发签名,可能会受到潜在威胁,因为它代表一个单点故障,如果恶意用户控制了密钥,可能会破坏该方案。
上述问题可以通过引入多重签名方案或阈值签名来避免。 这两种方案非常相似,因为它们都是多方协议,并且需要 至少 m 个(共 n 个)用户签署文件以证明真实性。 然而,它们之间存在一些重要差异,本报告的目的是从较高层面比较这两种签名方案。
由于该领域正变得活跃,涌现出 MuSig2 或 FROST 等多个提案,现在是介绍和比较三种技术的好时机,这些技术具有一些相似之处和不同之处,并且在区块链环境中容易被混淆。 目标是介绍多重签名、阈值签名和聚合签名,尽可能避免任何技术术语,同时简单介绍 MuSig2 和 FROST。
数字签名方案
以下部分可能存在争议,因为其中一个目标是消除围绕多重签名、阈值和聚合签名等概念的混淆,这些概念在区块链中的许多情况下会合并和组合。
多重签名
在多重签名的朴素方法中,n 个用户中的每一个都有一对公钥/私钥。 在这种情况下,有效的签名是 n 个用户的签名集合。 签名的验证需要使用每个签名者的公钥来验证最终签名。
允许每个参与者拥有自己的密钥对使得基于多重签名的身份验证占用更多空间。 需要 至少 n 个签名的配置不仅必须包含所有 n 个签名,还必须包含 n 个公钥。 这使得多重签名交易的成本更高,空间和处理成本与 n 成线性关系。
另一方面,拥有个人密钥对的用户有机会并行参与多个签名过程,这与阈值签名不同,在阈值签名中,每个参与者都有一个共享密钥,该密钥颁发签名的 一部分。 这些份额必须组合起来才能生成有效的最终签名。 请注意,这些份额本身不能用于另一个签名过程中。
多重签名方案中涉及的密钥存储在 链上,而在阈值方案中,计算和密钥共享是在 链下 执行的,并且只有 一个 公钥存储在链上。 这使得阈值方案在验证所需的空间和计算方面比多重签名提案便宜得多。
由于效率低下,朴素的多重签名可能不是区块链的最佳解决方案。 为了克服这个问题,一些解决方案允许参与该过程的所有参与者使用他们的私钥对消息进行签名; 然后将输出组合成一条消息,该消息使用组合公钥进行验证。 例如,MuSig2 使用的就是这种机制,如下所述。
聚合签名
聚合签名用于减少证书链的大小或减少路由协议中的消息大小等应用。
聚合签名是多重签名的非平凡推广(其中所有用户签署相同的消息)。 聚合签名允许从来自 m 个不同签名者的 m 条不同消息上的签名创建单个紧凑签名。这提供了更快的验证以及存储和带宽的减少。
有两种主要的签名聚合机制:通用聚合和顺序聚合。 为了描述这些机制,假设一组 m 个用户,每个用户都有一对公钥/私钥,并且用户 i 想要签署消息 Mi。
- 在通用签名聚合方案中,每个用户 i(来自 m 个用户的组)在他的消息 Mi 上创建签名 i。 为了生成聚合签名,任何人都可以运行公共聚合算法来获取所有 m 个签名(σ1, σ2, …, σk)并将它们压缩为单个签名 σ。
- 在顺序签名聚合方案中,用户 1 签署 M1 以获得 σ1; 然后用户 2 组合 σ1 和 M2 以获得 σ2; 依此类推。 最终签名 σ 由用户 k 生成,该用户绑定 Mk 和签名 σk-1。 顺序签名聚合只能在签名过程中发生。
用于聚合签名的技术对于各种签名方案都是已知的,例如 Schnorr、基于格的和基于配对的签名方案。 关于基于配对的聚合签名,重要的是要强调 BLS 方案(Boneh 等人),该方案正被诸如 Dfinity 和 Algorand 等区块链提案使用。 然而,这些提案签署的是 相同的消息,因此人们应该将这些解决方案视为多重签名的一个例子,而不是适当的聚合签名方案。
最后但并非最不重要的一点是,大多数提案在签署消息时都需要特定的顺序,但是有些方案不再需要此要求(Lu 等人)。
聚合签名方案应限制任何对手自行创建有效的聚合签名。
阈值签名
(m, n)-阈值签名方案是一种数字签名方案,其中来自 n 个签名者组中的任何 m 个或更多签名者可以代表该组生成签名。 然后可以使用 公共组密钥 验证此签名,该密钥是在组合参与者的公钥后生成的。 通常,阈值签名不会泄露已合作生成它的实际组成员。
阈值签名方案的目标是(对于 m > 1)强制控制签名能力,(对于 n > 1)消除单点故障,或两者兼而有之。
每个签名者组可以由受信任的组机构管理,该机构负责监督加入和离开该组。 许多组可以选择由同一受信任的组机构管理,或者一个组可以选择在其成员之间完全分配组管理,以便每个成员都参与所有管理操作。
组 G 的(超过)m 个成员中的任何子集都可以生成签名。 为此,每个成员将部分签名贡献给指定的组合器,并且组合器从部分签名派生出预期的阈值签名。
每个有权访问组 G 的公共组密钥的人都可以验证阈值签名。 指定的组合器可以是真实实体,例如受信任的组机构,也可以是虚拟实体,其操作在所有组成员之间以分布式方式计算。 如果指定的组合器可以在接受每个部分签名作为阈值签名的输入之前验证其有效性,则阈值签名方案是可靠的。
一个比较
到目前为止,我们已经描述了四种彼此非常相似的技术。 以下是对所调查的几种方法的比较:
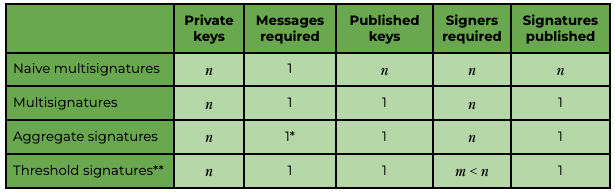
(*) 在这种情况下,消息可以是不同的,最多 n.
(**) 假设为 (m, n) - 阈值方案。
MuSig2 和 FROST 简介
在正在考虑在区块链平台中引入多重签名或阈值签名的提案中,发现了 MuSig2 和 FROST。 以下部分旨在作为对这两种方案的简要、非技术性介绍。 那些对细节和数学基础感兴趣的人会喜欢阅读(Nick 等人)和(Komlo 和 Goldberg)。
MuSig2 简要介绍
MuSig2(Nick 等人)提案不能被认为是朴素的多重签名方案,因为它与聚合签名提案有一些相似之处。
在该方案的亮点中,可以发现:
- 它在并行签名会话下是安全的。
- 密钥聚合的可能性。
- 它输出普通的 Schnorr 签名。
- 与早期需要三轮的 MuSig 提案相比,它将通信轮数减少到两轮。
- 签名者复杂度类似于普通 Schnorr 签名。
在 MuSig2 中,每个参与者都有一对密钥,一个私钥和一个公钥。 它们是通过随机取 x ∈ ℤ 并计算 X = g^x 来生成的,其中 g 是循环群 G 的生成器。
该方案使用两轮签名来为 m 个用户生成 m 个中间签名,并且这些签名的最终组合会创建一个最终签名。
使用由用户公钥组合生成的公钥来验证此签名。
当此方案用于验证区块链交易时,链上发布的唯一数据是一个公钥和一个签名,这与通常的 Schnorr 签名无法区分,因此成本远低于多重签名,并且等于阈值机制生成的成本。 此外,MuSig2 中的密钥生成比阈值方案中的密钥生成更简单。 与任何阈值签名方案相比,MuSig2 的主要缺点是它需要 m 个签名者参与 (m = n),这使得 MuSig2 成为一个刚性的解决方案。
将多重签名转换为阈值方案
为了使多重签名更灵活,可能的解决方案可能是修改算法以将其转换为阈值方案。 此选项需要定义一个包含所有可接受签名者的密钥的 Merkle 树。 此 Merkle 树将允许通过遍历它来检查一组潜在签名者是否有效。

令 n 为参与者的数量,m 为阈值。 上述 Merkle 树中包含的元素数量是组合数 C(n,m)。 这棵树的空间复杂度 O(n^(n-m)) 在阈值上呈指数级增长。
在 Merkle 树中搜索、遍历、插入或删除元素的时间复杂度为 O(log(C(n, m)))<O(log(n^m))=O(m · log(n))
包含具有可接受签名者组的 Merkle 树的想法可以与 MuSig2、BLS 或任何其他多重签名方案一起使用。 此功能包含在 Taproot 中,位于 merkelized abstract syntax trees ( MAST) 的底层,这是一种使用 Merkle 树存储必须满足的各种用户选择条件的方法,以便花费受约束的比特币。
FROST 简要介绍
阈值提案 FROST(Komlo 和 Goldberg)使用半信任签名聚合器 (SA),其角色允许签名者减少网络开销。 聚合器用于协调,并且它无权访问特权信息。 SA 角色可以由协议的参与者或外部第三方扮演。 SA 被信任以识别行为不端的参与者,并且还负责在协议结束时发布组的签名。 如果 SA 行为不端,该协议仍然可以防御自适应 CCA。 恶意 SA 有权执行 DDoS 攻击,或错误地报告恶意参与者,但无法学习私钥或导致签署不正确的消息。
FROST 中的密钥生成分两轮完成,并依赖于 Pedersen 的分布式密钥生成算法,而签名算法建立在加法秘密共享之上。
此外,签名操作使用绑定技术来避免伪造攻击。 签名过程包括两个部分:预处理阶段和单轮签名阶段,但是可以将它们组合起来以获得单轮签名阶段。
最后的想法
到目前为止研究的不同技术都具有优点和缺点。 由于需要验证不同的签名,因此可以认为朴素的多重签名效率低下。 然而,这是最简单的解决方案,并且取决于参与者的数量,这可能是一个有趣的选择。
具有聚合属性的多重签名方案(例如 MuSig2 或 BLS)克服了上述效率问题,因此当参与者数量增加时,可以将其视为可行的解决方案。 然而,严格来说,多重签名(无论是朴素的还是非朴素的)仍然有点僵化,因为它要求参与操作的所有参与者都必须在场。
更灵活的解决方案是考虑阈值方案,无论是实施基于分布式密钥生成的方案(例如 FROST 或 Stinson 和 Strobl 提出的方案 (Stinson and Strobl)),还是将包含可接受签名者的 Merkle 树与任何多重签名提案(例如 MuSig2 或 BLS)结合使用。
参考文献
- Boneh, Dan, et al. “来自双线性映射的聚合和可验证加密签名。” Lecture Notes in Computer Science, vol. 2656, Springer, 2003, pp. 416–432. SpringerLink, https://link.springer.com/chapter/10.1007/3-540-39200-9_26.
- Komlo, Chelsea, and Ian Goldberg. “FROST:灵活的轮优化 Schnorr 阈值签名。” Lecture Notes in Computer Science, vol. 12804, Springer, 2021, pp. 34–65. SpringerLink, https://link.springer.com/chapter/10.1007/978-3-030-81652-0_2.
- Lu, Xiuhua, et al. “一种基于交集法的基于格的无序聚合签名方案。” IEEE Access, vol. 6, 2018, pp. 33986–33994. IEEE Xplore, https://ieeexplore.ieee.org/document/8386429.
- Nick, Jonas, et al. “MuSig2:简单的两轮 Schnorr 多重签名。” Lecture Notes in Computer Science, vol. 12825, Springer, 2021, pp. 189–221. SpringerLink, https://link.springer.com/chapter/10.1007/978-3-030-84242-0_8.
- Stinson, Douglas R., and Reto Strobl. “可证明安全的分布式 Schnorr 签名和用于隐式证书的 (t, n) 阈值方案。” Lecture Notes in Computer Science, vol. 2119, Springer, 2001, pp. 417–434. SpringerLink, https://link.springer.com/chapter/10.1007/3-540-47719-5_33.
- 原文链接: medium.com/iovlabs-innov...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- DahLIAS:既非 ECDSA,也非 Schnorr 234 浏览
- FROST 的关键一步:何为分布式密钥生成? 605 浏览
- 门限方案攻击:第二部分 368 浏览
- Web3 安全指南 697 浏览
- 警惕 Solana 钓鱼攻击:钱包 Owner 权限可能被篡改 515 浏览
- “天才实习生”问题:为什么区块链是唯一足够强大的手铐,可以约束…… 407 浏览
- 链码委托:比特币密钥的隐秘访问控制 1184 浏览
- 隐私账户的智能合约或EOA花费授权 427 浏览
- BlockThreat 周报 - 2025 年第 44 周 710 浏览
- 多签名钱包使用习惯常见误区及其纠正 1077 浏览
- BlockThreat - 2025年第39周 1083 浏览
- 密码学之 Ecdsa 签名、GG20、MPC 钱包 (四) 完整版 1191 浏览

