椭圆曲线与离散对数问题

两周前，我开始阅读 Jimmy Song 的《Programming Bitcoin》，目标是构建一个实用程序库，同时进行学习。前几章介绍了非对称密码方案——椭圆曲线密码学 (ECC)——比特币使用的基本数学原理。这是一个基于有限域上的椭圆曲线的密码系统，其中随机选择的私钥用于轻松生成公钥，但反之在计算上是困难/不可能的。

但是什么是椭圆曲线？什么是有限域？为什么比特币使用 ECC？

椭圆曲线

为了回答这些问题，我需要更好地理解 ECC 中使用的基础数学。在本文中，我总结了所学到的关于以下内容：椭圆曲线、有限域、群、群律以及有限循环群、离散对数问题 (DLP) 和椭圆曲线离散对数问题 (ECDLP)。

椭圆曲线

考虑描述椭圆曲线的等式的一种方法是考虑一堆橘子，这些橘子的排列方式是每一层都包含一个橘子的正方形矩阵，形成一个金字塔。例如，堆栈底部第 4 层的包含 (4 x 4) = 16 个橘子，第 3 层包含 (3 x 3) = 9 个橘子，Layer2有 (2 x 2) = 4 个橘子，Layer1 (1 x 1) = 1 个橘子。考虑一个有趣的问题，将 n 层的橘子堆栈重新排列成一个单一的正方形矩阵。如果堆栈中有 3 层，是否可以得到一个正方形矩阵？为了找出这是否可能，我们必须对每一层的平方求和，然后计算平方根。如果平方根是整数，那么我们就找到了一个解。

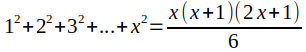
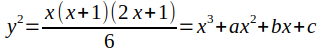
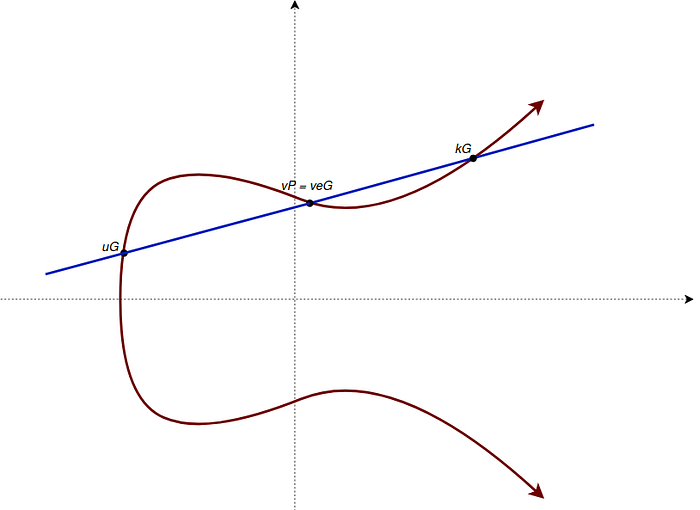
上面的等式表示一个椭圆曲线。在知道曲线上两个点的情况下，第三个点可以通过椭圆曲线与穿过两个已知点的直线的交点找到。

为什么这个方程以及找到它的解很重要？要回答这个问题，我们必须了解什么是有限域和群。

有限域

如果一个事物具有可定义/确定的界限，那么它就被认为是有限的。因此，有限域是任何具有有限元素集合的域（数的抽象）。这意味着在表示集合大小/阶的集合中存在可数数量的元素。有限域还具有数学运算（加法和乘法），可以对集合中的元素执行这些运算，使得这些运算的结果是封闭的，即在集合中。以下对于有限域必须为真：

1. 这些运算符，加法（+）和乘法（.），执行二元运算
2. 元素 c 和 d 相加的结果必须在集合中，使得加法是封闭的。
3. 存在一个中性元素 0，使得 0 + c = c
4. 存在单位元素 1，使得 1.c = c
5. 存在 -c，使得 -c + c = 0
6. 存在 c 的逆元，使得

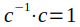
7. 存在 素域，其中有限域的阶是一个素数 p，该域中集合的元素（mod p）是 {0, 1, 2, …, p — 1}

这些条件成立是因为模运算允许超大的结果绕除数折回，余数落在除数定义的边界内。下面的代码片段展示了如何在 Python 中实现有限域元素。

# 有限域元素 Python 实现

群、群律和循环群

有限域和该域上的椭圆曲线的组合产生了一个有趣的实体——群。如果你有一个有限域和一个定义在该域上的椭圆曲线，使得曲线上两点相加的规则导致第三个点在同一曲线上，那么我们就得到了一个群。

群通常有一个定律，即点加法（+），它扩展了有限域运算的必要条件。这些条件是：

加法单位元：给定椭圆曲线上的一个点 P(x,y)，存在一个单位元素 0(x,y)，使得 0 + P = P. 这个单位元素被称为无穷远点。

加法逆元：给定曲线上的一个点 P(x,y)，存在另一个点 P(x,-y)，使得 - P + P = 0 .

点加法：给定椭圆曲线上的两个点 P₁(x₁, y₁) 和 P₂(x₂, y₂)，第三个点 P ₃ (x ₃ , y ₃ ) 的计算方法是计算通过 P₁ 和 P₂ 的斜率（m），并将其代入通过 P₁ 或 P₂ 和 P ₃ 的直线方程。这些方程如下所示，并且对于 P₁ 不是 P₂ 的情况成立。

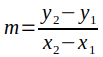
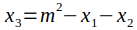
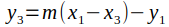
点倍乘：当 P₁ = P₂ 时，会发生倍乘。这里 P₁ + P₂ = P₁ + P₁ = 2P₁. 形成的线与点 P₂ 相切，并通过第三个（技术上是第二个）点。这条线的斜率是通过取椭圆曲线方程的导数来找到的。计算 y ₃ 的方程保持不变，但是，斜率和 x ₃ 方程会发生变化，如下所示。

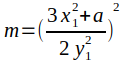
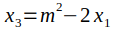
标量乘法：点倍乘向我们展示的是，我们可以执行一种新的运算，称为标量乘法，其中 P + P = 2P，而 2 是一个标量倍数。这个属性是非线性的，并引发了两个重要的考虑因素：有限循环群和离散对数问题。

有限循环群：

在选择的 P 的某个标量倍数（n）处，我们计算无穷远点 nP = 0。对于选择的 P，这意味着存在一个有限的 P 的倍数集合，称为有限循环群。并且 {P, 2P, 3P, 4P, …, nP} 在有限域上的图是一系列散点，显示了有限循环群中点加法的非线性。这种非线性是密码系统中的一个很好的属性，因为计算选择的点的标量倍数很容易，但是给定一个点来预测标量的值却非常困难。这就是离散对数问题 (DLP)。

简化的椭圆曲线 y² = x³ + ax + b 上的点可以在 Python 中实现，如下所示。

离散对数问题

有限域中的广义离散对数问题定义了在 1 和 p — 1 范围内找到整数 x 的难度，如果存在：

1. 一个阶数为 p — 1 的有限循环群
2. 一个属于有限循环群的本原元素（α）
3. 一个导数元素（β），使得 αˣ = β

如果参数（p, α, β）足够大，则计算 x 的值非常困难，即使计算 β 的值要容易得多。

扩展来说，可以使用椭圆曲线构造一个 DLP。形式上，椭圆曲线离散对数问题 (ECDLP) 是找到一个整数值 e，该值在 1 和椭圆曲线上的点数（其 ~= 有限循环群的阶）的范围内，使得本原元素 G 与 e 的标量乘法，即 eG, 产生椭圆曲线上的另一个点 P。

在密码系统中，e 表示统一选择的随机数，即私钥，G 表示生成器点，P 表示导出的公钥。

将它们结合在一起

椭圆曲线和 DLP 很重要，因为它们构成了 ECC 的原语。对于有限循环群的阶数（n）、生成器点（G）和有限域的阶数（p）的足够大的值，可以实现椭圆曲线离散对数问题，以用于安全和注重隐私的系统。比特币使用的值（参见《Programming Bitcoin》第 3 章，第 59 页）足够大，不会受到成功的攻击，并且已知可以提供长达数十年的长期安全性。

与同一非对称算法家族中的方案相比，ECC 以显着更小的密钥长度提供了相同的安全级别。例如，为了达到 128 位的安全级别，ECC 需要 256 位的密钥长度，而 3072 位是其他方案中相同安全级别的最低要求。处理 256 位的密钥长度比 3072 位密钥的实用性更高，速度也更快。

注意：

1. 如果你对 Python 中字段和群运算的实现感兴趣，这里是指向《Programming Bitcoin》代码库的链接。 C++ 中的实现包含在《Pro Cryptography and Cryptanalysis》的第 9 章中。
2. 如果上面的资源太详尽，你可以查看我的 存储库。它占用的空间要小得多，并且包含与从《Programming Bitcoin》学习一起编写的代码。

参考文献

1. Song, J. (2019). Programming bitcoin: Learn how to program bitcoin from scratch O’Reilly Media.
2. Hankerson, D., Menezes, A., & Vanstone, S. (2004). Guide to elliptic curve cryptography Springer.
3. Paar, C., & Pelzl, J. (2010). Understanding cryptography (2. corr. printing ed.). Springer.
4. Mihailescu, M., Iulian, & Nita, S., Loredana. (2021). Pro cryptography and cryptanalysis with C++20: Creating and programming advanced algorithms Apress.

• 原文链接： enigbe.medium.com/about-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～