ZK约束系统的形式化验证

由 Morgan Thomas 和 Ventali Tan 撰写

感谢 Kestrel Institute 的 Eric McCarthy 在本文档的某些章节提供的帮助，以及 Grigore Rosu (UIUC)、Shashank Agrawal (Delendum)、Daniel Lubarov (Delendum)、Tim Carstens (Risc Zero)、Bolton Bailey (UIUC)、Alessandro Coglio (Kestrel) 和 Mikerah 提供的许多有益建议。

主要问题

我们如何形式化验证一个算术电路（正如 零知识证明系统 所使用的）具有所需的特性，例如可靠性、完备性和零知识性¹？

证明系统的可靠性意味着它不会证明错误的陈述。类似地，证明系统所使用的电路的可靠性意味着这些电路在应用于不真实的陈述时是不可满足的。

证明系统的完备性意味着它能够证明所有真实的陈述。类似地，证明系统所使用的电路的完备性意味着该电路在应用于真实的陈述时是可满足的。

电路的可靠性和完备性加在一起，等同于电路所表示的关系是预期关系这一陈述。

一个证明系统是零知识的，当且仅当一个证明没有揭示任何超出被证明陈述（即，证明过程的公共输入）的额外信息。任何被证明的陈述直接暗示的事实必然也被证明所暗示，但不应揭示未被陈述暗示的额外事实。额外的“非公共”见证数据（可以被视为秘密输入）不得被揭示。

一个可靠且完备的电路只能被在预期语义中为真的陈述所满足。如果底层证明系统是可靠且完备的，并且如果电路是正确的，那么整个系统提供了一种证明预期陈述的可靠且完备的方法。我们可以将主要问题分解为两个子问题：验证底层证明系统的所需特性，以及验证电路的可靠性和完备性。换句话说，电路表示预期关系，并且证明系统在应用于电路时将按预期运行。

我们这里的主要重点是第二个子问题，即验证系统的电路，同时假设底层证明系统的可靠性和完备性。

零知识证明系统经常使用数学约束系统（如 R1CS 或 AIR）来编码计算。零知识证明是一种概率密码学证明，证明计算完成正确。对零知识证明中使用的电路进行形式化验证需要（1）电路旨在编码的关系的形式化规范，（2）电路语义的形式化模型，（3）电路本身，（4）定理证明器，以及（5）关于（1）、（2）和（3）之间关系的定理的机械化证明。

技术

要确定地证明一个通用陈述，它必须是一个纯粹的数学陈述，可以通过仅仅推理来知道它是真的，而不需要执行任何测试。推理必须从一致的假设（公理）开始，并通过保持真理的推论进行。

• 例子：给定单身汉被定义为未婚男子，而已婚男子根据定义有配偶，因此可以确定地证明没有单身汉有配偶。

一种证明理论（有时也称为逻辑或元逻辑）编纂了一套一致的规则，用于执行保持真理的推论。证明理论可以用来手动构造证明，用笔和纸。

• 例子：经典逻辑的相继式演算

被称为证明助手的计算机程序通过帮助用户构造机器可检查的证明来减少劳动并降低人为错误的风险。

• 例子：Coq、Agda、Isabelle、ACL2、PVS、Imandra 和 Lean

使用证明助手

要使用证明助手来证明关于程序的陈述，有两种主要方法：

1. 用证明助手语言编写程序，并将证明工具直接应用于该程序。
2. 使用转译器² 将用另一种语言编写的程序转换为证明助手可以推理的对象。这称为事后验证。

在这些方法中，（1）似乎更可取，因为证明是关于正在执行的（源）程序的确切证明，而不是转译器的输出，而后者被假定为与源程序具有相同的含义，从而提供了更大的信心。

当（由于任何原因）证明助手语言不适合作为开发应用程序的语言时，会激发方法（2）。

不使用证明助手

也有一些方法可以在不（直接）使用证明助手的情况下证明关于程序的陈述：

• 使用经过验证的编译器（例如CompCert），它将源程序转换为通过关于经过验证的编译器的（已证明的）事实而可以证明具有某些属性的对象程序。

请注意，经过验证的编译器和验证编译器之间存在区别。CompCert 本身被证明可以生成始终在语义上等效于 C 输入的二进制文件。一个验证编译器生成一个二进制文件，以及一个正确性证明，证明该二进制文件在语义上等效于源代码。

当程序由验证或经过验证的编译器编译时，我们说编译器输出通过构造是正确的（前提是输入是正确的）。

经过验证的编译器不会检测或修复输入源代码中的错误；但是，它们也不会在编译期间引入任何新错误。

• 使用自动证明搜索算法，该算法将要证明的陈述作为输入，如果这些陈述为真并且证明搜索算法找到证明，则输出这些陈述的证明。
• 使用静态分析器，它将程序作为输入，并使用预定的算法自动检查各种类型的问题。

所有这些方法都有局限性：

• 经过验证的编译器可以证明关于结果程序的哪些陈述是有限的：通常，只是结果程序与源程序具有相同的含义或行为。
• 自动证明搜索算法可以证明的陈述受到算法的复杂性和应用于它的计算能力的限制。此外，由于一阶算术的不可判定性，不可能存在一种证明搜索算法，可以找到任何给定真陈述的证明。
• 静态分析器通常无法推理程序的功能来查看它是否正确；它只能识别总是或经常表明某种问题的模式。

ZK 电路的形式化验证

概率证明系统（包括 ZK 证明系统）的形式化验证包括两个主要问题领域：

• 证明通用证明系统（例如，Bulletproofs、Halo 2 等）的预期属性，例如可靠性、完整性和零知识性。
• 证明电路的预期属性，即它正确地编码了预期的关系。

问题（1）通常被认为是一个非常困难的问题，并且尚未针对任何重要的证明系统完成。

问题（2）可以使用关系的形式化规范和电路语义的模型来完成。通常，它需要证明关系中定义的功能的功能正确性，以及每个函数参数的见证变量的存在。

请注意，有不同的方式来公理化一个问题以证明它。一些类别是指称语义、公理语义和操作语义。

_操作语义对于证明程序的属性特别有用。例如，在 ACL2 定理证明器中，形式化编程语言语义的常用方法是解释性操作语义，即用定理证明器的逻辑编写的高级解释器，它形式化了计算状态的可能形式，并描述了编程语言的构造（例如表达式和语句）如何操作计算状态。_

指称设计

指称设计为思考一般和特定应用问题空间提供了一种有用的方式。

指称设计提供了一种方法论，用于定义系统（例如零知识证明系统）的需求，以便可以在形式系统中表达和证明需求。

电路表示一个集合：即，电路可满足的公共输入（即陈述）的集合（即，该陈述为真）。

例如，考虑一个哈希验证电路：

• 公共输入是一个对 (x, h)，其中 x 是一些数据，h 是一个哈希值
• 公共输入 (x, h) 表示 h 是 x 的哈希值的陈述
• 当且仅当 h 是 x 的哈希值时，电路才能满足（或者应该是可满足的）

电路验证的目标是证明电路表示预期的关系。

通用证明系统验证的目标是证明它在电路的指称语义方面具有预期的属性：

• 可靠性意味着如果验证者接受了一个证明，那么以高概率，用于生成证明的公共输入（即，被证明的陈述）位于电路表示的集合中（即，该陈述为真）。
• 完备性意味着如果公共输入（即，一个陈述）位于电路表示的集合中（即，该陈述为真），那么证明算法成功地输出了一个验证者接受的证明。
• 例子：考虑一个 ZK 证明系统，人们可以用它来证明他有一个数独难题的解决方案，而不透露解决方案。
  • 要证明的陈述形式为“X（一个数独难题）是可解的”。
  • 我们打算的关系是可解的数独难题的集合。
  • 可靠性意味着如果验证者接受了 X 是可解的的证明，那么以高概率，X 是可解的。
  • 完备性意味着如果 X 是可解的的，那么证明者创建一个 X 是可解的证明，并且验证者接受。
  • 零知识性意味着拥有 X 是可解的 的证明不会降低找到 X 的解决方案的计算难度
• 要更正式地查看此示例，请参阅 OSL 白皮书。

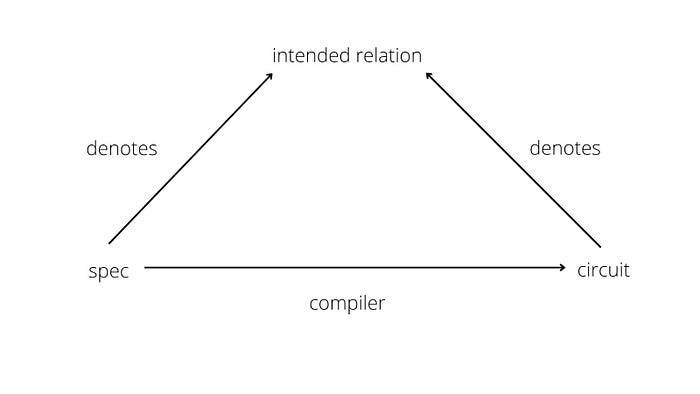
图 1：指称设计

*该图的形式化版本在 Sigma 算术化 论文 （第 47 页的 288）中。这是一个 交换图 。电路编译器的可靠性和完整性都通过该图通勤的陈述来表达，这意味着通过它的同一对象之间的所有路径都是相等的，或者换句话说，编译电路的表示始终等于规范的表示。

如果你知道你的电路表示你想要的关系，并且你知道你的通用证明系统在上述意义上是可靠且完整的，那么你知道你的特定于应用程序的证明系统（即，电路加上通用证明系统）对于该应用程序具有预期的可靠性和完整性属性。

这表明，给定一个经过形式化验证的通用证明系统，以及一个从陈述到电路的经过验证的编译器，人们可以解决证明特定于应用程序的证明系统的正确性的问题，而无需特定于应用程序的正确性证明。

假设

• 一个人可以用机器可读且人类可读的符号编写要由电路表达的陈述，其中编写的陈述具有预期的含义或表示是显而易见的。
• 一个人有一个经过验证的编译器，它将该陈述转换为一个电路，该电路可以证明与源陈述具有相同的表示。
• 电路可以在经过形式化验证的通用概率证明系统上执行。

然后，人们可以生成经过形式化验证的特定于应用程序的概率证明系统，而无需为其他应用程序编写任何额外的证明。这似乎是朝着一种可持续且具有成本效益的 ZK 电路形式化验证方法迈进的有希望的方法。

合成经过形式化验证的程序

弥合我们可以证明的定理和我们可以执行的代码之间的差距通常是一个挑战。例如，我们可能能够证明关于规范的定理，并对该规范进行编码，但随后无法证明该代码实现了规范。或者，我们可能能够证明关于一些代码的定理，但无法将该代码编译为高效的机器代码。或者，我们可以做到这一点，但无法证明机器代码具有与源代码相同的语义。

以下是生态系统支持经过验证的代码高效执行的一些方式的摘要：

• 证明助手 Coq 和 Agda 提供了提取到其他语言以编译为机器代码的功能；就所得机器代码的效率而言，这可能还有不足之处。
• 语言 ATS 提供了证明工具，并声称允许使用 C 和 C++ 的效率进行编程。
• 有各种方法可以将用主流语言（如 C 或 Haskell）编写的代码转译为证明助手，这允许证明关于源程序提取模型的定理。
• 你可以使用 Coq 合成高效的二进制程序（例如，使用 Fiat 或 CertiCoq）
• 证明助手 ACL2 定义了 Common Lisp 的一个子集，具有完整的形式逻辑⁴。当一个定义是可执行的，它可以被编译成高效的代码，并且因为该语言是一个形式逻辑，你可以定义和证明关于代码的定理。
• 有一个验证编译器项目 ATC，从 ACL2 到 C。
• Imandra 定义了 OCaml 的一个子集，具有完整的形式逻辑和一个定理证明器。

形式化方法在现代硬件上的当前局限性

在现代计算的背景下，大多数计算密集型任务都处理向量数学和其他可以在专用硬件（如 GPU、FPGA 和 ASIC）上最有效地完成的令人尴尬的并行问题。

这通常适用于在概率证明系统中构建证明的问题。如果概率证明系统的证明器在专用硬件上实现，则它们将是最有效的，但在实践中，由于在 CPU 上编程更容易以及劳动力市场上更容易获得这些技能，因此它们通常在 CPU 上实现。

对于创建概率证明系统的经过形式化验证的高效执行的实现，正确的做法似乎不是优化 CPU 上的执行速度，而是针对专用硬件，如 FPGA、GPU 或 ASIC。

不幸的是，据我们所知，用于编译经过形式化验证的程序以在 FPGA、GPU 或 ASIC 上运行的工具几乎不存在。

当前进展状态

在硬件验证的背景下，存在数十年关于算术电路形式化验证策略的研究。

• 参见，例如， Drechsler 等人 (2022) 和 Yu 等人 (2016)
• 这项工作具有有限的工业应用，例如，AAMP5（参见 Kern 和 Greenstreet (1997), 第 43 页）
• 这项研究路线并不直接适用于 zk-SNARK 的算术电路的形式化验证，因为硬件中的算术电路和 zk-SNARK 中的算术电路并不完全相同。

存在数十年关于证明概率证明系统的可靠性、完整性和零知识性的研究。

• 这项工作通常是非正式进行的，但为正式证明相同因素的工作提供了一个起点。

例子:

• Groth16
• Bulletproofs
• PLONK

Orbis Labs 正在进行：

• 用于 Σ¹₁ 公式 的 验证Halo 2 电路编译器
• Orbis 规范语言 (OSL)，它提供了一种高级规范语言，我们可以将其编译为 Σ¹₁ 公式
• 一个用于开发经过形式化验证的硬件加速概率证明系统的工具链 (Miya)（仍在基础研究中）：
  • 一种交互组合子算术化理论，用于将经过形式化验证的代码编译为电路
  • 基本概念的定义，如概率证明系统、概率证明系统的可靠性和零知识属性
  • 目标是找到最大限度地精简并适合形式证明的定义

Kestrel Institute 是一个研究实验室，已经使用 ACL2 定理证明器证明了许多 R1CS 小工具的功能正确性。（Kestrel 还做了很多其他的 FV 工作，包括在 Yul、Solidity、以太坊和比特币上。Kestrel Institute 拥有用于从使用 APT 工具包的正式规范中正确构建代码合成的工具，以及使用 Axe 工具包的事后验证，以将二进制文件、字节码和 R1CS 提升到逻辑中，以便根据正式规范进行验证。）

• 他们 形式化并证明了 以太坊 Semaphore R1CS 的部分功能正确性。
• 他们 形式化并证明了 Zcash Sapling 协议的部分功能正确性。该过程的概述：
  • 使用 ACL2 证明助手来形式化 Zcash Sapling 协议的部分规范
  • 在 ACL2 中形式化 rank 1 约束系统 (R1CS)
  • 使用一个提取工具从 Bellman 实现中获取 R1CS 小工具，然后使用 Axe 工具包将 R1CS 提升到逻辑中。
  • 在 ACL2 中证明了这些 R1CS 小工具在语义上等同于它们的规范，这意味着可靠性和完整性。

Aleo 正在开发诸如 Leo 之类的编程语言，这些语言可以编译为诸如 R1CS 之类的约束系统。

• Aleo 旨在创建一个用于 Leo 的验证编译器，使用 ACL2 定理证明器生成和检查正确的编译定理。
• Aleo 还使用 Kestrel Institute 的 Axe 工具包对 R1CS 小工具进行了事后验证。

Nomadic Labs 是一家咨询公司，在 Tezos 上做了很多工作，并且在 Edo 升级时将 Zcash Sapling 协议的受保护交易构建到 Tezos 区块链中。Kestrel Institute 形式化验证了该协议中使用的一些 R1CS。 （Nomadic Labs 也做了很多其他的 FV 工作。）

Andrew Miller 和 Bolton Bailey 正在使用 Lean 定理证明器 在 代数组群模型 中对各种 SNARK 证明系统进行 形式化验证。

Starkware 正在编写 Lean 证明 以检查表示为 Cairo 程序的电路是否符合其规范。

Anoma 团队正在开发 Juvix 语言，作为创建比现有语言更健壮和可靠的，经过形式化验证的智能合约替代方案的第一步。

Veridise 正在进行：

• Medjai，一个用于 Cairo 的符号评估器，旨在用于自动证明搜索
• Picus，一个用于 R1CS 的符号 VM，旨在用于自动证明搜索
• V，一种规范语言，旨在用于表达要通过自动证明搜索证明的陈述
• Coda，一个使用 Coq 证明助手证明 ZK 电路的框架。它使用高级功能性 ZK DSL 来总结电路行为并简化手动证明

Ecne 是一种专用自动证明搜索工具，可以证明 R1CS 约束系统定义了一个函数（全部或部分）。

• 换句话说，它可以证明对于系统可满足的任何输入值，存在系统满足的输出值的唯一组合。
• 这种方法已被证明可用于清除电路中的错误。

来自斯坦福大学的 Alex Ozdemir 正在将有限域求解器添加到 cvc5 SMT 求解器。

来自以太坊基金会的 Lucas Clemente Vella 和 Leonardo Alt 正在研究 有限域上多项式方程的 SMT 求解器。

如何分析每个研究工作/开发项目？

如果你喜欢我们在 “主要问题” 中构建的结构，你可以从以下几个方面分析每个研究工作/开发项目

1. 用于规范的语言；
2. 用于建模约束系统的语言；
3. 他们正在使用的定理证明器；以及
4. 他们正在证明的定理类型，如可靠性、完整性、功能完整性和零知识性。

关于约束系统形式化验证的项目的其他有趣属性是：

• 工具和形式化验证是否是开源的。当用于证明该定理的组件不可用于检查时，很难对定理有信心。
• _可信核心_是什么，即堆栈中哪些软件没有经过形式化验证，以及如果它有错误，可能造成的后果是什么。

未来的研究和开发方向

还有很多工作要做。在安全行业中，对形式化验证的重视程度不够。

基于这篇博文中提出的观察和论点，我们认为以下将是未来研究和开发的一些有趣方向：

1.为形式化验证零知识证明系统奠定基础

• 用于正式证明所需属性的通用证明技术
• 用于证明系统的可重用验证抽象，例如，多项式承诺方案库

2. 改进的规范语言和规范语言之间的验证翻译器。

3. 了解如何创建经过形式化验证的程序以在矢量化硬件（例如，FPGA、GPU 和/或 ASIC）上运行。

4. 我们能否形式化验证旨在自动提高 ZK 电路效率的系统？例如：选择不同电路的系统，以便设置 MPC 更易于并行化，或者允许预先了解部分见证的证明者部分评估电路并使用此信息更快地计算证明的系统。

5. 使用 K 来证明关于 ZK 约束系统的陈述

• 在 K 中定义 Circom/Cairo 的语义
• 使用在 K 中定义的 Rust 语义来证明 arkworks-rs 程序的属性

脚注：

¹我们在文章中没有描述零知识属性，并将撰写另一篇文章来描述它。要描述这一点，你需要深入了解私有输入的概念。（从隐藏明文中正确计算哈希的例子是理解这一点的绝佳例子。）零知识属性是从公共信息中确定私有输入的难度。如果你想使其具有零知识属性，你必须在约束系统中编码私有输入的某个难以反转的函数。零知识属性通常是一种概率度量。然而，如果计算过于简单且输出已知，则可能可以确定地确定输入。

²当存在一个与你想定义的新语言接近的形式定义的 DSL 时，转译器的想法最有意义，然后你可以从你的新语言转译到那个 DSL。然而，那个转译器也应该被形式化验证。

³在我们为具有一些密码组件的系统进行形式化验证的经验中，我们注意到了一些不同的事情：

（1）正式推理“整个”系统的安全属性极其困难。系统设计通常非常复杂，具有许多不同类型的依赖关系。即使是密码组件（从高层次上来说，可能非常小且简单（比如加密、MAC 等）），也可能以非常复杂的方式实现，并支持故障、恢复、备份等。因此，甚至以正式的方式对整个密码组件进行建模也极具挑战性。因此，我们得出的任何正式结论最终都只是针对整个系统的一小部分。我们的方法尚未发展到我们知道如何在形式证明中推理整个系统的程度。

（2）证明助手语言 —— 至少对于密码协议而言 —— 目前具有有限的表达能力。能够直接证明用 C 甚至 Rust 编写的密码协议的定理的工具有限。一般来说，协议开发人员需要处理多个线程和时间问题，而这些很难形式化。例如，Gallina（对于 Coq）没有这样的结构。从这个角度来看，Gallina 对开发人员不太友好，而使用线程的 Rust 则不然。未来正式推理并发软件系统的努力可能会受益于现有抽象的形式化，以便推理此类系统，例如进程演算，例如 π-演算。

⁴Common Lisp 可以被编译成相当高效的代码，非常接近 C 或 Rust。（但是，不如 GPU 高效。此外，并发编程虽然在 Common Lisp 中可用，但不是在其中定义形式逻辑的 ACL2 子集的一部分。）如果你编写了一个可执行的形式规范，那么它通常可以被编译成相当高效的代码，所有这些都发生在定理证明器的语言中。

术语：

如果你使用经过验证或验证的编译器用高级形式语言编写计算的规范并将编译到约束系统，则称为按构造正确。如果你采用现有的约束系统，并尝试证明关于它的属性（最多包括功能正确性），相对于高级形式语言的规范，则称为事后验证。

如果你有兴趣进一步讨论这个话题，或者在这个话题上进行合作，请考虑加入我们的 群聊 或通过 ventali@delendum.xyz 联系我。

• 原文链接： medium.com/delendum/form...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～