沙弗里拉（沙菲）与计算机科学领域的诺贝尔奖

Shafrira (Shafi) 和计算机科学的诺贝尔奖

我采访过一些密码学界的伟人，许多人都提到他们听Shafi Goldwasser演讲的经历，以及她如何激励了他们的职业生涯。2012年，她获得了图灵奖（计算机科学的诺贝尔奖）[here]：

在她发明的众多事物中，包括概率加密的共同发明 [ here][1]:

以及零知识证明的共同发明 [2]:

她目前是麻省理工学院的 RSA 电气工程和计算机科学教授 [ here]。在其职业生涯中，Shafi 获得了许多奖项，包括 2012 年的图灵奖，以及 2019 年牛津大学授予的荣誉科学博士学位。Shafi 于 1979 年获得学位（卡内基梅隆大学），然后在 1984 年获得博士学位（来自加利福尼亚大学）[ here]：

在 2010 年至 2020 年期间，她还被评为全球第 12 位最具影响力的计算机科学研究员。

Blum-Goldwasser 概率加密

Shafi 的博士生导师是强大的 Manuel Blum， 他们共同创建了概率加密。通过公钥加密，Alice 可以将两条可能的消息（“0”或“1”）发送给 Bob。如果 Eve 知道可能的消息（“0”或“1”），她将使用 Bob 的公钥对每个消息进行加密，然后将结果与 Alice 发送的密文消息进行匹配。因此，Eve 可以确定 Alice 发送给 Bob 的内容。为了克服这个问题，Blum-Goldwasser 方法是一种使用概率公钥加密方案的公钥算法 [ here]：

该加密方法使用 Blum-Blum-Shub (BBS) 技术来生成密钥流 [ here]。最初，我们创建两个素数（p 和 q），然后计算 N：

N = p.q

公钥是 N，私钥是 p 和 q，其中 p 和 q：

p (mod 4) = 3

q (mod 4) = 3

例如，我们可以选择 p= 239，q= 179，因为当我们进行 (mod 4) 运算时，两者都会给我们 3：

>>> p=239
>>> q=179
>>> p%4
3
>>> q%4
3

维基百科定义的基本方法是：

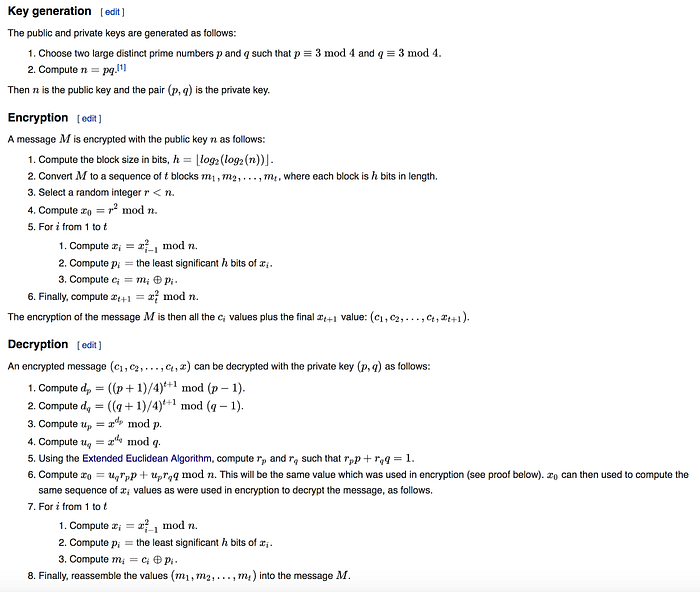
代码如下 [ here]：

iimport numpy as np
import binascii
import Crypto.Util.number
from Crypto import Random
import sys
import random

def xgcd(a, b):
    """return (g, x, y) such that a*x + b*y = g = gcd(a, b)"""
    x0, x1, y0, y1 = 0, 1, 1, 0
    while a != 0:
        (q, a), b = divmod(b, a), a
        y0, y1 = y1, y0 - q * y1
        x0, x1 = x1, x0 - q * x1
    return b, x0, y0

## Method from https://stackoverflow.com/questions/7396849/convert-binary-to-ascii-and-vice-versa
# 来自 https://stackoverflow.com/questions/7396849/convert-binary-to-ascii-and-vice-versa 的方法
def to_bits(text, encoding='utf-8', errors='surrogatepass'):
    bits = bin(int(binascii.hexlify(text.encode(encoding, errors)), 16))[2:]
    return bits.zfill(8 * ((len(bits) + 7) // 8))
def from_bits(bits, encoding='utf-8', errors='surrogatepass'):
    n = int(bits, 2)
    return int2bytes(n).decode(encoding, errors)
def int2bytes(i):
    hex_string = '%x' % i
    n = len(hex_string)
    return binascii.unhexlify(hex_string.zfill(n + (n & 1)))
## Derived from https://github.com/coenvalk/blum-goldwasser-probabilistic-encryption/blob/master/blumgoldwasser.py
# 来源于 https://github.com/coenvalk/blum-goldwasser-probabilistic-encryption/blob/master/blumgoldwasser.py
def BGW_enc(p, q, x, m):
    n = p * q

    # assert p%4 == 3 and q%4 == 4
    # 断言 p%4 == 3 且 q%4 == 4
    k = int(np.log2(n))
    h = int(np.log2(k))
    t = len(m) // h
    xi = x
    c = ''
    for i in range(t):
        mi = m[i*h:(i + 1)*h]
        xi = (xi ** 2) % n
        xi_bin = bin(xi)
        pi = xi_bin[-h:]
        mi_int = int(mi, 2)
        pi_int = int(pi, 2)
        ci = pi_int ^ mi_int
        ci_bin = format(ci, '0' + str(h) + 'b')
        c += ci_bin
    xt = (xi ** 2) % n
    return c, xt

def BGW_dec(p, q, a, b, xt, c):
    assert a*p + b*q == 1
    n=p*q
    k = int(np.log2(n))
    h = int(np.log2(k))
    t = len(c) // h
    d1 = pow((p + 1) // 4,(t + 1) , (p - 1))
    d2 = pow((q + 1) // 4,(t + 1) , (q - 1))
  #  d2 = (((q + 1) // 4)**(t + 1)) % (q - 1)
    u = pow(xt,d1,p)
    v = pow(xt,d2, q)
    x0 = (v*a*p + u*b*q) % n
    xi = x0
    m = ''
    for i in range(t):
        ci = c[i*h:(i + 1)*h]
        xi = (xi**2) % n
        xi_bin = bin(xi)
        pi = xi_bin[-h:]
        ci_int = int(ci, 2)
        pi_int = int(pi, 2)
        mi = pi_int ^ ci_int
        mi_bin = format(mi, '0' + str(h) + 'b')
        m += mi_bin
    return m
p = 499
q = 547
bits=10
msg='Hello'
if (len(sys.argv)>1):
        bits=int(sys.argv[1])
if (len(sys.argv)>2):
        msg=(sys.argv[2])
while True:
 p=Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
 if (p%4==3): break

while True:
 q=Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
 if (q%4==3): break
m=to_bits(msg)

a=1
b=1
_,a,b=xgcd(p,q)

r= random.getrandbits(bits)
x0 = (a*p*r + b*q+r) % (p*q)

c, xt = BGW_enc(p, q, x0, m)
print(("Message: %s" % msg))
print(("   %s" % m))
print(("\nNo of bits in prime is %d" % bits))
print(("p= %d" % p))
print(("q= %d" % q))
print(("a= %d" % a))
print(("b= %d" % b))
print(("r= %d" % r))
print(("x0= %d" % x0))
print(("ap+bq: %d" % (a*p+b*q)))
print("\nCiphertext:", c)
d = BGW_dec(p, q, a, b, xt, c)

print(("Decrypted: %s" % from_bits(d)))

一个示例运行 [ here]：

Message: Hello
   0100100001100101011011000110110001101111No of bits in prime is 16
p= 44119
q= 50647
a= 24633
b= -21458
r= 14161
x0= 2119402684
ap+bq: 1Ciphertext: 0001011100111001001110010010011100101011
Decrypted: Hello

Goldwasser–Micali (GM) 密码系统

通过公钥加密，Alice 可以将两条可能的消息（“0”或“1”）发送给 Bob。如果 Eve 知道可能的消息（“0”或“1”），她将使用 Bob 的公钥对每个消息进行加密，然后将结果与 Alice 发送的密文消息进行匹配。因此，Eve 可以确定 Alice 发送给 Bob 的内容。为了克服这个问题，Goldwasser–Micali (GM) 方法实现了一种概率公钥加密方案。它还支持同态加密的使用，由 Shafi Goldwasser 和 Silvio Micali 于 1982 年开发。

该方法的演示 here。

在概率加密方法中，Alice 选择明文 (m) 和随机字符串 (r)。接下来，她使用 Bob 的公钥加密消息对 (m,r)。如果该值是随机的，那么 Eve 将无法获得已使用的消息和随机值的范围。

如果 Bob 想要创建他的公钥和私钥。他首先为他的私钥选择两个随机素数，然后计算 N：

N=p.q

p 和 q 的值将是他的私钥，N 将构成他的公钥的一部分。对于他公钥的第二部分，他确定：

a=pseudosquare(p,q)

我们选择一个 a 的值，这样就没有解决方案了：

u² ≡ a (mod N)

这被定义为没有二次剩余（here）。

Bob 的公钥是 (N,a)，私钥是 (p,q)。

密钥生成

密钥加密方法变为：

Bob 选择 p 和 q。

Bob 选择一个 (a/p) = (a/q) = -1 的 a。这是一个 Jacobi 符号计算。

Bob 发布 N 和 a。

加密

为了给 Bob 加密。Alice 选择 m，它是一个要加密的位 m∈0,1。

然后 Alice 使用 Bob 的 (N,a) 值来计算：

c=r² (mod N) 如果 m=0

c=a r² (mod N) 如果 m=1

Alice 随机选择 r，因此 Eve 将无法发现消息，因为当 m=0 时，随机值将包含所有可能的模 N 平方。

Alice 将密文位 (c) 发送给 Bob。

解密

然后 Bob 计算 Jacobi 符号 (c/p) 并得到：

m=0 如果 c/p=1

m=1 如果 c/p=−1

该方法的演示 here。代码的轮廓来自 here：

## https://asecuritysite.com/encryption/goldwasser
## 基于 https://gist.github.com/brunoro/5893701/
from unicodedata import normalize
from string import ascii_letters
from random import randint
import sys
from functools import reduce

## Miller-Rabin probabilistic primality test (HAC 4.24)
# Miller-Rabin 概率素性测试 (HAC 4.24)
## returns True if n is a prime number
# 如果 n 是素数，则返回 True
## n is the number to be tested
# n 是要测试的数字
## t is the security parameter
# t 是安全参数

def miller_rabin(n, t):
    assert(n % 2 == 1)
    assert(n > 4)
    assert(t >= 1)
    # select n - 1 = 2**s * r
    # 选择 n - 1 = 2**s * r
    r, s = n - 1, 0
    while r % 2 == 0:
        s += 1
        r >>= 1 #r = (n - 1) / 2 ** s
    for i in range(t):
        a = randint(2, n - 2) # this requires n > 4
        # 这需要 n > 4
        y = pow(a, r, n) # python has built-in modular exponentiation
        # python 具有内置的模幂运算
        if y != 1 and y != n - 1:
            j = 1
            while j <= s - 1 and y != n - 1:
                y = pow(y, 2, n)
                if y == 1:
                    return False
                j += 1
            if y != n - 1:
                return False
    return True
def is_prime(n):
    if n in [2, 3]:
        return True
    if n % 2 == 0:
        return False
    return miller_rabin(n, 10)
def nearest_prime(n):
    if is_prime(n):
        return n
    if n % 2 == 0:
        n += 1
    i = 0
    while True:
        i += 1
        n += 2
        if is_prime(n):
            return n
def big_prime(size):
    n = randint(1, 9)
    for s in range(size):
        n += randint(0, 9) * s**10
    return nearest_prime(n)
def is_even(x):
    return x % 2 == 0
## calculates jacobi symbol (a n)
# 计算雅可比符号 (a n)
def jacobi(a, n):
    if a == 0:
        return 0
    if a == 1:
        return 1
    e = 0
    a1 = a
    while is_even(a1):
        e += 1
        a1 =a1// 2
    assert 2**e * a1 == a
    s = 0
    if is_even(e):
        s = 1
    elif n % 8 in {1, 7}:
        s = 1
    elif n % 8 in {3, 5}:
        s = -1
    if n % 4 == 3 and a1 % 4 == 3:
        s *= -1
    n1 = n % a1

    if a1 == 1:
        return s
    else:
        return s * jacobi(n1, a1)
def quadratic_non_residue(p):
    a = 0
    while jacobi(a, p) != -1:
        a = randint(1, p)
    return a
def xeuclid(a, b):
    """ return gcd(a,b), x and y in 'gcd(a,b) = ax + by'.
    """
    x = [1, 0]
    y = [0, 1]
    sign = 1

    while b:
        q, r = divmod(a, b)
        a, b = b, r
        x[1], x[0] = q*x[1] + x[0], x[1]
        y[1], y[0] = q*y[1] + y[0], y[1]
        sign = -sign

    x = sign * x[0]
    y = -sign * y[0]
    return a, x, y

def gauss_crt(a, m):
    """ return x in ' x = a mod m'.
    """
    modulus = reduce(lambda a,b: a*b, m)

    multipliers = []
    for m_i in m:
        M = modulus // m_i
        gcd, inverse, y = xeuclid(M, m_i)
        multipliers.append(inverse * M % modulus)

    result = 0
    for multi, a_i in zip(multipliers, a):
        result = (result + multi * a_i) % modulus
    return result
def pseudosquare(p, q):
    a = quadratic_non_residue(p)
    b = quadratic_non_residue(q)
    return gauss_crt([a, b], [p, q])
def generate_key(prime_size = 6):
    p = big_prime(prime_size)
    q = big_prime(prime_size)
    while p == q:
        p2 = big_prime(prime_size)
    y = pseudosquare(p, q)
    n=p*q

    keys = {'pub': (n, y), 'priv': (p, q)}
    return keys
def int_to_bool_list(n):
    return [b == "1" for b in "{0:b}".format(n)]
def bool_list_to_int(n):
    s = ''.join(['1' if b else '0' for b in n])
    return int(s, 2)
def encrypt(m, pub_key):
    bin_m = int_to_bool_list(m)
    n, y = pub_key
    def encrypt_bit(bit):
        x = randint(0, n)
        if bit:
            return (y * pow(x, 2, n)) % n
        return pow(x, 2, n)
    return list(map(encrypt_bit, bin_m))
def decrypt(c, priv_key):
    p, q = priv_key
    def decrypt_bit(bit):
        e = jacobi(bit, p)
        if e == 1:
            return False
        return True
    m = list(map(decrypt_bit, c))
    return bool_list_to_int(m)
def normalize_str(s):
    u = str(s)
    valid_chars = ascii_letters + ' '
    un = ''.join(x for x in normalize('NFKD', u) if x in valid_chars).upper()
    return un.encode('ascii', 'ignore')
def int_encode_char(c):
    ind = c
    val = 27 # default value is space
    # 默认值是空格
    # A-Z: A=01, B=02 ... Z=26
    if ord('A') <= ind <= ord('Z'):
        val = ind - ord('A') + 1
    return "%02d" % val
def int_encode_str(s):
    return int(''.join(int_encode_char(c) for c in normalize_str(s)))
message='hello'
key = generate_key()
print(key)
m = int_encode_str(message)
print("\nMessage:",message, "Encoded:",m)
print("\n消息:",message, "编码:",m)
enc = encrypt(m, key['pub'])
print("\nEncrypted:",enc)
print("\n已加密:",enc)
dec = decrypt(enc, key['priv'])
print("\nDecrypted:",dec)
print("\n解密:",dec)

使用消息“hello”的示例运行给出了：

{'pub': (810571289346697L, 417803374284193L), 'priv': (16117253, 50292149)}Message: hello Encoded: 805121215Encrypted: [102605923461178L, 143126886286230L, 745770432842022L, 168824391145739L, 261618935651655L, 460849071043598L, 798955941491864L, 487047472970991L, 397987844446930L, 743669716499309L, 669942878308283L, 178548007880797L, 645225183019810L, 779540939053212L, 384395411075108L, 782842239347547L, 691841667554224L, 181138769678461L, 779305447143669L, 451333672269645L, 32858488530236L, 678286539525029L, 51434079116117L, 281928894615544L, 156989394653382L, 31002122426343L, 334583216645061L, 216935340466474L, 38608665591955L, 332742987467921L]Decrypted: 805121215

结论

Goldwasser–Micali (GM) 密码系统是一种公钥方法，已经存在一段时间（1982 年），并且是第一个概述概率方法用于加密的方法。按照今天的标准，它效率不高，但它的方法现在正被用于同态加密的实现中，例如使用[paper]。对于 Safi 来说，她仍然与人共同领导麻省理工学院的密码学和信息安全 (CIS)，其中包含密码学历史上一些最杰出的人：

这是一个最近的演讲：

参考文献

[1] Goldwasser, S., & Micali, S. (1982, May). Probabilistic encryption & how to play mental poker keeping secret all partial information. In Proceedings of the fourteenth annual ACM symposium on Theory of computing (pp. 365–377).

[2] Goldwasser, S., Micali, S., & Rackoff, C. (2019). The knowledge complexity of interactive proof-systems. In Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali (pp. 203–225).

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～