Solidity ABI 编码的深度解析：第一部分

本文是Solidity ABI编码的深入解析教程的第一部分，主要介绍了ABI编码的基础知识、先决条件，以及静态类型和动态类型的编码规则。通过具体的例子，详细解释了如何将函数参数编码成EVM可以理解的字节序列，包括函数选择器、Head-Tail结构、偏移量的计算等关键概念，旨在帮助开发者掌握Solidity ABI编码的核心原理。

Solidity ABI 编码的深度心智模型：第一部分

Solidity ABI 编码的深度心智模型：第一部分

对于 Solidity 开发者来说，ABI 编码/解码是必须掌握的主题。

这是将你与其他人区分开来的主题之一 —— 让你成为一个 10 倍的 solidity 开发者。

另一方面，这是一个可能很难掌握的主题。它是 Solidity 官方文档中最复杂的部分之一。 （相信我，我尝试过“解读”它。）本系列文章的目标是简化每个 Solidity 开发者的 ABI 编码。

阅读第 0 部分，了解为什么要在 Solidity 中学习 ABI 编码/解码 👇

为什么要学习 Solidity 的难点 [ ABI 编码系列：第 0 部分 ]

Solidity ABI 编码介绍及其对 solidity 开发者重要性

现在，让我们开始吧。

快速回顾

EVM 中的 应用程序二进制接口 (ABI) 定义了如何编码和解码数据结构和函数调用，以便在合约和外部参与者（如 web3 客户端或链下代码）之间进行通信。

它充当高级 Solidity 代码和低级 EVM 操作之间的翻译层。

ABI 编码在所有 EVM 兼容链上都是严格定义、确定性和一致的，这使得以太坊工具（如 ethers.js、web3.js、Foundry 和 Remix）能够以可预测的方式与智能合约交互，而根本无需理解你的 Solidity 源代码。

如果你曾经调用过这样的函数：

myContract.call(abi.encodeWithSignature("transfer(address,uint256)", recipient, amount));

或者像这样解码事件数据：

abi.decode(data, (uint256, address));

你已经接触过 ABI 编码了。

你已经看到了对函数调用进行编码后产生的十六进制 blob，如下所示：

0xa9059cbb0000000000000000000000005B38Da6a701c568545dCfcB03FcB875f56beddC40000000000000000000000000000000000000000000000000000000000000064

这是一个 ABI 编码的函数调用，也是 EVM 在执行你的代码时所理解的内容。本文正是关于我们如何获得这个编码的十六进制值的。

我编写此 ABI 编码系列文章的目标是：

  • 提供掌握 ABI 编码的先决条件
  • 深入解释 ABI 编码的实际工作原理
  • 提供 可靠的心智模型 来编码任何给定的函数和参数

我将带你了解 ABI 编码数据的精确结构，并帮助你掌握 编码的基本定律，这些定律控制着任何输入（无论其复杂性如何）如何转换为 EVM 可以执行的原始字节。

在本指南结束时，你将能够查看任何函数签名和参数，并逐字节手动重建精确的 ABI 编码的调用数据 — 并且可以通过解码来做到相反。

但首先，你必须理解一些先决条件。

新手入门

a. MSB 和 LSB

  • MSB：最高有效字节 (MSB) 是对总值贡献 最大 的字节
  • LSB：最低有效字节 (LSB) 是对总值贡献 最小 的字节

例如，考虑十进制数 2,984:

  • 将数字 4 更改为 5 会使数字增加 1，但是
  • 将数字 2 更改为 3 会使数字增加 1,000。

这个概念也适用于字节和位。

让我们以整数 0x12345678 （十进制为 305419896）为例，它占用 4 个字节（32 位）：

字节位置 大端序 小端序
字节 0 0x12（最高有效位） 0x78（最低有效位）
字节 1 0x34 0x56
字节 2 0x56 0x34
字节 3 0x78（最低有效位） 0x12（最高有效位）

b. 端序：大端序与小端序

端序 是指多字节值在内存中的布局方式：

  • 大端序 意味着 最高有效字节在前
  • 小端序 意味着 最低有效字节在前

例如，假设一个 uint32 的十进制值为 305419896。在十六进制中，它是 0x12345678

现在，大端序编码 将像这样存储它：

内存布局（大端序）：[12][34][56][78]

因此，MSB 0x12 在最前面。

另一方面，小端序编码 将像这样存储它：

内存布局（小端序）：[78][56][34][12]

这里，LSB 0x78 在最前面 — 一切都被颠倒了。

✍️

Solidity ABI 编码 *始终使用大端序*，因为它已针对以太坊虚拟机 (EVM) 通信进行了标准化。

c. 填充

在 ABI 编码中，填充是指添加额外的零字节，以使值与 32 字节（256 位）边界对齐。

在 Solidity ABI 中，大多数值都编码为 32 字节（256 位）。

如果你的数据较小（如 1 字节的布尔值或 20 字节的地址），则必须对其进行填充（通常用零）才能变为 32 字节。

你将会注意到 2 种类型的填充：

  • 左填充

    用于整数或地址。（对于静态类型）：

    • 你将实际值放在 32 字节字的 右端
    • 所有剩余的 左侧未使用的字节 都用 0x00 填充
    • 例如，如果我们对数字 1 进行编码 - uint256(1)
0x0000000000000000000000000000000000000000000000000000000000000001

  • 右填充

    用于

    bytes<M>（例如 bytes3）和字符串/字节

    (

    用于

    动态类型)

    • 你将实际值放在块的 左端
    • 所有剩余的 右侧未使用的字节 都用 0x00 填充
    • 例如，bytes("abc")
// "abc" in hex - 616263
0x6162630000000000000000000000000000000000000000000000000000000000

这是 右填充的，并且 数据在 32 字节块中左对齐。

d. 静态类型与动态类型

这使我们能够区分 Solidity 中的类型 ( 这比你想象的更有用)

Solidity 中有两种主要类型：

  1. 静态类型： 一种大小在 编译时固定 的类型。
  2. 动态类型： 一种大小可能在 运行时变化 的类型。

以下是一个快速表格，其中列出了属于每个类别的不同类型：

类别 示例
静态 uint256、bool、address、bytes32、uint[2]、固定大小的元组
动态 string、bytes、uint[]、address[]、动态元组

确定类型非常重要，因为 ABI 编码机制以及填充会根据你要编码的类型而有所不同。

e. Calldata

在 Solidity 中，calldata 是传递给函数调用的只读、不可修改的输入数据。它包括从外部源（钱包、脚本或合约）发送到函数以调用它的所有内容。

从 ABI 编码的角度来看，calldata 是存储完整 ABI 编码的有效负载 的位置。

此有效负载包括：

  1. 一个 4 字节的函数选择器
  2. ABI 编码的参数，根据 ABI 规则进行填充和布局（我们将在下一节中学习的规则）

每次从外部调用合约函数时（无论是从 Remix、Ethers.js 还是 Foundry），都会使用 ABI 编码规则构造 calldata，并将其发送到 EVM 以执行。

这是一个简化的结构：

calldata = [函数选择器][参数编码]

💡

了解如何在 calldata 中对参数进行编码是 ABI 编码的全部目的。解码 calldata 后，你可以重建调用了哪个函数以及传递了哪些值。

f. 函数选择器

函数选择器 是 calldata 的前 4 个字节。它唯一地标识应在合约上调用的函数。

快速浏览一下它的工作原理：

  • Solidity 通过获取函数签名的 Keccak-256 哈希的前 4 个字节来计算 函数选择器。
  • 函数签名 是一个字符串，由函数名称及其参数的精确类型组成，不带空格。

例如：

function transfer(address to, uint256 amount)

它的签名字符串是：

"transfer(address,uint256)"

// 它的 keccak256() 哈希值为：0xa9059cbb2ab09eb219583f4a59a5d0623ade346d962bcd4e46b11da047c9049b

前 4 个字节 (a9059cbb) 是 函数选择器，它成为 calldata 的前缀。

每个 ABI 编码的 calldata 都必须以正确的函数选择器开头，以便 EVM 知道要将哪个函数分派到合约中。

现在你已经具备了理解 ABI 编码内部工作原理所需的基础知识和先决条件。

让我们从编码定律开始。

ABI 编码的基本规则

对于任何给定的函数和参数：

  1. 以 头尾 形式创建一个包含所有函数参数的元组（先是所有头，然后是所有尾）
  2. 编码所有 HEAD
  3. 编码所有 TAIL
  4. 组合所有编码以获得最终编码值

这些是基本定律，并且永远不会改变。

如果你不知道这一切意味着什么，请不要担心。 允许我定义它们，然后用示例解释。 请耐心等待。

现在，让我们首先定义这些术语：

  1. 编码
    1. 编码是指将高级值（如数字、字符串或数组）转换为 EVM 可以理解和使用的固定字节序列。
    2. 在 Solidity ABI 编码中：
      1. 所有数据都以 32 字节（256 位）块 进行编码。
      2. 每个值都根据其类型以可预测的方式进行转换
      3. 目标是创建一个可以解码回链上原始值的二进制表示形式

你可以将编码视为从人类可读的值转换为 EVM 可读的二进制文件。

  1. 什么是 HEAD
    1. 每当我们编码一个给定的值（或一组值）时，最终编码结果中有两个部分：head 和 tail。
    2. head 是每个参数的编码值的第一部分。
    3. 它要么包含实际值（对于固定大小的类型），要么指向可以找到该值的位置（对于动态类型）。
    4. Head 编码规则：
      1. head 的编码取决于要编码的类型：

    • 对于静态类型：

    • head 包含实际的 编码值，填充为 32 字节。

    • 这些值完全 存在于 head 中 —— 静态类型没有 tail。

    • 对于动态类型：

    • head 不包含实际值。

    • 相反，它包含一个 32 字节的偏移量，该偏移量告诉 EVM 在哪里可以找到 tail —— 即实际数据。
  1. 什么是 TAIL
    1. tail 是编码值的第二部分，其中包含 动态类型 的实际数据。
    2. 它位于 head 部分之后，大小可能会因参数值而异。
    3. Tail 编码规则：
      1. 对于静态类型，tail 始终为空 - 没有 TAIL。
      2. 对于动态类型，它包括实际数据。动态类型数据的 tail 包括 2 个主要内容：
  • 一个 长度前缀（字符串或数组有多长）
  • 实际字节，填充后使所有内容与 32 字节块对齐。

这些是在 EVM 中编码任何给定值集的最基本规则集。它们将始终为真。

✍️

*注意：* 在一些复杂的例子中，我们可能会看到一些额外的注意事项。

例如： a. 动态类型的编码需要理解 *偏移量。（* 我们稍后会介绍）

b. 动态嵌套数组或结构体内部数组的编码等将具有新的 \相对偏移量*** 术语。 我们将在后续部分中介绍此类示例。

但同样，基本原理将始终成立。

直观地理解 HEAD-TAIL

为了直观地理解 HEAD-TAIL 的概念，让我们举两个非常简单的例子：

带有 2 个静态类型参数的函数 staticType

function staticType(uint256 a, uint256 b) public pure returns (bytes memory){
        return msg.data;
}

带有 1 个动态类型参数的函数 dynamicType

function dynamicType(string memory s) public pure returns(bytes memory ){
        return msg.data;
    }

当你执行这些函数时，它们将返回 calldata，calldata 是函数选择器以及传递的参数 的ABI 编码值。

让我们快速看一下它们的每个编码的 calldata：

staticType 函数的 Calldata：

函数选择器：74b4a150
 ------------
 [000]: 0000000000000000000000000000000000000000000000000000000000000001
 [020]: 0000000000000000000000000000000000000000000000000000000000000002

其可视化表示形式可以看作是：

img

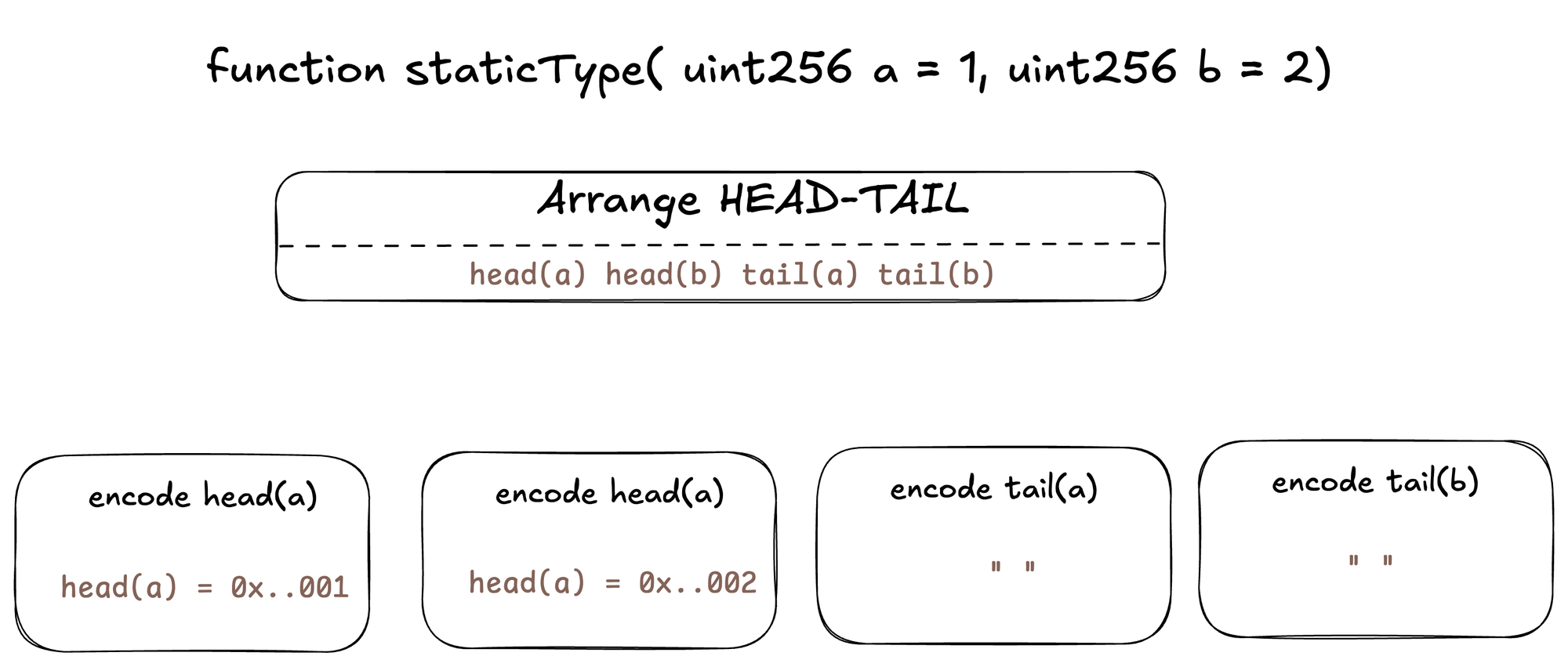
  • 请注意，静态类型的编码就像 head 本身包含编码值一样简单
  • 而静态类型的 tail 为空。

dynamicType 函数的 Calldata：

 函数选择器：46641647
 ------------
 [000]: 0000000000000000000000000000000000000000000000000000000000000020
 [020]: 000000000000000000000000000000000000000000000000000000000000000c
 [040]: 4465636970686572436c75620000000000000000000000000000000000000000

其可视化表示形式可以看作是：

img

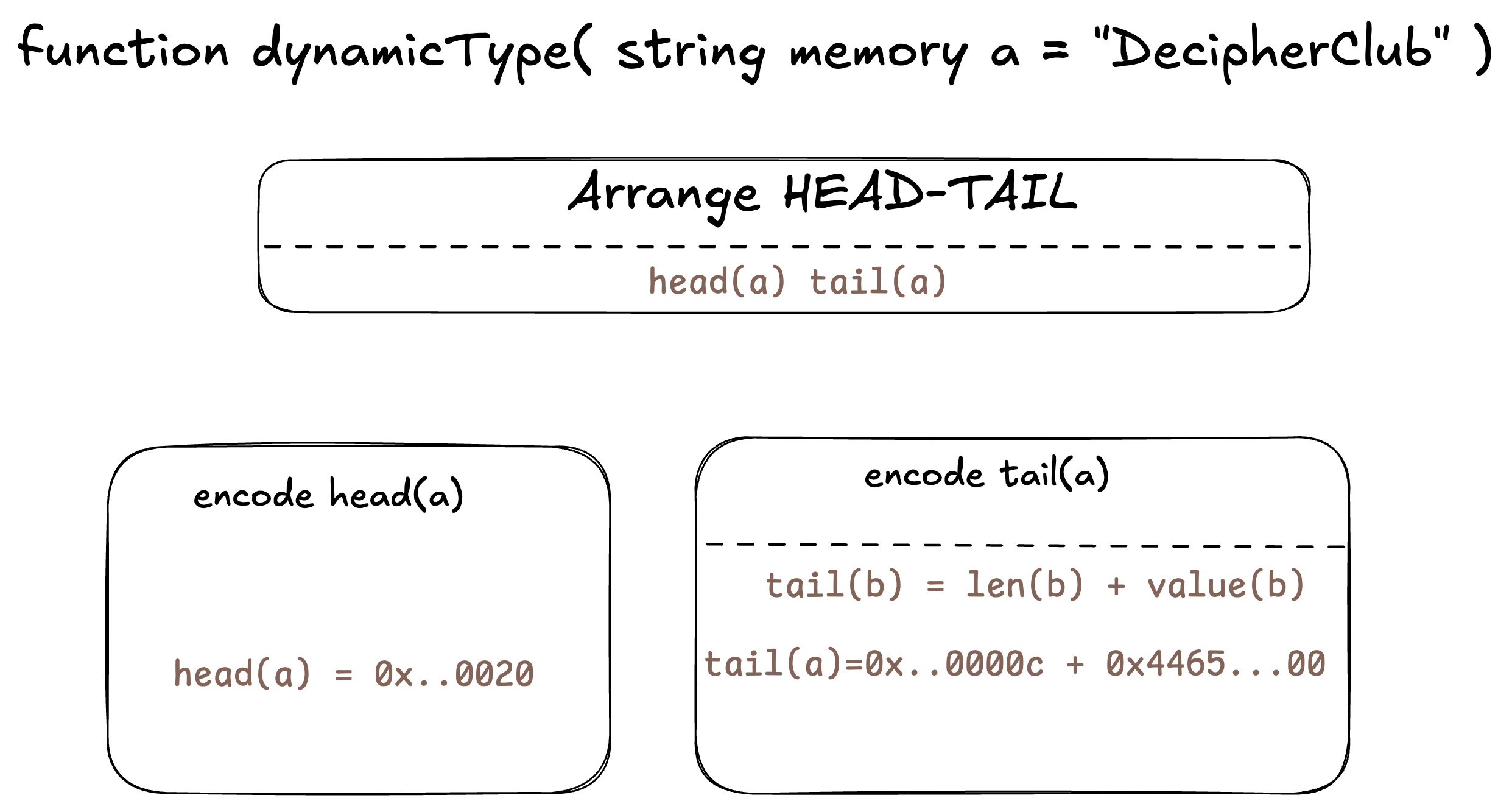
  • head 包括 0x20，它是指向 tail(a) 所在位置的指针。（在上方的 calldata 输出中查看）
  • 而 tail 包括实际值，即（字符串的长度 + 编码值）

注意： 这仅是为了显示 head-tail 的排列方式。我们将在下一个详细示例中探讨编码机制

现在，我们的下一个任务是应用这些规则并查看它们是否有效。

专家提示： 你用下面解释的例子迭代得越多，你就越能理解 ABI 编码的工作原理。

应用规则

你现在已经对理解 ABI 编码的工作原理所需的所有概念有了理论上的理解。

你还拥有一套永远不会改变的规则。

我们现在需要做的就是应用这些规则并验证它们是否按预期工作。

我们将把编码规则应用于 3 种不同类型的函数：

  • 仅带有静态类型参数的函数
  • 仅带有动态类型参数的函数
  • 混合类型的函数（静态 + 动态）

首先，我们将完全专注于静态类型，主要理解以下内容：

  • 以元组形式排列函数参数是什么样的？
  • 以 heads 和 tails 形式排列又是什么样的？
  • 编码是什么样的？

现在，甚至不用担心动态类型。

🧠

这不仅仅是为了获得正确的答案。 而是为了建立肌肉记忆，了解如何分析任何函数并每次都使用相同的心智模型来获得正确的 calldata。

仅具有静态类型的函数

让我们从一个只有静态类型参数的简单例子开始：

    // 参数 ( a=1, b=2, c=3 ) 
    function encodeFirst(uint256 a, uint256 b, uint256 c) public pure returns (bytes memory) {
        return msg.data;
    }

第 1 步：以元组思考

回顾第一条规则，将所有函数参数分组到一个具有头尾形式的元组中。

请记住，solidity 始终将所有参数视为它们是一个组合的元组。

因此我们像这样思考输入：

这个元组有 3 个元素：a、b 和 c。

tuple(a, b, c)
// 以头尾形式形成它

encoded = [head(a)] [head(b)] [head(c)] [tail(a)] [tail(b)] [tail(c)]

第 2 步：可视化头尾布局

现在，回顾一下 静态类型 值的头和尾的通用规则：

由于所有类型都是静态的：

  • 每个 head(x) = x 的编码值（填充为 32 字节）
  • 每个 tail(x) = 空（因为静态类型没有尾）
encoded = [head(a)] [head(b)] [head(c)] [tail(a)] [tail(b)] [tail(c)]

所以它看起来像这样：

[ head(a) ] → a 的 32 字节
[ head(b) ] → b 的 32 字节
[ head(c) ] → c 的 32 字节
[ tail(a) ] →（空）
[ tail(b) ] →（空）
[ tail(c) ] →（空）

即使尾部为空，我们仍然在精神上放置它们以加强结构 — 这将使我们以后能够无缝地处理动态情况。

第 4 步：确定参数类型并编码每个值

我们有 3 个参数，并且都是静态类型 (uint256)。

现在让我们编码参数。在我们的例子中，参数是：（a=1, b=2, c=3）

为了编码，回顾一下静态类型的编码规则：

  • 所有参数始终编码为 32 字节
  • 静态类型的 head 编码是参数本身的编码值。
  • 编码遵循 大端布局（最高有效字节在前），并在 左侧 用零填充（即右对齐。
 head(a): 0000000000000000000000000000000000000000000000000000000000000001
 head(b): 0000000000000000000000000000000000000000000000000000000000000002
 head(c): 0000000000000000000000000000000000000000000000000000000000000003
 tail(a): "" // 空
 tail(b): "" // 空
 tail(c): "" // 空

第 5 步：组合 HEAD 和 TAIL

我们现在已经编码了此函数中所有参数的头和尾。

如果我们将它们全部组合在一起，我们应该得到发送到合约的所有参数的编码值。

应该预先考虑函数选择器：

我们不能忘记函数选择器。

对 Solidity 中函数的每次调用都以一个 4 字节的函数选择器 开始。

要计算函数选择器，你可以使用来自 foundry 的 cast CLI 工具并运行此命令：

cast sig "encodeFirst(uint256,uint256,uint256)"

// 这基本上是 keccak256("encodeFirst(uint256,uint256,uint256)")[:4]
// 即函数签名的 keccak256 哈希的前 4 个字节

这将返回 0xb2bc9513 作为 encodeFirst() 函数的函数选择器。

现在将选择器添加到编码参数：

final calldata =
  0xb2bc9513 // 函数选择器
  0000000000000000000000000000000000000000000000000000000000000001
  0000000000000000000000000000000000000000000000000000000000000002
  0000000000000000000000000000000000000000000000000000000000000003

编码 仅静态类型 的值非常容易。

真正的挑战始于动态类型。让我们采用一个简单的 字符串( 一个动态类型 *)** 并应用我们的规则，看看我们是否可以正确编码。

另一个有用的 cast CLI 命令是：cast pretty-calldata <calldata> 这提供了 calldata 的可读的漂亮版本。

但首先，偏移量......

再次回顾这些规则。

对于动态类型：

  • head 包含一个 32 字节的偏移量，该偏移量指向 tail —— 即实际值。

对于静态值，我们只是简单地编码了值本身并将其放在 head 部分中。（而 tail 为空。）

动态值有所不同。head 必须包含指向 tail 所在位置的偏移量/位置。

但是，我们如何计算给定动态值或一组动态值作为函数参数的偏移量？

动态类型值的偏移量计算规则

当参数是动态的时，其 head 必须 指向其尾开始的位置，并且此值必须 编码为 uint256。

该偏移量是从整个参数编码块的开始处开始测量的（即，紧接在 4 字节函数选择器之后），而不是从 calldata 的开始处开始测量的。

对于位置 i 处的动态参数：

  • head 包含指向其尾开始的偏移量，该偏移量等于：
  • 32 * 参数数量 + 位置 i 处参数之前 tail 的总大小

换句话说：

  1. 计数 head 部分 的大小（始终为 32 × 参数数量）
  2. 加起来 所有先前尾部的总大小（仅限此动态参数之前的尾部）
  3. 结果是 此参数尾部的偏移量，这就是 head 中的内容

示例分解

对于这样的函数：

function f(string a, string b)

or

encoded = [head(a)][head(b)][tail(a)][tail(b)]

  • head(a) = 0x40：

    • head(a) 表示字符串 a 的 head，它是第一个参数。（此参数之前没有 tail。所以）*
    • 所以，我们只关心参数的总值，即 2。（参数 a 和 b）
    • 按照规则：32 2 得到 64，也就是 0x40（因为第一个 tail 在两个 32 字节的 head 之后开始，它们一起占据 64 字节。）*
    • 因此，head(a) 为 0x40，表示可以从位置 0x40 找到 tail（字符串 a 的实际值）。

  • head(b) = 0x80

    • head(b) 表示字符串 b 的 head，它是第二个参数。

    • 前 2 个参数（a 和 b）都是动态类型，因此它们的 head 占据了前 32 * 2 = 64 字节 → 这是十六进制的 0x40。（所以 tail(a) 从偏移量 0x40 开始，我们已经知道了）

    • 现在，对于参数 b，我们必须首先考虑以下事项：

    • 两个参数 a 和 b 的 head 占据了 64 个字节。

    • 需要以下空间：

         tail(a)

      即：

      • a 是一种字符串类型，这意味着它需要两个 32 字节的插槽来存储其长度，然后是其值。
        • 总空间： 64 字节 + 32 字节（用于 tail(a)）= 128 或 十六进制的 0x80

  • 因此，head(b) = 0x80 —— 表示实际值 字符串 b 从参数块开始处偏移 128 字节处开始。

我们来看一下编码后的值，看看规则是否准确。

Method: 0189679b  ← 函数选择器 function selector for f(string,string)
------------
[000]: 0000000000000000000000000000000000000000000000000000000000000040  ← head(a): 指向 tail(a) 的偏移量，tail(a) 从字节 0x40 开始
[020]: 0000000000000000000000000000000000000000000000000000000000000080  ← head(b): 指向 tail(b) 的偏移量，tail(b) 从字节 0x80 开始
[040]: 000000000000000000000000000000000000000000000000000000000000000c  ← tail(a) 长度：12 字节
[060]: 4465636970686572436c75620000000000000000000000000000000000000000  ← tail(a) 数据：UTF-8 编码的“DecipherClub”，右填充为 32 字节
[080]: 000000000000000000000000000000000000000000000000000000000000000c  ← tail(b) 长度：12 字节
[0a0]: 4465636970686572436c75620000000000000000000000000000000000000000  ← tail(b) 数据：UTF-8 编码的“DecipherClub”，右填充为 32 字节

现在你已经理解了这一点，现在是时候玩一玩动态类型参数的编码了。

仅具有动态类型参数的函数

我们现在转向具有动态参数的函数，这就是头尾模型发挥作用的地方。

让我们来看一下这个函数：

    // argument - s = "DecipherClub"
    function encodeSecond(string memory s) public pure returns(bytes memory ){
        return msg.data;
    }

第 1 步：可视化头尾布局

让我们使用我们的标准模型写出逻辑结构：

encoded = [head(s)] [tail(s)]

因为只有一个参数，所以首先是它的 head，然后是它的 tail。

第 3 步：确定参数类型并编码值

参数 s 的类型为 string，它是 ABI 规范中的 动态类型。

动态类型是指大小 在编译时未知 的任何类型。在这种情况下，字符串 "DecipherClub" 的长度可能会有所不同，因此编译器无法提前确定其大小。

因为它是动态的，所以它的编码将遵循 头尾结构：

  • head 将存储一个指向数据开始位置的指针（偏移量）
  • tail 将存储实际内容（长度和数据）

现在我们将它分成两个部分：编码 head 和编码 tail。

第 3.a 步：编码 HEAD

按照 ABI 编码的基本规则，我们知道以下内容：

  • 每个参数 —— 静态或动态 —— 在 head 部分中都恰好分配了 32 字节
  • 对于动态类型，head 不 存储实际值，而是存储一个 偏移量，该偏移量告诉我们尾部（即实际值）从参数的开始处算起有多远

因此，你现在的任务是创建该偏移量：

回顾规则：

偏移量是从参数编码块的开始处开始测量的，而不是从完整 calldata 的开始处开始测量的。

在这种情况下：

  • head 占据了前 32 个字节
  • 只有一个参数，因此 tail 在 前 32 个字节之后立即开始
  • 因此，偏移量恰好是 32 字节 = 0x20（十六进制）

该值本身必须编码为 uint256，这意味着我们将 0x20 表示为一个左填充的 32 字节字：

head(s) = 0x0000000000000000000000000000000000000000000000000000000000000020

到目前为止，ABI 编码的值如下所示：

[head(s)] → 0x0000000000000000000000000000000000000000000000000000000000000020

这告诉 EVM：

“嘿，s 的实际数据从参数块开始后的 32 字节处开始。”

第 3.b 步：编码 TAIL

动态类型的 tail 包括两个组件：

  1. 数据的长度，以字节为单位
  2. 数据本身，填充到最接近的 32 字节边界
tail(s) = [长度][值][填充]

我们现在的任务是为我们给定的字符串值创建 tail，即 “DecipherClub”

**首先，让我们获取长度和编码

// 786 的编码值（第一个参数）
[000]: 0000000000000000000000000000000000000000000000000000000000000312
// 地址的编码值（第二个参数）
[020]: 0000000000000000000000005b38da6a701c568545dcfcb03fcb875f56beddc4
// 字符串 "DecipherClub" 的偏移量编码值（偏移量第三个参数）
[040]: 0000000000000000000000000000000000000000000000000000000000000060

步骤 3.b: 编码 TAIL

现在我们编码字符串 "DecipherClub" 的实际值。这与我们之前所做的完全相似。

  1. 获取编码后的字符串的长度
    1. “DecipherClub” 的编码值 - 0x4465636970686572436c7562
    2. 长度 - 12，或十六进制的 0xc。
  2. 创建 tail 布局
tail(c) = [length][value][padding]

// 长度为 0xc
000000000000000000000000000000000000000000000000000000000000000c
// 编码值为
4465636970686572436c75620000000000000000000000000000000000000000

最终的 Tail 部分变为

[060]: 000000000000000000000000000000000000000000000000000000000000000c
[080]: 4465636970686572436c75620000000000000000000000000000000000000000

步骤 4：组合所有内容以形成 ABI 编码的 Payload

现在我们组合：

[head(a)]
[head(b)]
[head(c)]
[tail(c)]

// 最终结果

 函数签名：0a4bef11
 ------------
 [000]: 0000000000000000000000000000000000000000000000000000000000000312
 [020]: 0000000000000000000000005b38da6a701c568545dcfcb03fcb875f56beddc4
 [040]: 0000000000000000000000000000000000000000000000000000000000000060
 [060]: 000000000000000000000000000000000000000000000000000000000000000c
 [080]: 4465636970686572436c75620000000000000000000000000000000000000000

可视化心智模型

这是一个可视化心智模型，用于使用上述规则对函数中的任何给定参数集进行编码。

考虑一个具有混合类型参数的简单函数：

function test( uint256 a, string b ) public {}

// arguments: a=2, b="DecipherClub"

现在，要按照规则编码这个函数，我们应该遵循这个流程：

img

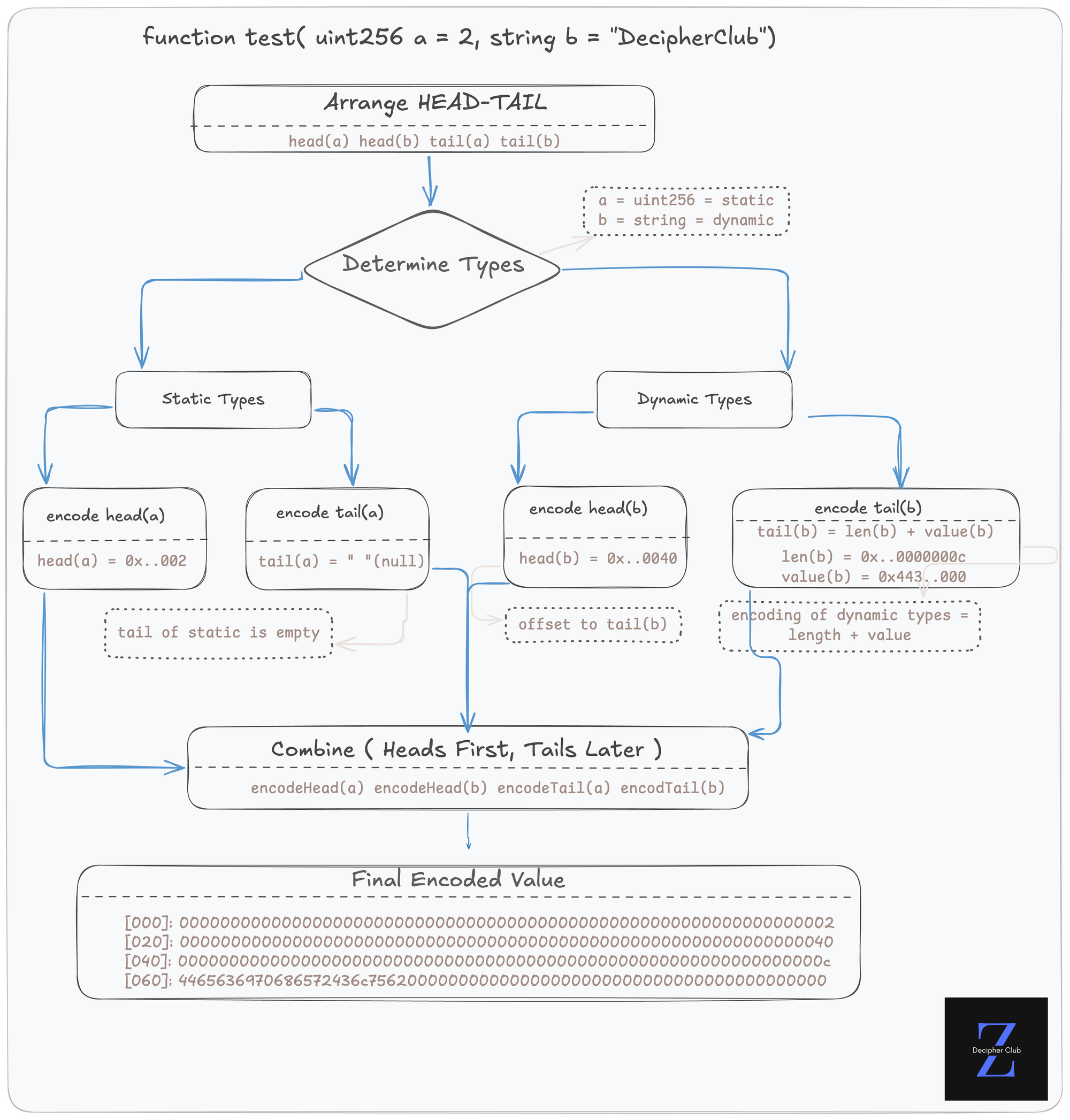
总结

在本系列的第一部分中，我们将 ABI 编码过程分解为其最精细的位和字节。我们还尝试了不同类型的编码的混合，包括两种类型。

这应该给你一个强大的心智模型来理解 ABI 编码的完整机制。阅读两次以更好地理解。

到目前为止，你应该能够自如地逐字节读取 ABI 编码的 payload，并理解编码后的数据如何映射回原始函数及其参数。更好的是，你应该能够在调用函数之前预测编码输出应该是什么样子。

在本系列的下一部分中，我们将更深入地研究，探索高级模式，例如结构体、数组、嵌套和复杂动态类型的编码。

干杯，解密者。

特别感谢 Owen Thurm（Guardian Audits 创始人）， Raoul（Runtime Verification 开发人员），Abhimanyu（Epoch Protoocl 联合创始人），Swayam（Inco network 开发人员），感谢他们的反馈和审查。

进一步阅读与参考

  1. Mastering ABI Encoding for Solidity and Ethereum
  2. Understanding ABI encoding for function calls
  3. Mastering Calldata
  4. Contract ABI Specification

有问题吗？

  • 原文链接： decipherclub.com/solidit...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
decipherclub
decipherclub
江湖只有他的大名，没有他的介绍。

decipherclub

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！