密码学血脉：Rabin家族

密码学传承：Rabin 家族

Tal 是她父亲的学术上的孙女

有许多著名的家族，兄弟姐妹跟随父母在计算机科学领域取得了世界领先的地位。这包括 Blum 家族 [ 这里] 和 Lenstra 家族 [ 这里]。所以，上周五，我很高兴能与一位世界领先者交谈，她追随了她父亲的脚步，她的父亲也是一位真正的世界领先者：Tal Rabin。她告诉我她的父亲——Michael O. Rabin——现在已经 93 岁了，而且她的两个女儿也追随她进入了计算机科学领域。

Tal 是宾夕法尼亚大学计算机与信息科学教授，也是 AWS 的主管。此前，她曾担任 Algorand 基金会的研究主管和 IBM 的 Thomas J Watson 研究中心的密码学研究主管。2014 年，她被 Business Insider 评为 22 位最有权势的女性工程师之一，并被 Anita Borg Institute 评为具有创新远见的女性。

2018 年，她被《福布斯》评为 美国科技界 50 强女性 之一，2019 年，她获得了 RSA 数学卓越奖。2023 年，她因在安全多方计算方面的工作而获得 Dijkstra 奖。Tal 的工作领域包括安全多方计算、阈值密码学、区块链系统和主动安全。

Michael O. Rabin 于 1931 年出生于德国。在 20 世纪 60 年代，他曾在加利福尼亚大学和麻省理工学院工作，然后晋升为哈佛大学教授。最终，在 1981 年，他成为希伯来大学的教授，并一直在那里工作。他完成了关于将大数分解为质数的著名工作。

Tal 和 Michael 都获得了 Dijkstra 奖 [ 这里]，他们是唯一获得该奖项的父子/女组合。这两个奖项都与 Michael Ben-Or 有关，他是 Tal 的导师，也是她父亲的博士生：

事实上，Tal 说，

我是我父亲学术上的孙女

而且，Tal 甚至和她的父亲一起发表了一篇经典论文 [ 这里]：

Rabin 与 Gary Miller 的合作

Michael 的一篇经典论文 [1] 基于 Gary Miller [2] 的工作：

该论文此后为 RSA 方法提供了生成素数的核心方法。通常，我们生成一个具有给定位数的奇数随机数，然后测试它是否为素数。如果不是，我们可以不断将该值加 2，直到达到素数。

Miller-Rabin 素性测试

Miller-Rabin 素性测试是 RSA 中用于测试素数的最流行方法之一。给定一个奇数 ( n)，我们将有一个奇数 ( n −1)，我们可以计算出 2 的幂，其值为 s，使得：

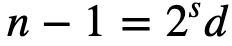
例如，如果 n 为 25，则 ( n −1) 将为 24，即 2×2×2×3，即 ²³×3。然后，我们选择一个介于 1 和 ( n −1) 之间的随机值 a。如果以下情况之一为真，我们可能得到一个素数：

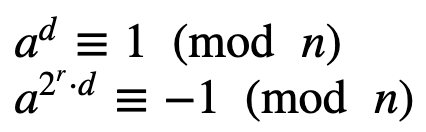
其中 r 是介于 0 和 s −1 之间的值。例如，如果我们取 n =61，则 ( n −1)=60。这可以表示为：²²×15，因此 s =2 且 d =15。让我们选择 a =5，所以我们得到：

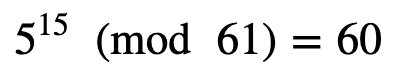
这没有通过第一个测试，所以让我们尝试：

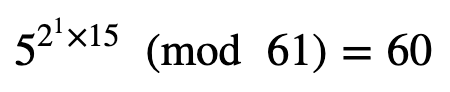
它等于 −1 (mod 61)。因此，它可能是一个素数。

现在我们将尝试 n =719，其中 ( n −1)=718。( n −1)=2×359，因此 s =1 且 d =359。让我们选择 a =7，所以第一个测试是：

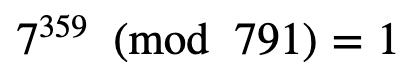
这起作用了，所以它可能是一个素数。让我们不要尝试 a =9：

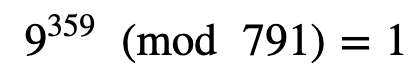
因此，我们有更多证据表明它是一个素数。

在 Miller-Rabin 测试中，我们执行 k 次试验。如果这些 trails 中的任何一个返回 false，则该值不是素数（而是合数）。如果它返回 true，它可能是素数。首先，我们有一个要测试的数字 ( n) 并生成一个随机数 ( a)，然后计算 d 来求解（其中 r 是大于 1 的值）：

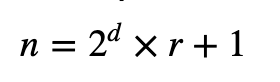
然后我们计算：

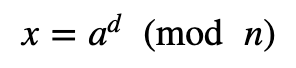
如果这是 1 或 -1，我们为素数返回一个真值。代码如下 [ 这里]：

while (true) {
var quotient = BigInteger.Divide(d,new BigInteger(2));
            var remainder=d % 2;
            if (remainder == BigInteger.One) {
                break;
            }
            s += 1;
            d = quotient;
        }
        var prime=false;
        if (BigInteger.ModPow(a,d,n)==1) {
            Console.WriteLine ("\nTest 1. It may be prime (a^d (mod n) = 1)");
            prime=true;
        }

接下来，我们不断对 x(mod n) 的值进行平方，而 d 的值小于 ( n −1) — 并且我们在每次测试中将 d 加倍。代码如下 [ 这里]：

var a=getRandom(n);
        var r=s-1;
        if (BigInteger.ModPow(a,BigInteger.Pow(2,r)*d,n)==(n-1)) {
            Console.WriteLine  ("\nTest 2. It may be prime (a^{2^r d} (mod n) == n-1)");
            prime =true;
        }

代码如下 [ 这里]：

namespace dotnet_rabin
{
using System.Numerics;
    using System.Reflection.Metadata;

class Program {
    public static BigInteger getRandom(BigInteger n){
        var length=n.GetBitLength()/8+1;

        Random random = new Random();
        byte[] data = new byte[length];
        random.NextBytes(data);
        var r=new BigInteger(data)%n;
        if  (r.Sign==-1) r=-r;
        if (r==0) r=2;
        return r;
    }
    static void Main(string[] args)
    {
        var nval="997";
        if (args.Length >0) nval=args[0];
        var n= BigInteger.Parse(nval);

        if (n == 2) {
            Console.WriteLine ("2");
            return;
        }

        if ((n % 2) == BigInteger.Zero) {
            Console.WriteLine ("{0} is not prime",n);
            return;
        }
        var s = 0;
        var d = n-1;

        while (true) {
            var quotient = BigInteger.Divide(d,new BigInteger(2));
            var remainder=d % 2;
            if (remainder == BigInteger.One) {
                break;
            }
            s += 1;
            d = quotient;
        }
        var a=getRandom(n);
        var r=s-1;
        Console.WriteLine ("(n-1)=({0}-1) = 2^{1} x {2}",n,s,d);
        Console.WriteLine ("s={0}, d={1}",s,d);
        Console.WriteLine ("a={0}, r={1}",a,r);
        var prime=false;
        if (BigInteger.ModPow(a,d,n)==1) {
            Console.WriteLine ("\nTest 1. It may be prime (a^d (mod n) = 1)");
            prime=true;
        }
        if (BigInteger.ModPow(a,BigInteger.Pow(2,r)*d,n)==(n-1)) {
            Console.WriteLine  ("\nTest 2. It may be prime (a^{2^r d} (mod n) == n-1)");
            prime =true;
        }
        if (prime==false)   Console.WriteLine ("{0} is not a prime",n);
        else   Console.WriteLine ("{0} is a prime",n);
    }
}
}

一个示例运行是 [ 这里]：

(n-1)=(19-1) = 2^1 x 9
s=1, d=9
a=7, r=0

Test 1. It may be prime (a^d (mod n) = 1)
19 is a prime

这里有一些例子可以尝试：

• 尝试 19？。 尝试
• 尝试 21？。 尝试
• 尝试 27？。 尝试
• 尝试 31？。 尝试
• 尝试 33？。 尝试
• 尝试 53？。 尝试
• 7919 是素数吗？。 尝试
• 858,599,509 是素数吗？。 尝试
• 982,451,653 是素数吗？。 尝试
• 982,451,652 是素数吗？。 尝试
• 643808006…,153 是素数（210 位数）吗？。 尝试
• 643808006…,152 是素数（210 位数）吗？。 尝试
• 4494179990..,163 是素数（210 位数）吗？。 尝试
• 4494179990..,162 是素数（210 位数）吗？。 尝试
• 23097…426570593 是素数（210 位数）吗？。 尝试
• 23097…426570595 是素数（210 位数）吗？。 尝试
• 5521712….5385789993 是素数（220 位数）吗？。 尝试
• 56125680…531131327771 是素数（230 位数）吗？。 尝试
• 6413528947 … 3367 是素数（125 位数）吗？ RSA-250 的素数之一，应该是素数。 尝试
• 333720275949781565 … 062711 是素数（125 位数）吗？ RSA-250 的素数之一，应该是素数。 尝试
• 214032465024074 … 5937497937 是素数（250 位数）吗？ 这是 RSA-250 的公共模数，不应该是素数（因为 p × q）。 尝试

Rabin 公钥方法

使用 Rabin 公钥 [3]，我们选择两个素数（ p 和 q）。如果可能， p ≡ q ≡3 (mod4) 简化了解密过程。最初我们确定 n = p ⋅ q，其中 n 是公钥，p 和 q 是私钥。我们用 n 加密，用 n 的因子 p 和 q 解密。这是一个例子：

Rabin 公钥 - asecuritysite.com

结论

我非常期待与 Tal 聊天，敬请关注完整的采访。

参考文献

[1] Rabin, M. O. (1980). Probabilistic algorithm for testing primality. Journal of number theory, 12(1), 128–138.

[2] Miller, G. L. (1976). Riemann’s hypothesis and tests for primality. Journal of computer and system sciences, 13(3), 300–31

[3] Rabin, M. O. (1979). Digitalized signatures and public-key functions as intractable as factorization (No. MIT/LCS/TR-212). Massachusetts Inst of Tech Cambridge Lab for Computer Science [ paper].

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～