ZNARKs：整数SNARKs

XPTY
发布于 2024-11-11 12:40
阅读 29

SNARK总是要用于有限域上的计算吗？并不是。

>原文： https\://www\.zksecurity.xyz/blog/posts/znarks/
>作者：Mathias Hall-Andersen
>译者：Kurt Pan

SNARK 总是要用于有限域上的计算吗？并不是。

今天，我们将探讨我们最近的预印本《Fully-Succinct Arguments over the Integers from First Principles》中提出的技术，这篇论文研究了整数电路上的 SNARK 构造，提供了一种简单但新颖的方法来构造高效的证明系统来进行涉及整数的计算，同时避开了处理整数的大多数常见复杂情况。该技术使我们能够使用新工具：_带模余数的多项式承诺_，将现有的（多线性）SNARK“编译”为整数上的论证。

- https://eprint.iacr.org/2024/1548

## 应用

现有的 SNARK（通常）是为有限域上的计算而设计的： 电路或程序在有限域上执行的可满足性。 一些工作还探索了其他有限环，通常为$\mathbb{Z}_{2^k}$即$k$比特整数上的 SNARK。这两种情况都意味着计算中的每个值都具有**先验有限的有界大小**。在最近的工作中，我们引入了首个（完全简洁的）用于**整数上计算**的 SNARK：整数上的 SNARK 允许电路赋值（或在是程序情况下中的内存）可以采用$\mathbb{Z}$中的任意值，**无论计算中的值有多大**，证明仍然是可靠且简洁的。

整数上的计算有许多潜在有趣的应用，包括模拟（甚至非常小的）素域。我们博客的读者应该都很清楚适用于有限域的所有电路“技巧”，但可能不太熟悉整数上的计算/电路，让我们首先探索一些整数上的 SNARK 的应用示例，这可能会很有用。

### 使用平方和高效进行范围检查

对整数的范围检查并不需要将值分解为比特，这意味着范围检查的开销与范围的大小无关。诀窍在于观察到所有的非负整数都可以表示为四个平方之和, 换句话说, 对于任意$n \geq 0$证明者可以（高效地）找到$a,b,c,d$使得:
							$n = a^2 + b^2 + c^2 + d^2$

使用这种技术，你可以通过证明你知道$a_1,b_1,c_1,d_1$和$a_2,b_2,c_2,d_2$满足下式来证明$n \in [0,B]$:
							$n = a_1^2 + b_1^2 + c_1^2 + d_1^2$
						$B - n = a_2^2 + b_2^2 + c_2^2 + d_2^2$

换句话说, $n \geq 0$且$B - n\geq 0$。这是可以优化的，Couteau、Peters 和 Pointcheval证明了$n \in [low,high]$等价于存在$a,b,c$使得:
						$4·(n - low)·(high - n) + 1 = a^2 + b^2 + c^2$

因此你可以用 4 个 R1CS 约束或1个 PlonKish 门的常数开销来进行范围检查。

### 高效的混合域模拟

我们可以非常容易地在整数电路中的模拟素域：值$\overline x \in \mathbb{F}_p$可以表示使得$x \equiv \overline x\mod p$的整数$x \in \mathbb{Z}$。给定两个值$x,y \in \mathbb{Z}$, 我们可以将他们的乘积约束为$z \equiv x·y \mod p$，通过要求:
							$z = x·y - q·p$

对某个证明者选择的$q \in \mathbb{Z}$。对加法也是类似的。请注意，我们并不要求证明者完全约减结果，因为没有"模数去溢出"，即使证明者使用等价类的一个大的代表元，电路也会正确运行：只是让自己的一切都变得更慢了。如果需要唯一的代表元，你可以简单地使用上面的（非常高效的）范围检查来检查$z \in [0,p-1]$。

这甚至允许去模拟"动态"选择的域$\mathbb{F}_p$，比如在$p$作为公共输入提供的时候。还允许用相同数量约束去模拟任意大小的域，以及在同一电路中模拟任意数量的不同域（并在它们之间切换）。

### 验证 RSA 群中的计算

在上面的例子中, 我们选择的模数$p$是质数, 但对于合数模数$N$, 例如 RSA 模数$N = p·q$，同样适用。这可以使得验证整数电路内的 RSA 签名和 RSA 累加器非常高效。

### 一个智力上的好奇：$\mathbb{Q}$-电路

使用一个对$\mathbb{Z}$的证明系统去证明关于有理数$\mathbb{Q}$的陈述是比较容易的：我们将有理数表示为整数对$(n,d)$，代表分数$n/d$。只要有需要，我们就可以通过强制$d·sign \in [1,\infty)$$来约束 ，对某个由证明者选择的$ $sign \in \mathbb{Z}$ ，并使用"平方和"技术来约束范围检查。注意许多非零检查都可以通过计算$d_1·d_2·...·d_n$并约束乘积非零来进行批处理。

为了约束分数乘积$n_1/d_1·n_2/d_2 = n_3/d_3$，可以要求:
							$n_3 = n_1·n_2$
							$d_3 = d_1·d_2$
除法可以类似地约束:
							$n_3 = n_1·d_2$
							$d_3 = d_1·n_2$

相等可以通过下式约束来检查：
							$d_1·n_2 = d_2·n_1$

最难的部分是分数和，它需要一个公分母:
							$n_3 = n_1·f_1 + n_2·f_2$
							$d_3 = d_1·f_1$
							$d_1·f_1 = d_2·f_2$
							$f_1 \neq 0$
							$f_2 \neq 0$

对由证明者选择的$f_1,f_2$。

我不知道$\mathbb{Q}$-电路有任何实际用途 , 但有趣的是, 你可以有一个为特征为零的域设置的 SNARK。

## 绕道：指纹识别

在我们进入如何为整数构造 SNARK 的细节之前, 让我们先看一下"指纹识别"技术：假设你有一个整数上的电路$C$, 由具有扇入2和任意扇出的加法门和乘法门组成。比如说，可能看起来像这样:

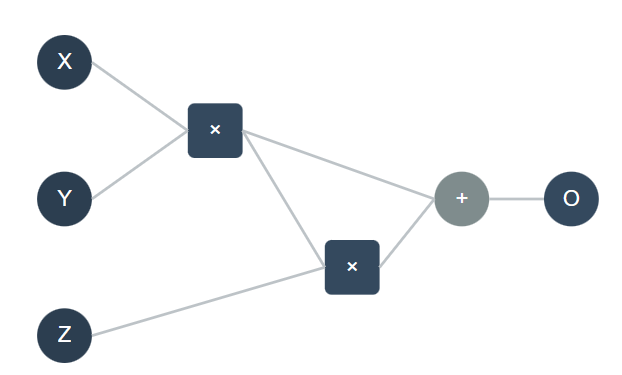
![image.png](https://img.learnblockchain.cn/attachments/2025/04/CZBx19P96811cd6b58e8a.png)

假设你想让某人相信你知道见证$\omega = (X,Y,Z)$使得$C(\omega) = 0$。对于上面的电路，一个简单的协议就足够了：证明者只需发送$\omega$，验证者检查$C(\omega) = 0$。

但请注意，乘法会增加电路内部值的大小：乘积$(X·Y)·Z$的大小是$X,Y$和$Z$大小的和。事实上, 因为可以在电路的每一层连续乘以中间结果, 所以内部值的大小会随着电路的深度呈指数增长。例如，计算$x^{2^k}$的电路有深度$k$，在每一层计算$x^2 = x^{2^{-1}}·x^{2^{-1}}$，但$x^{2^k}$大小为$O(2^k·|x|)$。因此, 直接验证电路的计算仅适用于小深度的电路......

我们可以做得更好吗?当然可以！即使用一种称为"指纹识别"的技术，该技术依赖于随机性。Sanjeev Arora 和 Boaz Barak 在《计算复杂性：一种现代方法》一书中描述了该技术。想法非常简单，不是天真地重新计算电路，在收到见证$\omega$后验证者选择一个随机素数$p$并计算电路模$p$。如果结果为零, 则验证者确信见证是正确的。

稍微非形式化地写做:
				$$\Pr_{p}\big[C(w,x) \bmod p = 0\big] > \epsilon \Leftrightarrow C(w,x) = 0$$
为什么可以这样? 假设$y = C(x,\omega)$且$y \neq 0$, 即电路不满足, 但使验证者相信它是满足的。 $y$的最大值为：
						$$|y| \le \max\{|x|, |w|\}^{2^{d}}$$

其中$d$是电路的深度。现在$y = 0\mod p$当且仅当 $p$整除$y$。有多少个不同的素数可以整除$y$? 嗯, 非常粗略的估计会小于$\log_2(y)$。此外, 大致还有$B/(\log B)$个素数小于$B$。所以我们选择$B$使得
			$$\frac{B}{\log B} \cdot \frac{1}{\log_2 (y)} < \frac{B}{\log B} \cdot \frac{1}{\log_2 (\max\{|x|, |w|\}) \cdot 2^d} < \epsilon$$

那么为了使$\epsilon$（非常）小，我们的随机素数$p$应该取多大？

从上面的等式可以清楚地看出，如果我们选择$B \gg 2^d$，那么$\epsilon$会很小。换句话说，素数的大小需要大致与电路的（乘法）_深度_呈正比。

### 呈指数级缩减

我们论文中的关键想法是通过使电路仅具有常数深度来“缩小”这个想法。幸运的是，常数深度电路是 ZK 证明系统中的常态：通过引入新变量，更大深度的电路可以被扁平化为常数深度电路，例如，检查 R1CS 关系的电路具有乘法深度一。

素数的使用使我们能够使用现有的 SNARK 技术高效地证明电路的可满足性，因为_我们只需证明电路在素域上的可满足性_。

## 具有模余数的多项式承诺

在上一节中，验证者收到了来自证明者的整个见证$\omega \in \mathbb{Z}^n$。这是一个问题：我们在尝试构造一个 SNARK，我们希望通信规模较小。解决方案是让证明者承诺$\omega$并向我们发送承诺。

因为我们之后需要计算"$C(\omega)\mod p$", 对多线性多项式$f(X_1,...,X_k) \in \mathbb{Z}[X_1,...,X_n]$有一个多项式承诺方案是有用的，可以在一点$x_1,...,x_k$模任意素数$p$处打开多项式 ，表明:
						$y = f(x_1,...,x_k)\mod p$

关键是你可以在承诺多项式之后再选择$p$。这与通常的多项式承诺方案不同，在通常的多项式承诺方案中，素数在承诺时是固定的。这个新的原语显然比通常的多项式承诺方案更强大：你总是可以固定一个素数$p$- 在这种情况下, 你就有了一个常规的多项式承诺方案。

## aratan

> 至于海龟，它体型巨大，船上的人都把它当成一座岛屿。一位商人报告说："发现了一座从海中升起的长满绿色植物的岛屿，我们上岸挖坑生火，岛屿开始移动，水手们说："回到船上！这是一只乌龟！大火把他吵醒了，我们就要迷路了！" '
> 
> - Zakariya al-Qazwini 《动物之书》 (13 世纪)
>

Zaratan 是我们新的整数 SNARK。它将由类似 DARK 的技术构造的具有模余数的多项式承诺与素域上的标准多线性 SNARK（在我们的例子中是 Spartan） 相结合。

由于技术原因，我们不能将我们的构造基于DARK 承诺：DARK 承诺仅对有理函数类$f(X_1,...,X_k)/N$，$N$是一个小整数，具有绑定性质 。这对于有限域上的SNARK 来说没问题，因为$N^{-1}\mod p$是一个域元素（除非$p|N$），这意味着$f(X_1,...,X_k)/N \mod p$是域上的多项式，但这对于我们的应用来说不够，因为我们需要它是整数上的多项式。相反，我们需要从Block 等人的效率低得多的多项式承诺方案中导出一个方案。

然而，由于我们需要的是具有模余数的多线性多项式承诺方案来编译标准现有的多线性 SNARK（例如 Spartan 或 HyperPlonk），因此我们对如何从非常不同的技术创造更高效的实例化已经有了一些想法。所以敬请期待！

原文： https\://www.zksecurity.xyz/blog/posts/znarks/ 作者：Mathias Hall-Andersen 译者：Kurt Pan

SNARK 总是要用于有限域上的计算吗？并不是。

今天，我们将探讨我们最近的预印本《Fully-Succinct Arguments over the Integers from First Principles》中提出的技术，这篇论文研究了整数电路上的 SNARK 构造，提供了一种简单但新颖的方法来构造高效的证明系统来进行涉及整数的计算，同时避开了处理整数的大多数常见复杂情况。该技术使我们能够使用新工具：带模余数的多项式承诺，将现有的（多线性）SNARK“编译”为整数上的论证。

https://eprint.iacr.org/2024/1548

应用

现有的 SNARK（通常）是为有限域上的计算而设计的：电路或程序在有限域上执行的可满足性。一些工作还探索了其他有限环，通常为$\mathbb{Z}_{2^k}$即$k$比特整数上的 SNARK。这两种情况都意味着计算中的每个值都具有先验有限的有界大小。在最近的工作中，我们引入了首个（完全简洁的）用于整数上计算的 SNARK：整数上的 SNARK 允许电路赋值（或在是程序情况下中的内存）可以采用$\mathbb{Z}$中的任意值，无论计算中的值有多大，证明仍然是可靠且简洁的。

使用平方和高效进行范围检查

使用这种技术，你可以通过证明你知道$a_1,b_1,c_1,d_1$和$a_2,b_2,c_2,d_2$满足下式来证明$n \in [0,B]$: $n = a_1^2 + b_1^2 + c_1^2 + d_1^2$ $B - n = a_2^2 + b_2^2 + c_2^2 + d_2^2$

因此你可以用 4 个 R1CS 约束或1个 PlonKish 门的常数开销来进行范围检查。

高效的混合域模拟

验证 RSA 群中的计算

一个智力上的好奇：$\mathbb{Q}$-电路

使用一个对$\mathbb{Z}$的证明系统去证明关于有理数$\mathbb{Q}$的陈述是比较容易的：我们将有理数表示为整数对$(n,d)$，代表分数$n/d$。只要有需要，我们就可以通过强制$d·sign \in [1,\infty)$$来约束，对某个由证明者选择的$ $sign \in \mathbb{Z}$ ，并使用"平方和"技术来约束范围检查。注意许多非零检查都可以通过计算$d_1·d_2·...·d_n$并约束乘积非零来进行批处理。

为了约束分数乘积$n_1/d_1·n_2/d_2 = n_3/d_3$，可以要求: $n_3 = n_1·n_2$ $d_3 = d_1·d_2$ 除法可以类似地约束: $n_3 = n_1·d_2$ $d_3 = d_1·n_2$

相等可以通过下式约束来检查： $d_1·n_2 = d_2·n_1$

最难的部分是分数和，它需要一个公分母: $n_3 = n_1·f_1 + n_2·f_2$ $d_3 = d_1·f_1$ $d_1·f_1 = d_2·f_2$ $f_1 \neq 0$ $f_2 \neq 0$

对由证明者选择的$f_1,f_2$。

我不知道$\mathbb{Q}$-电路有任何实际用途 , 但有趣的是, 你可以有一个为特征为零的域设置的 SNARK。

绕道：指纹识别

稍微非形式化地写做: $$\Pr_{p}\big[C(w,x) \bmod p = 0\big] > \epsilon \Leftrightarrow C(w,x) = 0$$ 为什么可以这样? 假设$y = C(x,\omega)$且$y \neq 0$, 即电路不满足, 但使验证者相信它是满足的。 $y$的最大值为： $$|y| \le \max{|x|, |w|}^{2^{d}}$$

其中$d$是电路的深度。现在$y = 0\mod p$当且仅当 $p$整除$y$。有多少个不同的素数可以整除$y$? 嗯, 非常粗略的估计会小于$\log_2(y)$。此外, 大致还有$B/(\log B)$个素数小于$B$。所以我们选择$B$使得 $$\frac{B}{\log B} \cdot \frac{1}{\log_2 (y)} < \frac{B}{\log B} \cdot \frac{1}{\log_2 (\max{|x|, |w|}) \cdot 2^d} < \epsilon$$

那么为了使$\epsilon$（非常）小，我们的随机素数$p$应该取多大？

从上面的等式可以清楚地看出，如果我们选择$B \gg 2^d$，那么$\epsilon$会很小。换句话说，素数的大小需要大致与电路的（乘法）_深度_呈正比。

呈指数级缩减

素数的使用使我们能够使用现有的 SNARK 技术高效地证明电路的可满足性，因为我们只需证明电路在素域上的可满足性。

具有模余数的多项式承诺

aratan

至于海龟，它体型巨大，船上的人都把它当成一座岛屿。一位商人报告说："发现了一座从海中升起的长满绿色植物的岛屿，我们上岸挖坑生火，岛屿开始移动，水手们说："回到船上！这是一只乌龟！大火把他吵醒了，我们就要迷路了！" '

Zakariya al-Qazwini 《动物之书》 (13 世纪)

Zaratan 是我们新的整数 SNARK。它将由类似 DARK 的技术构造的具有模余数的多项式承诺与素域上的标准多线性 SNARK（在我们的例子中是 Spartan）相结合。

由于技术原因，我们不能将我们的构造基于DARK 承诺：DARK 承诺仅对有理函数类$f(X_1,...,X_k)/N$，$N$是一个小整数，具有绑定性质。这对于有限域上的SNARK 来说没问题，因为$N^{-1}\mod p$是一个域元素（除非$p|N$），这意味着$f(X_1,...,X_k)/N \mod p$是域上的多项式，但这对于我们的应用来说不够，因为我们需要它是整数上的多项式。相反，我们需要从Block 等人的效率低得多的多项式承诺方案中导出一个方案。