ZK友好的哈希函数

引言

哈希函数

一个 加密哈希函数↗ 是密码学的基本原语之一。（在本文中，除非另有说明，否则哈希函数将指代加密哈希函数。）加密哈希函数满足以下三个安全性质：

1. 前像抗性：给定哈希值 hhh，找到任何输入消息 mmm 使得 f(m)=hf(m)=h 是困难的。
2. 第二前像抗性：给定输入消息 mmm，找到消息 m′(≠m)m'(\neq m) 使得 f(m′)=f(m) 是困难的。
3. 碰撞抗性：找到任何两个不同的输入消息 m1,m2(≠m1)m_1,m_2(\neq m_1)是困难的，使得 f(m1)=f(m2)。

加密方案如数字签名、消息认证码、承诺方案和身份验证都建立在哈希函数之上。例如，哈希函数的前像抗性属性使得 工作量证明↗ 系统在加密货币中得以实现。SHA-2 和 SHA-3 是常见的哈希函数示例，它们被用于一般用途。

哈希在 ZK 协议中的使用

哈希函数在 ZK 协议中也非常有用。一个著名的例子是在 Merkle 树中的成员资格检查。对于 Merkle 根 rrr，证明者将声称知晓见证 w1,…,wnw_1,\dots,w_n，使得

H(…H(H(w1,w2),w3))…,wn)=rH(\dots H(H(w_1,w_2),w_3))\dots,w_n)=rH(…H(H(w1​,w2​),w3​))…,wn​)=r

以证明他们对元素 w1w_1 的知识，w1 是 Merkle 树中的成员。我们在之前的文章 “Tornado Cash 是如何工作的？” 中讨论了这种用法。

传统的哈希函数的使用也可以应用于 ZK 协议，例如，利用原生哈希计算进行完整性检查、从固定长度种子获取伪随机字符串，以及签署交易等。

为什么需要 ZK 友好的哈希函数？

标准化的哈希函数如 SHA-2 和 SHA-3 已进行了深入研究，并且其安全性被广泛认为是可靠的。此外，与其竞争对手相比，它们的传统软件和硬件实现的效率也较高。

因此，当我们需要在 ZK 协议中评估哈希时，似乎很好地使用 SHA-2 或 SHA-3。然而，许多 ZK 协议使用相对不太熟悉的哈希函数，如 MiMC↗、Poseidon↗ 和 Rescue↗，而不是 SHA-2 和 SHA-3。

主要原因在于 ZK 协议中的效率是通过与传统度量（如运行时间、功耗和门计数）截然不同的方式来决定的。ZK 协议中电路的效率取决于它们的代数结构。

通常，如果电路可以用大型域中的简单表达式表示，那么它将在证明者执行时间和证明大小上允许高效的证明。不幸的是，传统哈希函数并不适合此情况。

例如，在 zk-STARK 中计算哈希时，SHA-2 比 ZK 友好的哈希函数效率低大约 50–100 倍。这一巨大的性能差距表明了对 ZK 友好哈希函数的需求。

在本文中，我们将介绍在著名会议和期刊中提出的几种 ZK 友好的哈希函数。关注每个哈希函数的设计原理可能会很有趣。

ZK 协议

我们首先讨论 ZK 协议。在试图充分理解协议的基础上，我们将重点关注它们的高层特征以及确定效率的指标。

zk-SNARK

zk-SNARK 是一个缩写，代表 零知识简洁 非交互式知识证明。

1. 零知识：验证者获取的信息仅限于声明是真的。
2. 简洁：证明大小和验证者时间是 亚线性 的。
3. 非交互式：证明者和验证者之间没有任何交互。
4. 知识证明：不仅证明输入 xxx 存在，还证明证明者知道 xxx。

虽然存在几种方式来构建满足上述特征的协议，如 线性 PCP + 配对加密↗、常数回合多项式 IOP↗ 和 多项式承诺方案 + IOP 基础↗，但基于线性 PCP 和配对加密的 Groth16↗ 是最广泛使用的协议。

Groth16 和许多其他零知识证明系统，如 Aurora↗、Ligero↗ 和 Bulletproofs↗ 都是在 Rank-1 Constraint System (R1CS) 形式下评估电路的。

R1CS 示例

R1CS 是一个方程系统，其中每个方程由一个三元组 (a⃗i,b⃗i,c⃗i)(\vec{a}_i,\vec{b}_i,\vec{c}_i)(ai​,bi​,ci​) 定义，使得 (a⃗i⋅s⃗)×(b⃗i⋅s⃗)=(c⃗i⋅s⃗)(\vec{a}_i \cdot \vec{s}) \times (\vec{b}_i \cdot \vec{s}) = (\vec{c}_i \cdot \vec{s})(ai​⋅s)×(bi​⋅s)=(ci​⋅s)。

例如，y=x3y = x^3 是由三元组（中间值 z=x2z = x^2）定义的两个方程：

x×x=z:((100)⋅(xyz))×((100)⋅(xyz))=((001)⋅(xyz)),x \times x = z : \left( \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} \right) \times \left( \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} \right) = \left( \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} \right),x×x=z:​​100​​⋅​xyz​​​×​​100​​⋅​xyz​​​=​​001​​⋅​xyz​​​,z×x=y:((001)⋅(xyz))×((100)⋅(xyz))=((010)⋅(xyz)).z \times x = y : \left( \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} \right) \times \left( \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} \right) = \left( \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} \right).z×x=y:​​001​​⋅​xyz​​​×​​100​​⋅​xyz​​​=​​010​​⋅​xyz​​​。

在 SNARK 设置中，成本由 R1CS 中的约束数量决定。例如，xαx^\alphaxα 对于常数 α\alphaα 需要约 ⌈log⁡2(α)⌉\lceil \log_2(\alpha) \rceil⌈log2​(α)⌉ 的约束。

zk-STARK

zk-STARK 是一个缩写，代表 零知识可扩展 透明知识证明。

1. 零知识：验证者获取的信息仅限于声明是真的。
2. 可扩展：证明者的时间是 准线性的；证明大小和验证者时间是 亚线性 的。
3. 透明：不需要可信的设置。
4. 知识证明：不仅是输入 xxx 存在，还有证明者知道 xxx。

任何满足上述条件的协议称为 zk-STARK。然而，zk-STARK 通常指的是在 论文↗ 中首次提出的协议。我们在本文中也将该论文中的协议称为 zk-STARK。

为了在 STARK 环境中评估电路，该电路应转化为 代数中间表示 (AIR)。

AIR 示例

我们给出计算 Fibonacci 序列的一个示例。Fibonacci 序列定义为 a0=1,a1=1,a_0 = 1, a_1 = 1,a0​=1,a1​=1，且 ai=ai−1+ai−2 当 i≥2a_i = a_{i-1} + a_{i-2} \text{ for } i \geq 2ai​=ai−1​+ai−2​ 当 i≥2。

证明者希望证明 a7=21a_{7} = 21a7​=21。然后，一个 代数执行轨迹 (AET)，即 Fibonacci 序列计算的执行轨迹为：

而在多项式形式中描述的 AIR 约束有：

1. a0−1=0,a_0 -1 = 0,a0​−1=0,
2. a1−1=0,a_1 -1 = 0,a1​−1=0,
3. ai−ai−1−ai−2=0 对于 2≤i≤7,a_{i} - a_{i-1} - a_{i-2} = 0 \text{ for } 2 \leq i \leq 7,ai​−ai−1​−ai−2​=0 对于 2≤i≤7,
4. a7=21.a_7 = 21.a7​=21。

设 ttt 为行数，www 为 AET 中的列数。那么 AET 的大小为 t⋅wt \cdot wt⋅w。此外，设 ddd 为 AIR 约束的最大度数。在我们的例子中，t=8,w=1,d=1t = 8, w = 1, d = 1t=8,w=1,d=1。ZK-STARK 的效率由 t,w,dt, w, dt,w,d 决定。对于每个电路，通过测量 t⋅w⋅dt \cdot w \cdot dt⋅w⋅d 来比较效率。

ZK 友好的哈希函数

大致来说，给定电路的代数表示越简单，对于 R1CS 和 AIR 表示的效率越高。因此，加密学家开始设计既在代数上简单又安全的结构。我们通常将这些密码称为 面向算术的密码 (AOCs)。

对于 AOCs，大多数传统的对称密钥密码分析（如差分分析和线性分析）通常相关性较弱。对于 AOCs 最强大的攻击类型是代数攻击，例如 Gröbner 基、线性化、GCD 和插值攻击。一旦设计者决定了他们密码的设计，回合数就会被选择得足够安全以抵御这些攻击。

另一方面，这个领域相对较新，并且出现了有趣的攻击（见 示例一个↗、 示例二↗、 示例三↗ 和 示例四↗），这些攻击常常导致密码破坏或参数修改，不过我们将在下一篇文章中讨论这些内容。

让我们看一下不同 AOCs 的设计原理。

MiMC

MiMC↗ 是第一个 ZK 友好的哈希函数，首次在 ASIACRYPT 2016 中提出。尽管在 MiMC 之后提出了更有效的 ZK 友好哈希函数，但 MiMC 在许多应用中仍然被广泛使用，因为与其他 ZK 友好哈希函数相比，它被认为是成熟的。

MiMC 的设计极其简单：函数 F(x):=x3F(x) := x^3F(x):=x3 与子密钥加法迭代进行。这一概念已在 1990 年代由 Nyberg 和 Knudsen 提出，称为 KN-Cipher↗。

MiMC-n/nn/nn/n

我们首先看一下一个块密码。块密码通过迭代 rrr 轮构造，其中每轮函数描述为 Fi(x)=(x+k+ci)3F_i(x) = (x + k + c_i)^3Fi​(x)=(x+k+ci​)3。在轮函数中，cic_ici​ 是一个轮常数，kkk 是一个密钥，字段为 Fq\mathbb F_qFq​，其中 qqq 是一个大素数或 q=2nq = 2^nq=2n。加密过程定义为

Ek(x)=(Fr−1∘Fr−2∘⋯∘F0)(x)+k.E_k(x) = (F_{r-1} \circ F_{r-2} \circ \dots \circ F_0)(x) + k.Ek​(x)=(Fr−1​∘Fr−2​∘⋯∘F0​)(x)+k。

并且 c0c_0c0​ 固定为 000，因为 c0c_0c0​ 不影响安全性。（如果你有兴趣，我建议你自己查阅！）

对于域 Fq\mathbb F_qFq​，F(x)=x3F(x) = x^3F(x)=x3 的逆只有当且仅当 gcd⁡(3,q−1)=1\gcd(3, q-1) = 1gcd(3,q−1)=1。为此，作者建议选择奇数 nnn 对于 q=2nq = 2^nq=2n 和 q=3k+2q = 3k+2q=3k+2 的质数 qqq。

轮常数 cic_ici​ 在论文中并未具体说明，但推荐将其初始随机选择然后硬编码到实现中。为了展示在轮常数上 没有藏私↗，常常选取从某些消息的 SHA-2（或任何其他安全哈希函数）摘要生成，如 MiMC0、MiMC1，…\dots….

轮数决定为 r=⌈log3q⌉r = \lceil log_3 q \rceil r=⌈log3​q⌉。例如，对于域 F_2127\mathbb F\_{2^{127}}F_2127，轮数 r=⌈log3(2127)⌉=81r = \lceil log_3 (2^{127}) \rceil = 81r=⌈log3​(2127)⌉=81。关于此的原因我们稍后会讨论。

rrr 轮的 MiMC-n/nn/nn/n。图片来自 MiMC 论文。

MiMC-2n/n2n/n2n/n

使用相同的非线性置换在 Feistel 网络中构造块密码也是可能的。MiMC-2n/n2n/n2n/n 的轮函数在下面图示中描述，可以定义为：

xL∥xR←xR+(xL+k+ci)3∥xL.x_L \| x_R \leftarrow x_R + (x_L + k + c_i)^3 \| x_L.xL​∥xR​←xR​+(xL​+k+ci​)3∥xL​。

MiMC-2n/n2n/n2n/n 轮函数。图片来自 这里↗。

对于每个轮，只改变一半的数据；因此，Feistel 版本的轮数是 2⋅⌈log3q⌉2 \cdot \lceil log_3 q \rceil 2⋅⌈log3​q⌉，相对于 MiMC-n/nn/nn/n 的轮数翻倍。

哈希函数

当密钥固定为 000 时，块密码变成一个置换。给定一个置换，有一个著名的构造方法可以从置换导出哈希函数，称为 海绵框架↗，该构造方法已被证明是安全的，并且在许多其他哈希函数中使用，包括 SHA-3↗。

海绵构造。PiP_iPi​ 是输入；ZiZ_iZi​ 是哈希输出。未使用的 容量 ccc 应为所需碰撞或前像攻击的两倍。图片来自 维基百科↗。

海绵构造由名为 吸收 和 挤压 的两个阶段组成。在吸收阶段，输入数据被吸收到海绵中。之后，结果被挤出来。

MiMC 的哈希函数同样基于海绵框架。在吸收阶段，消息块添加到状态的一个子集中，然后使用某个置换函数 fff（在我们的情况中，是 MiMC 置换）整体进行转换。请注意，在本文中介绍的所有其他 ZK 友好的哈希函数也都是基于海绵框架的。

安全分析

虽然论文中考虑了插值攻击、GCD 攻击、不变子场攻击、差分密码分析和线性密码分析，但我们仅在这里介绍插值攻击，它提供了轮数的下限。插值攻击在没有了解密钥的情况下构造对应于加密函数的多项式。如果对手能够构造出这样的多项式，那么对于任何给定的明文，都可以在不知道密钥的情况下生成对应的密文。

设 EkE_kEk​ 是一个关于输入 xxx 的加密函数，度数为 ddd。那么通过 d+1d+1d+1 个明文-密文对，Ek(x)E_k(x)Ek​(x) 可以根据拉格朗日定理构造，并且构造拉格朗日插值多项式的复杂度为 O(dlog⁡d)O(d \log d)O(dlogd)。在我们的案例中，度数 d=3rd = 3^rd=3r。通过选择 r=⌈log3q⌉r = \lceil log_3 q \rceil r=⌈log3​q⌉，度数 ddd 达到 q−1q - 1q−1 并且攻击变得不可行。

SNARK 复杂度

由于单个约束可以平方值，因此在每轮 MiMC 置换中有两个 R1CS 约束：

x2 = x*x
x3 = x2*x

为了生成一个 256 位输出哈希（输入为 256 位 xxx），使用海绵构造。具体地，计算 (x,0)(x,0)(x,0) 的 MiMC-2n/n2n/n2n/n，然后剩下的 256 位是哈希值。轮数选择为 2⋅⌈log3(2256)⌉=3242⋅⌈log3​(2256)⌉=324。然后约束的数量为 324×2=628324×2=628。注意该领域应选择 gcd⁡(3,q−1)=1\gcd(3, q-1) = 1gcd(3,q−1)=1，这意味着 F_2256\mathbb F\_{2^{256}}F_2256 不应被选择。

STARK 复杂度

在 AIR 表示中，对于 MiMC-2n/n2n/n2n/n，每行有两个变量，xLx_LxL​和 xRx_RxR​。我们在第 iii 行中表示 xL,xRx_L, x_RxL(i),xR(i)x^{(i)}_L,x^{(i)}_R。则根据轮函数 xL∥xR←xR+(xL+k+ci)3∥xLx_L \| x_R \leftarrow x_R + (x_L + k + c_i)^3 \| x_LxL​∥xR​←xR​+(xL​+k+ci​)3∥xL​，约束多项式被定义为：

1. xL(i+1)=xR(i)+(xL(i)+k+ci)3,x^{(i+1)}_L = x^{(i)}_R + (x^{(i)}_L + k + c_i)^3,xL(i+1)​=xR(i)​+(xL(i)​+k+ci​)3，
2. xR(i+1)=xL(i).x^{(i+1)}_R = x^{(i)}_L.xR(i+1)​=xL(i)​。

那么行数 t=324t = 324t=324，列数 w=2w = 2w=2，最大度数 d=3d = 3d=3。效率指标为 t⋅w⋅d=1944.t \cdot w \cdot d = 1944.t⋅w⋅d=1944。

实现

尽管作者建议使用 x3x^3x3 作为 S-box，但该 S-box 通常被替换为其他 S-box，如 x5,x7x^5, x^7x5,x7 如果 gcd⁡(3,q−1)=1\gcd(3, q-1) = 1gcd(3,q−1)=1。例如，BN254↗ 字段是 FqF_qFq​，对于 254 位素数 qqq，gcd⁡(3,q−1)≠1\gcd(3, q-1) \neq 1gcd(3,q−1)=1。因此，在 BN254 上使用 MiMC 时，最好使用 x5x^5x5 或 x7x^7x7，而不是 x3x^3x3 （ 示例 1↗，示例 2↗）。在这种情况下，轮数确定为 log⁡5q\log_5 qlog5​q 或 log⁡7q\log_7 qlog7​q，这减轻了目前为止提出的所有攻击。

对于轮常数，作者没有在论文中具体说明如何生成。因此，每个实现将通过计算类似 MiMC0 和 MiMC1 的字符串的哈希值来确定轮常数，使用 SHA-2↗ 或 SHA-3↗。如果某人创建了自己的 MiMC 实现，而没有披露如何生成轮常数，那么可能会存在潜在的漏洞，例如容易受到不变子场攻击。

Poseidon

Poseidon↗ 是另一个在 USENIX 2021 中提出的 ZK 友好的哈希函数。Poseidon 基于 HADES↗ 设计策略，这是对 置换-置换网络 (SPN)↗ 的概括，建议在 EUROCRYPT 2020 中使用。

HADES 设计策略

SPN 是一个著名的块密码算法。例如， AES↗ 使用 SPN 结构。通过足够交替回合的置换盒和置换盒，攻击者无法从明文-密文对中恢复密钥。

HADES 由三个步骤构成： 添加轮密钥、子字 和 混合层。

这似乎与 SPN 有相同的方法，但现有 SPN 与 HADES 的主要区别在于，HADES 中的部分 S-box 层是部分 S-box 层，这意味着单个 S-box 应用于最右边的元素，其他的保持不变。作者认为，这将降低 R1CS 或 AET 成本。

Poseidon 哈希函数

Poseidon 哈希函数的构造遵循 HADES，添加轮密钥 被替换为 添加轮常量。Poseidon 仅考虑素数域 Fp\mathbb F_pFp​。设 mmm 为每层中的字的数量（为避免与 STARK 中的行数 ttt 混淆，我们使用 mmm 而不是 ttt，代替论文中的符号）。下面是图形概览。

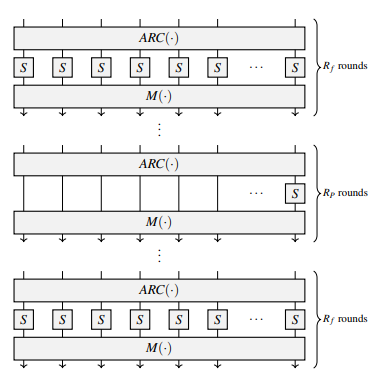Poseidon 的构造。RF=2⋅RfR_F = 2 \cdot R_fRF​=2⋅Rf​ 是完整 S-box 轮的数量，RPR_PRP​ 是部分 S-box 轮的数量。图片来自 Poseidon 论文。

S-box 定义为 S-box(x)=xα\text{S-box}(x) = x^\alphaS-box(x)=xα，其中 α≥3\alpha \geq 3α≥3 是满足 gcd⁡(α,p−1)=1\gcd(\alpha, p-1) = 1gcd(α,p−1)=1 的最小正整数。

线性层的目的是将局部变化传播到整个状态，因此通常选择线性层为 MDS 矩阵↗，其效果在成本上可以忽略不计。在 Poseidon 中，线性层是一个 Cauchy 矩阵↗，其定义为 M[i,j]=1xi+yjM[i,j] = \frac{1}{x_i + y_j}M[i,j]=xi​+yj​1​，其中 xix_ixi​ 和 yjy_jyj​ 彼此不同并且 xi+yj≠0x_i + y_j \neq 0xi​+yj​=0，且 i∈{1,…,m}i \in \{1, \dots, m\}i∈{1,…,m}，j∈{1,…,m}j \in \{1, \dots, m\}j∈{1,…,m}。这是 Poseidon 中的一个原创建议；然而，如果存在不变子空间路径，则某些 Cauchy 矩阵不安全。我们省略该攻击的细节。感兴趣的读者可以参考 论文↗。因此，线性层应仔细选择以避免这种类型的攻击。

该结构高度可参数化，且对于 256 位输出哈希的建议参数为 m=3,RF=8,RP=57m = 3, R_F = 8, R_P = 57，其中 α=5\alpha = 5α=5，且 ppp 约为 256 位。RF=8R_F = 8RF​=8 被选择以防止统计攻击，RP=57R_P = 57RP​=57 被选择以防止代数攻击。

SNARK 复杂度

对于 α=5\alpha = 5α=5，S-box xαx^\alphaxα 用三个约束表示：

x2 = x*x
x4 = x2*x2
x5 = x4*x

总 S-box 数量为 m⋅RF+RPm \cdot R_F + R_Pm⋅RF​+RP​。因此，对于 α=5\alpha = 5α=5，总约束数量为 3⋅(m⋅RF+RP)3 \cdot (m \cdot R_F + R_P)3⋅(m⋅RF​+RP​)。对于 m=3,RF=8,RP=57m = 3, R_F = 8, R_P = 57m=3,RF​=8,RP​=57，约需要 276276276 个 R1CS 约束。

STARK 复杂度

如果我们在每个轮中保持 mmm 个变量，则行数为 t=RF+RPt = R_F + R_Pt=RF​+RP​，列数为 w=kw = kw=k，最大度数为 d=αd = \alphad=α。然后效率指标为 t⋅w⋅d=(RF+RP)⋅m⋅αt \cdot w \cdot d = (R_F + R_P) \cdot m \cdot \alphat⋅w⋅d=(RF​+RP​)⋅m⋅α。然而，这种 AET 表示未能利用部分 S-box 轮。相反，通过将每个 S-box 输出视为变量，行数为 t=1t = 1t=1，列数为 w=m⋅RF+RPw = m \cdot R_F + R_Pw=m⋅RF​+RP​，而最大度数 ddd 仍为 α\alphaα。对于 m=3,RF=8,RP=57m = 3, R_F = 8, R_P = 57m=3,RF​=8,RP​=57，效率指标为 t⋅w⋅d=1⋅81⋅5=425t \cdot w \cdot d = 1 \cdot 81 \cdot 5 = 425t⋅w⋅d=1⋅81⋅5=425。

Vision / Rescue

Vision / Rescue↗ 是遵循卓越设计策略的 ZK 友好哈希函数。它们在 FSE 2020 中提出。

卓越设计策略

卓越设计是一种由元组 (q,m,π,M,v,s)(q, m, \pi, M, v, s)(q,m,π,M,v,s) 参数化的置换-置换网络：

• qqq : 字段为 Fq\mathbb F_qFq​，其中 qqq 要么是 222 的幂，要么是素数，
• mmm : 状态为 Fq\mathbb F_qFq​ 中的 mmm 个元素，
• π=(π0,π1)\pi = (\pi_0, \pi_1)π=(π0​,π1​) : S-box，
• MMM : 一个 MDS 矩阵↗，
• vvv : 第一步常数，
• sss : 所需的安全级别。在每一轮的 Marvelous 设计中，一对 S-box (π0, π1)(\pi_0, \pi_1)(π0​, π1​) 交替使用。π0\pi_0π0​ 和 π1\pi_1π1​ 之间的区别在于它们的度数。对于一个，π0\pi_0π0​ 在顺向评价时应该选择一个高的度数，而在逆向评价时选择一个低的度数。另一个 S-box，即 π1\pi_1π1​，则选择相反的目标，这意味着它在顺向方向上的度数较低，在逆向方向上的度数较高。这样的选择带来了三个好处：

1. 无论对手试图以哪个方向攻击，度数都保证是高的。
2. 加密和解密函数的成本相同。
3. 由于非程序性计算，每个 S-box 的低度表示可以高效地评估。

对于 Vision / Rescue，π0\pi_0π0​ 直接从 π1\pi_1π1​ 获得：π0=π1−1\pi_0 = \pi_1^{-1}π0​=π1−1​。

线性层通过 Vandermonde\ matrix↗ 选择。如同在 Poseidon 中所描述的，没有关于 Vandermonde 矩阵的安全声明，任何其它的 MDS 矩阵都应该没问题。

与其他算法的一个有趣区别是 Marvelous 使用了一个复杂的密钥调度。在 MiMC 和 HADES 中，没有特别的密钥调度，主密钥每轮都被添加。然而，在 Marvelous 中，密钥调度重用了轮函数。作者声称这是一个安全边际，因为 AOCs 的领域相对较新。需要注意的是，复杂的调度不影响固定密钥置换的哈希函数效率，因为每个子密钥都是在离线阶段派生的。

Vision

Vision 意在于其本地域 F_2n\mathbb F\_{2^n}F_2n 上操作。为了构造 S-box，我们选择度数 444，表示为 BBB。更准确地，我们在 B(x)B(x)B(x) 中没有 x3x^3x3 项：B(x)=b4⋅x4+b2⋅x2+b1⋅x1+b0B(x) = b_4 \cdot x^4 + b_2 \cdot x^2 + b_1 \cdot x^1 + b_0B(x)=b4​⋅x4+b2​⋅x2+b1​⋅x1+b0​。然后在 F2\mathbb F_2F2​ 上线性化 BBB，这对其他计算设置如 MPC↗ 有好处。然而，它与 SNARK/STARK 设置无关，因此我们不再进一步讨论。

选择 BBB 后，π0\pi_0π0​ 和 π1\pi_1π1​ 分别为：π0(x)=B−1(x−1)\pi_0(x) = B^{-1}(x^{-1})π0​(x)=B−1(x−1) 和 π1(x)=B(x−1)\pi_1(x) = B(x^{-1})π1​(x)=B(x−1)。

最后，为了应对最远攻击，轮数翻倍，这意味着增加 100% 的安全边际，轮数从 10 变为 16。

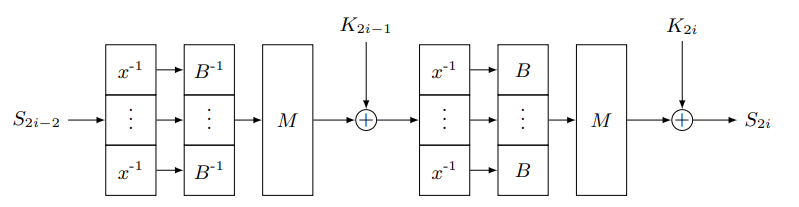Vision 的单轮（两步）。图片来自 Marvelous 论文。

Rescue

在 Marvelous 领域中的第二个算法家族是 Rescue。为了构建 S-box，应该找到最小的素数 α\alphaα，使得 gcd⁡(α,q−1)=1\gcd(\alpha, q-1) = 1gcd(α,q−1)=1。然后 S-box 被设置为 π0(x)=x1/α\pi_0(x) = x^{1/\alpha}π0​(x)=x1/α 和 π1(x)=xα\pi_1(x) = x^\alphaπ1​(x)=xα。轮数被翻倍以应对最远攻击，如同 Vision，并且轮数在 10 到 22 之间变化。

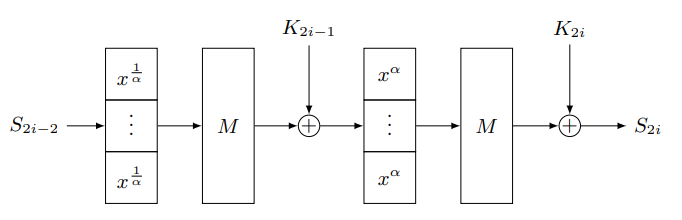Rescue 的单轮（两步）。图片来自 Marvelous 论文。

SNARK 复杂度

对于 Vision，我们应考虑反向映射 x−1x^{-1}x−1 和 B(x)B(x)B(x) — B−1(x)B^{-1}(x)B−1(x) 与 B(x)B(x)B(x) 类似。首先，对 x−1x^{-1}x−1，设 y=x−1y = x^{-1}y=x−1。如果 x=0x = 0x=0，则 y=0y = 0y=0；如果 x≠0x \neq 0x=0，则 xy=1xy = 1xy=1。将其结合，我们得到必要且充分条件 x(1+xy)=0x(1+xy) = 0x(1+xy)=0 和 y(1+xy)=0y(1+xy) = 0y(1+xy)=0。它由三个约束表示：

z = x*y
eq1 = x*(1+z)
eq2 = y*(1+z)

其次，对于 BBB，由于其度数为 444，它由两个约束表示：

x2 = x*x
x4 = x2*x2

注意，只有 x4x^4x4 和 x2x^2x2 被评估，而 B(x)=b4⋅x4+b2⋅x2+b1⋅x1+b0B(x) = b_4 \cdot x^4 + b_2 \cdot x^2 + b_1 \cdot x^1 + b_0B(x)=b4​⋅x4+b2​⋅x2+b1​⋅x1+b0​ 尚未推导。不过，这并不重要，因为 R1CS 的结构允许我们稍后乘以常量并加上变量。

单轮由两个步骤组成，每一步添加的约束为 3m+2m=5m3m + 2m = 5m3m+2m=5m。因此，总约束的数量为 10⋅m⋅r10 \cdot m \cdot r10⋅m⋅r，轮次为 rrr。从推荐参数 q≈2256,m=3,r=12q \approx 2^{256}, m = 3, r = 12q≈2256,m=3,r=12，约束的数量为 10×3×12=36010 \times 3 \times 12 = 36010×3×12=360。

对于 Rescue，只有 B(x)=xαB(x) = x^\alphaB(x)=xα 和 B(x)=x1/αB(x) = x^{1/\alpha}B(x)=x1/α 是非线性操作，对于 α=3\alpha = 3α=3，每个 B(x)B(x)B(x) 和 B−1(x)B^{-1}(x)B−1(x) 需要两个约束，正如我们在 MiMC 中看到的。因此，每一轮添加 4m4m4m 约束，总约束数量为 4⋅m⋅r4 \cdot m \cdot r4⋅m⋅r，对于轮距离 rrr。从推荐参数 q≈2256,m=3,r=22q \approx 2^{256}, m = 3, r = 22q≈2256,m=3,r=22，于是约束数量为 4×3×22=2644 \times 3 \times 22 = 2644×3×22=264。

STARK 复杂度

对于 Vision，作者提出一个 AIR，w=2m,t=2,d=2w = 2m, t = 2, d = 2w=2m,t=2,d=2，用于每一步。前 mmm 个元素对应于原始状态（如 S[i]S[i]S[i]），最后 mmm 个元素是存储的辅助值（如 R[i]R[i]R[i]）。在第一个周期中，R[i]=1R[i] = 1R[i]=1 当 S[i]=0S[i] = 0S[i]=0 时，其他情况下 R[i]=0R[i] = 0R[i]=0。我们将 S[i]S[i]S[i] 的值对应于下一行标记为 S′[i]S^\prime[i]S′[i]。我们的目标是使 S′[i]=S[i]−1S^\prime[i] = S[i]^{-1}S′[i]=S[i]−1。然后通过设置以下约束，验证 R[i]R[i]R[i] 和 S′[i]S^\prime[i]S′[i] 的值是正确的。

1. S[i]⋅S′[i]−R[i]=0,S[i] \cdot S^\prime[i] - R[i] = 0,S[i]⋅S′[i]−R[i]=0，
2. S[i]⋅(1−R[i])=0,S[i] \cdot (1 - R[i]) = 0,S[i]⋅(1−R[i])=0，
3. S′[i]⋅(1−R[i])=0.S^\prime[i] \cdot (1 - R[i]) = 0.S′[i]⋅(1−R[i])=0。

对于第二个周期，R[i]=S[i]2R[i] = S[i]^2R[i]=S[i]2。然后 S′[i]=B(S[i])S^\prime[i] = B(S[i])S′[i]=B(S[i])，R[i]R[i]R[i] 通过以下约束验证：

1. R[i]−S[i]2=0,R[i] - S[i]^2 = 0,R[i]−S[i]2=0，
2. S′[i]−b4⋅R[i]2−b2⋅R[i]−b1⋅S[i]−b0=0.S^\prime[i] - b_4 \cdot R[i]^2 - b_2 \cdot R[i] - b_1 \cdot S[i] - b_0 = 0.S′[i]−b4​⋅R[i]2−b2​⋅R[i]−b1​⋅S[i]−b0​=0。

当轮数为 rrr 时，w=2m,t=4r,d=2w = 2m, t = 4r, d = 2w=2m,t=4r,d=2。从推荐参数 q≈2256,m=3,r=12q \approx 2^{256}, m = 3, r = 12q≈2256,m=3,r=12，效率指标为 t⋅w⋅d=48⋅6⋅2=576t \cdot w \cdot d = 48 \cdot 6 \cdot 2 = 576t⋅w⋅d=48⋅6⋅2=576。

对于 Rescue，不需要辅助值。此外，可以将 B(x)B(x)B(x) 和 B−1(x)B^{-1}(x)B−1(x) 合并为一个方程。因此，对于 rrr 轮，w=m,t=r,d=3w = m, t = r, d = 3w=m,t=r,d=3。从推荐参数 q≈2256,m=3,r=22q \approx 2^{256}, m = 3, r = 22q≈2256,m=3,r=22，效率指标为 t⋅w⋅d=22⋅3⋅3=198t \cdot w \cdot d = 22 \cdot 3 \cdot 3 = 198t⋅w⋅d=22⋅3⋅3=198。

结论

在本文中，我们讨论了各种 AOC 的设计原理和性能。还有更多未提及的 AOC，如 GMiMC、Jarvis 和 Friday，但它们的设计原理与我们所涵盖的原则类似。

整体的 SNARK 和 STARK 性能如下所示。

如表格所示，Rescue 在 SNARK 和 STARK 中均具有竞争力的结果。事实上，STARKWARE 也在其自己的 调查↗ 中推荐了 Rescue 作为 STARK 友好的哈希函数。

近年来，提出了在 SNARK 设置下比 Rescue 效率提高 2-3 倍的哈希函数：Anemoi↗ 和 Griffin↗。它们尚未完全通过同行评审，需要通过学术界和业界的验证，但其卓越的性能意味着一旦成熟，便可考虑使用。

同时，AOC 的代数简单性往往允许攻击者攻击密码算法。因此，建议使用发布并历经时间验证可靠的密码算法，而不是仅仅基于效率来选择。在下一篇文章中，我们将讨论对 AOC 的代数攻击。

• 原文链接： zellic.io/blog/zk-friend...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～