以太坊签名方案解析：ECDSA、BLS、XMSS 以及带 Rust 代码示例的后量子 leanSig

本文深入探讨了以太坊中使用的几种签名方案，包括 ECDSA（用于交易签名）、BLS（用于共识聚合）和 XMSS（作为后量子候选方案），并讨论了每种方案的优缺点及其在以太坊未来发展中的作用，着重介绍了 Lean Ethereum 及其 leanSig/leanMultisig 如何通过结合哈希密码学和 SNARK 技术，实现可扩展且抗量子的共识层。

TL;DR: 以太坊中密码学签名的数学、代码、攻击和未来指南——从 ECDSA 交易到 BLS 共识聚合以及后量子精简签名。 包括使用 lambdaworks 的 Rust 代码示例。

2010 年，索尼 PlayStation 3 的安全性被认为是牢不可破的。 后来一位黑客注意到了一些奇怪的事情：索尼在签署其固件时两次使用了相同的随机数。 这个重复的数值让攻击者推导出索尼的主私钥。 每一台 PS3 都变得可以入侵。 我们能从中得到什么教训？ 数字签名的强度取决于其最薄弱的实现细节。

每次你在以太坊上发送交易时，你都是在提出一个只有你才能提出的数学主张，这是一种基于成熟难题的证明。 但问题是：我们正在基于量子计算机最终会破解的假设来构建关键基础设施。 那么前进的方向是什么？ 我们做好准备，这意味着了解我们实际依赖的是什么以及未来的样子。

本文考察了与以太坊当前和未来最相关的签名方案：用于交易签名的 ECDSA，用于共识聚合的 BLS，以及作为后量子候选者的 XMSS。 每一节都将数学定义与使用 lambdaworks 的 Rust 代码配对。 使用的 XMSS 版本不是以太坊的候选版本，但用于说明这一点。

签名方案的权衡概览

在我们深入研究之前，让我们承认一个令人不舒服的事实（这在工程领域几乎是普遍存在的）：没有完美的签名方案。 在速度、聚合能力、签名大小、后量子安全性和 SNARK 友好性之间存在权衡。

方案 签名大小 速度 量子安全 聚合 SNARK 友好
ECDSA 64 字节 ●●●●● ✗ ✗ (原生) ✗
BLS 48 字节 ●●●○○ ✗ ✓ (原生) ●●○○○
XMSS ~2,500 字节 ●●●○○ ✓ ✗ (原生) ●●●●○
leanSig 千字节（证明） ●●●○○ ✓ ✓ (通过 STARK) ●●●●●

BLS 为我们提供了原生聚合，但在后量子方面失败了。 XMSS 是量子安全的，但不能原生聚合。 leanSig 结合了两者的优点：量子抗性和基于 STARK 的聚合，尽管签名大小远大于 BLS。

第一部分：ECDSA — 以太坊交易的基础

椭圆曲线密码学如何工作

ECDSA 在有限域上的椭圆曲线上运行。 以太坊使用的曲线 (secp256k1) 定义为：

$y^2 = x^3 + 7 \pmod{p}$

其中 $p = 2^{256} - 2^{32} - 977$，这是一个经过精心选择的素数。

为什么选择这条特定的曲线？：

  1. $a = 0$ 简化了点加倍（减少了乘法运算）。
  2. $p$ 是伪梅森素数，使模约简更快。

这条曲线上的点在弦切律下形成一个群。 关键运算是标量乘法：给定一个点 $G$（生成器）和一个标量 $k$，计算 $kG = G + G + \cdots + G$（$k$ 次）。

椭圆曲线离散对数问题 (ECDLP) 指出：

给定点 $G$ 和 $Q = kG$，找到 $k$ 在计算上是不可行的。

对于 256 位曲线，最好的经典攻击（Pollard 的 rho）需要 $O(\sqrt{n}) \approx 2^{128}$ 次运算——远远超出当前的计算能力。

使用 lambdaworks 进行有限域算术

在使用椭圆曲线之前，我们需要有限域算术。 以下是 lambdaworks 如何处理此问题，使用库中已内置的 secp256k1 字段定义：

use lambdaworks_math::elliptic_curve::short_weierstrass::curves::secp256k1::curve::Secp256k1FieldElement;
use lambdaworks_math::field::element::FieldElement;

// Field elements in F_p where p = 2^256 - 2^32 - 977
// F_p 中的域元素，其中 p = 2^256 - 2^32 - 977
let a = Secp256k1FieldElement::from(7u64);
let b = Secp256k1FieldElement::from(11u64);

// All arithmetic is automatically mod p
// 所有算术运算都会自动对 p 取模
let sum = &a + &b;          // (7 + 11) mod p = 18
let product = &a * &b;      // (7 × 11) mod p = 77
let inverse = a.inv().unwrap(); // 7^(-1) mod p
assert_eq!(&a * &inverse, Secp256k1FieldElement::one());

这是所有后续操作的基础。 每一个点加法、每一个标量乘法、每一个签名计算都发生在这个域中。

lambdaworks 示例参考： Pohlig-Hellman 示例演示了对弱群的离散对数攻击，展示了实践中的有域算术。

ECDSA 密钥生成

密钥生成算法非常简单：

ECDSA-KeyGen():
    1. Select random d ∈ [1, n-1]        // Private key (256-bit integer)
    // 1. 选择随机 d ∈ [1, n-1] // 私钥（256 位整数）
    2. Compute Q = d × G                  // Public key (curve point)
    // 2. 计算 Q = d × G // 公钥（曲线点）
    3. Return (d, Q)
    // 3. 返回 (d, Q)

在 Rust 中，使用来自 lambdaworks 的椭圆曲线类型：

use lambdaworks_math::elliptic_curve::short_weierstrass::curves::secp256k1::curve::Secp256k1;
use lambdaworks_math::elliptic_curve::traits::IsEllipticCurve;
use lambdaworks_math::unsigned_integer::element::UnsignedInteger;

// The generator point G for secp256k1 is built into lambdaworks
// secp256k1 的生成器点 G 内置于 lambdaworks 中
let generator = Secp256k1::generator();

// Private key: a random 256-bit scalar
// 私钥：一个随机的 256 位标量
// In production, use a cryptographically secure RNG
// 在生产环境中，使用加密安全 RNG
let private_key = UnsignedInteger::<4>::from_hex_unchecked(
    "c6b506142fb077e8f06e8e1b2b12a8c63ed60abe2bdb4fea50e39e12ef9e5298"
);

// Public key: Q = d × G (scalar multiplication)
// 公钥：Q = d × G （标量乘法）
let public_key = generator.operate_with_self(private_key);
// This point (x, y) is your Ethereum address (after hashing)
// 这个点 (x, y) 是你的以太坊地址（哈希后）

ECDSA 签名算法

签名算法揭示了 ECDSA 的危险代数：

ECDSA-Sign(d, message):
    1. e = H(message)                     // Hash the message (256 bits)
    // 1. e = H(message)                     // 哈希消息（256 位）
    2. Select random k ∈ [1, n-1]         // THE NONCE - this is critical!
    // 2. 选择随机 k ∈ [1, n-1]         // 随机数 - 这至关重要！
    3. Compute R = k × G                  // Ephemeral point
    // 3. 计算 R = k × G // 临时点
    4. r = R.x mod n                      // x-coordinate becomes r
    // 4. r = R.x mod n // x 坐标变为 r
    5. s = k⁻¹(e + r·d) mod n            // THE SIGNATURE EQUATION
    // 5. s = k⁻¹(e + r·d) mod n // 签名方程
    6. Return (r, s)
    // 6. 返回 (r, s)

签名方程是我们组合所有相关数据的地方：

$s = k^{-1}(e + r \cdot d) \pmod{n}$

这个方程将以下内容联系在一起：

  • $e$：消息哈希（签名后公开）
  • $r$：从 $kG$ 导出（在签名中公开）
  • $d$：你的私钥（秘密！）
  • $k$：随机数（必须保持秘密且唯一）

以下是使用 lambdaworks 逐步实现的完整签名算法。 我们直接使用 secp256k1 曲线类型和标量域算术，并镜像伪代码的每一行：

use lambdaworks_math::elliptic_curve::short_weierstrass::curves::secp256k1::curve::Secp256k1;
use lambdaworks_math::elliptic_curve::short_weierstrass::curves::secp256k1::field_extension::Secp256k1PrimeField;
use lambdaworks_math::elliptic_curve::traits::IsEllipticCurve;
use lambdaworks_math::field::element::FieldElement;
use lambdaworks_math::cyclic_group::IsGroup;

type ScalarField = FieldElement<Secp256k1PrimeField>;

/// ECDSA signing using lambdaworks primitives.
/// 使用 lambdaworks 基本体的 ECDSA 签名。
/// Returns (r, s) as scalar field elements.
/// 以标量域元素形式返回 (r, s)。
fn ecdsa_sign(
    private_key: &ScalarField,  // d
    msg_hash: &ScalarField,     // e = H(message)
    msg_hash: &ScalarField,     // e = H(消息)
    nonce: &ScalarField,        // k — in production, derive via RFC 6979!
    nonce: &ScalarField,        // k — 在生产中，通过 RFC 6979 派生！
) -> (ScalarField, ScalarField) {
    let generator = Secp256k1::generator();

    // Step 1: R = k × G (ephemeral point on the curve)
    // 步骤 1：R = k × G （曲线上的临时点）
    let r_point = generator.operate_with_self(nonce.canonical());

    // Step 2: r = R.x mod n (extract x-coordinate as a scalar)
    // 步骤 2：r = R.x mod n （提取 x 坐标作为标量）
    let [x, _y] = r_point.to_affine().coordinates();
    let r = ScalarField::new(x.canonical());

    // Step 3: s = k⁻¹ · (e + r·d) mod n  — THE SIGNATURE EQUATION
    // 步骤 3：s = k⁻¹ · (e + r·d) mod n — 签名方程
    let k_inv = nonce.inv().unwrap();
    let s = &k_inv * &(msg_hash + &(&r * private_key));

    (r, s)
}

ECDSA 验证：为什么它有效

ECDSA-Verify(Q, message, (r, s)):
    1. e = H(message)
    2. u₁ = e · s⁻¹ mod n
    3. u₂ = r · s⁻¹ mod n
    4. R' = u₁ × G + u₂ × Q
    5. Return (R'.x mod n == r)

验证，再次逐步进行：

/// ECDSA verification using lambdaworks primitives.
/// 使用 lambdaworks 基本体的 ECDSA 验证。
/// Q is the public key (a curve point), (r, s) is the signature.
/// Q 是公钥（一个曲线点），(r, s) 是签名。
fn ecdsa_verify(
    public_key: &ShortWeierstrassProjectivePoint<Secp256k1>,
    msg_hash: &ScalarField,     // e = H(message)
    msg_hash: &ScalarField,     // e = H(消息)
    r: &ScalarField,
    s: &ScalarField,
) -> bool {
    let generator = Secp256k1::generator();

    // Step 1: s_inv = s⁻¹ mod n
    // 步骤 1：s_inv = s⁻¹ mod n
    let s_inv = s.inv().unwrap();

    // Step 2: u₁ = e · s⁻¹,  u₂ = r · s⁻¹
    // 步骤 2：u₁ = e · s⁻¹, u₂ = r · s⁻¹
    let u1 = msg_hash * &s_inv;
    let u2 = r * &s_inv;

    // Step 3: R' = u₁·G + u₂·Q  (two scalar multiplications + point addition)
    // 步骤 3：R' = u₁·G + u₂·Q (两个标量乘法 + 点加法)
    let r_prime = generator
        .operate_with_self(u1.canonical())
        .operate_with(&public_key.operate_with_self(u2.canonical()));

    // Step 4: Check R'.x mod n == r
    // 步骤 4：检查 R'.x mod n == r
    let [x_prime, _] = r_prime.to_affine().coordinates();
    ScalarField::new(x_prime.canonical()) == *r
}

请注意，每一行代码都直接映射到伪代码的一行。 基础域算术——模逆、乘法和椭圆曲线标量乘法——由 lambdaworks 处理。

正确性证明： 从验证计算开始：

$R' = u_1G + u_2Q$

替换 $Q = dG$：

$R' = u_1G + u_2(dG) = (u_1 + u_2d)G$

现在替换 $u_1 = es^{-1}$ 和 $u_2 = rs^{-1}$：

$R' = s^{-1}(e + rd)G$

从签名中回忆一下 $s = k^{-1}(e + rd)$，这意味着 $(e + rd) = sk$：

$R' = s^{-1}(sk)G = kG = R$

验证重建了原始点 $R$！ 由于 $r = R.x \pmod{n}$，因此签名通过验证。 关键的见解是，验证本质上是“撤消”签名期间执行的掩码。 值 $s$ 以一种需要知道 $d$ 才能计算的方式编码 $k$，但验证仅使用公共信息重建 $kG$。

lambdaworks 示例参考： Naive Schnorr 签名示例演示了一种结构相似的密切相关的签名方案。 Schnorr 签名使用一个更简单的方程 ($s = k - e \cdot d$)。

随机数灾难：为什么 k 永远不能重复使用

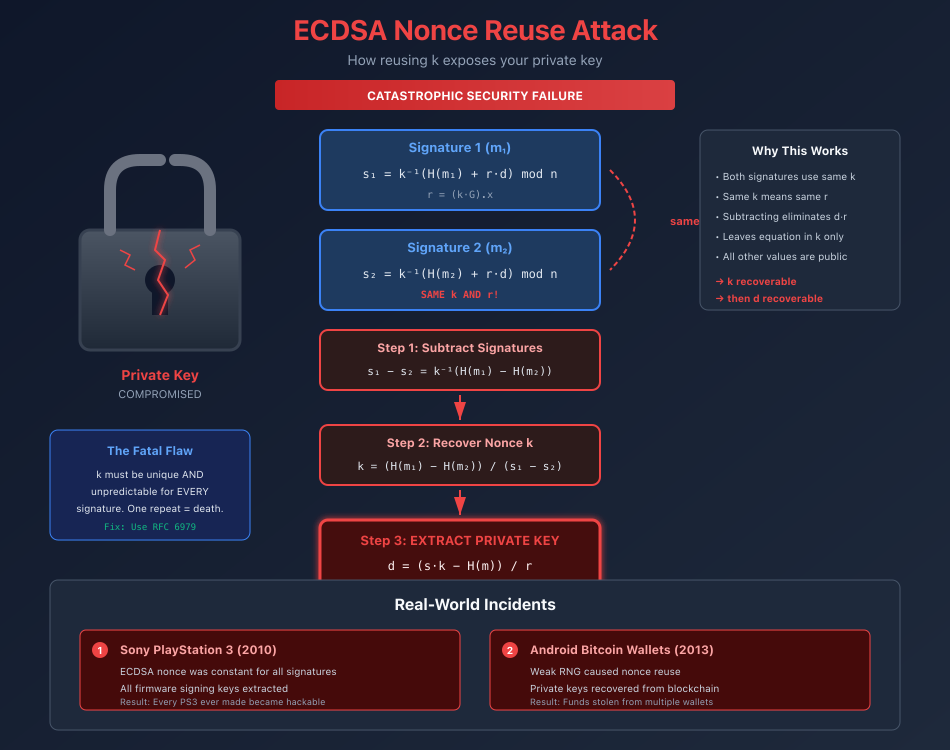
01-ecdsa-nonce-reuse-attack

现在我们到达了 ECDSA 最危险的部分。 随机数 $k$ 就像一次性密码本，只是重复使用的后果以不同的方式是灾难性的。 重复使用一次性密码本，你的消息就会变得可读。 重复使用 ECDSA 随机数，你的私钥就变得可计算（因此任何人都可以伪造签名）。

完整的攻击推导：

假设攻击者观察到对不同消息 $m_1$ 和 $m_2$ 的两个签名，这两个签名都使用相同的随机数 $k$ 签名：

$s_1 = k^{-1}(e_1 + r \cdot d) \pmod{n}$ $s_2 = k^{-1}(e_2 + r \cdot d) \pmod{n}$

注意：相同的 $k$ 意味着相同的 $r$（因为 $r = (kG).x$）。 攻击者注意到 $r_1 = r_2$。

第一步：减去方程

$s_1 - s_2 = k^{-1}(e_1 - e_2) \pmod{n}$

第二步：求解 $k$

$k = \frac{e_1 - e_2}{s_1 - s_2} \pmod{n}$

右侧的一切都是公开的！ 攻击者现在知道 $k$。

第三步：提取私钥

$d = \frac{s \cdot k - e}{r} \pmod{n}$

游戏结束： 私钥从公开可观察到的数据中恢复。

工作示例：使用小数字的随机数复用攻击

让我们通过一个具体的例子来分析:

设置：

  • $n = 23$ (群阶)
  • 私钥: $d = 7$
  • 随机数 (复用!): $k = 5$
  • 假设 $r = (kG).x \pmod{23} = 15$

第一个签名 在消息上，其中 $e_1 = H(m_1) = 11$:

$s_1 = k^{-1}(e_1 + rd) = 5^{-1}(11 + 15 \times 7) \pmod{23}$

我们需要 $5^{-1} \pmod{23}$。 因为 $5 \times 14 = 70 = 3 \times 23 + 1$，所以 $5^{-1} = 14$。

$s_1 = 14 \times (11 + 105) = 14 \times 116 = 14 \times (116 \pmod{23}) = 14 \times 1 = 14$

第二个签名 在消息上，其中 $e_2 = H(m_2) = 3$:

$s_2 = 14 \times (3 + 105) = 14 \times 108 = 14 \times (108 \pmod{23}) = 14 \times 16 = 224 \pmod{23} = 17$

攻击：

$k = \frac{e_1 - e_2}{s_1 - s_2} = \frac{11 - 3}{14 - 17} = \frac{8}{-3} \pmod{23}$

因为 $-3 \equiv 20 \pmod{23}$ 且 $20^{-1} = 15$（因为 $20 \times 15 = 300 = 13 \times 23 + 1$）：

$k = 8 \times 15 = 120 \pmod{23} = 5 \checkmark$

现在提取 $d$：

$d = \frac{s_1 \cdot k - e_1}{r} = \frac{14 \times 5 - 11}{15} = \frac{59}{15} \pmod{23}$

$59 \pmod{23} = 13$，且 $15^{-1} = 20$：

$d = 13 \times 20 = 260 \pmod{23} = 7 \checkmark$

私钥 $d = 7$ 被恢复。 这是使用 lambdaworks 域算术对此攻击的 Rust 模拟：

use lambdaworks_math::field::element::FieldElement;
use lambdaworks_math::field::fields::u64_prime_field::U64PrimeField;

// Working in Z_23 (small field for demonstration)
// 在 Z_23 中工作（小规模，用于演示）
type F = U64PrimeField<23>;
type FE = FieldElement<F>;

fn nonce_reuse_attack() {
    let d = FE::from(7u64);  // Secret key (attacker doesn't know this)
    // 秘密密钥（攻击者不知道这个）
    let k = FE::from(5u64);  // Nonce (reused!)
    // 随机数（已复用！）
    let r = FE::from(15u64); // From kG.x
    // 来自 kG.x

    // Two signatures with the SAME nonce
    // 两个使用相同随机数的签名
    let e1 = FE::from(11u64);
    let s1 = k.inv().unwrap() * (&e1 + &r * &d); // s1 = 14

    let e2 = FE::from(3u64);
    let s2 = k.inv().unwrap() * (&e2 + &r * &d); // s2 = 17

    // === THE ATTACK (uses only public data) ===
    // === 攻击（仅使用公共数据） ===
    // Step 1: Recover k
    // 步骤 1：恢复 k
    let k_recovered = (&e1 - &e2) * (&s1 - &s2).inv().unwrap();
    assert_eq!(k_recovered, FE::from(5u64)); // k = 5 ✓

    // Step 2: Recover private key
    // 步骤 2：恢复私钥
    let d_recovered = (&s1 * &k_recovered - &e1) * r.inv().unwrap();
    assert_eq!(d_recovered, FE::from(7u64)); // d = 7 ✓

    println!("Private key recovered: d = 7");
    // 打印 “私钥已恢复：d = 7”
}

现实世界中的 ECDSA 随机数灾难

这不仅仅是学术知识。 以下是人们犯错时发生的事情：

事件 年份 哪里出错了 影响
Sony PS3 2010 恒定的随机数 提取了所有固件签名密钥
Android Bitcoin 2013 弱 RNG 生成重复的随机数 从钱包中窃取比特币
IOTA 2017 自定义哈希函数存在弱点 Curl 哈希冲突启用了伪造

解决方案：RFC 6979

现代实现确定性地派生 $k$：

$k = \text{HMAC-DRBG}(\text{private_key}, \text{message_hash})$

这是确定性的（相同的输入 → 相同的 $k$），唯一的（不同的消息 → 不同的 $k$），并且是秘密的（取决于私钥）。

第二部分：BLS 签名 — 以太坊如何扩展到 100 万验证者

在这一点上，一个合理的问题是：“为什么不在所有地方都使用 ECDSA？” 当你尝试扩展时，答案会变得很清楚。

以太坊有超过 900,000 个验证者。 每个Slot都需要来自数千个验证者的证明。 使用 ECDSA，这意味着每 12 秒验证数千个单独的签名。 BLS 签名聚合完全改变了数学运算。

双线性配对：聚合背后的数学

BLS 依赖于双线性配对，这是一种数学运算，看起来应该打破一切（它最初用于尝试破解离散对数问题），但相反，它可以实现高效聚合。

定义： 双线性配对是一个映射：

$e: G_1 \times G_2 \rightarrow G_T$

满足双线性属性：

$e(aP, bQ) = e(P, Q)^{ab}$

这让我们可以在“指数中相乘”，在加法群（$G_1$，$G_2$）和乘法群（$G_T$）之间移动。

BLS 签名方案

BLS 签名的算法是（你可以交换哪个群持有公钥 vs 签名）：

密钥生成：

sk ← random scalar in Z_p
pk = sk × G₂ ∈ G₂

签名：

H = hash_to_curve(message) ∈ G₁
σ = sk × H ∈ G₁

验证：

Check: e(σ, G₂) = e(H(m), pk)

为什么 BLS 验证有效

从左侧开始：

$e(\sigma, G_2) = e(sk \cdot H(m), G_2) = e(H(m), G_2)^{sk}$

现在是右侧：

$e(H(m), pk) = e(H(m), sk \cdot G_2) = e(H(m), G_2)^{sk}$

两侧都等于 $e(H(m), G_2)^{sk}$。 配对的双线性属性使我们可以在两个参数之间移动标量因子——这是使 BLS 工作的数学魔力。

使用 lambdaworks 对 BLS 进行签名和验证

我们可以直接使用 lambdaworks 的 BLS12-381 曲线和配对支持来实现 BLS 签名和验证。 签名只是 $G_1$ 中的标量乘法； 验证是配对检查：

use lambdaworks_math::elliptic_curve::short_weierstrass::curves::bls12_381::{
    curve::BLS12381Curve,
    twist::BLS12381TwistCurve,
    pairing::BLS12381AtePairing,
    field_extension::BLS12381PrimeField,
};
use lambdaworks_math::elliptic_curve::traits::{IsEllipticCurve, IsPairing};
use lambdaworks_math::cyclic_group::IsGroup;
use lambdaworks_math::field::element::FieldElement;

type ScalarField = FieldElement<BLS12381PrimeField>;

/// BLS key generation: sk is a random scalar, pk = sk × G₂
/// BLS 密钥生成：sk 是一个随机标量，pk = sk × G₂
fn bls_keygen(sk: u64) -> (u64, /* pk */ impl IsGroup) {
    let g2 = BLS12381TwistCurve::generator();
    let pk = g2.operate_with_self(sk);
    (sk, pk)
}

/// BLS signing: σ = sk × H(m)
/// BLS 签名：σ = sk × H(m)
/// Here we simplify hash-to-curve as scalar × G₁ for illustration.
/// 在这里，我们为了便于说明，将哈希到曲线简化为标量 × G₁。
/// A production implementation MUST use a proper hash_to_curve (RFC 9380).
/// 生产环境的实现必须使用正确的 hash_to_curve（RFC 9380）。
fn bls_sign(sk: u64, msg_point: &impl IsGroup) -> impl IsGroup {
    msg_point.operate_with_self(sk)
}

/// BLS verification: check e(σ, G₂) == e(H(m), pk)
/// BLS 验证：检查 e(σ, G₂) == e(H(m), pk)
fn bls_verify(
    signature: &ShortWeierstrassProjectivePoint<BLS12381Curve>,
    msg_point: &ShortWeierstrassProjectivePoint<BLS12381Curve>,
    public_key: &ShortWeierstrassProjectivePoint<BLS12381TwistCurve>,
) -> bool {
    let g2 = BLS12381TwistCurve::generator();

    // Left side:  e(σ, G₂)
    // 左侧：e(σ, G₂)
    let lhs = BLS12381AtePairing::compute(signature, &g2);
    // Right side: e(H(m), pk)
    // 右侧：e(H(m), pk)
    let rhs = BLS12381AtePairing::compute(msg_point, public_key);

    lhs == rhs  // Bilinearity guarantees equality for valid signatures
    // 双线性性保证了有效签名的相等性
}

关于哈希到曲线的说明： 上面的代码段将 H(m) 简化为 $G_1$ 的标量倍数。 真正的 BLS 实现必须使用符合标准的哈希到曲线函数（RFC 9380）来将任意消息映射到 $G_1$ 上的点，而不会引入任何可利用的结构。 lambdaworks 提供了 BLS12-381 曲线基础设施，在此基础上可以构建此类函数。

BLS 签名聚合：以太坊扩展的关键

如果没有聚合，我们需要保留所有验证者的所有签名，并分别验证它们。 这会随着验证者的数量线性扩展，并成为扩展的严重问题。 例如，如果 16384 个验证者必须签名，我们需要 $16384 \times 64 \text{bytes} = 2^{20} \text{bytes} = 1 \text{MB}$。 通过聚合，即使聚合签名的验证时间比单个 EDCSA 慢，但它比对 $N$ 足够大进行线性工作更有效（在存储和验证方面）。 特别是，使用 BLS 聚合，聚合签名的大小为 48 字节，与单个签名的大小完全相同。

给定 $n$ 个对同一消息的签名 $\sigma_1, \dots, \sigma_n$：

$\sigma_{agg} = \sigma_1 + \sigma_2 + \cdots + \sigma_n$

聚合形式仍然压缩为 48 字节。 验证：

$e(\sigma_{agg}, G_2) \stackrel{?}{=} e(H(m), pk_1 + pk_2 + \cdots + pk_n)$

证明这是有效的：

$e(\sigma_{agg}, G2) = e(\sum{i=1}^{n} sk_i \cdot H(m), G2) = \prod{i=1}^{n} e(H(m), G_2)^{sk_i} = e(H(m), G_2)^{\sum sk_i} = e(H(m), \sum pk_i)$

带宽节省：

验证者 没有聚合 具有聚合 节省
100 4.8 KB 48 字节 99%
1,000 48 KB 48 字节 99.9%
100,000 4.8 MB 48 字节 99.999%

如果没有 BLS，以太坊当前的验证者集合是不可能的。 当然，我们仍然需要跟踪谁签署了消息，但那是一个位字符串，与集合中验证者的数量一样长。

代码中的聚合很简单——它只是 $G_1$ 中的点加法：

/// Aggregate n BLS signatures into one.
/// 将 n 个 BLS 签名聚合为一个。
/// sig_agg = σ₁ + σ₂ + ... + σₙ  (point addition in G₁)
/// sig_agg = σ₁ + σ₂ + ... + σₙ (G₁ 中的点加法)
fn bls_aggregate(
    signatures: &[ShortWeierstrassProjectivePoint<BLS12381Curve>],
) -> ShortWeierstrassProjectivePoint<BLS12381Curve> {
    signatures
        .iter()
        .skip(1)
        .fold(signatures[0].clone(), |acc, sig| acc.operate_with(sig))
}

/// Aggregate n public keys for same-message verification.
/// 聚合 n 个公钥以进行相同消息验证。
/// pk_agg = pk₁ + pk₂ + ... + pkₙ  (point addition in G₂)
/// pk_agg = pk₁ + pk₂ + ... + pkₙ (G₂ 中的点加法)
fn bls_aggregate_public_keys(
    public_keys: &[ShortWeierstrassProjectivePoint<BLS12381TwistCurve>],
) -> ShortWeierstrassProjectivePoint<BLS12381TwistCurve> {
    public_keys
        .iter()
        .skip(1)
        .fold(public_keys[0].clone(), |acc, pk| acc.operate_with(pk))
}

// Usage: verify the aggregate with a SINGLE pairing check
// 用法：使用单个配对检查验证聚合
// e(sig_agg, G₂) == e(H(m), pk_agg)
let is_valid = bls_verify(&sig_agg, &msg_point, &pk_agg);

无论 100 个还是 1,000,000 个验证者签名，验证成本都是单个配对检查。

代码中的基于配对的验证

在 lambdaworks 中使用 BLS12-381 配对：

use lambdaworks_math::elliptic_curve::short_weierstrass::curves::bls12_381::curve::BLS12381Curve;
use lambdaworks_math::elliptic_curve::short_weierstrass::curves::bls12_381::twist::BLS12381TwistCurve;
use lambdaworks_math::elliptic_curve::short_weierstrass::curves::bls12_381::pairing::BLS12381AtePairing> **注意:** lambdaworks 提供了完整的 [BLS12-381 配对实现](https://github.com/lambdaclass/lambdaworks/tree/main/math/src/elliptic_curve/short_weierstrass/curves/bls12_381)，包括最佳的 ate 配对和 Miller 循环——与以太坊共识层使用的相同操作。

### BLS 上的恶意密钥攻击

BLS 有一些几乎令人怀疑的地方。这种"受控泄漏"实现了聚合，但如果我们不小心，它也会导致攻击。

**攻击场景：**

1. Alice 拥有公钥 $pk_A = sk_A \cdot G_2$
2. Mallory 观察到 $pk_A$ 并创建一个**恶意公钥**：

$pk_M^{rogue} = sk_M \cdot G_2 - pk_A = (sk_M - sk_A) \cdot G_2$
3. Mallory 注册 $pk_M^{rogue}$ 作为她的公钥
4. 现在看看聚合后的公钥：

$pk_A + pk_M^{rogue} = pk_A + sk_M \cdot G_2 - pk_A = sk_M \cdot G_2$

**Alice 的密钥消失了！**
5. Mallory 单独签署一条消息：$\sigma = sk_M \cdot H(m)$
6. 这验证为来自 Alice 和 Mallory 的联合签名!

**防御：所有权证明 (PoP)**

每个参与者必须通过签署他们自己的公钥来证明他们知道他们的私钥：

$\pi = sk \cdot H_{pop}(pk)$

Mallory 无法为她的恶意密钥创建有效的 PoP，因为她不知道 $pk_M^{rogue} = (sk_M - sk_A) \cdot G_2$ 的离散对数。她知道 $sk_M$，但不知道 $sk_A$。以太坊要求在验证者注册期间提供 PoP。

* * *

## 第三部分：XMSS - 用于量子安全的基于哈希的签名

BLS 为我们提供了聚合，但它与 ECDSA 有着相同的弱点：两者都会受到量子攻击的影响。Shor 算法在多项式时间内解决离散对数问题，复杂度为 $O(n^3)$ 而不是 $O(2^{n/2})$。

如果你相信大规模量子计算机即将到来，那么我们需要基于不同硬度假设的方案。基于哈希的签名就是答案。它们的安全性可以归结为一个非常清晰的陈述：**如果哈希函数是安全的，那么签名也是安全的。**

### 以太坊面临的量子威胁

| 方案 | 经典攻击 | 量子攻击 (Shor) | 量子攻击 (Grover) |
| --- | --- | --- | --- |
| ECDSA-256 | $2^{128}$ | **多项式** ❌ | 不适用 |
| BLS12-381 | $2^{128}$ | **多项式** ❌ | 不适用 |
| XMSS-256 | $2^{256}$ | 不适用 | $2^{128}$ ✓ |

**为什么 XMSS 能够存活：** Shor 算法无法利用任何代数结构。安全性仅取决于哈希函数的属性。Grover 只提供了二次加速：$2^n \rightarrow 2^{n/2}$。

### WOTS+：一次性构建块

XMSS 基于 Winternitz 一次性签名 (WOTS+) 构建，该方案中每个密钥只能签署一条消息。

**哈希链构造：**

位置: 0 1 2 3 ... w-1 | | | | | sk → H(sk) → H²(sk) → H³(sk) → ... → pk ↑ ↑ 密钥 公钥


对于 Winternitz 参数 $w = 16$：每个链有 16 个位置（0 到 15），消息数字是 16 进制的（每个 4 位），并且 256 位的哈希产生 64 个消息链 + 3 个校验和链 = 总共 67 个。

要签署消息数字 $d$，请显示相应链中的位置 $d$。验证者始终可以向前哈希以检查签名：

消息哈希数字：[7, 10, 3, 15, 2, ...]

链 0：显示位置 7 → 验证者哈希 8 次以到达 pk 链 1：显示位置 10 → 验证者哈希 5 次以到达 pk 链 2：显示位置 3 → 验证者哈希 12 次以到达 pk


### 使用 lambdaworks 构建哈希链

哈希链是 XMSS 的核心原语。以下是如何使用 lambdaworks 构建一个：

```rust
use lambdaworks_crypto::hash::sha3::Sha3Hasher;
use lambdaworks_crypto::hash::traits::IsCryptoHash;

/// 从密钥构建长度为 `steps` 的 WOTS+ 哈希链
fn hash_chain(secret: &[u8; 32], steps: usize) -> Vec<[u8; 32]> {
    let hasher = Sha3Hasher::new();
    let mut chain = Vec::with_capacity(steps + 1);
    chain.push(*secret);

    for i in 0..steps {
        let prev = &chain[i];
        // 向前哈希: H(H(...H(sk)...))
        let hash_output = hasher.hash(prev);
        let mut next = [0u8; 32];
        next.copy_from_slice(&hash_output[..32]);
        chain.push(next);
    }
    chain
}

// 公钥是链的结尾
// 密钥是开始
let secret = [0x42u8; 32];
let chain = hash_chain(&secret, 15); // w=16, 位置 0..15
let public_key = chain[15]; // 已发布
let signing_key = chain[0]; // 密钥!

// 要签署数字 d=7：显示 chain[7]
// 验证者哈希 8 次：H^8(chain[7]) 应该等于 public_key
let mut verification = chain[7];
let hasher = Sha3Hasher::new();
for _ in 0..8 {
    let h = hasher.hash(&verification);
    verification.copy_from_slice(&h[..32]);
}
assert_eq!(verification, public_key); // 签名有效!

lambdaworks 示例参考： Merkle Tree CLI 示例演示了如何使用 lambdaworks 的加密原语构建 Merkle 树。XMSS 使用 WOTS+ 公钥的 Merkle 树——相同的构造，应用于签名密钥管理。

XMSS 密钥重用攻击

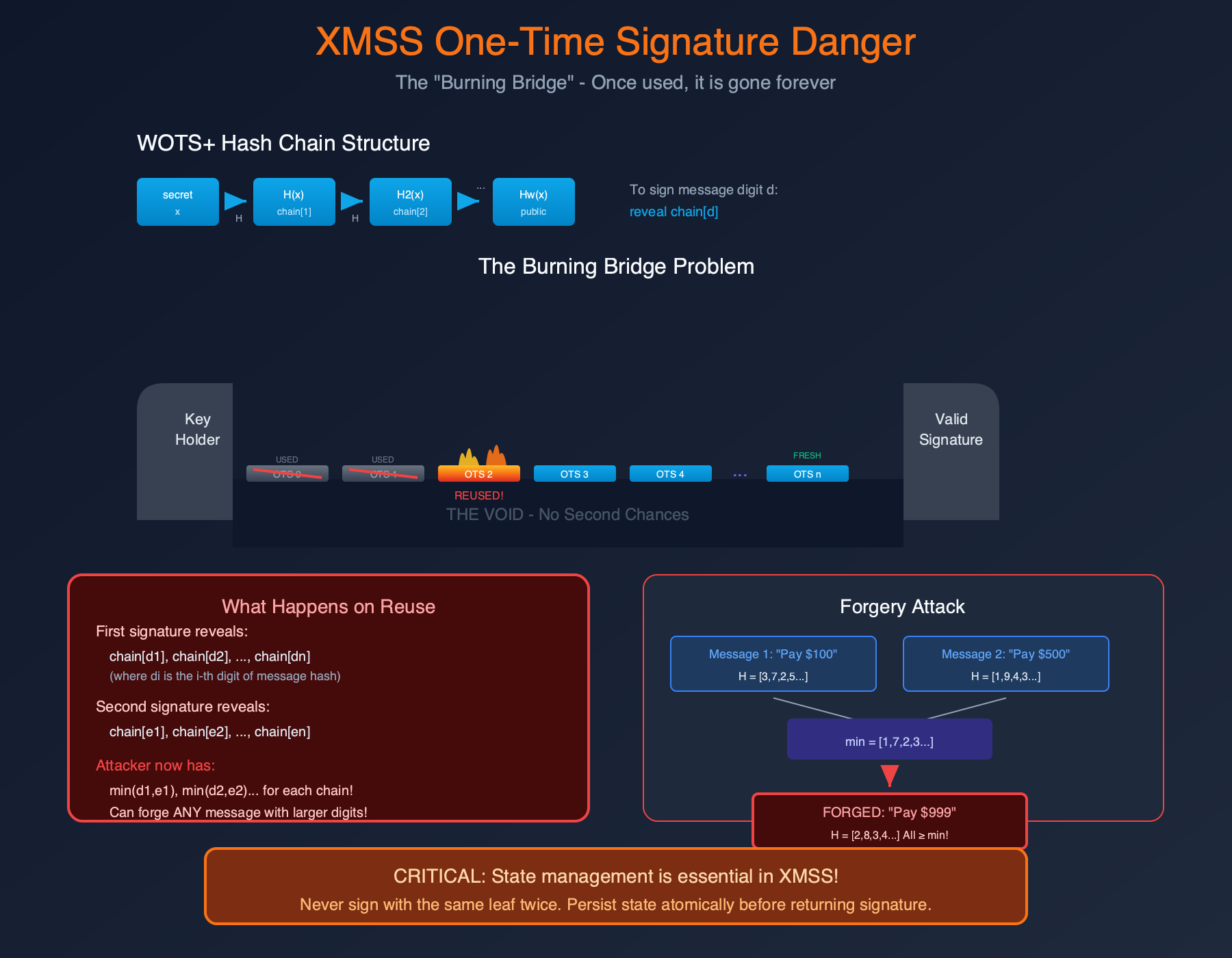
03-xmss-one-time-danger

XMSS 与 ECDSA 和 BLS 的根本区别在于：使用相同的临时密钥签名两次是灾难性的。

设置： 相同的 WOTS+ 密钥签名两条消息：

  • 消息 1：数字 $M_1 = [7, 10, 3, 15, 2, 8, \dots]$
  • 消息 2：数字 $M_2 = [4, 12, 9, 6, 11, 8, \dots]$
链 来自 $M_1$ 来自 $M_2$ 攻击者知道
0 位置 7 位置 4 位置 4–15
1 位置 10 位置 12 位置 10–15
2 位置 3 位置 9 位置 3–15
3 位置 15 位置 6 位置 6–15
4 位置 2 位置 11 位置 2–15
5 位置 8 位置 8 位置 8–15

关键的见解是，对于每个链，攻击者可以计算任何 ≥ min($M_1[i]$, $M_2[i]$) 的位置。攻击者可以伪造任何消息 $M_3$ 上的签名，其中 $\forall i: M_3[i] \ge \min(M_1[i], M_2[i])$。这是一个巨大的可伪造消息空间。

使用 $w = 4$ 的工作示例：

消息 1: M₁ = [2, 1, 3, 0]
消息 2: M₂ = [1, 3, 0, 2]

攻击者每个链的能力:
  链 0: min(2,1) = 1 → 可以伪造数字 1, 2, 3
  链 1: min(1,3) = 1 → 可以伪造数字 1, 2, 3
  链 2: min(3,0) = 0 → 可以伪造数字 0, 1, 2, 3 (有密钥!)
  链 3: min(0,2) = 0 → 可以伪造数字 0, 1, 2, 3 (有密钥!)

目标: M₃ = [2, 2, 1, 1] — 这是可伪造的吗?
  链 0: 需要 2, 有 1 → 计算 H(sig₂[0]) ✓
  链 1: 需要 2, 有 1 → 计算 H(sig₁[1]) ✓
  链 2: 需要 1, 有 0 → 计算 H(sig₂[2]) ✓
  链 3: 需要 1, 有 0 → 计算 H(sig₁[3]) ✓

伪造! 无需直接知道任何密钥元素。

校验和防御

你可能想知道：为什么攻击者不能通过简单地向前哈希来从单个签名中伪造？校验和可以防止这种情况。

$checksum = \sum_i (w - 1 - M[i])$

对于 $M = [7, 10, 3, 15]$ 和 $w = 16$：

$C = (15 - 7) + (15 - 10) + (15 - 3) + (15 - 15) = 8 + 5 + 12 + 0 = 25$

如果攻击者增加了一个消息数字（比如 8 而不是 7），则校验和会减少。为了伪造减少的校验和数字，攻击者需要向后哈希——这是计算上不可行的。双签名攻击绕过了这一点，因为通过两个不同的校验和，攻击者有足够的链元素来伪造校验和。

现实世界的状态管理灾难

XMSS 密钥重用漏洞不仅仅是理论上的。状态管理失败会发生：

系统崩溃：
    T₁：签名消息，状态 = 索引 5
    T₂：将签名写入网络
    T₃：——— 崩溃 ———
    T₄：重启，从磁盘重新加载（状态仍然显示索引 4！）
    T₅：使用索引 5 签名新消息（重用！）

VM 克隆：
    VM-Original：状态 = 50
    克隆 VM → VM-Copy：状态 = 50
    两个 VM 都签名 → 索引 50, 51, 52... 被两者使用

最佳实践： 原子状态更新（在返回签名之前递增并持久化），具有单调计数器的硬件安全模块，保守的索引推进，以及在状态管理很困难时使用 SPHINCS+（无状态，但签名更大）。

第四部分：精益以太坊和签名聚合的未来

什么是精益以太坊？

以太坊基金会在 2025 年宣布的精益以太坊是以太坊共识层的完整重新设计，包含四个支柱：

  1. 精益共识：重新设计以提高安全性、去中心化和秒级最终性
  2. 精益密码学：适用于 SNARK 和量子计算机的基于哈希的签名
  3. 精益治理：协议升级的战略性捆绑
  4. 精益工艺：极简主义、模块化和形式验证

零知识证明在这个新设计中起着核心作用：精益共识/堡垒模式为共识提供了后量子安全性和可扩展性，而精益执行/野兽模式为高度去中心化的区块链中的执行提供了前所未有的规模。

精益共识中的签名问题

精益以太坊旨在实现 3 插槽最终性（最终性在约 12 秒内而不是约 15 分钟内），减少质押要求（从 32 ETH 到 1 ETH，从而启用更多验证者）以及后量子安全性。这在空前的规模上带来了签名聚合的挑战。

leanSig：以太坊的后量子签名

leanSig是一种专为以太坊共识层设计的基于哈希的签名方案。它基于 XMSS/Winternitz 签名（基于哈希，量子安全），针对 SNARK 验证进行了优化，并支持 8 年的密钥寿命。

性能目标（来自精益路线图）：

指标 目标 当前 (M4 Max)
签名时间 < 0.5 毫秒 ~0.53 毫秒
验证时间 < 0.5 毫秒 ~0.19 毫秒
公钥大小 8 个元素 8 个元素
签名大小 紧凑 ~3kB

leanMultisig：使用 SNARK 聚合基于哈希的签名

leanMultisig解决了难题：如何聚合基于哈希的签名？

与 BLS 中聚合只是简单的点加法不同，基于哈希的签名需要一种根本不同的方法：

  1. 使用 SNARK（STARK）来证明 N 个单独的 XMSS 签名是有效的
  2. "聚合签名"是 SNARK 证明
  3. 验证是 SNARK 验证，而不是签名验证

在高层次上，leanMultisig 流程如下所示：

┌─────────────────────────────────────────────────────────────┐
│  验证者 1: leanSig.sign(sk₁, msg) → σ₁ (~2.5 KB)       │
│  验证者 2: leanSig.sign(sk₂, msg) → σ₂ (~2.5 KB)       │
│  ...                                                        │
│  验证者 N: leanSig.sign(skₙ, msg) → σₙ (~2.5 KB)       │
└───────────────────────┬─────────────────────────────────────┘
                        │
                        ▼
┌─────────────────────────────────────────────────────────────┐
│  聚合器 (SNARK 证明者):                                 │
│    π = PROVE("所有 N 个签名都有效")                  │
│    聚合证明 π ≈ ~100 KB (恒定大小!)             │
└───────────────────────┬─────────────────────────────────────┘
                        │
                        ▼
┌─────────────────────────────────────────────────────────────┐
│  共识:                                                 │
│    VERIFY(π) → true/false                                   │
│    一次验证，毫秒级，后量子安全        │
└─────────────────────────────────────────────────────────────┘

leanMultisig 存储库包含此基于 SNARK 的聚合方案的工作实现。它在消费者硬件（M4 Max）上对每秒聚合数百个 XMSS 签名进行了基准测试。这是最终将取代以太坊共识层中的 BLS 聚合的代码。我们将在即将发布的文章中对此进行介绍。

为什么基于哈希的签名对 SNARK 友好：

操作 BLS (EC) XMSS/leanSig (哈希)
核心操作 椭圆曲线算术 哈希函数 (SHA-256, Poseidon)
电路内成本 ~10,000+ 个约束 ~100–500 个约束
SNARK 友好? ❌ 昂贵 ✓ 高效

哈希函数是"SNARK 原生的"，因为它们由 XOR，AND 和移位构建，这些操作直接映射到算法电路。Poseidon 专门为 SNARK 设计。这里没有昂贵的模幂运算或椭圆曲线算术。

路线图：从 BLS 到 leanMultisig

2020–2025：BLS 签名（当前）
    ↓
2025–2027：混合阶段（BLS + leanSig 研究）
    ↓
2027–2030：leanSig 部署与 SNARK 聚合
    ↓
2030+：完全后量子共识

结论：地平线上的风暴

诚实的评估是，量子计算机今天无法破解 ECDSA，但这并不意味着它们在不久的将来不会破解。我们正在建设旨在持续数十年的基础设施，而密码学转换需要数年才能完成。

数字签名是加密的承重墙。每一笔交易，每一个区块，每一个证明都建立在伪造一个签名在计算上不可行的假设之上。我们研究了四种方法：用于兼容性和速度的 ECDSA，用于通过原生聚合实现可扩展性的 BLS，用于量子抗性的 XMSS，以及用于量子抗性，基于 SNARK 的聚合的 leanSig/leanMultisig。

精益以太坊倡议代表了解决这些挑战的最雄心勃勃的尝试，它结合了基于哈希的密码学和基于 SNARK 的聚合，以创建既可扩展又具有量子抗性的共识层。

每个签名方案都反映了不同的权衡。未来十年可能会看到以太坊经历所有这些方案。

进一步阅读

标准和规范

以太坊相关

精益以太坊

学术论文

实现

  • lambdaworks：用于字段算术、椭圆曲线、配对、哈希函数、SNARK 和 STARK 的 Rust 库
  • 原文链接： blog.lambdaclass.com/eth...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
lambdaclass
lambdaclass
LambdaClass是一家风险投资工作室，致力于解决与分布式系统、机器学习、编译器和密码学相关的难题。

lambdaclass

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！