1-5% 的再投资如何创造循环性、放大和级联效应 - 而无需 涉及会计上的循环交易

<blockquote class="twitter-tweet"> <a href="https://x.com/i/status/2010758673694421384">&lt;/a> </blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script>

NVIDIA 的 CEO 黄仁勋 被问到一个问题，这个问题听起来几乎很傻，直到你尝试回答它。

他正在谈论英伟达将低个位数的百分比投资于 AI 公司和合作伙伴，而采访者则追问循环性和系统性风险。黄仁勋的反应，用简单的语言来说是：这怎么可能重要？这只是很小的一部分。它不可能是驱动整个机器的东西。

对于任何做过物理学的人来说，这种反应都有一种熟悉的味道。

这是通过大小进行推理的味道。

物理学中充满了通过大小进行推理而恰恰错过了现象的例子。一个经典的例子是麦克风的尖叫声。“原因”看起来微不足道：扬声器发出的微弱声音泄漏回麦克风。但是房间里仍然充满了具有攻击性的尖叫声。如果你专注于泄漏，你会听起来很明智，但却是错误的。正确的问题不是“泄漏有多大？” 正确的问题是“环路的增益是多少？”

这是回答黄仁勋问题的唯一诚实的方法。不是争论 3% 的投资是否“小”，而是要问系统是阻尼的还是放大的。

在我们接触到小额再投资的物理学公式之前，先划定一个清晰的界限，因为知识卫生很重要。

这篇文章不是关于会计循环的。我们不是在谈论循环收入、确认游戏或任何需要法医证据的东西。在一个系统中，每个发票都是真实的，每个审计师都感到满意，你也可能存在一个危险的反馈回路。我们在这里研究的是经济循环：供应商的支持提高了客户的消费能力，从而增加了供应商的销售和现金，进而再次增加了供应商的支持。一个由普通激励和融资约束组成的循环。

• NVIDIA，$N$，销售为 AI 模型提供动力的芯片。
• 像 OpenAI 这样的合作伙伴，$P$，购买这些芯片、构建模型并发展。
• NVIDIA 将其收入的一小部分——比如 3%——再投资回这些合作伙伴。

现在，我们可以尝试从第一性原理来理解这种小额再投资的物理学：构建一个具有我们正在讨论的行为的最简单的玩具模型，检查单位，看看这个玩具模型必须做什么。

你可以用头脑掌握的机器

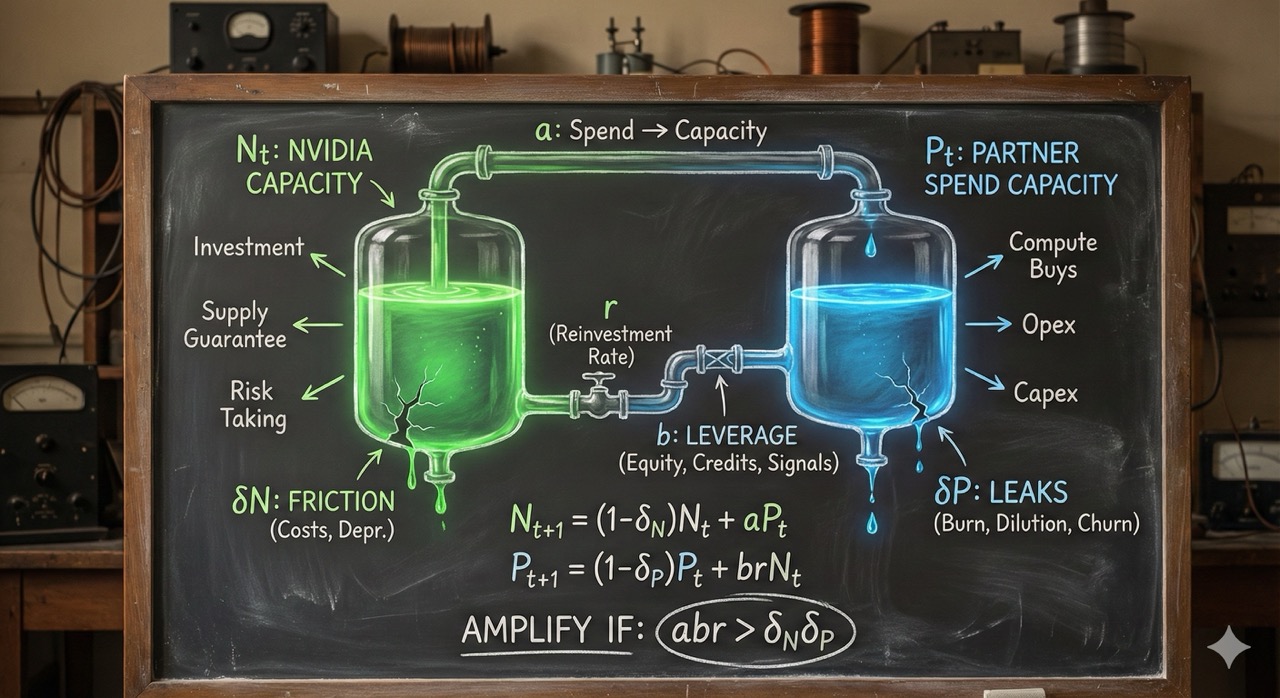
暂时忘记收入。收入是一个流量。它每个周期都会重置。像对待永远积累的股票一样对待收入，你就会不小心制造出一台永动机，然后祝贺自己发现了指数增长。

相反，追踪一些行为类似于物理状态的东西：一个水库。

将一个水库称为 $N_t$：英伟达在时间 $t$ 的可部署能力。不仅仅是银行里的现金，而是推动生态系统的实际能力 —— 投资、延长条款、补贴、保证供应、为客户提供融资、承担风险。

将另一个水库称为 $P_t$：合作伙伴在时间 $t$ 的支出能力。购买计算的能力 —— 资本支出预算、运营支出跑道、债务能力、资本市场为消耗提供资金的意愿。

现在用两个耦合连接它们。

当合作伙伴拥有支出能力时，他们会购买计算资源。其中一部分支出会转化为供应商的能力：收入变成利润，利润变成自由现金流，现金变成“我们可以做更多的事情”。

当供应商拥有能力时，它可以将一小部分回收回合作伙伴：股权支票、信贷、折扣、供应商融资、预购，任何使合作伙伴在下一个周期更有能力支出的东西。

最后，添加泄漏。真实的水库会泄漏。在市场中，泄漏是成本、竞争、折旧、失败、稀释、流失、价格压力和纯粹的坏运气。

在这一点上，你已经看到了形状：一个带有摩擦的循环。一个循环可以是一个飞轮或一声尖叫。区别在于循环放大扰动的速度是否比摩擦力消耗它们的速度更快。

最不作弊的最小方程

以离散时间编写动态（季度是一个自然的心理周期，但只要你保持一致，时间单位并不重要）：

$$ \begin{aligned} N_{t+1} &= (1-\delta_N)N_t + aPt \ P{t+1} &= (1-\delta_P)P_t + brN_t \end{aligned} $$

这看起来很无辜，但它迫使你诚实地对待每个符号的含义。

$\delta_N$ 和 $\delta_P$ 是阻尼。它们将有组织的能力转化为热量。在繁荣时期，它们看起来很小。在紧缩时期，它们会跳跃。这种跳跃稍后会很重要。

$r$ 是再投资率，黄仁勋称之为“个位数”。

$a$ 是合作伙伴的支出能力转化为供应商能力的有效程度。它隐藏了枯燥但至关重要的东西：支出的集中程度、合作伙伴的计算预算中有多少流向该供应商，以及在竞争中幸存下来的利润率。

$b$ 是人们过快挥手驱散的部分。在一个沉睡的世界里，$b$ 是“帮助你的客户的投资回报率”。在一个自反的世界里，$b$ 也是一个融资条款。供应商的支持可以改变合作伙伴筹集资金、签订租赁协议、借款或被视为可信的能力。不是因为有人在撒谎，而是因为信念会改变约束。一张小额支票可以改变更大一笔外部资本的条款，而其中一些资本会变成计算支出。

这就是一个句子中的整个机制：如果小额回收改变了别人的融资约束的斜率，那么它就可能很重要。

现在，数学提出了它直接的问题：这个耦合系统会衰减还是放大？

系统真正关心的那个数字

将方程打包成一个矩阵：

$$ \begin{bmatrix} N{t+1} \ P{t+1} \end{bmatrix}

\begin{bmatrix} 1-\delta_N & a \ br & 1-\delta_P \end{bmatrix} \begin{bmatrix} N_t \ P_t \end{bmatrix} $$

物理学家看到这个，立即想要得到主导特征值，$\lambda_{\max}$。不是因为特征值很时髦，而是因为它们告诉你一个小扰动是每个周期增长还是每个周期缩小。

在大致对称的情况下，其中 $\delta_N \approx \delta_P = \delta$，你会得到一个干净的表达式：

$$ \lambda_{\max} = (1-\delta) + \sqrt{abr} $$

现在，黄仁勋的“3% 怎么可能重要？”在没有戏剧性的情况下得到了回答。

如果 $\lambda_{\max} < 1$，冲击会缩小。循环是阻尼的。回收只是做生意的成本。

如果 $\lambda_{\max} > 1$，冲击会增长。循环会放大。即使是一个诚实的系统也可能开始以自己的反馈为食。

临界条件是：

$$ (1-\delta) + \sqrt{abr} > 1 \quad\Longleftrightarrow\quad \sqrt{abr} > \delta \quad\Longleftrightarrow\quad abr > \delta^2 $$

最后一个不等式，$abr > \delta^2$，是关键，因为它从根本上扼杀了“通过大小进行推理”。

如果你有 $\delta_N \ne \delta_P$，这个条件变成 $abr > \delta_N\delta_P$

系统不关心单独的 $r$。它关心的是 $a b r$ 的乘积与阻尼的平方相比。

你可以保持 $r$ 在个位数，但如果 $a$ 和 $b$ 足够大，或者如果你所处的制度中 $\delta$ 看起来很小，你仍然可以越过阈值。并且制度会变化。

这并不奇怪。它与麦克风、反应堆和桥梁振荡背后的逻辑相同。你不会争论一个电子是否“小”。你会问环路增益是否超过了损耗。

系统性风险实际上来自哪里

如果你在这里停止，很容易说“啊哈，泡沫”。但是这个词太生硬了。有趣的物理学不是“增长”。有趣的物理学是临界点附近的脆弱性。

当 $\lambda_{\max}$ 接近 1 时，系统会以一种特定的方式变得敏感。扰动的记忆会变得很长。冲击不会很快被遗忘。对于线性系统，一个有用的粗略估计是，灵敏度的行为类似于：

$$ \text{灵敏度} \propto \frac{1}{|1-\lambda_{\max}|} $$

不要崇拜常数。看形状。几何形状。当 $\lambda_{\max}$ 接近 1 时，分母会变小，并且系统变得敏感的速度比你的直觉预期的要快。

这就是“系统性”在诚实系统中出现的方式：不是作为一种神秘的邪恶，而是作为一种相关性。每个人都开始一起行动，因为耦合正在进行协调。当循环很强时，多样化开始失败。

请注意，什么可以快速移动 $\lambda_{\max}$：$b$ 和 $\delta$。融资条件、情绪、利率和再融资窗口可以在比工厂建设或产品周期短得多的时间尺度上改变有效阻尼和有效乘数。参数不是固定的旋钮；它们是依赖于制度的。

因此，你可能处于一个循环悄悄放大的世界中，然后一个制度转变将同一个循环翻转成一个收缩引擎。

为什么级联需要一个悬崖

到目前为止，该系统是线性和礼貌的。真正的级联是不礼貌的。当有人达到约束时，它们会发生。

合作伙伴不会平稳地“减少 7% 的支出”。他们会撞到跑道墙、违反契约、错过再融资、失去对融资窗口的访问权、受到电力可用性的限制或受到监管机构的阻止。约束生效的那一刻，方程就会改变。

你不需要一个复杂的非线性来捕捉这一点。你只需要一个悬崖。

假设存在一个最小支出能力 $P^{\min}$，低于该值融资会枯竭，并且合作伙伴无法以旧的速率保持支出。然后：

$$ P_{t+1} = \begin{cases} (1-\delta_P)P_t + brN_t, & \text{如果 } P_t \ge P^{\min},\ (1-\delta_P)P_t, & \text{如果 } P_t < P^{\min}. \end{cases} $$

现在级联变得很容易想象。

一个冲击击中了 $N_t$。回收项 $brN_t$ 缩小。$P_t$ 向下漂移。如果它越过 $P^{\min}$，泵就会关闭。然后 $P_t$ 下降得更快，这会减少 $aP_t$，这会进一步缩小 $N_t$，这会进一步减少再投资。

这意味着合作伙伴可以正常支出，直到他们达到融资阈值。在 $𝑃_{min}$ 之上，他们可以继续支出并继续获得支持；在它之下，资金枯竭，“额外流入”关闭，因此支出能力自行衰减——将轻微的冲击转变为制度改变。

飞轮变成了一个螺旋，因为制度改变了。没有发生任何不诚实的事情。循环只是在阈值上向后运行。

这就是技术意义上的“级联”的含义：动态切换。

从两个水库到一个系统

双节点模型是一个显微镜，而不是一张地图。真正的 AI 构建是一个由许多合作伙伴、许多融资渠道和许多共同依赖关系组成的网络。但是数学课并没有改变。它变成了一个矩阵故事，而不是一个 2×2 的故事。

用加权相互依赖矩阵 $W$ 替换玩具耦合。然后“它会传播吗？”变成了问题“谱半径是否小于 1？”

$$ \rho(W) < 1 \quad \text{意味着扰动逐渐消失} $$

$$ \rho(W) > 1 \quad \text{意味着扰动传播} $$

如果你见过流行病模型，这与 $R_0$ 所扮演的角色相同。低于 1 时，爆发会逐渐消失。高于 1 时，它们会传播。“系统性”只是“图携带了冲击”。

在网络中，看起来像多样化的东西可能会悄悄地变成耦合：共同的贷方、共同的超大规模企业、共同的数据中心开发商、共同的需求叙述、共同的再融资窗口。这就是你如何在平静的天气中获得许多看起来独立的节点，然后在暴风雨中一起移动。

对黄仁勋的清晰回复

黄仁勋的直觉是可以理解的：1-5% 听起来很小。但是在反馈系统中，输入的大小不是标题。

标题是环路增益是否超过了阻尼，以及系统是否在临界边界附近运行，在这种边界附近，小的参数变化会产生大的后果。

如果合作伙伴支出足够集中（$a$ 高），如果供应商支持足够改变融资约束（$b$ 高），并且如果你所处的制度中的有效阻尼较低（$\delta$ 小），那么低再投资率可能很重要。在那个世界里，“小”不会保持小。它变成了触发器。

麦克风尖叫是正确的比喻，因为它教会了正确的习惯。

不要盯着泄漏看。

测量环路周围的增益。

参考文献

• NVIDIA CEO Jensen Huang on the impact of low reinvestments

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～