FRI 协议为何有效？

FRI 协议 是当今生产环境中部署的许多 SNARKs 的关键组成部分。 有很多很棒的讲座解释了 FRI 是什么以及它是如何工作的。 其中，我强烈推荐 Dan Boneh 的 ZK Whiteboard Session 模块（S2M7，S2M8）。 对于那些喜欢更实际的介绍的人，我建议遵循一个带有配套代码的教程，例如 StarkWare 的 STARK 101 的第三部分。

在这篇文章中，我不会重复上面列出的精彩教程的内容。 我想回答这个问题：FRI 为什么是安全的？ 为什么执行此协议能让我们满意地保证证明者的初始消息接近 Reed-Solomon 码字？

这些问题通常由协议的安全证明来回答。 不用说，FRI 的安全证明不是入门级的读物。 然而，与合著者 Albert 和 Benedikt 一起，我最近尝试给出一个更简单的证明（可在 ePrint 上找到）。 这篇文章是我们所用想法的总结。

我假设读者熟悉 FRI 及其相关的工具和术语。 我将首先快速回顾协议的机制，主要是为了定义我将在全文中使用的符号。 然后我将介绍 "prover message graph"，这是 FRI 安全证明的一个有用工具。 之后，我们将讨论 FRI 中使用的 "folding" 操作的一个关键安全属性，并最终论证该协议是安全的。

FRI 回顾和符号

FRI 协议用于证明证明者函数 f0 接近给定的 Reed-Solomon (RS) 码。 它的工作原理是使用验证者挑战连续 "folding" 证明者的函数。 最终，当函数足够小时，验证者可以完整地读取它，并检查它是否是来自较小 RS 码的码字。 然后，验证者在所有证明者的消息之间执行抽查，以确保 fold 操作计算正确。

在本文中，我将使用符号 RS[F,L,d] 来表示在有限域 F 上定义的 Reed-Solomon 码，其评估域为 L⊆F∗，次数界限为 d∈N。 RS 码的速率写为 ρ=d/|L|。

具体来说，我将考虑初始域 L0 是 16 次单位根，初始次数界限是 d0=8 的例子。 连续代码在 8 次、4 次和 2 次单位根上定义，次数界限分别为 4、2 和 1。 我将写 f0,f1,f2,f3 来表示证明者消息，α1,α2,α3 来表示验证者的 folding 挑战。

跟踪证明者消息

在我们的安全分析中，我们需要注意的第一件事是，证明者可能发送了一个不是 Fold(fi,αi+1) 的函数 fi+1（即，使用挑战 αi+1 对 fi 的诚实 fold）。 为此，我们定义 prover message graph。 图的每一层代表一个评估域以及该域上的证明者消息。 当点相关时，我们可以在层之间绘制边：例如，第 0 层中的点 s 和 -s 都有一条边连接到Layer1中的点 s2。 该图如下所示。

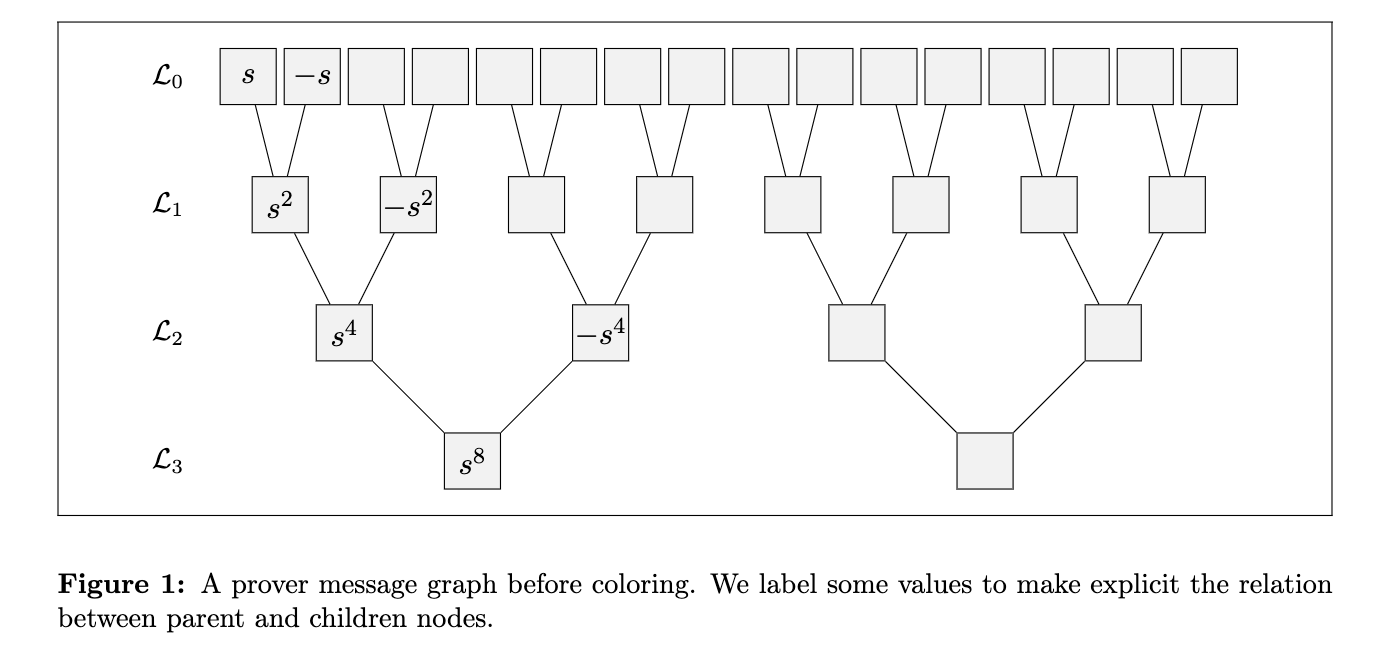
我们现在可以对图进行着色，以指示验证者运行查询阶段时会发生什么。 我们将使用绿色表示接受查询，红色表示拒绝查询。 为了执行着色，我们以 3 个节点为一组考虑节点：第 i 层中的一个节点及其在第 i-1 层中的两个亲属节点。 如果 Fold 操作在这些节点上计算正确，我们保持它们不变；否则，如果 Fold 不正确，我们用 X 标记第 i 层上的节点。 具体来说，使用上图中的标记，我们将考虑组 (s,-s,s2)，从 f0(s) 和 f0(-s) 计算 Fold(f0,α1)(s2)，如果该值与 f1(s2) 不一致，则用 X 标记节点 s2。 这正是验证者用它的检查来做的事情！

一旦我们考虑了所有三元组，我们就可以分配颜色。 所有从第 0 层中的叶子开始并以 X 结尾的路径都标记为红色（不包括 X）。 我们这样做是为了反映这样一个事实：从这样的叶子开始，验证者将不可避免地到达 X 并注意到不一致之处。 所有其他节点都涂成绿色。 下面给出一个例子。

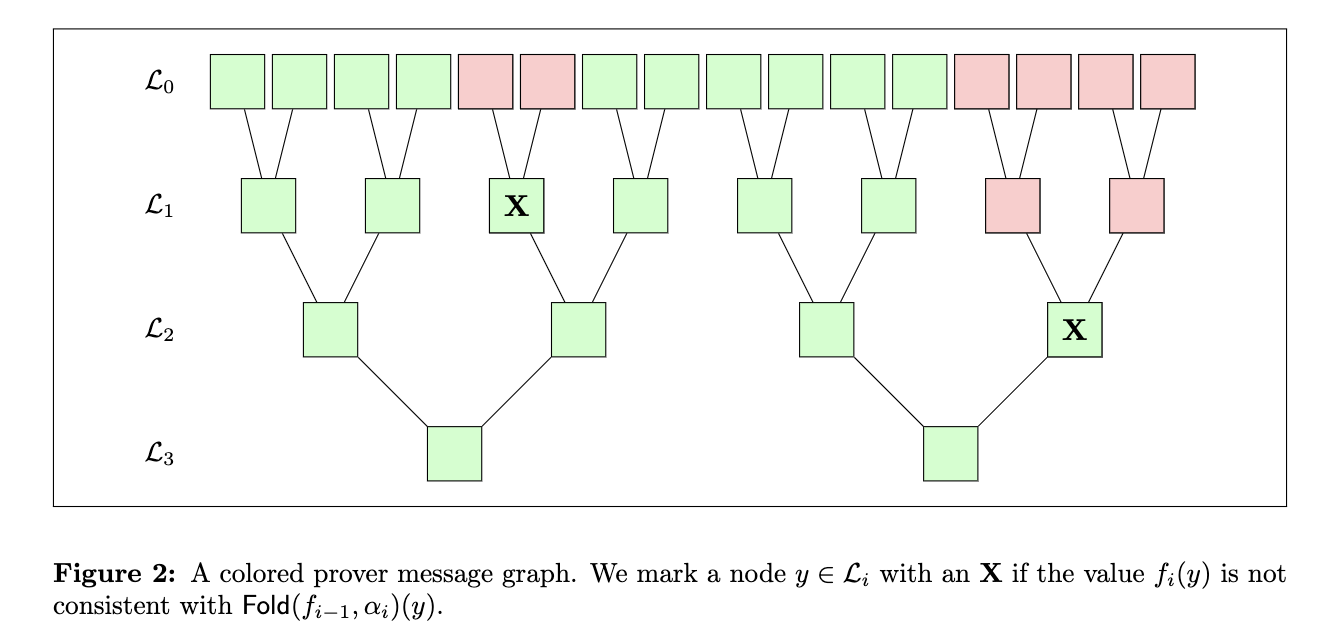
在这一点上，我想强调一些关于着色图的重要直觉：

1. 如果验证者在红色节点查询第 0 层，它将拒绝。因此，绿色节点的比例恰好是验证者接受的概率。

2. 红色从 X 向上蔓延。这意味着证明者通过不诚实地 folding 不会获得优势。此外，我们看到它这样做的越晚（例如，在最后一轮），它降低被接受的概率就越多。

3. 绿色节点的集合表示所有 folds 都是诚实执行的集合。

现在关键问题仍然存在：当第 0 层中存在大比例的绿色节点时，为什么我们可以推断出 f0 接近 RS[F,L0,d0]？正如我们接下来将看到的，这是因为验证者检查最终函数是否在最终代码中，以及 Fold 的一个重要安全属性。

Fold 的关键属性

在 FRI 交互结束时，验证者完整地读取最终函数，并检查它是否在最终代码中。 在我们的例子中，验证者读取 f3:L3→F 并检查它是否是一个常数多项式。 理想情况下，这个观察结果可以 "冒泡" 通过 prover message graph。 我们可以将一个理想的属性表述如下：

• (理想属性) 如果存在一个码字 ui∈RS[F,Li,di]，它与绿色节点上的 fi 一致，那么存在一个码字 ui−1∈RS[F,Li−1,di−1]，它与绿色节点上的 fi−1 一致。

有了这样的属性，我们的任务就可以解决了！ 我们将以归纳方式应用该属性，在图上向上移动，并发现第 0 层中绿色节点的比例至少是 f0 和码字之间的一致性。 不幸的是，事情并没有那么简单。 理想属性并不总是成立。

另一方面，我们可以做的是放宽这个属性，只要求它在验证者的 folding 挑战中 以高概率 成立。 这将产生以下真实属性：

• (真实属性) 如果 (a) 存在大比例的绿色节点，并且 (b) 存在一个码字 ui∈RS[F,Li,di]，它与绿色节点上的 fi 一致，那么在验证者消息 αi 上以高概率存在一个码字 ui−1∈RS[F,Li−1,di−1]，它与绿色节点上的 fi−1 一致。

"大比例" 绿色节点的概念是有意宽松的。 让我们表示 B⋆ 为 "足够大" 的度量。 理想情况下，我们希望 B⋆ 足够低，正如我们稍后将在论证中看到的那样（参见最终论证，情况 1）。 目前，对于 B⋆=1+ρ2 的情况，我们有令人满意的结果。 有一些私下草稿正在流传，证明了 B⋆=ρ 的情况的属性，我们甚至推测这个比例可以小到 B⋆=ρ（回想一下 ρ<1，因此 ρ<ρ）。 证明小边界的这个属性是一个开放问题，以太坊基金会正在设立高达一百万美元（!!）的奖金。

最终论证

我们现在可以使用 "真实属性" 完成我们的安全分析，该属性允许在 prover message graph 中足够大的绿色节点集合中向上冒泡一致性。 唯一的微妙之处是，我们需要处理图中任何一层绿色节点少于 B⋆ 比例的情况。 我们通过分离两种情况来论证：

1. 情况 1，存在一层 i，其绿色节点少于 B⋆ 比例。

2. 情况 2，所有层都至少有 B⋆ 比例的绿色节点。

情况 1：诚实 folds 的比例较小

我们首先考虑至少有一层无法应用真实属性的情况。 也就是说，第 i 层具有少于 B⋆ 比例的绿色节点。 等效地，该层必须至少具有 (1-B⋆) 比例的红色节点。 下图显示了 "情况 1" 的示例。

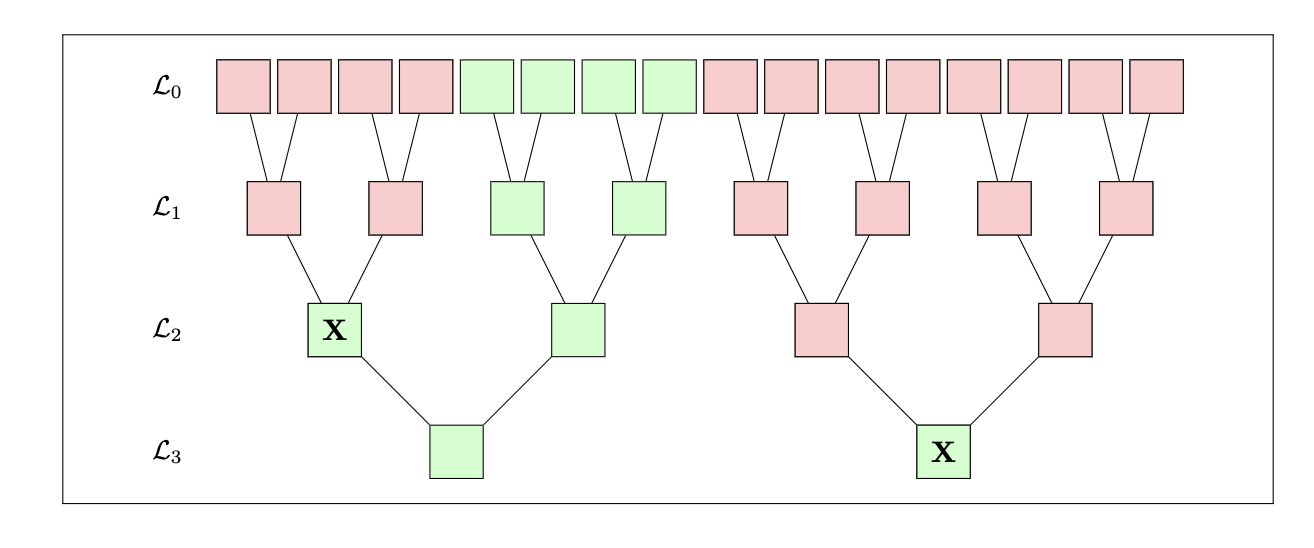
回想一下，根据我们的图着色规则，所有通向 X 的路径都标记为红色。 从这个规则，很容易确定 "红色总是向上蔓延"。 因此，我们可以证明，如果存在一层至少有 (1-B⋆) 比例的红色节点，则其上方的所有层也将至少有 (1-B⋆) 比例的红色节点。 特别是，第 0 层至少有 (1-B⋆) 比例的红色节点。

从这个讨论中，我们得出结论，第 0 层最多具有 B⋆ 比例的绿色节点，并且验证者将以概率 B⋆ 接受。 在实践中，我们希望拒绝表现得像情况 1 中的证明者，因此希望 B⋆ 尽可能小。

情况 2：诚实 folds 的比例较大

对于情况 2，我们可以参考图 2 中给出的说明。 由于绿色节点的集合足够大，我们可以应用我们的 "真实属性" 并得出结论，在 假设所有 folding 挑战都是 "好的" 的情况下，f0 和初始代码 RS[F,L0,d0] 之间的一致性至少是最顶层中绿色节点的比例。 或者，就距离（而不是一致性）而言，我们已经表明验证者的接受概率至多为 1-δ，其中 δ=Δ(f0,RS[F,L0,d0]) 是 f0 和初始代码之间的相对距离。

结论

这结束了我们对 FRI 工作原理的概述！ 该论点源于 Fold 函数的一个重要属性：当存在足够大比例的诚实 folds 时，"一致性会向上冒泡图"。 我们通过论证必须存在大比例的不诚实 folds 来处理诚实 folds 的比例不够大的情况。 在这种情况下，验证者很可能会查询它们并拒绝。

目前正在进行研究，以证明该属性对于尽可能小的 "大" 的概念成立。 这使我们能够尽可能多地停留在情况 1 中，并为我们提供更严格的安全界限。 反过来，更严格的界限使我们能够为相同的安全级别提供更短的证明，并减少证明者和验证者的工作量。

致谢

感谢 Varun Thakore, 0xteddav (David), Albert Garreta 和 Kobi Gurkan 仔细校对本文并分享许多有用的问题、更正和建议。

zkSecurity 为包括零知识证明、MPC、FHE 和共识协议在内的密码系统提供审计、研究和开发服务。

了解更多 →

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～