密码学 - Multiparty Threshold ECDSA (DKLS19)

Created: <2023-07-01 Sat>

Last updated: <2023-07-10 Mon>

Multiparty Threshold ECDSA (DKLS19)

1. 简介

2019 年，Jack Doerner, Yashvanth Kondi, Eysa Lee, and Abhi Shelat 在论文 Threshold ECDSA from ECDSA Assumptions: The Multiparty Case 中提出的多方 ECDSA 门限签名方案，简称 DKLS19 协议，本文将讨论它。

注 1：还有一个名为 DKLS18 的协议，它是 2018 年同样这 4 个作者在论文 Secure Two-party Threshold ECDSA from ECDSA Assumptions 中提出的协议，它是一个两方的 ECDSA 门限签名方案。

注 2：还有一个名为 DKLS23 的协议，它是 2023 年同样这 4 个作者在论文 Threshold ECDSA in Three Rounds 中提出的协议。

1.1. 标准 ECDSA

设 m 是待签名的消息， H(m) 是待签名消息的哈希， sk 是私钥， k 是由签名者随机生成的一次一用的随机数。

签名数据可记为 (sig,rx) ，其中 rx 是点 R=k⋅G 的 x 轴坐标， sig 由下式确定 sig≜H(m)+sk⋅rxk

2. DKLS19 主要思路

假设参与者集合为 P ，其中 |P|=t ，也就是说一共有 t 个参与者进行 ECDSA 门限签名。

DKLS19 主要思路：

1. Multiplication and Inversion. t 个参与者执行一个 “inverse-sampling” 协议（ FInvn,t ），在协议结束后，每个参与者可得到 k 的 additive sharing（即每个参与者可得到 ki ，会满足 ∑i∈Pki=k ），得到 1/k 的 additive sharing（即每个参与者可得到 vi ，会满足 ∑i∈Pvi=1/k ），以及得到 R=k⋅G 。然后每个参与者由 sk 的 additive sharing 和 1/k 的 additive sharing 进行一个类似于 GMW 乘法的协议可得到 sk∗(1/k) 的 additive sharing（即每个参与者自己手头有 ski 和 vi ，经过协议可以得到 wi ，会满足 ∑i∈Pwi=sk/k ）。

2. Consistency Check. 为了确保参与者忠实地执行上一步的协议，我们要进行一些一致性的检查。如果有参与者违法协议，则可以被发现。

3. Signing. 如果 Consistency Check 阶段没有发现问题，则我们可以说 P 中每个参与者得到的 vi,wi,R 确实会满足： ∑i∈Pvi=1/k,∑i∈Pwi=sk/k,R=k⋅G 每个参与者进行本地计算 sigi≜vi⋅H(m)+wi⋅rx 然后把它广播给其它参与者，这样每个参与者按下面式子可以得到最终的签名 sig≜∑i∈Psigi

我们容易验证这种方式得到的 sig 和标准 ECDSA 的 sig 是一样的，验证如下： ∑i∈Psigi=∑i∈P(vi⋅H(m)+wi⋅rx)=(∑i∈Pvi)⋅H(m)+(∑i∈Pwi)⋅rx=1k⋅H(m)+skk⋅rx

如何让各个参与者得到 vi 和 wi 是求解 sig 的难点。

2.1. DKLS19 协议

原论文中对 DKLS19 协议的描述如图 1 所示。

Figure 1: DKLS19

在 DKLS19 协议的 Multiplication and Inversion 阶段中，在两个重要的子协议 FInvn,t 和 F2PMull ，本文不打算详细介绍它们，感兴趣的读者可阅读原论文。本文后面会介绍一个更基础的协议 MtA，它是子协议 FInvn,t 和 F2PMull 的基础。

3. MtA with Oblivious Transfer

Alice 手头有个秘密 a ，Bob 手头有个秘密 b ，如何设计一个协议让 Alice 得到另一个值 x ，Bob 得到另一个值 y ，且满足 x+y=ab 。这个协议可以称为 Multiplicative-to-Additive（简称 MtA），它是 ECDSA 门限签名的一个关键子协议，在著名的 ECDSA 门限签名协议 GG18 协议中，是使用 Paillier 同态加密来实现 MtA 的。

在 DKLS19 中，并没有使用 Paillier 同态加密来实现 MtA，而是使用 Oblivious Transfer（OT）来实现 MtA，其思想来源于 1999 年 Niv Gilboa 发表的论文 Two Party RSA Key Generation（Gil99）。

3.1. Gil99 (OT-based MtA)

假设 a 和 b 分别是 Alice 和 Bob 手头的秘密值，它们的比特位长度是 ρ ，记 a 可以表示为二进制数 aρ−1,⋯,a1,a0 ，也就是说 a 可以表示为 a=∑i=0ρ−1ai⋅2i 。

Gilboa 设计了下面协议可以让 Alice 得到 x ，Bob 得到 y ，且满足关系 x+y=ab ：

1. Bob 随机选择 ρ 个数 s0,s1,⋯,sρ−1 ，Bob 定义 2ρ 个数 ti0≜si,ti1≜2ib+si ，其中 0≤i≤ρ−1 ；

2. Alice 和 Bob 执行 ρ 个 1-out-of-2 OT 协议。在第 i 个 1-out-of-2 OT 协议中，Bob 发送两个数 ti0,ti1 ，而 Alice 根据 ai 的值，从中选择 tiai ；

3. Alice 设置 x≜∑i=0ρ−1tiai ，Bob 设置 y≜−∑i=0ρ−1si 。

上面描述的协议可以表示为图 2 所示。

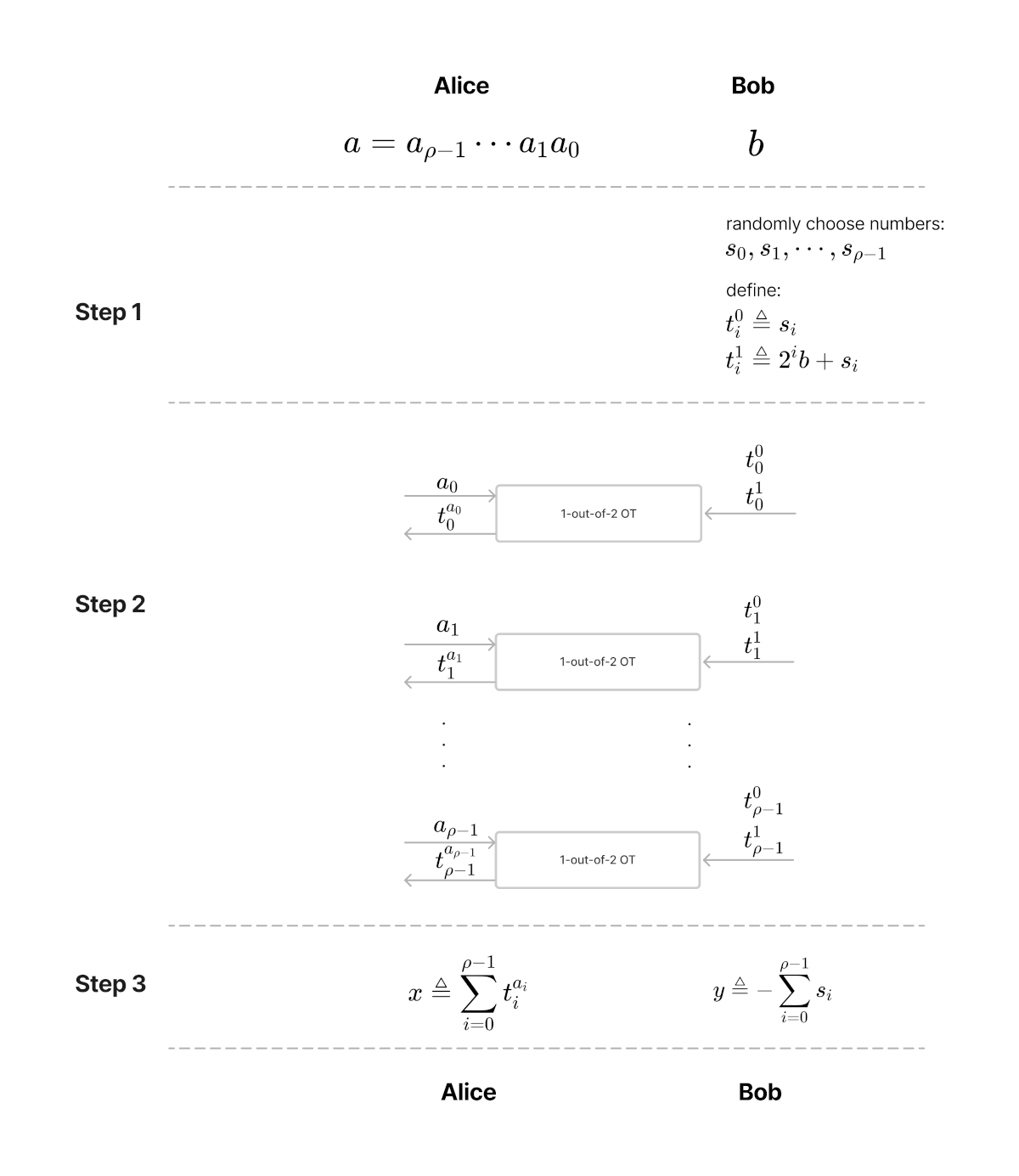
Figure 2: Gil99 (OT-based MtA)

下面来证明一下，为什么 x+y=ab 会成立。

x+y=∑i=0ρ−1tiai−∑i=0ρ−1si≡∑i=0ρ−1(ai⋅2ib+si)−∑i=0ρ−1si≡b∑i=0ρ−1(ai⋅2i)≡ba

在上面证明过程中利用了恒等式 tiai=ai⋅2ib+si ，由于 ai 是 a 的一个二进制位，我们分别设 ai=0 和 ai=1 两种情况，每种情况下容易验证这个恒等式成立。

3.2. 特点：Light Computation, Heavy Bandwidth

基于 Oblivious Transfer 的 MtA 协议有个特点：Light Computation, Heavy Bandwidth。

之所以说 Light Computation，是由于基于 Oblivious Transfer 实现的 MtA 协议的计算量要小于其它方案（如基于 Paillier 同态加密）实现的 MtA；之所以说 Heavy Bandwidth，是由于会进行多个 Oblivious Transfer 过程，需要交换的数据比较多。

4. 参考

1. Threshold ECDSA from ECDSA Assumptions: The Multiparty Case

2. Two Party RSA Key Generation

• 本文转载自： aandds.com/blog/multipar... , 如有侵权请联系管理员删除。