Vitalik: 内存访问为 O(N^[1/3])

内存访问是 O(N^[1/3])

内存访问是 O(N^[1/3])

在计算机科学中，我们经常通过描述算法的运行时间作为输入大小的函数来比较算法的效率。排序是 O(n * log(n))，这意味着对 N 个项目进行排序所花费的时间与项目数量乘以其对数成正比。矩阵乘法介于 2.37 和 2.8 之间，具体取决于算法的选择。但这些估计都与底层机器执行一些基本底层操作所需的时间模型相关。通常，算术运算（加法、乘法、除法...）被认为对于固定大小的数字需要一个时间单位，并且内存访问也被认为需要一个时间单位。

在这篇文章中，我将论证内存访问的这种选择是错误的。无论是在理论上还是在实践中，内存访问都需要 O(N^⅓) 时间：如果你的内存大 8 倍，那么读取或写入它将需要 2 倍的时间。我还将展示一个应用程序的例子，其中这一点具体重要。

理论论证

想象一下，你有一个处理器位于一堆内存的中间。处理器与任何单个内存片段对话的能力受到光速的限制，因此延迟与距离成正比。在三维世界中，你可以在距离你 2 倍的范围内容纳 8 倍的内存。

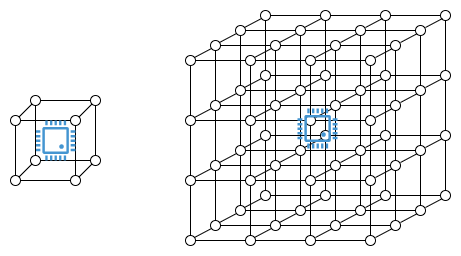
距离加倍，内存增加八倍。

这涵盖了顺序访问。当然，在实践中，CPU 并非真正位于同质内存立方体中，并且电信号并非完全以直线传播（并且，就此而言，比光慢）。但是，正如我们稍后将看到的，该模型在实践中非常接近准确。

对于并行访问，事情变得更加微妙，并且取决于介质。如果你认为读取和写入占据了一根固定长度时间内所需长度的“线”，那么你会得到相同的结果：8 倍的内存，2 倍的线长 * 时间。如果你认为它是由光制成的信号，需要消耗一定的能量，其中其强度需要考虑分散，那么 8 倍的内存意味着 2 倍的长度，这意味着单次访问需要 4 倍的能量。这可以通过让转发器在中间重复信号来缓解，但这开始让我们更接近电线。因此，O(N^⅓) 可能是更好的模型。

经验论证

现实中的计算机具有不同类型的内存：寄存器、不同级别的缓存和 RAM。我们将从这里省略 SSD/HDD，因为它们在其之上还有其他要求：不需要能量的持久存储，以及更低的每比特成本。

我们可以问一个问题：访问平均笔记本电脑具有 N 字节的某种类型的内存需要多长时间（以纳秒为单位）？这是 GPT 的答案：

事实证明，将访问时间视为访问的内存量的立方根的朴素公式使我们出奇地接近。

我们也可以对带宽做同样的事情：

请注意，这里的拟合效果要差得多，这是可以预料的：与延迟相比，带宽在很大程度上与物理原理的基本应用无关，而更多地与架构选择有关。L3 缓存的构建方式与 DRAM 的大规模吞吐量不同，因此尽管其与计算的距离更近，但其大规模吞吐量大致相同。

这在哪里重要？

我可以给出一个具体的例子，说明为什么这一切都很重要，我一年前自己遇到了这个问题：预先计算和重用中间值的各种算法的优化实现。通常，尤其是在密码学中，你有一个数学过程，涉及 N 个步骤，其中在每个步骤中，根据输入的一个比特，你要么“混合”一个特定的值，要么不“混合”。“混合”通常是结合律运算。这样的过程可以天真地在 N 个步骤中完成，如果预先计算每个步骤的 256 个值，则可以在 N/8 个步骤中完成，如果预先计算每个步骤的 65536 个值，则可以在 N/16 个步骤中完成，依此类推。这方面的例子包括椭圆曲线乘法、二进制域数学（例如，参见 我在此处的实现）以及许多其他算法。

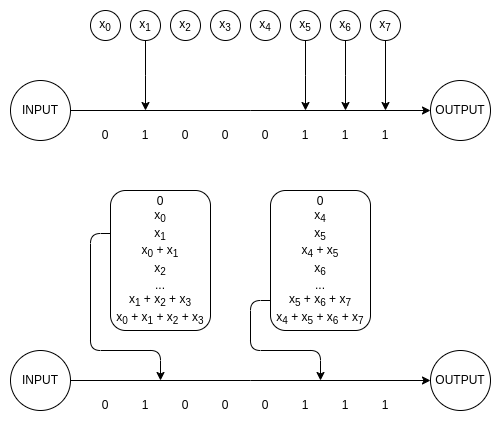
一种出奇地广泛适用的优化密码学的方法。

你应该使预计算表有多大？如果你将内存访问视为 O(1)，那么答案很明确：与你的机器拥有的一样大的内存。但是，如果你将内存访问视为 O(N^⅓)，那么它会变成一个更微妙的权衡：你必须优化 N^⅓ / log(N)，并且最佳值始终是一些“内部解”（即不是 1，也不是“尽可能多”），其确切位置取决于所涉及的常量。

在我的二进制域代码中，我发现 8 位预计算表（在该上下文中，224 个项目占用 128 MB）比 16 位预计算表（232 个项目占用 8 GB）导致更快的计算：虽然后者适合 RAM，但前者可以适合缓存，并且前者的更快访问时间是决定性的。

从长远来看，我们现在正处于接近通用 CPU 极限的时代，人们越来越多地探索用于各种任务的 ASIC。在这里，ASIC 的结构很重要。如果你可以将任务分解为多个部分，每个部分都是高度本地化的，那么每个部分中的内存访问将为 O(1)。GPU 通常已经非常擅长获得这些类型的效率。但是，如果任务需要大量的内存相互依赖性，那么你将获得大量的 O(N^⅓) 项。一个悬而未决的问题是提出一些简单的计算数学模型，但可以很好地捕捉到这些细微差别。

• 原文链接： vitalik.eth.limo/general...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～