HPU深入解析:同态加密运算如何在同态处理器上运行
- ZamaFHE
- 发布于 2025-10-04 07:48
- 阅读 1894
本文介绍了HPU(Homomorphic Processing Unit)如何执行操作,旨在为开发者提供一个清晰的HPU使用模型。HPU是一个与host CPU协同工作的PCIe协处理器,专注于密文计算,通过将整数分解为数字进行加密计算,并利用可编程自举(PBS)和密钥切换(KS)技术管理噪声,实现高效的同态加密计算。
简介
在本文中,我们将解释 HPU 如何执行操作。目标是为好奇的开发者提供一个清晰的 HPU 使用的心理模型 —— 并且,对于勇敢者,可以深入研究它的 RTL 代码。
当然,硬件永远不会单独工作。HPU 项目还包括一个软件堆栈:
- 驱动
- DMA 访问工具
- tfhe-rs + HPU 后端,用于预处理和后处理
这些组件在主机 CPU 上运行,主机 CPU 管理与 HPU 的交互。在这篇文章中,我们将专注于硬件方面,并且只在相关的地方简要提及软件。如果你对软件实现的细节感兴趣,请参考 GitHub。
规范
在深入研究硬件细节之前,让我们明确 HPU 究竟是什么以及它是如何工作的。
HPU 是一个 PCIe 协处理器芯片,与 host CPU(在此简称为“主机”)并行运行。角色分工明确:
- 主机准备密文和加密密钥,启动计算,并检索结果。
- HPU 专门专注于对密文进行计算。它不能自行加密或解密数据。
为了使这种交互成为可能,需要一种专用的协议来管理主机和 HPU 之间的通信。
整数表示
HPU 遵循与 tfhe-rs 相同的 基数表示。为什么?因为直接在 FHE/TFHE 中加密完整的整数会使密文变得巨大 —— 随着整数大小呈指数增长 —— 并且计算将很快变得不切实际。
相反,整数被分成数字,并且每个数字被单独加密。这些较小的数字密文也称为基本密文。
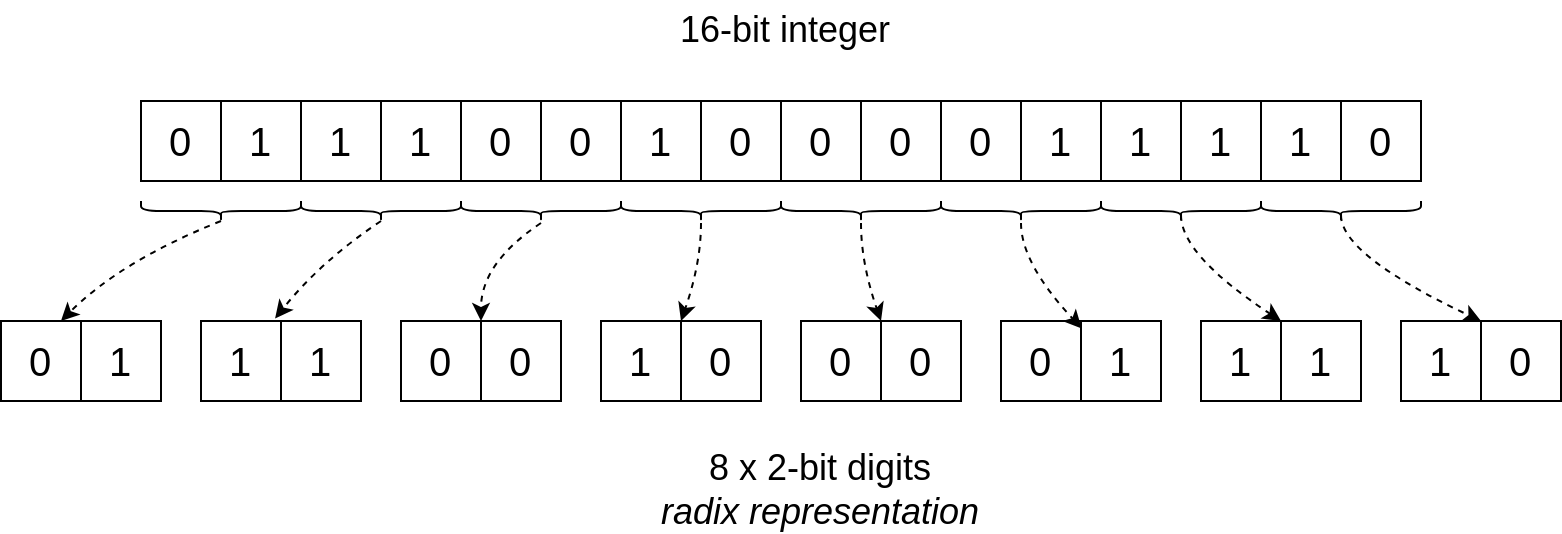
加密每个数字密文比直接加密整个整数要小得多。即使是完整的数字密文集仍然小于单个“完整整数”密文。权衡之处在于计算涉及更多的基本步骤,但是这种成本远远超过了通过减小密文大小所获得的效率。
基本密文
将基本密文视为 b 位的字。在实践中,tfhe-rs 使用编码 4 位加上 d 个 1 填充位 的密文(后者是多项式的负循环特性所必需的 —— 参见 TFHE-rs 手册 了解详细信息)。
在当前的 HPU 版本中:
- 每个整数被分解为 2 位数字(“消息”部分)。
- 4 位部分的其余 2 位保留用于计算(“进位”部分)。
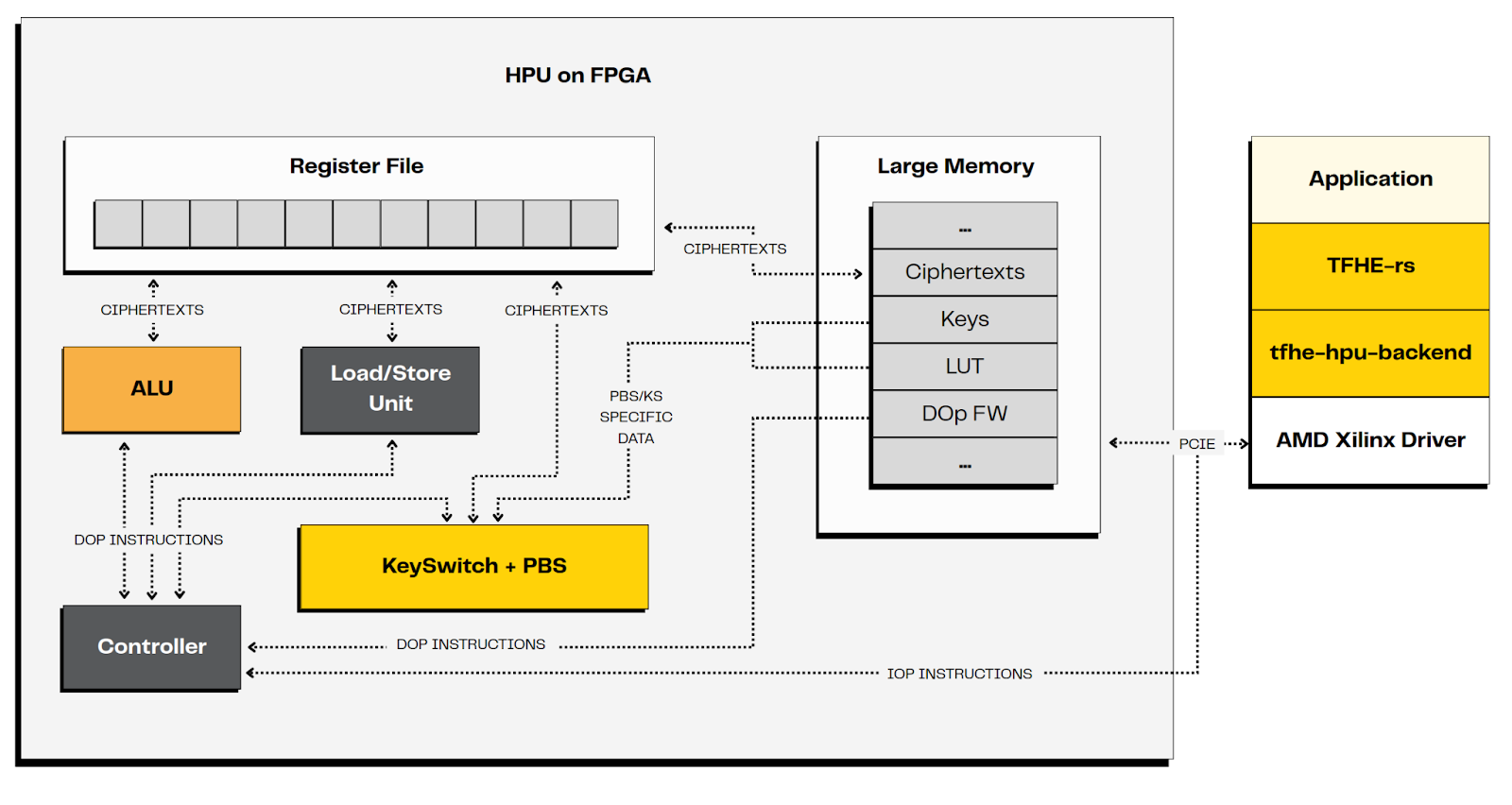
HPU 上的计算
HPU 是一个可编程处理单元,这意味着它运行用户提供的程序。由于 HPU 中的计算在数字级别上对基本密文进行操作,因此指令自然地表示为数字运算 (DOp)。
直接编写 DOp 可能很棘手,尤其是对于从完整整数的角度考虑的用户而言。为了简化这一点,HPU 可以自动将 整数运算 (IOp) 转换为相应的 DOp 代码。在实践中:
- 开发者通常提供高层 IOp 代码。
- HPU 将其转换为它可以执行的底层 DOp 代码。
- 常见的 IOp 已经带有预定义的 DOp 程序。
- 对于自定义 IOp,用户仍然可以定义自己的 DOp 并将其交给 HPU。
为了使这更容易,HPU 后端 包括用于编写和测试这些代码的工具。
HPU 与常规 CPU 有什么不同?
乍一看,HPU 看起来像一个简单的 CPU:它加载指令,处理数据并产生结果。区别在于它计算的内容:HPU 处理的是 FHE 密文,而不是普通的 16 位、32 位或 64 位整数。
然而,密文带来了一个额外的挑战:噪声。
- 在 TFHE 中,密文带有噪声。只要噪声保持在阈值以下,仍然可以正确恢复明文。
- 每个同态操作都会增加噪声。过多的噪声会导致密文变得无法使用。
这就是 自举 (BS) 的用武之地。
- 自举通过减少噪声来“刷新”密文,从而可以进行进一步的操作。
- TFHE 通过 可编程自举 (PBS) 扩展了这个想法,它不仅可以清除密文,还可以将 查找表 (LUT) 应用于该值 —— 免费。
另一个关键步骤是 密钥切换 (KS),它重新格式化密文,以便可以通过 PBS 正确处理它们。
HPU 直接在硬件中实现了 KS 和 PBS。这使得可以在 TFHE 密文上执行无限数量的计算。事实上,可用的 DOp 指令之一正是 KS + PBS。
示例:计算 |A – B|
使用 HPU 的第一步是定义你想要的 IOp,并在必要时提供其 DOp 实现。完成之后,HPU 会负责执行 —— 包括噪声管理、LUT 应用和并行分发。
让我们逐步完成一个具体的例子。
1. 编写代码
假设用户想要计算两个加密值 R=∣A−B∣ 之间的绝对差,其中 A 和 B 是两个用 TFHE 加密的 2 位密文。
如果此操作 (IOp) 在目录中尚不可用,则用户必须定义一个自定义 IOp。其签名如下:
IOP[0x01] <I2 I2> <I2@0x0> <I2@0x4 I2@0x8>在这里,此签名表示。详细信息:
- IOP[0x01]:定义具有标识符 0X01 的自定义整数运算
- <I2 I2>:指定密文地址的内存对齐规则。
- <I2@0x0>:指定存储结果的目标地址偏移量
-
<I2@0x4 I2@0x8>:指定输入。
- I2@0x4:第一个输入 (A) 存储在地址偏移量 0x4 处。
- I2@0x8:第二个输入 (B) 存储在地址偏移量 0x8 处。
(完整的 IOp 语法:docs)
在伪代码级别,该操作如下所示:
## 输入:A,B 基本密文。
## 输出:R = |A-B|,这是一个基本密文。
SEL = A > B # 布尔值
R1 = A - B
R0 = B - A
返回 (SEL ? R1 : R0)
2. 翻译成 DOp 代码
让我们编写相关的 DOp 伪代码。请记住,计算是同态执行的,这意味着实际值是未知的。另请记住,我们只有 4 位字可用。
为了在不溢出的情况下计算 x - y,我们使用伪二进制补码表示将结果限制为 3 位。在实践中,我们将其重写为:x + (‘b100 - y)。
在此,位 [2] 是符号的相反数:(0) 表示负值,(1) 表示正值。
由于比较不是算术运算,我们需要一个 LUT 来实现此功能,该功能将在 PBS 期间应用。为此,我们首先将要比较的 2 个值收集到同一个 4 位字中。
然后,PBS 输入是表示比较的 LUT 和这个字。
选择也是非算术的,因此需要另一个在 PBS 期间应用的 LUT。理想情况下,在两个 2 位值之间进行选择需要一个 5 位 LUT 输入(选择器为 1 位,数据为 2×2 位)。但是由于只有 4 位字和 4 位 LUT 可用(填充位无法使用),因此选择必须分为两个步骤:
- 步骤 1:对于每个 2 位输入,执行 PBS 以在值和0之间进行选择。
- 步骤 2:将两个结果相加。
## 输入:A,B 基本密文。
## 输出:R = |A-B|,这是一个基本密文。
S1 = (A << 2) + B # 将 A 和 B 放在同一个 4 位字中
SEL = PBS(gt, S1) # 比较 A 和 B,
# 使用带有“大于”LUT 的 PBS。
NB = 4 - B # -B 大于 3 位
NA = 4 - A # -A 大于 3 位
D1 = A + NB # A - B 大于 3 位
D2 = B + NA # B - A 大于 3 位
M1 = (SEL << 3) + D1 # 将 select 和 D1 放在同一个 4 位字中
M0 = (SEL << 3) + D0 # 将 select 和 D0 放在同一个 4 位字中
S1 = PBS(if_then_else_0, M1) # SEL ? M1[1:0] : 0
S0 = PBS(if_then_0_else, M0) # SEL ? 0 : M0[1:0]
R = S1 + S0
return PBS(clean, R) # 删除由于上次添加导致的噪声。
转换为 DOp 代码很简单:
1 LD R1 TS[1].0 # 将源#0 的 element#0(即 B)加载到 R1 中
2 LD R0 TS[0].0 # 将源#1 的 element#0(即 A)加载到 R0 中
3 MAC R4 R0 R1 4 # S1 = (A << 2) + B
4 PBS R4 R4 PbsGreaterThan # SEL = PBS(gt, D1)
5 SSUB R2 R1 4 # NB = 4 - B
6 SSUB R3 R0 4 # NA = 4 - A
7 ADD R2 R2 R0 # D1 = A + NB
8 ADD R3 R3 R1 # D2 = B + NA
9 MAC R2 R4 R2 8 # M1 = (SEL << 3) + D1
10 MAC R3 R4 R3 8 # M0 = (SEL << 3) + D0
11 PBS R2 R2 PbsIfThenElse0 # S1 = PBS(if_then_else_0, M1)
12 PBS R3 R3 PbsIfThen0Else # S0 = PBS(if_then_0_else, M0)
13 ADD R2 R2 R3 # R = S1 + S0
14 PBS R2 PbsNone # R = PBS(clean, R)
15 ST TD[0].0 R2 # 将 R2 存储在 destination#0 的 element#0 中
注意: 此自定义 IOp 作为示例显示。一种更有效的方法是使用带有 LUT 的单个 PBS,因为带有 2 位输入的 |A-B| 只是一个 4 位输入 → 2 位输出函数。
有关更多详细信息,请参见 DOp 文档。请记住,LUT 可以编码任何 4 位输入 → 4 位输出函数,如果该函数尚未在目录中,则可以定义自己的函数。
3. 在 HPU 上执行
现在让我们看一下 HPU 对此代码的执行。
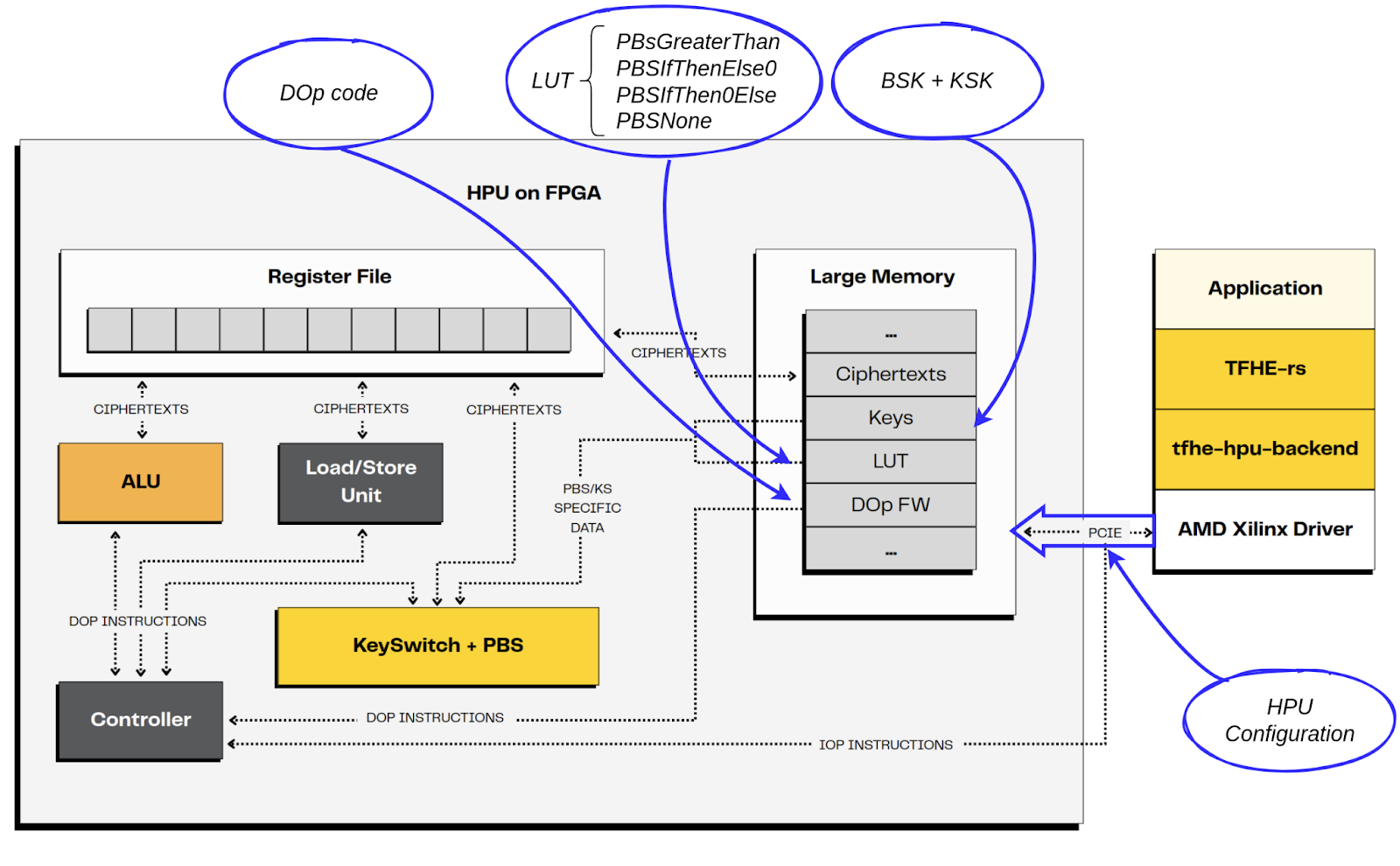
- HPU 初始化
主机为计算准备 HPU。
- 配置它。
- 加载加密密钥
- 将 DOp 加载到 HPU 内存中的程序区域中。
- 将 Dop 与自定义 IOp 0x01 相关联。
请注意,在实践中,会加载整个 DOp 目录。因此,相关的 IOp 已准备好使用。
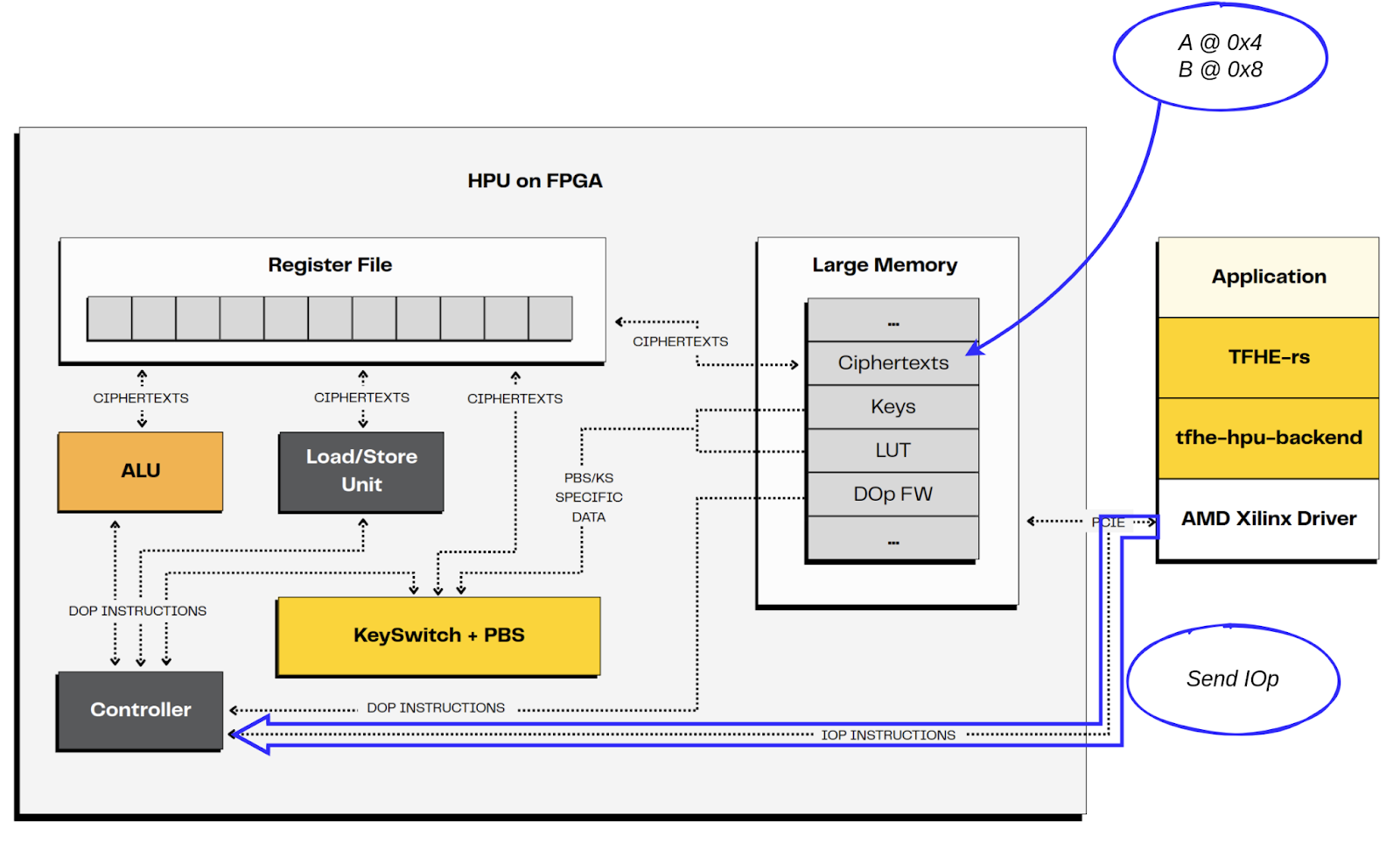
- 过程
-
主机将 A 和 B 加载到 HPU 数据内存中,偏移量分别为 0x4 和 0x8。
-
主机通过将要执行的 IOp 发送到 HPU 来启动计算。
- 执行
- IOp 由控制器转换为 DOp 代码。在当前的实现中,这包括从 IOp 标识符在内存中检索 DOp 代码。
- 控制器负责将 DOp 分发到相应的处理单元 (PE)。控制器具有前瞻窗口。它能够将独立的指令并行分发到多个 PE。DOp#4 和 #5 就是这种情况,它们是独立的,并且针对不同的 PE。
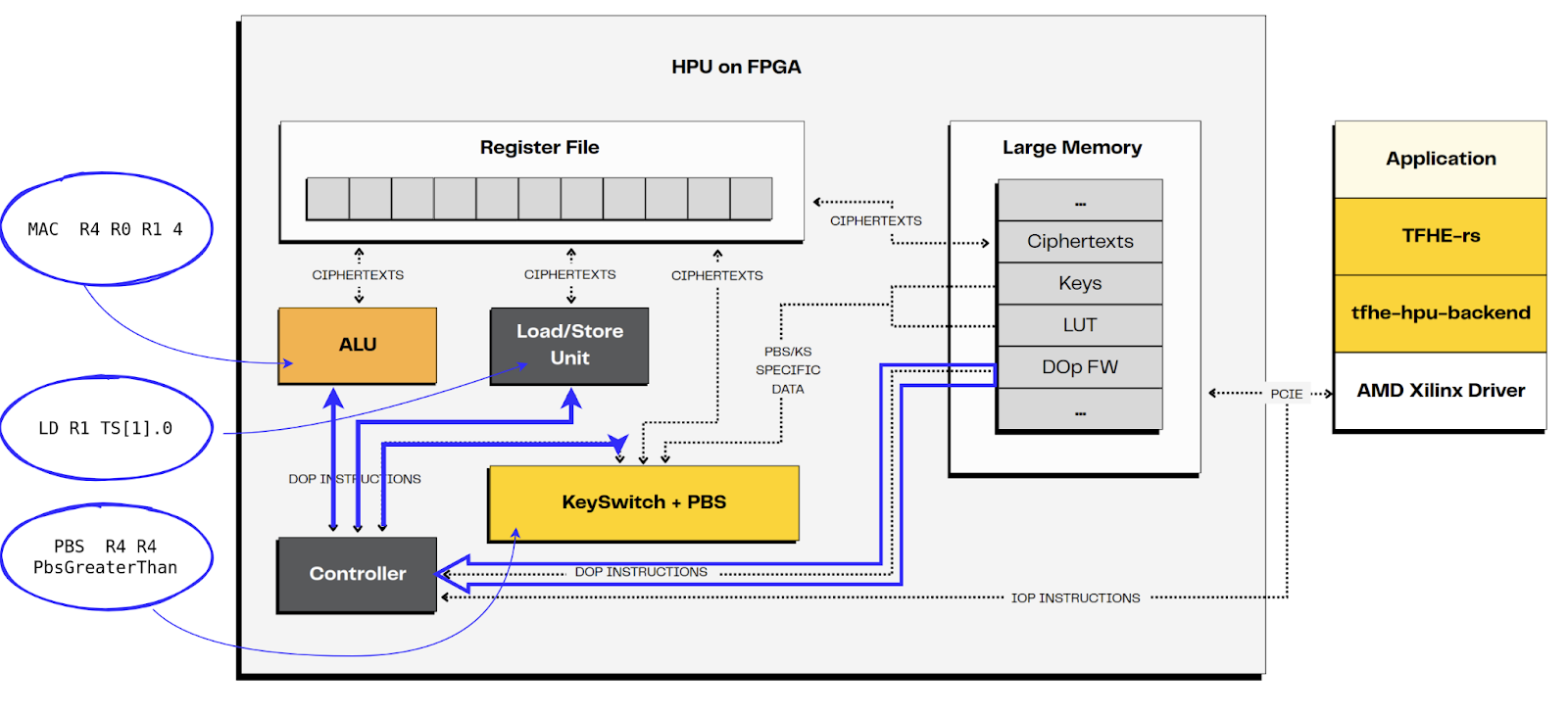
-
控制器通知主机 IOp 程序已结束。
-
主机在 HPU 数据内存中检索结果,此处偏移量为 0x0。
正如你所注意到的,使用 HPU 的第一步是定义要执行的 IOp 代码,如果该操作尚不可用,则最终定义关联的 DOp 代码。
结论
HPU 弥合了前沿密码学和硬件加速之间的差距。通过结合可编程操作 (IOp/DOp)、噪声管理 (PBS/KS) 和并行执行,它使开发人员能够高效地执行复杂的加密计算。
无论你是研究人员、开发人员还是只是好奇,你都可以立即开始使用可用的 工具 和 tfhe-rs 后端 进行实验。没有 FPGA?尝试 mockup 来模拟 HPU 行为。
剩下的就是编写一些代码了!
其他链接
- 查看 Zama HPU GitHub
- 阅读 HPU 文档
- 在 X 上关注 Zama 以获取最新消息
- 原文链接: zama.ai/post/hpu-deepdiv...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 我对 2026年隐私的论点 1085 浏览
- 基于密码学的安全联邦学习 584 浏览
- 哈希方法的构建者(以及更多) 739 浏览
- Plinko PIR 教程 1039 浏览
- 为什么数字投票系统(真正有效的)用了这么长时间才实现 2397 浏览
- 永久隐私投票即将登陆 Snapshot 963 浏览
- TFHE-hpu-backend - 用于连接HPU加速器 1358 浏览
- TFHE 密文 Bootstrapping 耗时低于 1 毫秒 1715 浏览
- ZK 月报:2025年8月回顾 1708 浏览
- DAVINCI协议白皮书 1345 浏览
- 基于RLWE的多方同态加密:当多方计算遇见同态加密 1068 浏览

