零知识证明变得简单:zkWeb 和 ZoKrates
- asecuritysite
- 发布于 2025-08-11 08:24
- 阅读 1886
本文介绍了使用zkWeb快速生成零知识证明(ZKP)的方法,zkWeb利用zokrates Javascript文件和Solidity代码生成ZKP,通过一个哈希值的例子,展示了如何使用Zokrates和Solidity来创建一个零知识证明,验证知道秘密x但无需暴露x本身,最后部署到以太坊测试网络上。

简化 ZKP:zkWeb 和 ZoKrates
最近看到了 zkWeb 的推出,它提供了一种生成零知识证明 (ZKP) 的简便方法 [ 此处]:
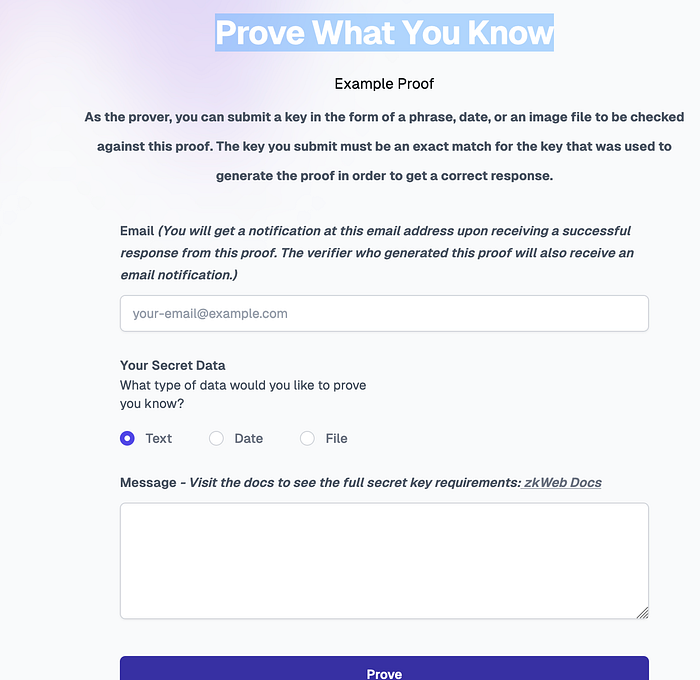
基本上,这个基础设施使用 zkokrates Javascript 文件(zokrates.js),它是用于以太坊上 zkSNARK 的 ZoKrates 工具箱的实现。基本上,验证者提交密钥(例如秘密阶段),zkWeb 创建一个 SHA-256 并将其转换为唯一的 14 位十六进制字符串。然后将此字符串传递给 zokrates.js,它使用一些 Solidity 代码来生成 ZKP。
NI-ZKP
我们生活在一个泄露过多的数字世界中。我们的系统通常设置为存储关于我们的敏感信息,并且我们也会通过我们的应用程序传递这些敏感信息。但是,还有另一种方法,那就是创建非交互式零知识证明 (NI-ZKP)。这些神奇的小函数允许我们证明我们知道一些秘密,并为此提供加密证明。
因此,让我们举个例子,佩吉有一个秘密值 x,而维克多存储了一个哈希值,使得:
y=H(x)
如果维克多使用 256 位哈希,那么我们几乎不可能仅凭 y 的知识来发现 x 的值。因此,x 可能是佩吉的密码,或者我的国民保险号码。它甚至可以是给定 256 位加密密钥的证明。
那么,让我们看看我们是否可以使用 H(x) 的知识来证明 x,并在智能合约中运行。由于智能合约可以公开值,我们需要对 x 的值保密。为此,我们转向 Zokrates 和 Solidity。
Zokrates
ZKP 自 20 世纪 80 年代中期以来就已存在,并且通常在处理要求方面很繁重。然而,一种新的家族出现了,它提供了快速而简短的证明。这就是 zkSnark(零知识简洁非交互知识论证)。总的来说,zkSnark 已被用于保护隐私的加密货币应用中,但在智能合约中也有应用。通常我们需要使用链下方法来完成证明,但 zkSnark 现在允许我们在链上证明事物——并且以高效且低成本的方式。因此,我们可以创建链下应用程序,然后将它们链接到以太坊区块链以进行证明。
生成这些证明的最快方法之一是使用 Zokrates,它可以插入到 Remix 中:
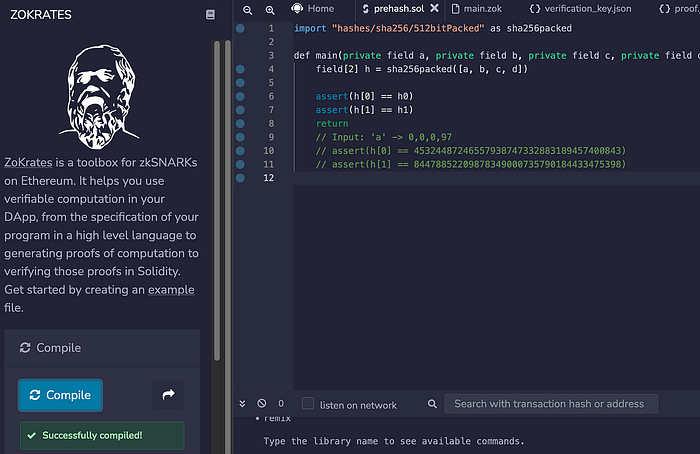
然后可以将此代码编译为 Solidity 代码。接下来给出哈希值的代码:
import "hashes/sha256/512bitPacked" as sha256packeddef main(private field a, private field b, private field c, private field d, field h0, field h1):field[2] h = sha256packed([a, b, c, d])
assert(h[0] == h0)
assert(h[1] == h1)
return// Input: 'a' -> 0,0,0,97
// assert(h[0] == 45324487246557938747332883189457400843)
// assert(h[1] == 84478852209878349000735790184433475398)在 Socrates 中,我们只能保存 128 位的值,因此我们的 256 位哈希被分成两部分。在本例中,h[0] 用于较低的 128 位,h[1] 用于较高的 128 位。对于输入数据,我们将其拆分为四个 128 位的值,这为我们提供了高达 512 位的数据输入。输入的值将是 a、b、c 和 d,其中 d 是数据缓冲区的结尾部分。与许多其他密码系统一样,我们使用 big-endian 格式,并将最后一个字节作为数据的第一个字节。因此,对于 ‘a’ 的数据输入,对于 16 个字节(128 位),我们最终得到一个十六进制值:
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 61
其中 ‘61’ 是 ‘a’ 的十六进制值。这是一个整数值 97。
有了这个,我们有四个私有字段:a、b、c 和 d。这些对于智能合约将保持私有,并且不会公开,而 h0 和 h1(哈希值)可以公开:
def main(private field a, private field b, private field c, private field d, field h0, field h1):因此,我们将为 a、b、c 和 d 创建一个零知识证明,它与 h0 和 h1 的哈希值相关。对于下一部分,我们现在需要在编译后的程序中计算一个 见证,它具有计算出的有效值。为此,我们需要为哈希生成 h0 和 h1 的值。因此,让我们以 ‘0x000….a’ 为例,然后计算两个输入哈希值(h0 和 h1):
import hashlib
x = bytes.fromhex('00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 61')
hash = hashlib.sha256(x)
hx = hash.hexdigest()
print('hx: ', hx)
hh=bytearray(hash.digest())
i1=hh[:16]
i2=hh[16:]
val1=int.from_bytes(i1,'big')
val2=int.from_bytes(i2,'big')
print (val1)
print (val2)
print ()
print (hex(val1))
print (hex(val2))这个的运行结果是:
hx: 22192dc09ba3afbc0d0c5b60675ab40b3f8e08fd3897de4e81a37a4752805f4645324487246557938747332883189457400843
844788522098783490007357901844334753980x22192dc09ba3afbc0d0c5b60675ab40b
0x3f8e08fd3897de4e81a37a4752805f46因此,见证 所需的两个整数值是:h0=45324487246557938747332883189457400843 和 h1=84478852209878349000735790184433475398。如果我们需要输入这些值,我们可以生成 见证:
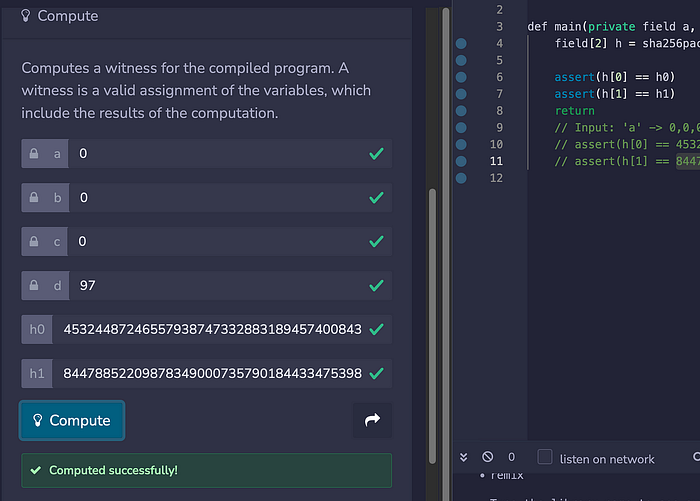
如果我们给它错误的哈希证明,我们将生成一个不正确的断言:
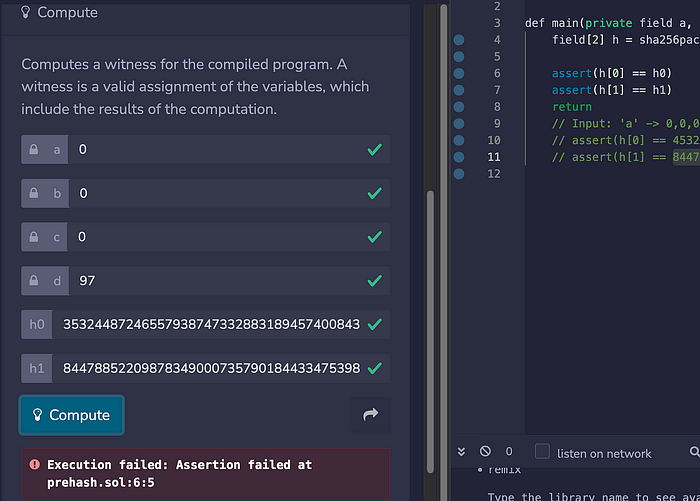
计算完成后,我们可以生成验证和证明密钥。这可能需要一分钟以上,但这是一次性的计算。为此,我们得到一个名为 verification_key.json 的文件:
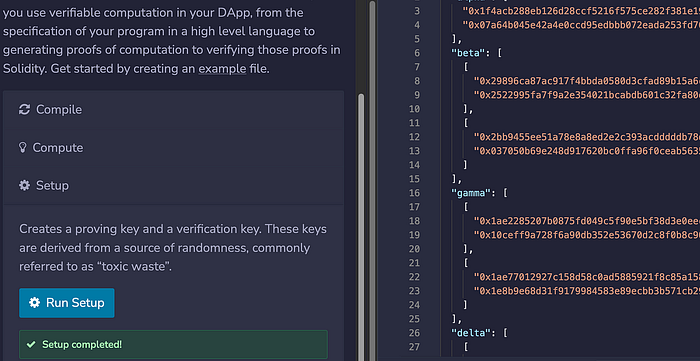
密钥是:
{
"alpha": [\
"0x1f4acb288eb126d28ccf5216f575ce282f381e19b322c3a93be96394c3659d48",\
"0x07a64b045e42a4e0ccd95edbbb072eada253fd76546b9e908ca5bb015458cacc"\
],
"beta": [\
[\
"0x29896ca87ac917f4bbda0580d3cfad89b15a6c2b2f40eefd00332eb99183a186",\
"0x2522995fa7f9a2e354021bcabdb601c32fa80ea869e91237ca8489a531e42eb7"\
],\
[\
"0x2bb9455ee51a78e8a8ed2e2c393acdddddb78dded82618aab7be32e95dc01f82",\
"0x037050b69e248d917620bc0ffa96f0ceab56356bbb00a4916ea189707b5fa87f"\
]\
],
"gamma": [\
[\
"0x1ae2285207b0875fd049c5f90e5bf38d3e0eec81615e355eb6ae86abc8e228fc",\
"0x10ceff9a728f6a90db352e53670d2c8f0b8c967713f1fd4f78faab3aaa085e82"\
],\
[\
"0x1ae77012927c158d58c0ad5885921f8c85a158d53fab02a47b55e6e34e67cee9",\
"0x1e8b9e68d31f9179984583e89ecbb3b571cb2975b687e2f1983609d24aa42eef"\
]\
],
"delta": [\
[\
"0x3044d9d51ad9fc57aa18a5609c3504fb2d81af7c29b13d2a88efd5e39fa81378",\
"0x19821f62e699a0a2d8b5e58cdb56bd5afed3921c2a1ae4141bf0c2fb6b89458b"\
],\
[\
"0x0331f36c041bf4a3370906b3c509ab6f2360172c8166025fef8e85ba61d73435",\
"0x2ccca119cbcfccc4d6de466dac8dbfeb8c53053f0b0629b73fc444036b531805"\
]\
],
"gamma_abc": [\
[\
"0x1fb042cd7e2f84f28a68723e5539525f9059c334ae477617548723d8acba6cdd",\
"0x1809fa116526d57230bd58d42333992f139969b720f3241464cd184110a8248f"\
],\
[\
"0x05a2b587d4d1c11c7fe81e9483eaa3c3c3fb7a2d7d9e1c123fa261d1b9dc1f1b",\
"0x22b9ba436a4db558617989b064a0f8d89420fb5f121b48df7cc8591e11c1ef53"\
],\
[\
"0x119a8bb852c8c5cfdb4e125660bcb22b172050148b6f9e9e3ca9280926b1cb03",\
"0x1fe6063a3a48b833156592adc8b0dde752631db2f3ab9ee5c3819c354831d583"\
]\
]
}有了验证器和证明密钥以及 见证,我们现在可以生成我们的证明:
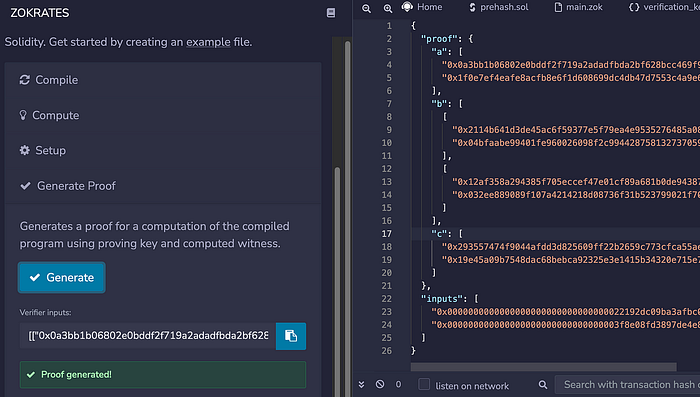
我们现在有一个验证器证明 (proof.js):
[["0x0a3bb1b06802e0bddf2f719a2adadfbda2bf628bcc469f97849f3a2009266ee1","0x1f0e7ef4eafe8acfb8e6f1d608699dc4db47d7553c4a9e6a1630ffe8236be4ee"],\
[["0x2114b641d3de45ac6f59377e5f79ea4e9535276485a0814015c4993cfa367530","0x04bfaabe99401fe960026098f2c994428758132737059ce222b4bf59347e8680"],\
["0x12af358a294385f705eccef47e01cf89a681b0de94387a35000ff85b8c99b79b","0x032ee889089f107a4214218d08736f31b523799021f700a1c80aab0e9609ed4c"]],\
["0x293557474f9044afdd3d825609ff22b2659c773cfca55ae9fe51c8b555218a0b","0x19e45a09b7548dac68bebca92325e3e1415b34320e715e7b844fb4417b1110fd"]],
["0x0000000000000000000000000000000022192dc09ba3afbc0d0c5b60675ab40b","0x000000000000000000000000000000003f8e08fd3897de4e81a37a4752805f46"]该文件的第一部分为我们提供了证明,第二部分提供了输入。我们将需要这两个部分进行测试。前四行是我们将用于证明的三元组,其余是哈希的输入:
[["0x0a3bb1b06802e0bddf2f719a2adadfbda2bf628bcc469f97849f3a2009266ee1","0x1f0e7ef4eafe8acfb8e6f1d608699dc4db47d7553c4a9e6a1630ffe8236be4ee"],\
[["0x2114b641d3de45ac6f59377e5f79ea4e9535276485a0814015c4993cfa367530","0x04bfaabe99401fe960026098f2c994428758132737059ce222b4bf59347e8680"],\
["0x12af358a294385f705eccef47e01cf89a681b0de94387a35000ff85b8c99b79b","0x032ee889089f107a4214218d08736f31b523799021f700a1c80aab0e9609ed4c"]],\
["0x293557474f9044afdd3d825609ff22b2659c773cfca55ae9fe51c8b555218a0b","0x19e45a09b7548dac68bebca92325e3e1415b34320e715e7b844fb4417b1110fd"]]
["0x0000000000000000000000000000000022192dc09ba3afbc0d0c5b60675ab40b","0x000000000000000000000000000000003f8e08fd3897de4e81a37a4752805f46"]最后,我们将使用导出一个 Solidity 智能合约:
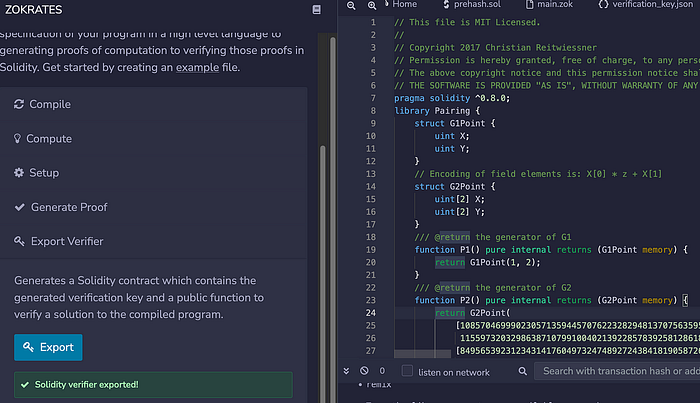
代码是:
// This file is MIT Licensed.
//
// Copyright 2017 Christian Reitwiessner
// Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
// The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
// THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
pragma solidity ^0.8.0;
library Pairing {
struct G1Point {
uint X;
uint Y;
}
// Encoding of field elements is: X[0] * z + X[1]
struct G2Point {
uint[2] X;
uint[2] Y;
}
/// @return the generator of G1
function P1() pure internal returns (G1Point memory) {
return G1Point(1, 2);
}
/// @return the generator of G2
function P2() pure internal returns (G2Point memory) {
return G2Point(
[10857046999023057135944570762232829481370756359578518086990519993285655852781,\
11559732032986387107991004021392285783925812861821192530917403151452391805634],
[8495653923123431417604973247489272438418190587263600148770280649306958101930,\
4082367875863433681332203403145435568316851327593401208105741076214120093531]
);
}
/// @return the negation of p, i.e. p.addition(p.negate()) should be zero.
function negate(G1Point memory p) pure internal returns (G1Point memory) {
// The prime q in the base field F_q for G1
uint q = 21888242871839275222246405745257275088696311157297823662689037894645226208583;
if (p.X == 0 && p.Y == 0)
return G1Point(0, 0);
return G1Point(p.X, q - (p.Y % q));
}
/// @return r the sum of two points of G1
function addition(G1Point memory p1, G1Point memory p2) internal view returns (G1Point memory r) {
uint[4] memory input;
input[0] = p1.X;
input[1] = p1.Y;
input[2] = p2.X;
input[3] = p2.Y;
bool success;
assembly {
success := staticcall(sub(gas(), 2000), 6, input, 0xc0, r, 0x60)
// Use "invalid" to make gas estimation work
switch success case 0 { invalid() }
}
require(success);
}
/// @return r the product of a point on G1 and a scalar, i.e.
/// p == p.scalar_mul(1) and p.addition(p) == p.scalar_mul(2) for all points p.
function scalar_mul(G1Point memory p, uint s) internal view returns (G1Point memory r) {
uint[3] memory input;
input[0] = p.X;
input[1] = p.Y;
input[2] = s;
bool success;
assembly {
success := staticcall(sub(gas(), 2000), 7, input, 0x80, r, 0x60)
// Use "invalid" to make gas estimation work
switch success case 0 { invalid() }
}
require (success);
}
/// @return the result of computing the pairing check
/// e(p1[0], p2[0]) * .... * e(p1[n], p2[n]) == 1
/// For example pairing([P1(), P1().negate()], [P2(), P2()]) should
/// return true.
function pairing(G1Point[] memory p1, G2Point[] memory p2) internal view returns (bool) {
require(p1.length == p2.length);
uint elements = p1.length;
uint inputSize = elements * 6;
uint[] memory input = new uint[](inputSize);
for (uint i = 0; i < elements; i++)
{
input[i * 6 + 0] = p1[i].X;
input[i * 6 + 1] = p1[i].Y;
input[i * 6 + 2] = p2[i].X[1];
input[i * 6 + 3] = p2[i].X[0];
input[i * 6 + 4] = p2[i].Y[1];
input[i * 6 + 5] = p2[i].Y[0];
}
uint[1] memory out;
bool success;
assembly {
success := staticcall(sub(gas(), 2000), 8, add(input, 0x20), mul(inputSize, 0x20), out, 0x20)
// Use "invalid" to make gas estimation work
switch success case 0 { invalid() }
}
require(success);
return out[0] != 0;
}
/// Convenience method for a pairing check for two pairs.
function pairingProd2(G1Point memory a1, G2Point memory a2, G1Point memory b1, G2Point memory b2) internal view returns (bool) {
G1Point[] memory p1 = new G1Point[](2);
G2Point[] memory p2 = new G2Point[](2);
p1[0] = a1;
p1[1] = b1;
p2[0] = a2;
p2[1] = b2;
return pairing(p1, p2);
}
/// Convenience method for a pairing check for three pairs.
function pairingProd3(
G1Point memory a1, G2Point memory a2,
G1Point memory b1, G2Point memory b2,
G1Point memory c1, G2Point memory c2
) internal view returns (bool) {
G1Point[] memory p1 = new G1Point[](3);
G2Point[] memory p2 = new G2Point[](3);
p1[0] = a1;
p1[1] = b1;
p1[2] = c1;
p2[0] = a2;
p2[1] = b2;
p2[2] = c2;
return pairing(p1, p2);
}
/// Convenience method for a pairing check for four pairs.
function pairingProd4(
G1Point memory a1, G2Point memory a2,
G1Point memory b1, G2Point memory b2,
G1Point memory c1, G2Point memory c2,
G1Point memory d1, G2Point memory d2
) internal view returns (bool) {
G1Point[] memory p1 = new G1Point[](4);
G2Point[] memory p2 = new G2Point[](4);
p1[0] = a1;
p1[1] = b1;
p1[2] = c1;
p1[3] = d1;
p2[0] = a2;
p2[1] = b2;
p2[2] = c2;
p2[3] = d2;
return pairing(p1, p2);
}
}
contract Verifier {
using Pairing for *;
struct VerifyingKey {
Pairing.G1Point alpha;
Pairing.G2Point beta;
Pairing.G2Point gamma;
Pairing.G2Point delta;
Pairing.G1Point[] gamma_abc;
}
struct Proof {
Pairing.G1Point a;
Pairing.G2Point b;
Pairing.G1Point c;
}
function verifyingKey() pure internal returns (VerifyingKey memory vk) {
vk.alpha = Pairing.G1Point(uint256(0x1f4acb288eb126d28ccf5216f575ce282f381e19b322c3a93be96394c3659d48), uint256(0x07a64b045e42a4e0ccd95edbbb072eada253fd76546b9e908ca5bb015458cacc));
vk.beta = Pairing.G2Point([uint256(0x29896ca87ac917f4bbda0580d3cfad89b15a6c2b2f40eefd00332eb99183a186), uint256(0x2522995fa7f9a2e354021bcabdb601c32fa80ea869e91237ca8489a531e42eb7)], [uint256(0x2bb9455ee51a78e8a8ed2e2c393acdddddb78dded82618aab7be32e95dc01f82), uint256(0x037050b69e248d917620bc0ffa96f0ceab56356bbb00a4916ea189707b5fa87f)]);
vk.gamma = Pairing.G2Point([uint256(0x1ae2285207b0875fd049c5f90e5bf38d3e0eec81615e355eb6ae86abc8e228fc), uint256(0x10ceff9a728f6a90db352e53670d2c8f0b8c967713f1fd4f78faab3aaa085e82)], [uint256(0x1ae77012927c158d58c0ad5885921f8c85a158d53fab02a47b55e6e34e67cee9), uint256(0x1e8b9e68d31f9179984583e89ecbb3b571cb2975b687e2f1983609d24aa42eef)]);
vk.delta = Pairing.G2Point([uint256(0x3044d9d51ad9fc57aa18a5609c3504fb2d81af7c29b13d2a88efd5e39fa81378), uint256(0x19821f62e699a0a2d8b5e58cdb56bd5afed3921c2a1ae4141bf0c2fb6b89458b)], [uint256(0x0331f36c041bf4a3370906b3c509ab6f2360172c8166025fef8e85ba61d73435), uint256(0x2ccca119cbcfccc4d6de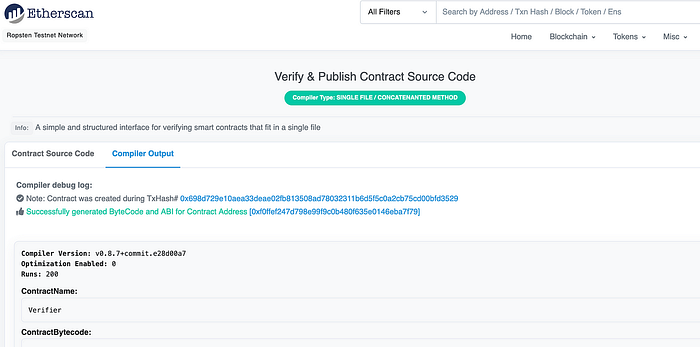
然后我们可以在测试网络上测试它\[[这里](https://ropsten.etherscan.io/address/0xf0ffef247d798e99f9c0b480f635e0146eba7f79#code)\]:
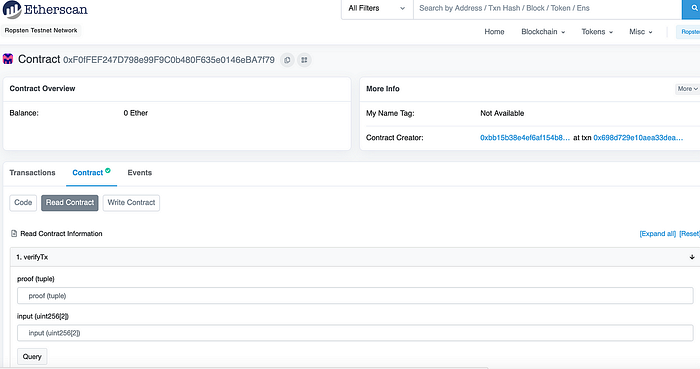
以及测试:
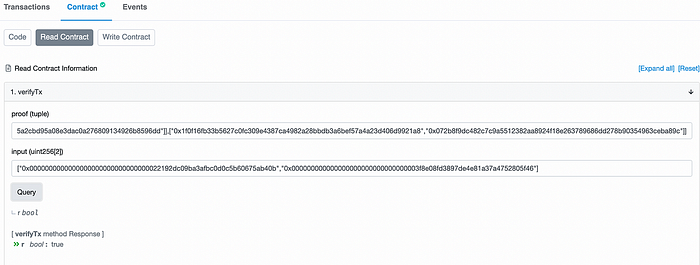
合约在这里:
[https://ropsten.etherscan.io/address/0xb3a18b87eabf5abe13cd9dcd9ee7484df2ccaffc](https://ropsten.etherscan.io/address/0xb3a18b87eabf5abe13cd9dcd9ee7484df2ccaffc)
以及(对于 0,0,0,97)的证明:
[["0x1538d0c6469863c256046d405e63952ee0d89b273ac3f9602b3581b9523470c8","0x22134f7e8bfbedba329b37b85cbf80435f266b4743ebbaa6dff577b31f99988f"],[["0x0a85811072aa12eae07d1b783717bdf5a02dadc967ad74b341acd446ba458d9f","0x2c7805c9d1ff6db5f42acb31fa88f67a07327a9a5bb2064df06fde63d109310c"],["0x27f25ac8fd5e204b53fd887667ebf3fb77165bedec4ca845bf220e1926f9dcec","0x0c9061c11b315a9d31a6a22135a5a2cbd95a08e3dac0a276809134926b8596dd"]],["0x1f0f16fb33b5627c0fc309e4387ca4982a28bbdb3a6bef57a4a23d406d9921a8","0x072b8f9dc482c7c9a5512382aa8924f18e263789686dd278b90354963ceba89c"]]
以及输入哈希值:
["0x0000000000000000000000000000000022192dc09ba3afbc0d0c5b60675ab40b","0x000000000000000000000000000000003f8e08fd3897de4e81a37a4752805f46"]
这是一个演示:
>- 原文链接: [medium.com/asecuritysite...](https://medium.com/asecuritysite-when-bob-met-alice/zkps-made-easy-zkweb-and-zokrates-f6a00b88d2e9)
>- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~- EVM Gas 分析:新的执行跟踪数据 67 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 117 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 75 浏览
- 质押和链上信贷市场之间的微妙张力 121 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 108 浏览
- Shamir份额的魔力:BLS门限签名 171 浏览
- Zcash:比特币遗忘的隐私 245 浏览
- 以太坊应该停止担心扩展性,去做人们想要的东西 225 浏览
- ZK编年史:计算模型 175 浏览
- Vitalik的L2重置:以太坊为何需要此航向修正 147 浏览
- 如何桥接到MegaETH(今天测试网,主网即将上线) 272 浏览
- Vitalik: 重新评估以太坊 Layer2 293 浏览

