有状态哈希还是无状态哈希——这是后量子问题
- asecuritysite
- 发布于 2025-07-21 09:29
- 阅读 1702
本文讨论了后量子密码学背景下,哈希签名方案XMSS和SPHINCS+。XMSS是一种有状态哈希签名方法,具有较小的密钥和快速的签名/验证速度,但密钥生成较慢;SPHINCS+是一种无状态哈希签名方法,无需记录已使用的私钥。NIST已将SPHINCS+列为标准,但XMSS仍作为一种备选方案存在。

有状态哈希还是无状态哈希 —— 这是后量子问题
几周前,我很幸运地与强大的 Ralph Merkle 进行了交谈:
当然,他是公钥密码学和 Merkle 树的共同发明人。Merkle 树的核心应用是在区块链中,我们可以将多个交易哈希到区块的根哈希。但我们也可以在数字签名中使用它,我们可以拥有许多私钥,然后将它们哈希以创建根公钥。如果我们使用私钥对消息进行签名,我们可以显示此密钥到根公钥的路径 —— 并且不能通过创建新的私钥来作弊。虽然 RSA 和 ECDSA 已成为最流行的数字签名方法,但由于量子计算机的出现,它们现在面临风险。作为一种替代方案,基于哈希的签名方法肯定是量子稳健的,所以让我们来看看其中的一种:XMSS(扩展 Merkle 签名方案)。
迈向后量子密码学
因此,NIST 已经标准化了 ML-KEM (FIPS 203)、ML-DSA (FIPS 204) 和 SLH-DSA (FIPS 205)。通过 FIPS 205,我们有 ML-DSA 的数字签名替代方案,它使用了一种称为 SPHINCS+ 的无状态哈希方法。但是,还有另一个 NIST 标准也使用基于哈希的签名 (XMSS) [此处]:

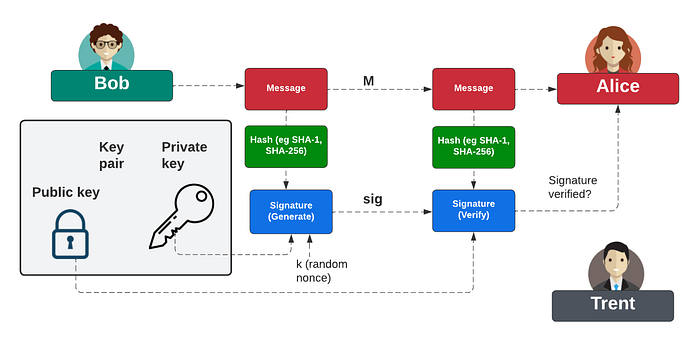
数字签名允许使用私钥创建消息签名,并使用公钥验证它。使用一次性签名 (OTS) 方案,我们只能使用给定的密钥对安全地签署一条消息,而多次签名 (MTS) 系统允许签署多条消息。
总的来说,XMSS 是一种有状态的基于哈希的方法,它产生相对较小的私钥和公钥,具有快速的签名生成和验证速度,但密钥生成速度相对较慢。Buchmann、Dahmen 和 Huelsing 在 [1] 中概述了 XMSS,并且已在 [RFC 8391] 中进行了标准化。总的来说,它使用 WOTS+ 作为其主要构建块 [此处]:

在这种情况下,我们将使用 wolfCrypt 来实现它。总的来说,基于哈希的签名方法具有相对较慢的密钥生成时间,但对于签名和验证来说相当快。对于 XMSS,三个主要的实现是 XMSS-SHA2_10_256、XMSS-SHA2_16_256 和 XMSS-SHA2_20_256。在密钥大小方面,公钥大小很小,只有 68 字节,私钥大小为 1,343 字节,签名大小为 2,500 字节。
在公钥数字签名方法中,我们将创建一个包含公钥和私钥的密钥对,然后使用我们的私钥对消息的哈希进行签名。然后可以使用我们的公钥对其进行验证:
实现
代码位于 [此处]:
##include <stdio.h>
##include <stdlib.h>
##include <stdint.h>
##include <wolfssl/wolfcrypt/xmss.h>
##include <wolfssl/wolfcrypt/wc_xmss.h>
##include <wolfssl/wolfcrypt/random.h>
##include <wolfssl/wolfcrypt/sha3.h>
char* to_hex_string(const unsigned char* array, size_t length)
{
char* outstr = malloc(2 * length + 1);
if (!outstr) return outstr;
char* p = outstr;
for (size_t i = 0; i < length; ++i) {
p += sprintf(p, "%02hhx", array[i]);
}
return outstr;
}
static enum wc_XmssRc xmss_write_key_mem(const byte* priv, word32 privSz,
void* context)
{
XMEMCPY(context, priv, privSz);
return WC_XMSS_RC_SAVED_TO_NV_MEMORY;
}
static enum wc_XmssRc xmss_read_key_mem(byte* priv, word32 privSz,
void* context)
{
XMEMCPY(priv, context, privSz);
return WC_XMSS_RC_READ_TO_MEMORY;
}
int main(int argc, char** argv)
{
XmssKey signingKey;
XmssKey verifyKey;
WC_RNG rng;
word32 publicKeySize = 0;
word32 privateKeySize = 0;
word32 signatureSize = 0;
unsigned char* sk = NULL;
unsigned char* old_sk = NULL;
int ret = 0;
char* msg= "Test"; // 消息
const char* param = "XMSS-SHA2_10_256"; // "XMSS-SHA2_16_256" "XMSS-SHA2_20_256"
byte* sig = NULL;
if (argc > 1) msg = argv[1];
int messageSize = sizeof(msg);
printf("XMSS\n");
ret = wc_InitRng(&rng);
printf("Ring initialized\n");
ret = wc_XmssKey_Init(&signingKey, NULL, INVALID_DEVID);
printf("Key initialized (signing)\n");
ret = wc_XmssKey_Init(&verifyKey, NULL, INVALID_DEVID);
printf("Ring initialized (verify)\n");
ret = wc_XmssKey_SetParamStr(&signingKey, param);
printf("Parameters set (verify)\n");
ret = wc_XmssKey_SetParamStr(&verifyKey, param);
printf("Parameters set (verify)\n");
ret = wc_XmssKey_GetPubLen(&signingKey, &publicKeySize);
ret = wc_XmssKey_GetPrivLen(&signingKey, &privateKeySize);
ret = wc_XmssKey_GetSigLen(&signingKey, &signatureSize);
ret = wc_XmssKey_SetWriteCb(&signingKey, xmss_write_key_mem);
sk = (unsigned char*)XMALLOC(privateKeySize, 0, DYNAMIC_TYPE_TMP_BUFFER);
old_sk = (unsigned char*)XMALLOC(privateKeySize, 0, DYNAMIC_TYPE_TMP_BUFFER);
(byte*) sig = (byte*)XMALLOC(signatureSize, 0, DYNAMIC_TYPE_TMP_BUFFER);
XMEMSET(sk, 0, privateKeySize);
XMEMSET(old_sk, 0, privateKeySize);
XMEMSET(sig, 0, signatureSize);
ret = wc_XmssKey_SetReadCb(&signingKey, xmss_read_key_mem);
ret = wc_XmssKey_SetContext(&signingKey, (void*)sk);
printf("Making key\n");
ret = wc_XmssKey_MakeKey(&signingKey, &rng);
printf("Signing\n");
ret = wc_XmssKey_Sign(&signingKey, sig, &signatureSize, (byte*)msg, messageSize);
/* Export the public key to a verify key. */
ret = wc_XmssKey_ExportPub(&verifyKey, &signingKey);
byte *pub_raw = malloc(publicKeySize);
ret = wc_XmssKey_ExportPubRaw(&signingKey,pub_raw, &publicKeySize);
printf("Message: %s\n", msg);
printf("Param: %s\n", param);
printf("Public key size: %d\n", publicKeySize);
printf("Private key size: %d\n", privateKeySize);
printf("Signature size: %d\n", signatureSize);
printf("Message size: %d\n\n", messageSize);
printf("Private (First 100 bytes): %s\n\n", to_hex_string(sk, 200));
printf("Public key: %s\n\n", to_hex_string(pub_raw, publicKeySize));
printf("Signature (First 100 bytes): %s\n\n", to_hex_string(sig, 200));
ret = wc_XmssKey_Verify(&verifyKey, sig, signatureSize, (byte*)msg, messageSize);
if (ret == 0) {
printf("\nSignature verified\n");
}
wc_XmssKey_Free(&verifyKey);
return 0;
}一个示例运行位于 [此处]:
XMSS
Ring initialized
Key initialized (signing)
Ring initialized (verify)
Parameters set (verify)
Parameters set (verify)
Making key
Signing
Message: Hello
Param: XMSS-SHA2_10_256
Public key size: 68
Private key size: 1343
Signature size: 2500
Message size: 8
Private (First 100 bytes): 00000001f4aba741d52b92dbb1279cdf6b74bebd07c46afc7373d9dc8961a1df6e2e747ac39b585c2583701b415b24b7ac908e8ec62c311cdc290fd2c9f62e164f322b5ad0dd981fd4ad293edd15a08ccc5d2d6cf8ac66e76d7617a73275b443321569ce062794766cbc51ca9801edb148e160658f543b97fe2fb7b7efcf95de830457fe0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Public key: 00000001d0dd981fd4ad293edd15a08ccc5d2d6cf8ac66e76d7617a73275b443321569ce062794766cbc51ca9801edb148e160658f543b97fe2fb7b7efcf95de830457fe
Signature (First 100 bytes): 00000000206aced7d8e8b0c7af481de00acc9901431278244b5a5d9e15325b5104fff163a647765693d998e5ad5bed9e9ff644dcc06f58728ba1c7ec2f0c07bbcc4d09edd2d70fc28b882bfec917c6bafedc6be499b729e836a8f01c3b2e1f79121c55f3c9df704ec11489220b9c7eef5bbc53923b918efa10157a6e313dcf03e7161d383c4678f261a2ba094527847010c7413db01b0833808931b149ac9a3140c28f8f2acb99c51e1636d99160554677ec4c329994b39705a14bf7f8fa868b9a3407ba965edfffLamport
1979 年,Leslie Lamport 定义了一种一次性签名的方法:
- 我们创建两个数据集,其中包含 256 个随机的 256 位数字(集合 A 和集合 B)。这些是私钥(512 个值)。
- 我们获取每个随机数的哈希值。这将给出 512 个哈希值,并将作为公钥。
- 然后我们对消息进行哈希处理,并测试哈希的每一位(0 … 255)。如果它是 0,我们使用集合 A 中的第 i 个数字,否则我们使用集合 B 中的第 i 个数字。
- 然后,签名是 256 个随机数(从集合 A 或集合 B 中获取),公钥是 512 个哈希值(集合 A 和集合 B 的哈希值)。
然后公钥和私钥的大小均为 16KB。该方法的演示位于 此处。
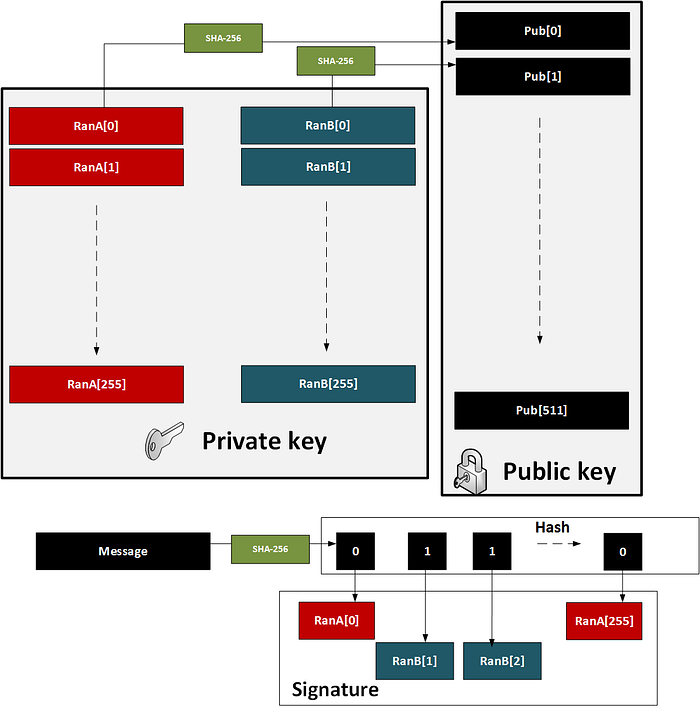
图 1:Lamport 方法
问题: 该方法的主要问题是每条消息都需要一个新的密钥对。1979 年定义的解决方案是使用 Merkle 树。
一次性签名 (W-OTS)
为了提高性能方法(并减少密钥大小),Merkle 提出了 Winternitz OTS(以 Robert Winternitz 命名)。使用此方法,可以同时签署多个位。方法是:
- 我们创建 32 个 256 位随机数。这 32 个值将是我们的私钥。
- 然后我们将每个这些值哈希 256 次。这 32 个值将是我们的公钥。
- 现在我们获取消息并使用 SHA-256 对其进行哈希处理。这将产生 32 个 8 位值(N1、N2 … N32)。
- 接下来,我们获取消息哈希中的每个 8 位值,然后哈希 256-N 次(其中 N 是 8 位值的值)。
- 为了证明签名,我们获取消息并使用 SHA-256 对其进行哈希处理,然后获取每个 8 位值。然后,我们将 8 位签名值与消息哈希值定义的次数进行哈希处理(N1、N2..)。每次操作的结果应等于公钥值。
如图 2 所示。该方法的演示位于 此处。
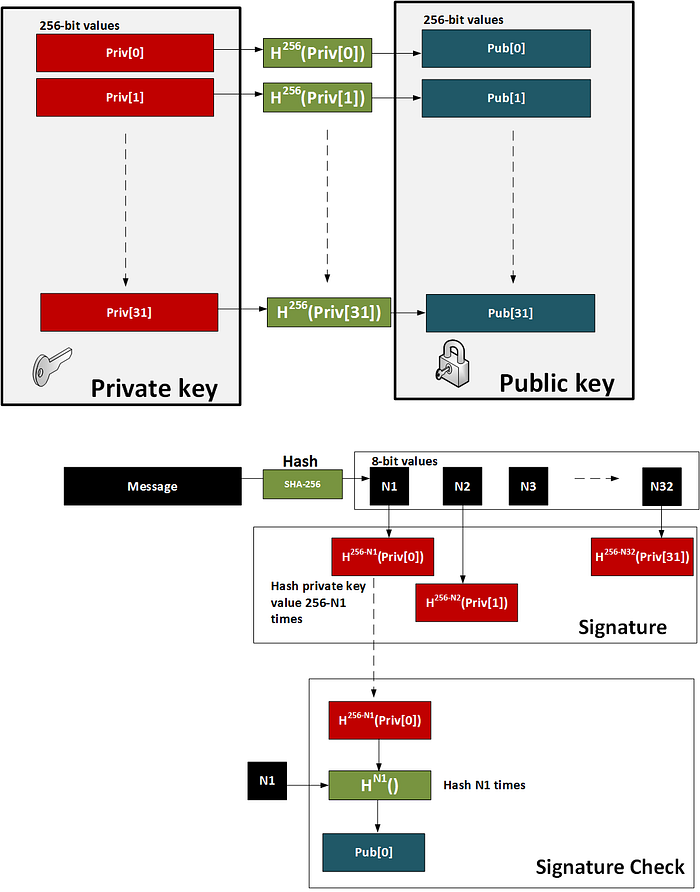
图 2:W-OTS
Merkle 树
基于哈希的方法的根源在于 Merkle 树,它是一种在许多应用程序中使用的哈希方式,包括 Bitcoin、Ethereum、Git 分布式系统、No SQL 以及许多 P2P 应用程序。对于 Merkle 树(如图 3 所示),我们获取我们的数据元素。然后我们对它们进行哈希处理,并获取这些哈希的对来创建一个新的哈希,并构建一个表。树的顶部是根元素(在本例中为 Root),它是 H1 和 H2 的哈希值。然后 H2 是 H5 和 H6 的哈希值,依此类推。然后我们可以发布 Root,但不透露任何其他哈希值。此根哈希将证明我们知道所有其他哈希值。
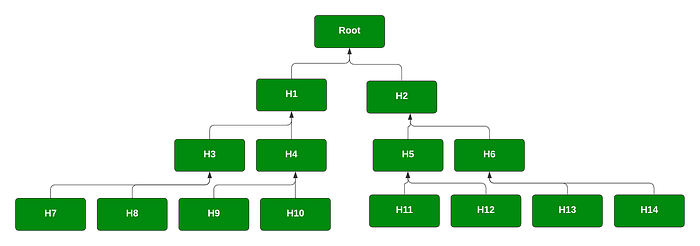
图 3:Merkle 树
如果我们想将 H7 作为私钥泄露,那么我们将发布从 H7 到 Root 的路径。作为一种核心方法,Merkle 签名方案 (MSS) 存在严重的性能和内存问题,但增强的方法(如 XMSS [2])的性能损失要小得多。2018 年,它在 RFC 8391 [3] 中进行了标准化:

问题: XMSS 是有状态的,我们需要记住我们用来签署消息的私钥,并且不要重复使用它们。这由 SPHINCS [4] 解决,它使用了 XMSS 的主要方法,但消除了状态。
结论
SPHINCS+ (FIPS 205) 当然是更好使用的方法,因为我们不需要跟踪我们使用的私钥。但是 XMSS 仍然是 NIST 定义的替代方案,并且可能有一些有用的用例 —— 尤其是在担心 lattice 方法的稳健性的情况下。
参考文献
[1] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [论文]
[2] Buchmann, J., Dahmen, E., & Hülsing, A. (2011, November). XMSS-a practical forward secure signature scheme based on minimal security assumptions. In International Workshop on Post-Quantum Cryptography (pp. 117–129). Springer, Berlin, Heidelberg.
[3] Hülsing, A., Butin, D., Gazdag, S., Rijneveld, J., & Mohaisen, A. (2018). XMSS: extended Merkle signature scheme (No. rfc8391).
[4] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., … & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368–397). Springer, Berlin, Heidelberg.
[5] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129–2146).
[6] Castelnovi, L., Martinelli, A., & Prest, T. (2018, April). Grafting trees: a fault attack against the SPHINCS framework. In International Conference on Post-Quantum Cryptography (pp. 165–184). Springer, Cham.
- 原文链接: medium.com/asecuritysite...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 量子计算与区块链:匹配紧迫性与实际威胁 88 浏览
- 基于哈希函数的签名(四):XMSS 和 SPHINCS 376 浏览
- 基于哈希函数的签名(二):少量次数签名 542 浏览
- Zig 签名(Ed25519 和 ECDSA) 729 浏览
- 基于哈希函数的签名(一):一次性签名 563 浏览
- 2026年:PQC密钥交换启动 369 浏览
- 2026年:PQC签名迁移的启动 958 浏览
- ECDSA确定性签名 746 浏览
- 各后量子密码学算法安全性评估 891 浏览
- 区块链基础设施:不为人知的真相 597 浏览
- EIP712 结构化数据签名 920 浏览
- 以太坊智能合约中的数字签名 1257 浏览

