为什么PQC加密没有选择McEliece？

asecuritysite
发布于 1天前
阅读 69

文章讨论了后量子密码（PQC）加密方案中，为何NIST没有标准化McEliece方法，尽管McEliece方法安全性高，但密钥生成速度慢，公钥尺寸大。文章介绍了Classic McEliece的参数和性能，并给出了代码示例，最后总结了McEliece方法在后量子密码学中的地位。

![](https://img.learnblockchain.cn/2025/07/20/1ee1z5CvW9rtYmV6cvnPqXw.png)

## 为什么不选择 McEliece 作为 PQC 加密？

对于 PQC 数字签名，我们有包括 ML-DSA (Dilithium)、SLH-DSA (SPHINCS+) 和 FL-DSA (FALCON) 在内的各种方法，可以很好地覆盖。SLH-DSA 的巨大优势在于，它为 ML-DSA 和 FL-DSA 的格密码方法提供了一种替代方法。这意味着，如果在格密码中发现缺陷，我们可以直接转向 SLH-DSA。

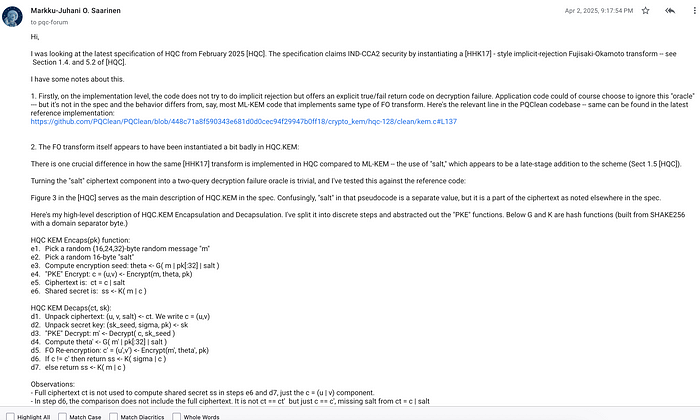
但是，在 PQC 加密/密钥封装方面，NIST 只有一个已定义的标准：ML-KEM (Kyber)/FIPS 203。因此，在 2025 年 3 月，它还宣布 HQC 将被标准化，但 HQC 团队宣布 HQC 存在一些设计缺陷 \[ [here](https://groups.google.com/a/list.nist.gov/g/pqc-forum/c/Wiu4ZQo3fP80?pli=1.For.)\]：

![](https://img.learnblockchain.cn/2025/07/20/1d8Hn2sVtHrceG6CBnRakGw.png)

因此，我们正在等待 HQC 的更新，目前只能使用 ML-KEM，并且没有替代方案。或许令人惊讶的是，NIST 没有直接推进 McEliece 方法的标准化，因为它已经存在了几十年，并且已经证明了其安全级别。虽然它在密钥生成方面确实非常慢，但在封装和解封装方面却相当不错。公钥也相当大，但生成的密文却相当小。它当然会在加密数据方面的应用有限，但它的安全性将是坚如磐石的，并且肯定是 ML-KEM 的替代方案。

## Classic Mceliece

Classic Mceliece 有五种主要模式：McEliece348864、McEliece460896 524、McEliece6688128、McEliece6960119 和 McEliece8192128。有了这些，我们有了很大的公钥和相对较大的私钥，但密文大小很小：

```
Type      Public key size (B)   Secret key size (B)  Ciphertext size (B)
McEliece348864    261,120              6,492                  196  Code based
McEliece460896    524,160             13,608                  156  Code based
McEliece6688128 1,044,992             13,932                  208  Code based
McEliece6960119 1,047,319             13,948                  194  Code based
McEliece8192128 1,357,824             14,120                  208  Code based
```

不幸的是，它在密钥生成方面很慢，但提供了可接受的封装和解封装性能：

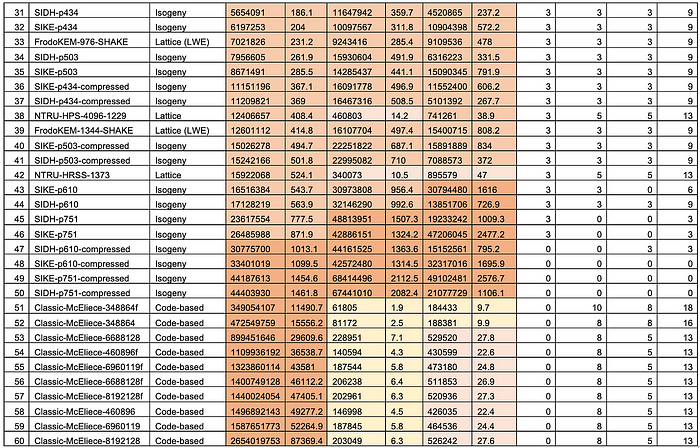
![](https://img.learnblockchain.cn/2025/07/20/0bzfzUN5ciFW-xZWp.png)

我们可以实现为 \[ [here](https://asecuritysite.com/csharp/bc_cmce)\]：

```csharp
namespace Cmce
{
    using Org.BouncyCastle.Pqc.Crypto.Cmce;
    using Org.BouncyCastle.Security;
    class Program
    {
        static void Main(string[] args)
        {
try {
                var size="mceliece460896r3";
                if (args.Length >0) size=args[0];
                var random = new SecureRandom();
                var keyGenParameters = new   CmceKeyGenerationParameters(random, CmceParameters.mceliece348864r3);
                if (size=="mceliece460896r3") keyGenParameters = new CmceKeyGenerationParameters(random, CmceParameters.mceliece460896r3);
                else if (size=="mceliece6960119r3") keyGenParameters = new CmceKeyGenerationParameters(random, CmceParameters.mceliece6960119r3);
               else if (size=="mceliece6688128r3") keyGenParameters = new CmceKeyGenerationParameters(random, CmceParameters.mceliece6688128r3);
               else if (size=="mceliece8192128r3") keyGenParameters = new CmceKeyGenerationParameters(random, CmceParameters.mceliece8192128r3);
                var CmceKeyPairGenerator = new CmceKeyPairGenerator();
                CmceKeyPairGenerator.Init(keyGenParameters);

var aKeyPair = CmceKeyPairGenerator.GenerateKeyPair();
                var aPublic = (CmcePublicKeyParameters)aKeyPair.Public;
                var aPrivate = (CmcePrivateKeyParameters)aKeyPair.Private;

以及示例运行 \[ [here](https://asecuritysite.com/csharp/bc_cmce)\]：

```
Cmce-mceliece8192128
Private key length:  14120 bytes
Public key length:  1357824 bytes
Ciphertext length:  208 bytes

Alice private (first 50 bytes): 10FCB7ACD5F28BA1371728D4F8A4468E40C88306CF5505B841E984A86F6AF725FFFFFFFF00000000A405F8015B05380E6718
Alice public (first 50 bytes): 81E5EEDA642A34955CF33D5C4FBD9A400862BF4593DF255F5BBBEC9B6EC805861A9946A8B90D2635C812A7DE7B993D9A034E
Cipher (first 50 bytes): 5C911606AFDB30BA16F914364DF2B1949C19A827FF70BC8B64B03AD0F2C9AE53FD1C3A4161EE01632358EF851D00047F334A
Bob secret:  FCBAE584DA20AD5A17827D1BA233331169E9BA11B4369F91F43CBCADD91B128E
Alice secret:  FCBAE584DA20AD5A17827D1BA233331169E9BA11B4369F91F43CBCADD91B128E
```

这里有更多的例子：

[**McEliece 公钥加密方法（后量子鲁棒）** ](https://asecuritysite.com/mceliece/)

### Robert J. McEliece

我们生活在一个由大型（且无名的）公司主导的世界中，但通常是个人建立我们的信息世界。其中一位是 Robert J. McEliece，他于 2019 年 5 月去世，享年 76 岁。在从事一系列与太空相关的项目时，他为包括信息传输和存储在内的许多领域做出了贡献。Robert 最终因其工作而被授予 Claude E. Shannon 奖，并发表了许多令人难忘的演讲。他最著名的工作是围绕纠错码，包括Rollup码，现在他的工作引起了极大的关注，即创建一种能够抵抗量子计算机的加密系统。

我们的许多公钥方法都是基于离散对数，而离散对数又是建立在约翰·纳皮尔 (John Napier) 创建的理论之上的。比特币、Tor、智能卡、Wi-Fi 和许多其他应用程序都使用离散对数。但是这些方法以及其他公钥方法都面临着来自量子计算机的风险。一个竞争者是 McEliece 密码方法。

在给任何现代研究人员的一个教训中，罗伯特·麦克利斯 (Robert McEliece) 仅用了两页纸，就在 1978 年概述了一种基于代数编码的公钥加密方法——现在称为 McEliece 密码方法 \[ [paper](http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19780016269.pdf#page=123)\]. 它是一种非对称加密方法（具有公钥和私钥），当时看起来是活板门方法的有力竞争者。不幸的是，RSA 成为山丘之王，而 McEliece 方法被推到了设计者的队列末尾。

![](https://img.learnblockchain.cn/2025/07/20/17878561_image.jpg)

它基本上漂移了近 40 年。但是，随着量子计算机时代的到来，它现在正在被重新考虑，因为它被认为可以免受使用 Shor 算法的攻击 \[ [here](https://www.tandfonline.com/doi/full/10.1080/23742917.2016.1226650)\]。

NIST 现在已经开始着手研究量子鲁棒方法，并发表了一篇论文，概述了对新密码方法的要求，因为大型量子计算机将破坏当前可用的大多数公钥系统，包括 RSA 和离散对数方法。总体而言，公钥加密最常用于保护对称加密中使用的密钥，并证明身份。大规模泄露公钥将导致对被黑实体在互联网上的完全不信任。

量子鲁棒方法的主要竞争者是：

- **基于格的密码学**——这种分类显示出巨大的潜力，并正在导致新的密码学，例如全同态加密 \[ [here](https://asecuritysite.com/encryption/pal)\] 和代码混淆。以下部分给出了一个例子。
- **基于代码的密码学**——该方法于 1978 年通过 McEliece 密码系统创建，但在实际应用中几乎没有使用。McEliece 方法使用线性码，该线性码用于纠错码，并且涉及矩阵向量乘法。线性码的一个例子是 Hamming 码 \[ [here](https://asecuritysite.com/comms/hamming)\]
- **多元多项式密码学**——这些重点关注在有限域上求解多元多项式系统的难度。不幸的是，许多已提出的方法已被破解。
- **基于哈希的签名**——这将涉及使用哈希方法创建数字签名。缺点是签名者需要跟踪已签名的所有消息，并且可以生成的签名数量有限。

### McEliece 方法

McEliece 方法使用基于代码的密码学。它的基础是基于解码一般线性码的难度，并且通常比用于加密和解密的 RSA 更快。在其中，我们有一种概率密钥生成方法，然后用于生成公钥和私钥。密钥是使用 n、k 和 T 的参数生成的。

密钥是使用参数 n、k 和 t 生成的。有了它，我们创建了一个 \[n,k\] 代码矩阵，它可以纠正 t 个错误。在他的论文中，McEliece 定义了 n=1024、k=524、t=50，这给出了 524x(1024–524) = 262,000 位的公钥大小。在上面的示例中，我们使用 k=1608、N=2048 和 T=40，这给出了 1608x(2048–40) 的公钥大小 - 3,228,864 位。对于量子鲁棒性，建议 N 为 6960，k 为 5,412，t 为 119（给出 8,373,911 位的大密钥大小）。

这是加密的演示 \[ [here](https://asecuritysite.com/pqc/mce)\]。

### 例子

本页提供了一个简单的解释，说明如何为 McEliece 加密创建密钥。它使用具有一位纠错的 (7,4) Hamming 码。以下是一个大纲 \[ [here](https://asecuritysite.com/pqc/mce_k)\]：

```python
import numpy
import sysg =numpy.array([[1,0,0,0,1,1,0],[0,1,0,0,1,0,1],[0,0,1,0,0,1,1 ],[0,0,0,1,1,1,1]])
s =numpy.array([[1,1,0,1],[1,0,0,1],[0,1,1,1],[1,1,0,0]])
p=numpy.array([[0,1,0,0,0,0,0],[0,0,0,1,0,0,0],[0,0,0,0,0,0,1],[1,0,0,0,0,0,0],[0,0,1,0,0,0,0],[0,0,0,0,0,1,0],[0,0,0,0,1,0,0]])print 'G:\n',g
print 'S:\n',s
print 'P:\n',pmatrix = numpy.dot(s,g)%2
G_1 = numpy.dot(matrix,p)%2print 'Result:\n',G_1message = ([1,1,0,1])
e = ([0,0,0,0,1,0,0])res=numpy.dot(message,G_1)%2cipher = numpy.add(res,e)%2print '\nCipher:',cipherp_1=numpy.linalg.inv(p)%2print '\nP^{-1}:\n',p_1y_1 = numpy.dot(cipher,p_1)%2print "\ny':",y_1
```

这是基于示例 \[ [here](http://www-math.ucdenver.edu/~wcherowi/courses/m5410/ctcmcel.html)\]。我们用 (7,4) Hamming 码说明该过程，该码纠正一个错误。然后生成器矩阵为：

```
1  0  0  0  1  1  0
         G = 0  1  0  0  1  0  1
             0  0  1  0  0  1  1
             0  0  0  1  1  1  1
```

然后 Bob 选择一个加扰矩阵 (S)：

```
1  1  0  1
          S = 1  0  0  1
              0  1  1  1
              1  1  0  0
```

以及一个置换矩阵：

```
0  1  0  0  0  0  0
              0  0  0  1  0  0  0
              0  0  0  0  0  0  1
         P =  1  0  0  0  0  0  0
              0  0  1  0  0  0  0
              0  0  0  0  0  1  0
              0  0  0  0  1  0  0
```

然后，Bob 的公钥变为这些矩阵的点积

```
1  1  1  1  0  0  0
     G' = SGP   = 1  1  0  0  1  0  0
                  1  0  0  1  1  0  1
                  0  1  0  1  1  1  0
```

Bob 将使用 G’ 作为公钥，但 S、G 和 P 是秘密的。接下来，对于 Alice 向 Bob 发送加密消息，她将消息转换为长度为 k 的二进制向量。

对于消息 m，Alice 将随机创建一个权重为 t 的二进制 n 向量（并在长度为 n 的零向量中随机放置 t 个 1）。

然后将其发送给 Bob：

y = mG’ + e

然后 Bob 使用以下方式解密：

_yP_ −1=( _mG_′+ _e_) _P_ −1= _mSG_ + _eP_ −1= _mSG_ + _e_′

一个示例运行是：

```
Message:
 [1. 1. 0. 1.]
G:
 [[1 0 0 0 1 1 1]\
 [0 1 0 0 0 1 1]\
 [0 0 1 0 1 0 1]\
 [0 0 0 1 1 1 0]]
S:
 [[1 1 0 1]\
 [1 0 0 1]\
 [0 1 1 1]\
 [1 1 0 0]]
P:
 [[0 1 0 0 0 0 0]\
 [0 0 0 1 0 0 0]\
 [0 0 0 0 0 0 1]\
 [1 0 0 0 0 0 0]\
 [0 0 1 0 0 0 0]\
 [0 0 0 0 0 1 0]\
 [0 0 0 0 1 0 0]]
Result (GSP):
 [[1 1 0 1 0 1 0]\
 [1 1 0 0 1 0 0]\
 [1 0 0 1 0 0 1]\
 [0 1 1 1 0 0 0]]Cipher: [0. 1. 1. 0. 0. 1. 0.]P^{-1}:
 [[0. 0. 0. 1. 0. 0. 0.]\
 [1. 0. 0. 0. 0. 0. 0.]\
 [0. 0. 0. 0. 1. 0. 0.]\
 [0. 1. 0. 0. 0. 0. 0.]\
 [0. 0. 0. 0. 0. 0. 1.]\
 [0. 0. 0. 0. 0. 1. 0.]\
 [0. 0. 1. 0. 0. 0. 0.]]syndrome': [1. 0. 1.] 5.0
Error position:  7
y':  [1. 0. 0. 0. 1. 1. 0.]
y' (corrected):  [1. 0. 0. 0. 1. 1. 1.]S^{-1}:
 [[1. 1. 0. 1.]\
 [1. 1. 0. 0.]\
 [0. 1. 1. 1.]\
 [1. 0. 0. 1.]]Decipher: [1. 1. 0. 1.]
```

## 结论

在量子计算机时代，我们需要考虑定义难题的新方法。使用代数码来创建量子鲁棒密码现在是取代某些公钥方法的有力竞争者。

Robert McEliece 绝对是天才，我们需要更多天才来重建我们有缺陷的互联网。请观看此视频，看看一位伟大的老师如何使事物栩栩如生：

因此，这里是密钥和密文的大小：

```
Type      Public key size (B)   Secret key size (B)  Ciphertext size (B)
------------------------------------------------------------------------
Kyber512              800              1,632                  768  Learning with errors (Lattice)
Kyber738            1,184              2,400                1,088  Learning with errors (Lattice)
Kyber1024           1,568              3,168                1,568  Learning with errors (Lattice)
Bike128             1,541              3,114                1,573  Code-based
Bike192             3,083              6,198                3,115  Code-based
Bike256             5,122             10,276                5,154  Code-based
HQC128              2,249              2,289                4,497  Code-based
HQC192              4,522              4,562                9,042  Code-based
HQC256              7,245              7,285               14,485  Code-based
McEliece348864    261,120              6,492                  196  Code based
McEliece460896    524,160             13,608                  156  Code based
McEliece6688128 1,044,992             13,932                  208  Code based
McEliece6960119 1,047,319             13,948                  194  Code based
McEliece8192128 1,357,824             14,120                  208  Code based
```

为什么不选择 McEliece？

>- 原文链接： [medium.com/asecuritysite...](https://medium.com/asecuritysite-when-bob-met-alice/why-not-pick-mceliece-for-pqc-encryption-0a9c24af23a0)
>- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～

为什么不选择 McEliece 作为 PQC 加密？

但是，在 PQC 加密/密钥封装方面，NIST 只有一个已定义的标准：ML-KEM (Kyber)/FIPS 203。因此，在 2025 年 3 月，它还宣布 HQC 将被标准化，但 HQC 团队宣布 HQC 存在一些设计缺陷 [ here]：

Classic Mceliece

Type      Public key size (B)   Secret key size (B)  Ciphertext size (B)
McEliece348864    261,120              6,492                  196  Code based
McEliece460896    524,160             13,608                  156  Code based
McEliece6688128 1,044,992             13,932                  208  Code based
McEliece6960119 1,047,319             13,948                  194  Code based
McEliece8192128 1,357,824             14,120                  208  Code based

不幸的是，它在密钥生成方面很慢，但提供了可接受的封装和解封装性能：

我们可以实现为 [ here]：

namespace Cmce
{
    using Org.BouncyCastle.Pqc.Crypto.Cmce;
    using Org.BouncyCastle.Security;
    class Program
    {
        static void Main(string[] args)
        {
try {
                var size="mceliece460896r3";
                if (args.Length >0) size=args[0];
                var random = new SecureRandom();
                var keyGenParameters = new   CmceKeyGenerationParameters(random, CmceParameters.mceliece348864r3);
                if (size=="mceliece460896r3") keyGenParameters = new CmceKeyGenerationParameters(random, CmceParameters.mceliece460896r3);
                else if (size=="mceliece6960119r3") keyGenParameters = new CmceKeyGenerationParameters(random, CmceParameters.mceliece6960119r3);
               else if (size=="mceliece6688128r3") keyGenParameters = new CmceKeyGenerationParameters(random, CmceParameters.mceliece6688128r3);
               else if (size=="mceliece8192128r3") keyGenParameters = new CmceKeyGenerationParameters(random, CmceParameters.mceliece8192128r3);
                var CmceKeyPairGenerator = new CmceKeyPairGenerator();
                CmceKeyPairGenerator.Init(keyGenParameters);

                var aKeyPair = CmceKeyPairGenerator.GenerateKeyPair();
                var aPublic = (CmcePublicKeyParameters)aKeyPair.Public;
                var aPrivate = (CmcePrivateKeyParameters)aKeyPair.Private;

                var pubEncoded =aPublic.GetEncoded();
                var privateEncoded = aPrivate.GetEncoded();
                var bobCmceKemGenerator = new CmceKemGenerator(random);
                var encapsulatedSecret = bobCmceKemGenerator.GenerateEncapsulated(aPublic);
                var bobSecret = encapsulatedSecret.GetSecret();
                var cipherText = encapsulatedSecret.GetEncapsulation();
                var aliceKemExtractor = new CmceKemExtractor(aPrivate);
                var aliceSecret = aliceKemExtractor.ExtractSecret(cipherText);
                Console.WriteLine("Cmce-{0}",size);
                Console.WriteLine("Private key length:\t\t{0} bytes",aPrivate.GetEncoded().Length);
                Console.WriteLine("Public key length:\t\t{0} bytes",aPublic.GetEncoded().Length);
                Console.WriteLine("Ciphertext length:\t\t{0} bytes",cipherText.Length);
                Console.WriteLine("\nAlice private (first 50 bytes):\t{0}",Convert.ToHexString(aPrivate.GetEncoded())[..100]);
                Console.WriteLine("Alice public (first 50 bytes):\t{0}",Convert.ToHexString(aPublic.GetEncoded())[..100]);
                Console.WriteLine("\nCipher (first 50 bytes):\t{0}",Convert.ToHexString(cipherText)[..100]);
                Console.WriteLine("\nBob secret:\t\t{0}",Convert.ToHexString(bobSecret));
                Console.WriteLine("Alice secret:\t\t{0}",Convert.ToHexString(aliceSecret));
            } catch (Exception e) {
                Console.WriteLine("Error: {0}",e.Message);
            }
        }
    }
}

以及示例运行 [ here]：

Cmce-mceliece8192128
Private key length:  14120 bytes
Public key length:  1357824 bytes
Ciphertext length:  208 bytes

Alice private (first 50 bytes): 10FCB7ACD5F28BA1371728D4F8A4468E40C88306CF5505B841E984A86F6AF725FFFFFFFF00000000A405F8015B05380E6718
Alice public (first 50 bytes): 81E5EEDA642A34955CF33D5C4FBD9A400862BF4593DF255F5BBBEC9B6EC805861A9946A8B90D2635C812A7DE7B993D9A034E
Cipher (first 50 bytes): 5C911606AFDB30BA16F914364DF2B1949C19A827FF70BC8B64B03AD0F2C9AE53FD1C3A4161EE01632358EF851D00047F334A
Bob secret:  FCBAE584DA20AD5A17827D1BA233331169E9BA11B4369F91F43CBCADD91B128E
Alice secret:  FCBAE584DA20AD5A17827D1BA233331169E9BA11B4369F91F43CBCADD91B128E

这里有更多的例子：

McEliece 公钥加密方法（后量子鲁棒）

Robert J. McEliece

在给任何现代研究人员的一个教训中，罗伯特·麦克利斯 (Robert McEliece) 仅用了两页纸，就在 1978 年概述了一种基于代数编码的公钥加密方法——现在称为 McEliece 密码方法 [ paper]. 它是一种非对称加密方法（具有公钥和私钥），当时看起来是活板门方法的有力竞争者。不幸的是，RSA 成为山丘之王，而 McEliece 方法被推到了设计者的队列末尾。

它基本上漂移了近 40 年。但是，随着量子计算机时代的到来，它现在正在被重新考虑，因为它被认为可以免受使用 Shor 算法的攻击 [ here]。

量子鲁棒方法的主要竞争者是：

基于格的密码学——这种分类显示出巨大的潜力，并正在导致新的密码学，例如全同态加密 [ here] 和代码混淆。以下部分给出了一个例子。
基于代码的密码学——该方法于 1978 年通过 McEliece 密码系统创建，但在实际应用中几乎没有使用。McEliece 方法使用线性码，该线性码用于纠错码，并且涉及矩阵向量乘法。线性码的一个例子是 Hamming 码 [ here]
多元多项式密码学——这些重点关注在有限域上求解多元多项式系统的难度。不幸的是，许多已提出的方法已被破解。
基于哈希的签名——这将涉及使用哈希方法创建数字签名。缺点是签名者需要跟踪已签名的所有消息，并且可以生成的签名数量有限。

McEliece 方法

密钥是使用参数 n、k 和 t 生成的。有了它，我们创建了一个 [n,k] 代码矩阵，它可以纠正 t 个错误。在他的论文中，McEliece 定义了 n=1024、k=524、t=50，这给出了 524x(1024–524) = 262,000 位的公钥大小。在上面的示例中，我们使用 k=1608、N=2048 和 T=40，这给出了 1608x(2048–40) 的公钥大小 - 3,228,864 位。对于量子鲁棒性，建议 N 为 6960，k 为 5,412，t 为 119（给出 8,373,911 位的大密钥大小）。

这是加密的演示 [ here]。

例子

本页提供了一个简单的解释，说明如何为 McEliece 加密创建密钥。它使用具有一位纠错的 (7,4) Hamming 码。以下是一个大纲 [ here]：

import numpy
import sysg =numpy.array([[1,0,0,0,1,1,0],[0,1,0,0,1,0,1],[0,0,1,0,0,1,1 ],[0,0,0,1,1,1,1]])
s =numpy.array([[1,1,0,1],[1,0,0,1],[0,1,1,1],[1,1,0,0]])
p=numpy.array([[0,1,0,0,0,0,0],[0,0,0,1,0,0,0],[0,0,0,0,0,0,1],[1,0,0,0,0,0,0],[0,0,1,0,0,0,0],[0,0,0,0,0,1,0],[0,0,0,0,1,0,0]])print 'G:\n',g
print 'S:\n',s
print 'P:\n',pmatrix = numpy.dot(s,g)%2
G_1 = numpy.dot(matrix,p)%2print 'Result:\n',G_1message = ([1,1,0,1])
e = ([0,0,0,0,1,0,0])res=numpy.dot(message,G_1)%2cipher = numpy.add(res,e)%2print '\nCipher:',cipherp_1=numpy.linalg.inv(p)%2print '\nP^{-1}:\n',p_1y_1 = numpy.dot(cipher,p_1)%2print "\ny':",y_1

这是基于示例 [ here]。我们用 (7,4) Hamming 码说明该过程，该码纠正一个错误。然后生成器矩阵为：

1  0  0  0  1  1  0
         G = 0  1  0  0  1  0  1
             0  0  1  0  0  1  1
             0  0  0  1  1  1  1