在Groth中实现查找表：r的第二个秘密成分……

在 Groth 中实现查找：减少 Bionetta 约束的第二个秘密武器

Rarimo

Illia Dovhopolyi, Artem Sdobnov, Dmytro Zakharov

致谢

这里解释的 UltraGroth 证明系统是最初在 Merlin404 在 HackMD 上的文章 中描述的协议的实际用例改编版本。非常感谢他们的工作，它启发了以下的大部分内容。

前提条件

我们假设你已经了解现代零知识 (ZK) 构造的基础知识。本文旨在围绕 UltraGroth 证明系统建立直觉，而对 Groth16 的深入、正式的了解并非绝对必要。但是，熟悉我们之前关于 Bionetta 框架的博客将是有益的，因为此处的示例使用了 Bionetta 电路。

激活函数太昂贵了

在 Bionetta 的开发过程中，我们面临的最大挑战之一是优化诸如 ReLU 之类的激活函数的约束成本。由于输入信号的位分解，每个 ReLU 操作至少花费 253253253 个约束。考虑到神经网络严重依赖非线性激活，这很快变得非常昂贵。例如，考虑我们的 LeakyReLU 实现：

template LeakyReLUwithCutPrecision(...) {
    signal input inp;
    signal output out;

    var absBits[253] = abs_in_bits(inp);

    signal absInBits[253];

    var abs = 0;
    var pow = 1;
    for (var i = 0; i < 253; i++) {
        absInBits[i] <-- absBits[i];
        // We need to constraint each bit is either 0 or 1 separately :(
        absInBits[i]*(1 - absInBits[i]) === 0;
        abs += pow * absInBits[i];
        pow += pow;
    }
    (abs - inp)*(abs + inp) === 0;

    // 3 more constraints for max(0, inp) and precision cut
}

我们的“zkLiveness”模型用于检测输入照片是否对应于真实的人（而不是来自某人设备的照片），需要 386438643864 个非线性激活，总计至少 3864×253=977592个约束。

最初，降低这里的约束似乎是不可能的——我们无法降低激活计数或简化位检查。进一步的研究表明，PlonKish 证明系统引入了一种突出的解决方案，其中使用查找表验证同一函数的重复计算。

但是，我们坚持使用 Groth16，因为它具有其他 Bionetta 特定的优势，例如“零”约束线性层。为了充分利用两者的优势，我们开发了 UltraGroth——一种基于 Groth 的证明系统，可将查找引入我们的电路😎

高效查找参数

查找表背后的想法很简单。与其单独检查每一位，不如将激活函数输入分成更大的块，并对照预定义的查找表验证它们，该查找表包含从 0 到 2chunk_size−12^\text{chunk\_size} - 12chunk_size−1 的所有值。

为此，让我们首先重写前面示例中的 LeakyReLU 函数，以便它将输入信号分成块并输出它们，以便我们可以稍后检查它们的范围：

template LookupReLU(CHUNK_NEW, CHUNK_OLD, CHUNK_SIZE) {
    assert (CHUNK_NEW <= CHUNK_OLD);

    signal input inp;
    signal output out;

    // Now the ReLU outputs chunks so we can handle range check later
    signal output absInChunks[253 \ CHUNK_SIZE];

    var absChunks[253 \ CHUNK_SIZE];

    for (var i = 0; i < 253 \ CHUNK_SIZE; i++) {
        absChunks[i] = (value >> (i * CHUNK_SIZE)) & ((1 << CHUNK_SIZE) - 1);
    }

    var abs = 0;
    var pow = 1;
    for (var i = 0; i < 253 \ CHUNK_SIZE; i++) {
        // We don't need to constraint each bit anymore
        absInChunks[i] <-- absChunks[i];
        abs += pow * absInChunks[i];
        pow *= 1<<CHUNK_SIZE;
    }
    (abs - inp)*(abs + inp) === 0;

     // 3 more constraints for max(0, inp) and precision cut
}

在顶层电路中，我们将来自具有非线性激活的层的所有块组合成单个信号向量。虽然每个激活都会产生多个块（CHUNK_FOR_NUM），但它们的顺序在这里并不重要：

var CHUNK_SIZE = 15;
var CHUNK_FOR_NUM = 253 / CHUNK_SIZE;
var CHUNK_NUM = /* sum calculated based on network layers */;
var CHUNK_BUSY = 0;
signal chunks[CHUNK_NUM];

// Some layer with non-linearities
component layer1Comp = LookupEDLightConv2D(...);
layer1Comp.inp <== image;

// Aggregating chunks from activation functions
for (var i = 0; i < layer_size * CHUNK_FOR_NUM; i++) {
    chunks[i + CHUNK_BUSY] <== layer1Comp.chunks[i];
}
CHUNK_BUSY += layer_size * CHUNK_FOR_NUM;

要完成此优化，我们必须确保每个聚合块都在预期范围内。此验证通过查找参数完成。

考虑一个查找表 L=(ℓ0,ℓ1,…,ℓn)=(0,1,…,2chunk_size)L = (\ell_0, \ell_1, \ldots,\ell_n) = (0, 1, \dots, 2^{\text{chunk\_size}})L=(ℓ0​,ℓ1​,…,ℓn​)=(0,1,…,2chunk_size)，表示范围 [0; 2chunk_size−1]2^{\text{chunk\_size}} - 1]2chunk_size−1]。我们的目标是证明向量 C=(c0,c1,…,cmC = (c_0, c_1, \ldots, c_mC=(c0​,c1​,…,cm​) 中的每个块 cic_ici​ 都存在于 LLL 中。因此，所有块值都必须在指定范围内。

为了约束这一点，我们首先计算每个值在块中出现的次数，创建一个重数向量 M=(m0,m1,…,mn)M = (m_0, m_1, \ldots, m_n)M=(m0​,m1​,…,mn​)，其中 mim_imi​ 是值 iii 在 CCC 中的出现次数。

最后，使用一个随机挑战点 rand\mathsf{rand}rand，我们执行以下检查：

s1=∑i=0m1rand−ci,s2=∑i=0nmirand−ℓi,s1=?s2s_1 =\sum_{i=0}^{m} \frac{1}{\mathsf{rand} - c_i}, \quad s_2 = \sum_{i=0}^{n} \frac{m_i}{\mathsf{rand} - \ell_i}, \quad s_1 \stackrel{?}{=} s_2s1​=i=0∑m​rand−ci​1​,s2​=i=0∑n​rand−ℓi​mi​​,s1​=?s2​

如果此等式成立，则确认所有块值都在查找表中。详细的推理和证明可在本文中找到。

这是此检查在 Bionetta 电路中的样子：

signal input rand;
signal chunks[CHUNK_NUM];

// Aggregating chunks

// Counting m_i coefficients
var m_temp[1<<CHUNK_SIZE];
for (var i = 0; i < CHUNK_NUM; i++) {
   m_temp[chunks[i]]++;
}

signal m[1<<CHUNK_SIZE];
m <-- m_temp;

var s1 = 0;
var s2 = 0;
signal inv1[CHUNK_NUM];
signal inv2[1<<CHUNK_SIZE];
signal prod[1<<CHUNK_SIZE];

// Counting s1
for (var i = 0; i < CHUNK_NUM; i++) {
   inv1[i] <-- (chunks[i] + rand) != 0 ? 1 / (chunks[i] + rand) : 0;
   inv1[i] * (chunks[i] + rand) === 1;
   s1 += inv1[i];
}

// Counting s2
for (var i = 0; i < 1<<CHUNK_SIZE; i++) {
   inv2[i] <-- (i + rand) != 0 ? 1 / (i + rand) : 0;
   inv2[i] * (i + rand) === 1;
   prod[i] <== inv2[i] * m[i];
   s2 += prod[i];
}

s1 === s2;

为什么选择 UltraGroth？

上面介绍的查找参数取决于单个字段元素 rand\text{rand}rand。如果证明者可以自由选择 rand\text{rand}rand，则他可能会恶意选择一个值，该值使得 ∑i=0m1rand−ci=?∑i=0nmirand−li\sum_{i=0}^{m} \frac{1}{\text{rand} - c_i} \stackrel{?}{=} \sum_{i=0}^{n} \frac{m_i}{\text{rand} - l_i}∑i=0m​rand−ci​1​=?∑i=0n​rand−li​mi​​ 成立，即使某些块 cic_ici​ 不在表 LLL 中。

UltraGroth 通过从先前提交的见证部分派生挑战来防止这种情况。我们将私有见证分成两轮：

在证明者计算出第一个承诺 C1C_1C1​ 之后，验证者会派生 rand=Hash(C1)\text{rand} = \text{Hash}(C_1)rand=Hash(C1​)。

在 Groth16 中，验证者使用单个配对等式检查证明：

e(A,B)=e([α]1,[β]2)⋅e(C,[δ]2)⋅e(IC,[γ]2)e(A, B) = e([\alpha]_1, [\beta]_2) \cdot e(C, [\delta]_2) \cdot e(IC, [\gamma]_2)e(A,B)=e([α]1​,[β]2​)⋅e(C,[δ]2​)⋅e(IC,[γ]2​)

在 UltraGroth 中，此等式略有变化。证明者不是发送单个承诺 CCC，而是发送两个承诺：C1C_1C1​ 和 C2C_2C2​。验证者更新配对检查为：

e(A,B)=e([α]1,[β]2)⋅e(C1,[δ1]2)⋅e(C2,[δ2]2)⋅e(IC,[γ]2)e(A, B) = e([\alpha]_1, [\beta]_2) \cdot e(C_1, [\delta_1]_2) \cdot e(C_2, [\delta_2]_2) \cdot e(IC, [\gamma]_2)e(A,B)=e([α]1​,[β]2​)⋅e(C1​,[δ1​]2​)⋅e(C2​,[δ2​]2​)⋅e(IC,[γ]2​)

此外，验证者不接受来自证明者的随机值。相反，它自己派生随机性：rand=Hash(C1)\text{rand}=\text{Hash}(C_1)rand=Hash(C1​)。然后将此派生值插入到公共输入承诺（即 ICICIC）中，以便它是最终验证检查的一部分。

为了使该方案实用，我们修改了最快的开源 Groth16 堆栈，而不是从头开始。

• https://github.com/rarimo/ultragroth — UltraGroth 证明者（https://github.com/iden3/rapidsnark 的分支）。

• https://github.com/rarimo/ultragroth-snarkjs — UltraGroth zkey 和 Solidity 验证器生成器（https://github.com/iden3/snarkjs 的分支）。

请注意，UltraGroth 与 Groth16 的 powers-of-tau 兼容，因此你不需要新的可信设置。

这节省了多少约束？

让我们估算一下节省量。假设模型有 n=3864n = 3864n=3864 个激活，每个激活都有一个 b=253b = 253b=253 位输入。与其单独检查每一位，不如将输入分成大小为 ℓ=15\ell = 15ℓ=15 位的块。

在原始方法中，每个激活都需要 bbb 个约束来执行完整的位分解。因此，约束的总数仅为 n×b=3864×353=977592n \times b = 3864 \times 353 = \color{blue}{977592}n×b=3864×353=977592 个约束。

在基于查找的方法中，约束成本来自两个部分。首先，我们需要 2×2ℓ2 \times 2^{\ell}2×2ℓ 个约束来处理查找表逆和。其次，我们将每个激活分成 ⌊b/ℓ⌋\lfloor b / \ell \rfloor⌊b/ℓ⌋ 个块，从而为块逆和产生额外的 n×⌊b/ℓ⌋n \times \lfloor b / \ell \rfloorn×⌊b/ℓ⌋ 个约束。总而言之，新的总约束数为：

2×2ℓ+n×⌊b/ℓ⌋=2×215+3864×⌊253/15⌋=65536+61824=1273602 \times 2^{\ell} + n \times \lfloor b / \ell \rfloor = 2×2^{15}+3864× \lfloor 253/15 \rfloor =65536+61824=\color{green}{127360}2×2ℓ+n×⌊b/ℓ⌋=2×215+3864×⌊253/15⌋=65536+61824=127360

因此，我们从 $\color{blue}{977592} $ 下降到 127360\color{green}{127360}127360 个约束。这使我们获得了超过 7×7 \times7× 的改进，对于更重的电路来说，改进甚至更多。

图 1 显示了应用查找优化前后的约束数量：红色图表示原始 Groth16 成本随激活数量线性增加，而蓝色和绿色图分别对应于 14 和 15 的块大小。请注意，即使激活从 15000 增加到 30000，这两个优化图都保持在图表底部附近，仅略有增长。

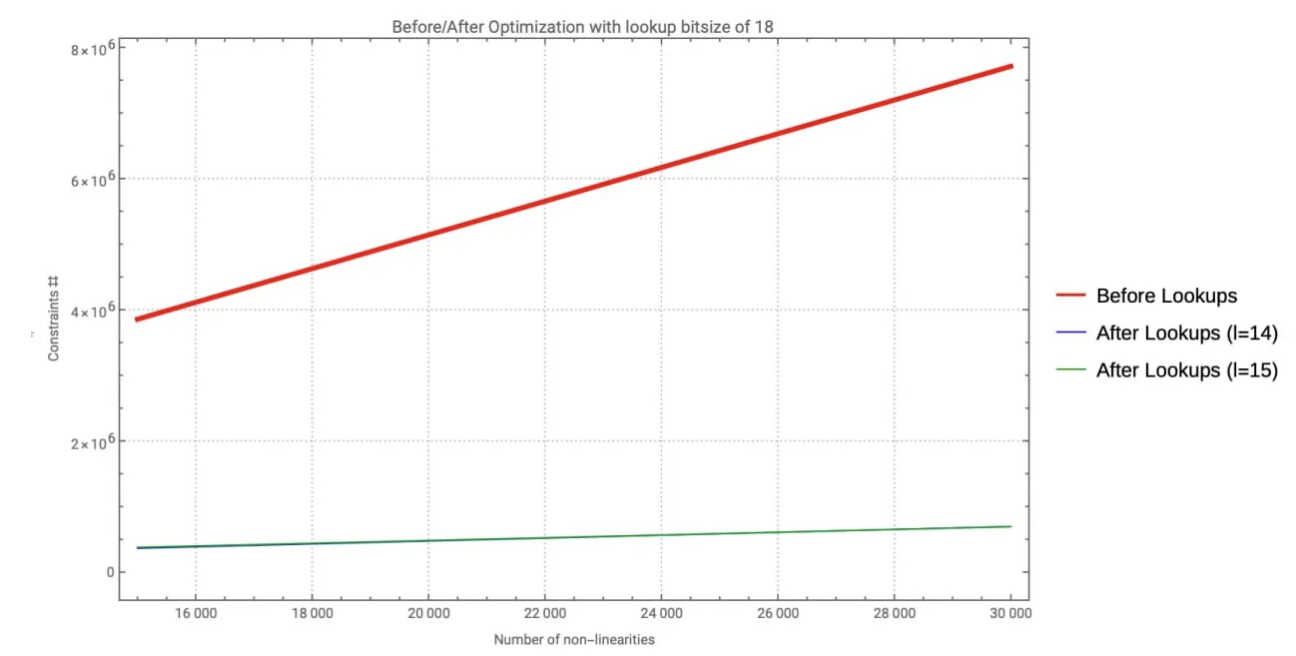
应用查找优化前后的约束数量。

UltraGroth 基准测试

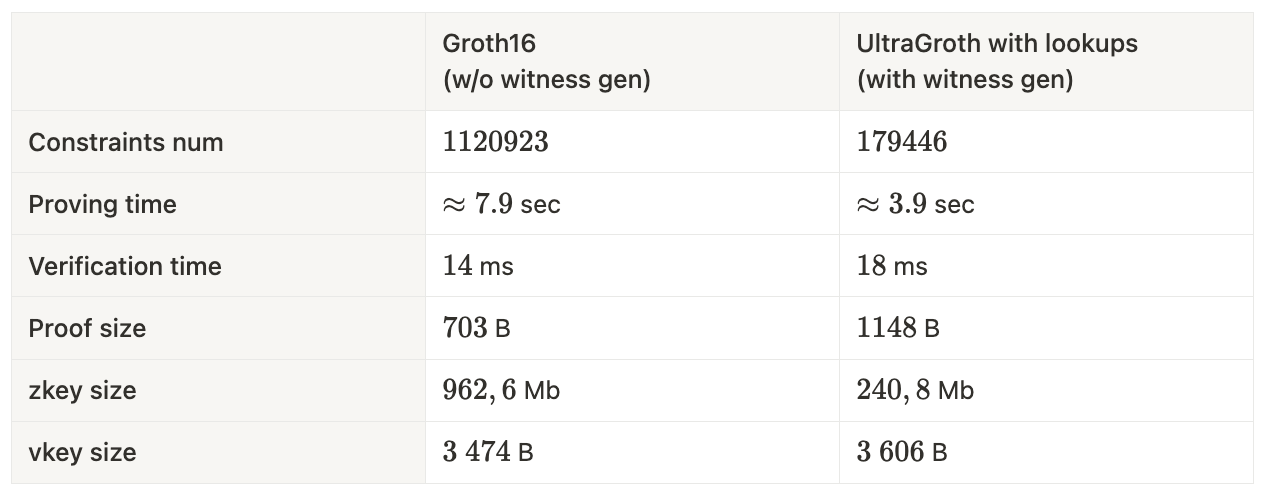
• 原文链接： mirror.xyz/0x90699B5A52B...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～