Goblin Plonk: 惰性递归证明组合

简介

• [High level overview(高级别概述)](/GfNR5SE5ShyXXmLxNCsg3g)
• [Recursion protocol(递归协议)](/dUsu57SOTBiQ4tS9KJMkMQ)

章节

• [Speeding up SNARKs with an Instruction Machine(使用指令机器加速SNARK)](/kMfIhwzNQ_WAa78lqfhkUA)
• [Aggregating Instruction Machine transcripts(聚合指令机器转录)](/03EZcIU1Riq7t-H1uqwNVw)
• [Processing IM Transcripts + curve transposition(处理IM转录+曲线转置)](/wwNI75vmSrSMqcIDznlzxQ)
• [Non-Native Field Virtual Machine(非原生域虚拟机)](/PJWE1lpSQqaWKQbYajwf1g)
• [Elliptic Curve Virtual Machine(椭圆曲线虚拟机)](/fWAdULyqTiyCSjuCmCxHwA))

Recursion Protocol(递归协议)

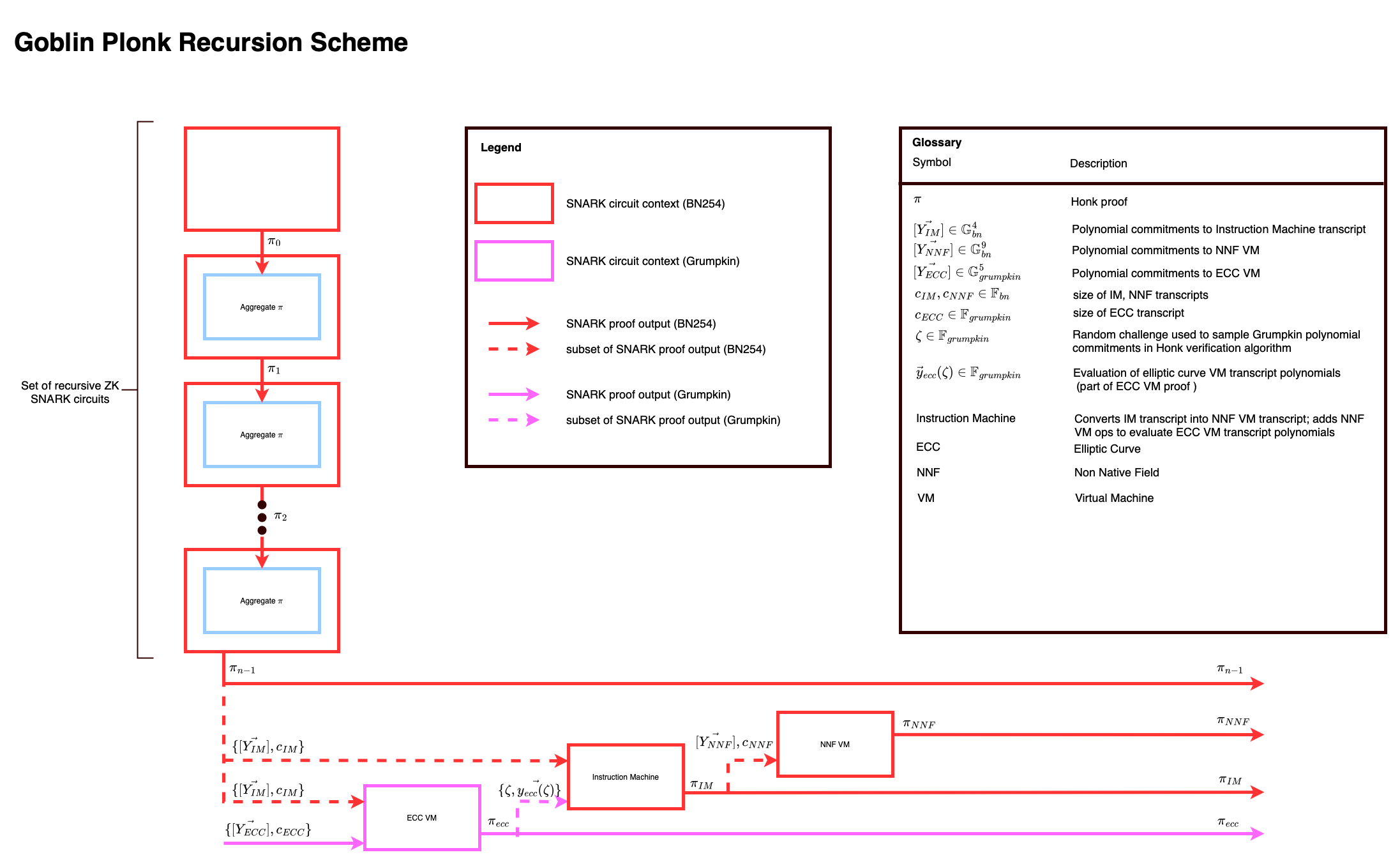
https://hackmd.io/_uploads/B1Z__PLxh.png 上的更大图像

Recursive proof composition steps(递归证明组合步骤)

目标是证明 BN254 转录承诺 \([Y_1]_{IM}, [Y_2]_{IM}, [Y_3]_{IM}, [Y_4]_{IM}\) 的正确性。该转录包含“椭圆曲线虚拟机”的指令，以执行 BN254 群组操作，这些操作是验证递归证明堆栈中中间证明所必需的。

1. 递归聚合器电路从指令机器转录中查找非原生群组操作
2. 递归聚合器电路有效地将指令机器转录承诺聚合到转录累加器 \([Y_1]_{IM}, [Y_2]_{IM}, [Y_3]_{IM}, [Y_4]_{IM}\) 中
3. 为椭圆曲线 VM（基于 Grumpkin 曲线）生成转录承诺
4. 计算椭圆曲线 VM（基于 Grumpkin 曲线）的证明。此证明包含在挑战值 \(\zeta\) 处对 Grumpkin 转录多项式的评估
5. 使用曲线转置电路执行以下操作：
   1. 从 BN254 转录中推导出椭圆曲线 VM 转录系数
   2. 将椭圆曲线 VM 转录系数转换为非原生域VM 指令，t 在 \(\zeta\) 处评估椭圆曲线 VM 转录多项式（并断言它们等效于 Grumpkin 评估）
6. 计算非原生域 VM（基于 BN254 曲线）的证明

注意：

如果假设成熟的 Honk 协议出于其他目的使用非原生域 VM（例如，secp256k1 签名，EIP4844 blobs），那么使用非原生域 VM 评估椭圆曲线 VM 转录多项式在证明者方面是高效的。（相对于在曲线转置电路中进行非原生域算术运算）

Protocol(协议)

TODO: 标准 SNARK 定义（证明关系、\(crs\) 的定义、输入字符串、witness(证人)、群组定义、域定义等）。

• \(\mathbb{F}_{BN254}\) = 素数域，其特征等于 BN254 群组阶数
• \(\mathbb{F}_{Grumpkin}\) = 素数域，其特征等于 Grumpkin 群组阶数
• \(\mathbb{G}_{BN254}\) = BN254 \(\mathbb{G}_1\) 群组
• \(\mathbb{G}_{Grumpkin}\) = Grumpkin \(\mathbb{G}_1\) 群组

Elliptic Curve VM Circuit(椭圆曲线 VM 电路)

ECC VM 电路接收包含 \(\{ [\vec{Y}_{ecc}], c_{ecc} \}\) 的输入字符串 \(u_{ECC}\)，其中 \([\vec{Y}_{ecc}] \in \mathbb{G}_{grumpkin}^5, c_{ecc} \in \mathbb{F}_{grumpkin}\)。（即，该电路使用 5 列来描述 VM 指令）。

ECC VM 电路采用 witness(证人) \(w_{ECC}\)，其中包含向量集 \(\{ \vec{y}_{ecc, 0}, ..., \vec{y}_{ecc, 4}\} \in \mathbb{F}_{grumpkin}^{5c_{ecc}}\)

ECC VM 电路的关系验证以下内容：

1. \([\vec{Y}_{ecc}] = \text{ Commit}(\vec{y}_{ecc, 0}, \ldots, \vec{y}_{ecc, 4})\)
2. \(\{ \vec{y}_{ecc, 0}, \ldots, \vec{y}_{ecc, 4} \}\) 描述了一组在 BN254 曲线上的已满足的椭圆曲线运算

可用的椭圆曲线运算由 ECC VM 的指令集定义。

我们要求 ECC VM 电路的证明 \(\pi_{ECC}\) 包含挑战参数 \(\zeta \in \mathbb{F}_{grumpkin}\)。

输入字符串还包含指令机器转录的承诺 \([\vec{Y}_{IM}]\)，以确保 \(\zeta\) 在证明者承诺 \([\vec{Y}_{IM}]\) 之后生成。

向量 \(\vec{Z}\) 定义了 \(\zeta\) 的幂集：\(\{ 1, \zeta, \ldots, \zeta^{c_{ECC} - 1} \} \in \mathbb{F}_{grumpkin}^{c_{ECC}}\)

我们要求 \(\pi_{ECC}\) 包含参数 \(\{ z_0, \ldots, z_4 \} \in \mathbb{F}_{grumpkin}^5\)，它们表示 ECC 转录向量和 \(\vec{Z}\) 的内积。即

\[z_j = \vec{y}_{ECC, j} \circ \vec{Z} \text{ for } j \in [0, \ldots, 4]\]

（假设系数基中的单变量多项式承诺方案，我们将这些内积作为主 SNARK 协议的一部分获得）。

Non-Native Field VM Circuit(非原生域 VM 电路)

NNF VM 电路采用包含 \([\vec{Y}_{NNF}], c_{NNF}\) 的输入字符串 \(u_{NNF}\)，其中 \(\vec{[Y]}_{NNF} \in \mathbb{G}_{BN254}^9\)。（即，VM 电路使用 9 列来描述 VM 指令）

NNF VM 电路采用 witness(证人) \(w_{NNF}\)，其中包含向量集 \(\{ \vec{y}_{NNF, 0}, ..., \vec{y}_{NNF, 8 \} } \in \mathbb{F}_{BN254}^{9c_{NNF}}\)

NNF VM 电路的关系验证以下内容：

1. \([\vec{Y}_{NNF}] = \text{ Commit}(\vec{y}_{NNF})\)
2. \(\vec{y}_{NNF}\) 描述了一组已满足的非原生域运算

可用的非原生域运算由 Non-native field VM(非原生域虚拟机) 的指令集定义。

Instruction Machine Circuit(指令机器电路)

指令机器采用包含以下内容的输入字符串 \(u_{IM}\)：

• \([\vec{Y}_{IM}] \in \mathbb{G}_{BN254}^4\)
• \([\vec{Y}_{NNF}] \in \mathbb{G}_{BN254}^9\)
• \(\zeta \in \mathbb{F}_{grumpkin}\)
• \(\{ z_0, \ldots, z_8 \} \in \mathbb{F}_{grumpkin}\)

witness(证人)字符串 \(w_{IM}\) 包含描述一组输入指令的向量：

• \(\{ \vec{y}_{IM, 0}, \ldots, \vec{y}_{IM, 3} \} \in \mathbb{F}_{BN254}^4\)

其中 \([\vec{Y}_{IM}] = \text{Commit}(\vec{y}_{IM, 0}, \ldots, \vec{y}_{IM, 3})\)

指令机器电路定义了两个映射：\(\sigma_{NNF}, \sigma_{ECC}\)。

\(\sigma_{ECC}\) 映射描述了如何将输入转录 \(\{ \vec{y}_{IM,0}, \ldots, \vec{y}_{IM, 3} \} \in \mathbb{F}_{BN254}^{4c_{IM}}\) 中的椭圆曲线指令转换为 ECC VM 的转录 \(\{ \vec{y}_{ECC, 0}, \ldots, \vec{y}_{ECC, 4} \} \in \mathbb{F}_{grumpkin}^{5c_{ECC}}\) (例如

\[\sigma_{ECC}(\vec{y}_{IM, 0}, \ldots, \vec{y}_{IM, 3}) \rightarrow \{ \vec{y}_{ECC, 0}, \ldots, \vec{y}_{ECC, 4} \} \in \mathbb{F}_{grumpkin}^{5 c_{ecc}}\]

注意：出于效率目的，这些转录的结构不同。IM 转录以 width-4 UltraPlonk 类型的算术化有效地表示指令。ECC 转录以最适合 ECC VM 的方式表示指令。两个转录中的信息相同，但该信息在列/行中的表示形式不同。

\(\sigma_{NNF}\) 映射将输入转录 \(\vec{y}_{IM}\) 转换为 NNF VM 的转录 \(\vec{y}_{NNF}\)：

\[\sigma_{NNF}(\vec{y}_{IM, 0}, \ldots, \vec{y}_{IM, 3}) \rightarrow \{ \vec{y}_{NNF, 0}, \ldots, \vec{y}_{NNF, 8} \} \in \mathbb{F}_{BN254}^{9 c_{NNF}}\]

向量 \(\vec{Z}\) 定义了 \(\zeta\) 的幂集 \(\{ 1, \zeta, \ldots, \zeta^{c_{ECC} - 1} \}\)

编码到 NNF VM 转录中的指令验证了 \(\vec{Z}\) 与从 \(\sigma_{ECC}\) 生成的每个向量的内积等于 \(\{ z_0, \ldots, z_4 \}\)：

\[z_j = \vec{y}_{ECC, j} \circ \vec{Z} \text{ for } j \in [0, \ldots, 4]\]

换句话说，IM 电路生成一个非原生域 VM 转录，该转录验证了内积的正确性：

\[z_j = \sigma_{ECC}(\vec{y}_{IM, 0}, \ldots, \vec{y}_{IM, 3})_j \circ \vec{Z} \text{ for } j \in [0, \ldots, 4]\]

Validating Non-native elliptic curve operations using cycle curves(使用循环曲线验证非原生椭圆曲线运算)

考虑我们有 3 个证明 \(\pi_{ECC}, \pi_{IM}, \pi_{NNF}\) 并且以下情况为真：

1. \(\text{Verify}(crs, u_{ECC}, \pi_{ECC}) = 1\).
2. \(\text{Verify}(crs, u_{IM}, \pi_{IM}) = 1\).
3. \(\text{Verify}(crs, u_{NNF}, \pi_{NNF}) = 1\).
4. \([\vec{Y}_{IM}, c_{IM}] \in u_{ECC}\)
5. \([\vec{Y}_{NNF}, \vec{Y}_{IM}, c_{NNF}, c_{IM}] \in u_{IM}\)
6. \([\vec{Y}_{NNF}, c_{NNF}] \in u_{NNF}\)
7. \(\{ \zeta, z_0, \ldots, z_4 \} \in \pi_{ECC}\)
8. \(\{ \zeta, z_0, \ldots, z_4 \} \in u_{IM}\)

如果满足上述条件，我们可以推断出以下关系成立：

\[\ [\vec{Y}_{IM}] = Commit_{BN254}(\vec{y}_{IM, 0}, \ldots, \vec{y}_{IM, 3}) \\ [\vec{Y}_{ecc}] = Commit_{Grumpkin}(\sigma_{ecc}(\vec{y}_{IM, 0}, \ldots, \vec{y}_{IM, 3}))\ \]

由此我们可以推断出 \(\vec{Y}_{IM}\) 中存在的 bn254 椭圆曲线指令（以及相关的约束和断言）已得到满足。

Goblin-aggregatable SNARKs(Goblin 可聚合的 SNARK)

对于可以使用 goblin 方案聚合的 SNARK，其语句 \(u\) 将包含 \([\vec{Y}_{old}], [\vec{Y}_{new}]\)；在先前的递归步骤和当前的递归步骤中，对指令机器转录进行绑定承诺；即，可以由指令机器协议评估的指令集。这些指令以 \(\vec{y}_{old}, \vec{y}_{new}\) 的形式存在于 witness(证人)中。

承诺 \(\vec{Y_{old}}\) 表示要执行的现有指令集，该指令集独立于当前 SNARK 的电路描述。

承诺 \(\vec{Y_{new}}\) 表示 \(\vec{Y_{old}}\) 中的指令集与当前 SNARK 电路添加到 IM 转录中的指令集的并集。

goblin 方案要求 SNARK 的证明关系证明 \(\vec{Y_{new}}\) 具有正确的结构，并且可以归纳地推断出 \(\vec{Y_{old}}\) 也具有正确的结构。

goblin 方案还要求每个 SNARK 的证明关系都包含_公共聚合方案_ (public aggregation scheme)（例如 Halo2），其中非原生群组运算被委派给 IM。该方案的性质本质上与 Goblin 无关。在 bn254 曲线的情况下，“聚合方案”直接验证证明（将 \(\mathbb{G}_{BN254}\) 运算委派给 IM），但不包括配对。配对检查使用民间聚合方案推迟。

即，考虑两个证明 \(\pi_1, \pi_2\)。递归聚合步骤验证证明，直到必须满足以下配对的点：

\[\ e([A_1], [1]) \cdot e([B_1], [H]) \text{ for } \pi_1 \\ e([A_2], [1]) \cdot e([B_2], [H]) \text{ for } \pi_2\ \]

（其中 \([H]\) 等于 \(x \cdot [1]\)，对于由可信设置生成的某个未知值 \(x\)）。

聚合步骤包括生成随机挑战 \(k\) 并返回聚合点 \(\{ [A_1] + k \cdot [A_2], [B_1] + k \cdot [B_2] \}\)。

• 原文链接： hackmd.io/@aztec-network...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～