基于RLNC的替代DAS概念

基于 RLNC 的替代 DAS 概念

摘要

目前 Ethereum 的 DAS 方法基于 Reed-Solomon 纠删码 + KZG 承诺。这个新的方案（由 @potuz 在 以太坊中更快的区块/blob 传播 中描述）引入了另一对：RLNC (随机线性网络编码) 纠删码 + Pedersen 承诺。它具有一些很好的特性，可以用来开发一种替代的数据可用性方法，并具有其优缺点。

在这篇文档中，我们将描述这种方法的概念——它的好处和挑战。参考算法并不是一个最终的解决方案，可能只是强调了研究替代数据可用性方法的潜在方向。

我们将从最简单的想法开始，然后逐步解决它们的局限性。下面的推理可能有点不成体系或混乱，但它可以帮助澄清实现的基本思想。你可以随意跳过它，直接转到 最终算法描述。

介绍

与文章 以太坊中更快的区块/blob 传播 类似，原始数据被分成 N 个向量

v1,…,vN 在域

Fp 上。 这些向量可以使用 RLNC 进行编码，并通过包含在区块中的 Pedersen 承诺（大小为

32×N）进行承诺。 任何线性组合都可以根据承诺及其相关系数进行验证。

我们还假设这些 系数 可能来自一个更小的子域

Cq，其大小可能小到一个字节——甚至是一位。

让我们也引入 分片因子 S：任何常规节点都需要下载和保管 原始数据 大小的 1/S。

想法 #1

让我们假设我们有足够的“超级节点”（接收和存储所有 N 个块）来服务所有其他 [常规] 节点。

然后，常规节点通过执行以下操作来进行采样 和 保管：

• 在本地选择 N 个随机系数

A=[a1,...,aN]

• 向超级节点请求一个向量，该向量是所有原始数据向量的线性组合：

wA=a1∗v1+...+aN∗vN

• 验证接收到的向量

WA，以针对相应区块的 Pedersen 承诺及其随机系数

以上过程的主要收获：

• 采样节点 [几乎] 可以肯定响应的超级节点拥有 所有数据（该过程的采样端）
• 该节点已经获得并存储了该向量，该向量几乎可以肯定与任何其他诚实节点保管的向量 非共线（该过程的保管端）
  • （派生声明）任何 N 个诚实节点集都足以恢复原始数据

如果所有超级节点都是恶意的，他们所能造成的最大危害是欺骗 N - 1 个节点，使他们将不可用的数据视为可用。

这里我们有 S == N，并且任何常规节点仅下载和保管原始数据大小的 1/S

挑战 1：网络需要有足够的超级节点来服务常规节点。网络不是同质的——有“服务器”和“客户端”。没有 p2p 数据传播。

想法 #2

作为中间步骤，现在让我们拥有一组特定的节点（我们称之为“种子节点”），它们保管自己的原始向量子集，而不是超级节点。假设每个这样的节点只存储 K（K < N）个原始向量：

[v1,...,vK],

[vK+1,...,v2K], 等等。

现在，常规节点需要查询至少 N/K 个种子节点，以确保整个数据被它们集体拥有。

采样后，节点可以将接收到的向量聚合为单个向量（只是具有随机系数的线性组合）并将其存储在保管中。

到目前为止，我们仍然有 S == N

挑战 2：网络中仍然有不同类型的节点

挑战 3：虽然常规节点可能只保管单个向量，但它仍然需要下载原始数据大小的 K/N，而不是现在的 1/N

想法 #3

让我们首先解决 挑战 3：为此，让我们增加原始块的数量。让 S 保持不变，现在让 N = S * K。因此，常规节点现在再次只需要下载原始数据的 1/S

想法 #4

现在让我们尝试解决 挑战 2

现在让“种子”节点存储 K 个原始向量的随机线性组合（

w1,...,wK)，而不是 K 个原始向量：

w1=a1,1∗v1+...+a1,N∗vN

…

wK=aK,0∗v1+...+aK,N∗vN

并让采样节点使用本地随机系数，向其“种子”对等方请求

wi 的线性组合

C=[c1,...,cK]:

wC=c1∗w1+...+cK∗wK

种子对等方需要回复

wC 以及系数

ai,j

在一个节点请求 K 个样本后，它就变成了“种子”节点，并且可以为其他节点请求提供服务。因此，这里我们获得了一个规范的 p2p 网络结构，所有节点都扮演着相同的客户端/服务器角色

但是，这里存在新的挑战：

挑战 4：种子对等方可能拥有的向量比声明的少（它甚至可能只有一个向量），并恶意地制作系数

ai,j

攻击示例：

假设我们有

F256,

C16，数据向量只有一个元素，并且 S = 2（因此 N = 4）

假设原始向量（数据向量只有一个

F256 元素）：

(v1,...,v4)=([32],[55],[1],[255])

诚实的节点应该有 2 个线性组合，但是假设一个恶意节点只有一个带有系数的线性组合：

a1=[a1,1,...,a1,4]=[1,3,7,15]

因此

w1=[32]∗1+[55]∗3+[1]∗7+[255]∗15=[189]

w2 丢失

例如，采样节点请求具有以下系数的组合

C：

C=[c1,c2]=[15,3]

wC=15∗w1′+3∗w2′

采样节点还不知道响应者有哪些线性组合（

w1′ 和

w2′）。它希望从响应中找出答案。

恶意节点用它拥有的唯一向量响应：

wC=w1=[189]，但是声称这是具有以下系数的向量的线性组合：

a1′=[1,1,1,1]/15=[15,15,15,15]

a2′=[0,2,6,14]/3=[0,6,2,10]

15∗a1′+3∗a2′=[1,3,7,15]=a1

wC 是合法的，可以针对

15∗a1′+3∗a2′ 进行验证，

a1′ 和

a2′ 是线性独立的，因此响应是正确的。

想法 #5a

让我们尝试解决 挑战 4

将请求分为 2 个交互：

1. 请求

ai,j 现有向量的系数

2. 用本地随机系数请求这些向量的线性组合

ci

由于现有向量在请求 (1) 之后现在是固定的，因此种子对等方不再可能作弊，并且需要拥有声明的向量（或同一子空间的另一个基）才能计算

wC 以响应请求 (2)

示例：

继续执行先前主题中的示例：如果采样节点首先请求现有

ai，例如，恶意节点响应相同的

[a1′,a2′] 系数。

在这种情况下，只有当请求者请求

C=[15,3]∗k 对于任何

k 时，响应者才能够提供正确的答案。否则它将无法正确响应。

想法 #5b

上述方法解决了 挑战 4，但增加了另一个交互步骤，这在时间紧迫的数据传播期间可能非常重要。

基本上 K 个向量

ai=[ai,1,...,ai,N] 描述了 N 维空间中的 K 维子空间。（我们的节点只需要从这个子空间中采样一个随机选择的向量）。有几乎无限的基向量集来描述同一个子空间，但是如果只有一些单一的规范基来描述这个子空间呢？

我认为矩阵

a 的 简化行阶梯形式 (RREF)

a′ 可能可以用作上述子空间的规范基：

a=[a0,...,aK]

a′=rref(a)

a′=[a1′,...,aK′]

ai′=[ai,1′,...,ai,N′]

然后种子节点可以导出以下数据向量

wi′=ai,1′∗v1+...+ai,N′∗vN

并使用以下的线性组合响应请求：

wC′=c1∗w1′+...+cK∗wK′

由于规范基是隐式唯一的和固定的，这应该使为修复现有系数而进行的额外初步交互变得过时

示例：

继续执行先前主题中的示例…

因此，请求节点现在对系数向量有额外的要求

a1′ 和

a2′：矩阵

[a1′a2′] 应该采用 RREF 形式。

诀窍是，虽然攻击者可以制作任意数量的

(a1′,a2′)，这些值满足

15∗a1′+3∗a2′=a1，但是它不能制作出这样的对以极高的概率成为 RREF 矩阵。

免责声明：最后的陈述非常直观，需要更好的理由。

作为对手，让我们尝试在只有一个向量

w1=[189] 和系数

a1=[1,3,7,15] 的情况下计算 RREF 形式的矩阵

我们现在有 2 个用于恶意制作的系数的边界条件

a1′,

a2′：

1. 应该满足

15∗a1′+3∗a2′=[1,3,7,15]， 因此如果

a1′=[x1,x2,x3,x4], 那么

a2′=[1−15x13,3−15x23,7−15x33,15−15x13]

2. 矩阵

[a1′a2′] 应该采用 RREF 形式，因此具有以下形式（在可能的列置换之后）：

[10y1y201y3y4]

因此我们有这个无解的方程组：

[1001]=[x1x21−15x133−15x23]=>{x1=1x2=01−15x13=03−15x23=1

想法 #6

我们可以在不牺牲安全性的情况下删除剩余的交互。拥有可以从节点的 nodeID 导出的静态公共随机系数，可能很好。在这种情况下，种子节点可以在收到足够的自己的向量后立即组成一个样本向量并将其传播给其对等方。

想法 #7

到目前为止，我们有：

• S - 分片因子
• N - 原始向量的总数
• K = N / S - 节点需要下载和保管的向量数

我们希望最小化 N 以减少承诺和证明开销。

我们希望最大化 S 从而可能获得更好的分片效果

因此，我们要最小化 K。

但是，每个常规节点仅存储 1/S 的数据，并且要采样整个 N 维空间，节点需要下载至少 S 个向量。

因此，K 需要至少与 S 一样大，因此它需要等于 S：

S == K
N = S ^ 2 == K ^ 2

想法 #8

假设子域

Cq 非常小，例如仅适合 1 个字节。然后，对于 S = 32，采样消息应包含 32 * 1024 个系数，即 32 KB，这与数据向量本身的大小相同。听起来像是一个很大的开销。

但是，如果我们使子域

Cq 更小：只有 1 位。从 32 个原始向量中采样的向量仍然很有可能与从相同的 32 个原始向量中采样的另一个随机向量共线 - 1 / 2^32。这并不是微不足道的，但是我们在这里可以接受罕见的冲突。使用 1 位系数，我们只需要 4 KB 即可传递原始系数。这看起来是一个不错的节省。

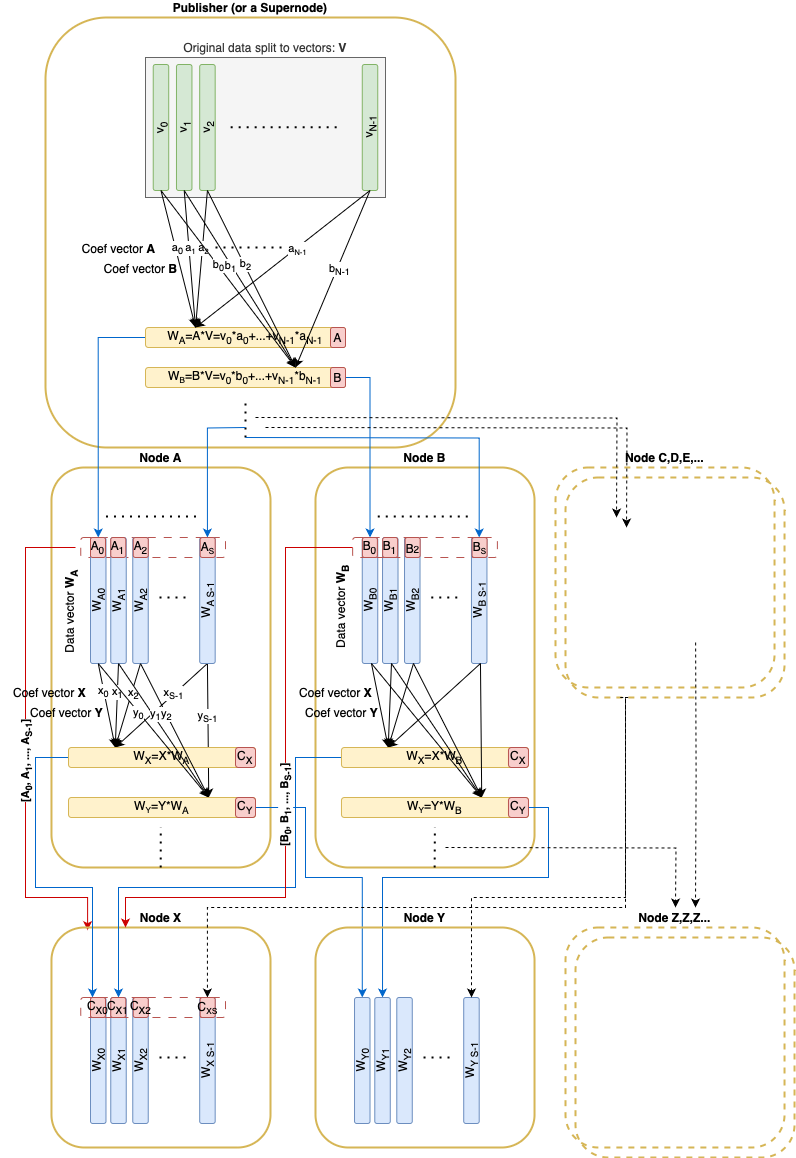
最终算法

简要概述

节点从其对等方接收伪随机线性组合向量。

每个向量都伴随着从中随机采样的子空间的基向量。可以证明子空间基向量存在于对等保管中。

节点进行采样直到

• 所有接收到的基向量加起来构成完整的 N 维空间
• 接收至少 S 个向量以进行保管

之后，节点完成采样并成为“活动”节点，可供其他节点用于采样。

注意事项

下面的类似 Python 的代码段仅用于进行说明，目前不打算对其进行编译和执行。一些显而易见的或类似库的函数目前缺少实现。

类型

令数据向量元素来自有限域

Fp，它可以映射到 32 字节（为了简单起见，是精确的，实际上略低）

def FScalar

令系数来自一个明显较小的子域

Cq 并且可以使用 COEF_SIZE 字节（可以是小数）进行编码

def CScalar

令单个数据向量具有来自

Fp 的 VECTOR_LEN 个元素

def DataVector = Vector[FScalar, VECTOR_LEN]

分片因子 S 表示每个常规节点仅接收、发送和存储整体数据的 1/S 部分。

令 N = S * S 并且令整体数据被分解为 N 个 原始 DataVector：

def OriginalData = Vector[DataVector, N]

派生 DataVector 是 原始 DataVector 的线性组合。由于原始向量只是派生向量的一种特殊情况，因此我们将不再对它们进行任何区分。

要针对承诺验证 DataVector，必须知道其线性组合系数：

def ProofVector = Vector[CScalar, N]

还有稍微不同的系数序列，该系数用于从现有的 DataVector 派生新向量：

def CombineVector = List[CScalar]

结构

伴随有其线性组合系数的数据向量

class DataAndProof:
    data_vector: DataVector
    proof: ProofVector

用于传播的唯一消息是

class DaMessage:
    data_vector: DataVector
    # coefVector for validation is derived
    orig_coeff_vectors: List[CombineVector, N]
    seq_no: Int

存在用于某个区块数据的临时存储：

class BlockDaStore:
    custody: List[DataAndProof, N]
    sample_matrix: List[ProofVector]

    # commitment is initialized first from the corresponding block
    commitment: Vector[RistrettoPoint]

函数

令函数 random_coef 使用种子 (nodeId, seq_no) 生成确定性随机系数向量：

def random_coef(node_id: UInt256, length: int, seq_no: int) -> CombineVector

让我们定义一个抽象的实用程序函数来计算任何向量的线性组合：

def linear_combination(
        vectors: Sequence[AnyVector],
        coefficients: CombineVector) -> AnyVector

该函数同时对 DataVector 和 ProofVector 执行线性运算，以将 ProofVector 转换为 RREF：

def to_rref(data_vectors: Sequence[DataAndProof]) -> Sequence[DataAndProof]
def is_rref(proofs: Sequence[ProofVector]) -> bool

该函数从现有保管向量为特定对等方创建一个新的确定性随机消息：

def create_da_message(
        da_store: BlockDaStore
        receiver_node_id: uint256,
        seq_no: int) -> DaMessage:
    rref_custody_data = to_rref_form(da_store.custody)
    rnd_coefs = random_coef(receiver_node_id, len(rref_custody_data), seq_no)
    data_vector = linear_combination(rref_custody_data, rnd_coefs)
    custody_proofs = [e.proof for e in da_store.custody]
    return DaMessage(data_vector, Vector(custody_proofs), seq_no)

计算数据向量系数的秩。 秩等于 N 表示可以从数据向量恢复原始数据。

def rank(proof_matrix: Sequence[ProofVector]) -> int

发布

发布者应拆分数据并获得 OriginalData。

在传播数据本身之前，发布者应计算 Pedersen 承诺（大小为 32 * N），构建并传播带有这些承诺的区块。

然后，它应该使用数据向量（原始）及其证明来填充保管，这些证明只是标准基的元素：[1, 0, 0, ..., 0], [0, 1, 0, ..., 0]：

def init_da_store(data: OriginalData, da_store: BlockDaStore):
    for i,v in enumerate(data):
        e_proof = ProofVector(
            [CScalar(1) if index == i else CScalar(0) for index in range(size)]
        )
        da_store.custody += DataAndProof(v, eproof)

发布过程基本上与传播过程相同，不同之处在于，发布者在单轮中向单个对等方发送 S 条消息，而不是在传播期间仅发送 1 条消息。

def publish(da_store: BlockDaStore, mesh: Sequence[Peer]):
    # Letf the Peer undefined
    for peer in mesh:
        for seq_no in range(S):
            peer.send(
                create_da_message(da_store, peer.node_id, seq_no)
            )

接收

假设相应的区块已收到，并且在接收 message: DaMessage 之前已填充 BlockDaStore.commitment

从原始向量派生 ProofVector：

def derive_proof_vector(myNodeId: uint256, message: DaMessage) -> ProofVector:
    lin_c = randomCoef(
        myNodeId,
        len(message.orig_coefficients),
        message.seq_no)
    return linear_combination(message.orig_coefficients, lin_c)

验证

首先对消息进行验证：

def validate_message(message: DaMessage, da_store: BlockDaStore):
    # Verify the original coefficients are in Reduced Row Echelon Form
    assert is_rref(message.orig_coefficients)
    # Verify that the source vectors are linear independent
    assert rank(message.orig_coefficients) == len(message.orig_coefficients)
    # Validate Pedersen commitment
    proof = derive_proof_vector(my_node_id, message)
    validate_pedersen(message.data_vector, da_store.commitment, proof)

存储

收到的 DataVector 已添加到保管。

sample_matrix 正在累积所有原始系数，并且只要矩阵秩达到 N，采样过程就成功

def process_message(message: DaMessage, da_store: BlockDaStore) -> boolean:
    da_store.custody += DataAndProof(
        message.data_vector,
        derive_proof_vector(my_node_id, message)
    )
    da_store.sample_matrix += message.orig_coefficients
    is_sampled = N == rank(da_store.sample_matrix)
    return is_sampled

is_sampled == true 表示我们 [几乎] 100% 确定向我们发送消息的对等方集体拥有 100% 的信息来恢复数据。

传播

当 process_message() 返回 True 时，这表示采样成功并且保管已填充足够的向量。 从现在开始，该节点可以开始创建和传播其自己的向量。

我们将向量发送给网格中尚未向我们发送任何向量的每个对等方：

## mesh: here the set of peers which haven't sent any vectors yet
def propagate(da_store: BlockDaStore, mesh: Sequence[Peer]):
    for peer in mesh:
            peer.send(
                create_da_message(da_store, peer.node_id, 0)
            )

优点和缺点

优点

• 要传播、保管和采样的总数据大小是原始数据大小的 x1（加上大约 20% 的系数开销，对于 S = 32）（与 PeerDAS 的 x2 和 FullDAS 的 x4 相比）
• 我们可以具有高达 32 的“分片因子”（或者对于更多修改来说，可能更大），这意味着每个节点只需要下载和保管原始数据大小的 1/32。（与当前 PeerDAS 方法中的 1/8 相比：来自 64 个原始数据的 8 列）
• 通过仅具有 S 个 任何 常规诚实节点即可获得可用数据并对其进行恢复
• 该方法“你采样什么就保管和提供什么”（类似于 PeerDAS 子网采样，但与完全分片对等采样不同）。 此处描述了有关对等方采样方法的担忧 here
• 由于不涉及列切片，因此单独的 blob 可能仅跨越多个原始数据向量，因此采样过程可能会有效地从 EL blob 事务池（又名 engine_getBlobs()）中受益
• 没有可能容易受到女巫攻击的较小子网
• 由于节点需要来自 任何 对等方的 S 条消息，因此传输级别上的数据重复可能会更低
• RLNC + Pedersen 可能比 RS + KZG 消耗更少的资源

缺点

• 承诺大小增长为

O(S2)，而由于系数导致的消息大小开销增长为

O(S3)。

• 仍然需要估计传播延迟，因为节点可能仅在完成其自己的采样后才传播数据
• 对于乐观情况，采样的最小对等方数为 32（与 PeerDAS 中的 8 个相比）

待证明的陈述

上述算法依赖于许多 [尚未模糊] 的陈述，目前需要对其进行证明：

1. 由超级节点返回的带有请求的随机系数的有效线性组合证明了响应节点可以访问完整数据（足够的向量来进行恢复）。 这个陈述看起来并不难证明
2. 如果全节点声称它具有构成系数子空间的基向量，则如果节点从该子空间请求随机向量并获得有效的数据向量，那么它将证明响应节点确实具有声明的子空间的基向量。 该证明可能是陈述 (1) 的概括
3. Fp 上的 EC 与子域 C2 有意义且安全
4. 用于零 RRT 采样的 RREF 基形式的技巧实际上有效
5. 所描述的算法在完整的 N 维空间中，在 hones 节点之间产生均匀分布的基向量。 存在一个非常小的 E（大约 1-3），使得任何随机选择的 S + E 节点的基向量的秩将以某个“非常高”的概率为 N。 在拜占庭环境中，情况也应该如此

• 原文链接： hackmd.io/jR2fEXUnRzKPHw...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～