SubnetDAS - 一种中间数据可用性抽样方法 - 分片
- 以太坊中文
- 发布于 2023-11-11 13:50
- 阅读 923
本文提出了一种名为 SubnetDAS 的中间数据可用性抽样(DAS)方案,旨在弥合 EIP-4844 和完整 Danksharding 之间的差距。该方案为每个样本设立一个子网,节点通过连接到相应子网来获取样本,从而在不影响网络活跃度和增加节点要求的前提下,实现更高的扩展性。同时,该方案牺牲了查询的不可链接性,但并不影响整个链的可用性保证和Rollup的安全性。
SubnetDAS – 一种中间的 DAS 方法
作者: Francesco 和 Ansgar。感谢 Mark Simkin 在安全分析方面的讨论和帮助,以及 EF 研究团队的各位成员提供的反馈。
这是一种基于子网的 DAS 提案,旨在弥合 EIP-4844 和完整 Danksharding 之间的差距,就像 peerDAS 一样。我们提出了一种 DAS 构造,其中每个样本都有一个子网,节点通过连接到这些子网来获取它们的样本。我们认为,与 EIP-4844 相比,它可以在不危及整个网络的活跃性或增加节点要求的情况下,提供更大的规模。
为此,我们确实牺牲了一些东西,即查询的不可链接性,或者更确切地说,是在此 DAS 框架内稍后解决此问题的可能性。要检索样本,节点必须加入相应的子网,并且在尝试这样做时,它会暴露其查询。这使得攻击者只能发布这些样本,从而说服它相信数据是可用的,而实际上并非如此。查询的链接性是所有 DAS 构造都面临的问题,但特别难以看出如何在基于子网的构造中解决它。它不会影响整个链的可用性保证,因此也不会影响 Rollup 的安全性,但它确实削弱了完整节点针对双重支出的安全性。我们将在稍后详细讨论这个问题,并认为这种削弱并不像看起来那么严重,并且对于中间 DAS 解决方案来说,这可能是一个明智的权衡。
为什么选择 SubnetDAS
我们认为子网是中间解决方案的主要网络结构的合理候选者,原因如下:
- 较少的网络未知因素:子网是经过尝试和测试的以太坊网络基础设施的一部分,因为自 Beacon Chain 启动以来,认证子网就一直在使用。新颖之处在于使用了更多的子网,但这将通过完整节点加入多个子网来抵消,因此每个子网仍应包含足够多的节点。
- 规模:在带宽要求与 EIP-4844 相似的情况下,我们认为 subnetDAS 可以实现与完整 Danksharding 相似的规模。使用我们稍后给出的示例参数,吞吐量将为每个Slot 16 MiB,同时要求完整节点参与子网,其每个Slot的总数据分配为 256 KiB,验证者为每个Slot 512 KiB,大致与 4844 一致。
-
未来兼容性:我们认为子网基础设施即使在 DAS 的未来迭代中也会被使用,因此这种努力是可重用的:
-
无论 DAS 的最终网络构造是什么,完整 Danksharding 的网络结构可能都将涉及子网,其中 Danksharding 正方形的行和列被分发,并且至少验证者会加入这些子网以下载分配给他们保管的行和列(peerDAS 中也假设了这一点)
-
即使在以后的迭代中,对于验证者的分叉选择,使用某种形式的 subnetDAS 可能仍然有意义,这不需要使用完整节点在其分叉选择中使用的相同 DAS 构造来跟踪链并确认交易(有关详细信息,请参见此处)。当用于此目的时,subnetDAS 的弱点是可以接受的或无关紧要的:
-
查询的链接性无关紧要,因为对于验证者的分叉选择,我们只关心全局可用性保证,而不是单个可用性保证(不必担心双重支出保护,因为这不用于确认交易)。
-
可以预期验证者比完整节点具有更高的带宽要求,因此即使对于长期而言,为验证者保持与 4844 相似的带宽要求可能也是可以的。
-
即使在以后的迭代中,也可以选择使用 subnetDAS 作为分叉选择过滤器,同时仅作为确认规则的一部分使用一些额外的采样(同样,有关详细信息,请参见 此处)。例如,完整节点可以仅使用 subnetDAS 进行分叉选择来跟踪链(验证者参与共识),同时仅进行一些对等采样来确认交易。对等采样的活跃性失败只会影响完整节点确认交易的能力,而不会影响 p2p 网络、共识和超级完整节点的交易确认。这种额外的采样甚至可以是可选的,让完整节点在确认安全性和活跃性之间选择自己的权衡。与前一点一样,由于作为确认规则的一部分进行的额外采样,查询的链接性将无关紧要。
-
构造
示例参数
| 参数 | 值 | 描述 |
|---|---|---|
| b | 128 | Blob 的数量 |
| m | 2048 | 列子网的数量 = 样本的数量 |
| k | 16 | 每个Slot的样本 = 每个节点的列子网 |
| r | 1 | 每个验证者的行子网 |
Blob 大小为 128 KiB,与 EIP-4844 相同,未扩展数据的总吞吐量为每个Slot 16 MiB。
数据布局
- 我们使用 1D 扩展,而不是 2D 扩展。Blob 在水平方向上扩展,并在垂直方向上堆叠。与 Danksharding 矩阵相同,但没有垂直扩展。
- 生成的矩形被细分为 m 列。使用示例参数,每列的宽度为 4 个字段元素(每个扩展 Blob 为 256 KiB,或 8192 个字段元素)。每列是一个样本。使用示例参数,样本的大小为 128*4*32 字节 = 16 KiB
子网
- 列子网:每列(样本)对应于一个列子网。列子网用于采样,所有完整节点都连接到其中的 k 个。
- 行子网:每行(一个扩展 Blob)对应于一个行子网,该子网用于重建。只有验证者需要连接到行子网,并且他们连接到其中的 r 个。
使用示例参数,每个列子网拥有 k/m = 1/128 的所有完整节点,并且每个行子网拥有 r/n = 1/128 的所有验证者
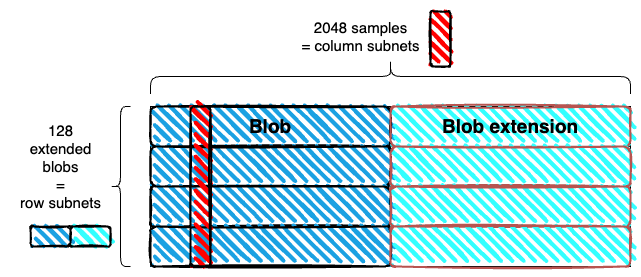
分发
Blob 在行子网中分发,样本在列子网中分发,同时进行。
采样
完整节点通过连接到相应的子网来查询每个Slot的 k 个样本。这只是对 1D 扩展进行采样,但样本是“长的”(列而不是点)。

使用示例参数,总共为 16^2 = 256 KiB,甚至低于 EIP-4844(对于验证者,还需要从行子网下载 r=1 扩展 Blob 的额外负载,额外增加 256 KiB)。
子网选择和数据可检索性
保留期内的数据可检索性提出了与此处类似的问题。为了解决这些问题,子网的轮换可以错开,并在数据保留期的时间范围内进行。在 subnetDAS 中这样做所产生的影响与在 peerDAS 中所产生的影响截然不同,因为子网的选择就是样本的选择,因此不每Slot轮换子网的选择意味着始终对相同的索引进行采样。
为了解决这个问题,我们可以让节点连接到 2k 个子网,其中 k 个是稳定的,k 个是每Slot轮换的。连接到前者纯粹是为了帮助提高子网密度和数据可检索性,而后者实际上用于采样。尽管如此,subnetDAS 无论如何都特别容易受到查询的链接性的影响,因此即使在这种情况下,稳定的子网选择也可能是有意义的。
重建
本地重建可以在行子网中进行。如果行子网中缺少某些数据,但列子网中存在,则同时位于两个子网中的验证者会在行子网中 Gossip 缺失的数据。一旦 > 50% 的扩展 Blob 可用,行子网中的所有验证者都会在本地重建它,然后将此行中的任何数据(他们缺少的数据)转发到他们的列子网。
安全性
我们分析了这种构造的两个安全方面(同样,有关安全概念的更多详细信息,请参见此处):
- 全局安全性:除了可以忽略不计的概率外,不可用数据会被除少数完整节点之外的所有节点拒绝(具体而言,我们可以设置一个可以容忍的最大完整节点比例,这些节点可能不会拒绝不可用数据)。
- 客户端安全性:客户端不会被说服相信不可用数据是可用的,除非概率可以忽略不计。
这些与完整节点的两个角色相对应:有助于强制执行网络规则,并允许与链进行最小信任的交互。第一个安全属性是使完整节点能够有助于强制执行构建在以太坊上的 Rollup 的规则的原因,最终保证了它们的安全性,前提是只有少数完整节点视为规范的链永远不会最终成为以太坊链,即使所有验证者都是恶意的。重要的是,这在即使对手提前知道所有查询的情况下也成立。
客户端安全性和查询不可链接性
第二个概念更加强大:我们要求根本无法欺骗任何采样节点(除非概率可以忽略不计)。为了实现这一点,我们不能假设对手提前知道所有查询。实际上,它需要查询不可链接性,即隐藏一组查询来自同一节点/参与者的能力,因为如果没有这种能力,对手始终只能提供单个节点要求的数据。
如果 Rollup 在较弱的概念(全局安全性)下是安全的,并且数据可用性的全部意义在于让 Rollup 使用它,那么我们为什么需要这种更强的安全概念?这是因为 DA 层与以太坊链的其余部分紧密耦合:如果某些 Blob 数据不可用,完整节点只会忽略该链。诱骗完整节点认为不可用数据是可用的,可能会使它们遭受安全违规,即双重支出:他们确认有效链中的交易看起来安全且可用,但实际上不可用,因此最终不会成为规范的以太坊链。这适用于确认以太坊交易以及 Rollup 交易,因为 Rollup 状态是从规范的以太坊链派生的。
以太坊交易
我认为引入没有查询不可链接性的 DAS不会对以太坊完整节点针对双重支出的安全性产生太大的改变。有两种情况,基于完整节点首先使用的确认规则:
- 同步确认规则:这些节点不等待最终性,而是使用一个规则(例如 这个规则),该规则做出同步假设和诚实多数假设。如果后者不满足(即在 51% 攻击中),那么该规则无论如何都是不安全的,并且可能会发生双重支出。如果后者满足,我们可以保证确认的链是可用的,因为只有一小部分诚实的验证者可能会被诱骗投票支持不可用的链。换句话说,由于 DAS 故障,诚实多数可能会略有削弱。因此,在没有 DAS 的情况下,同步确认规则在它所要求的相同假设下仍然是安全的。
- 最终性:如果一个节点今天等待最终性,它将获得保证,除非存在两个冲突的最终确定区块,否则它不会受到双重支出的影响,这需要 1/3 的验证者集提交可削减的违规行为。使用 DAS,也可能最终确定的区块根本不可用,而没有冲突的最终确定。请注意,这仍然需要接近恶意的超级多数,同样是因为只有一小部分诚实的验证者可能会被说服投票支持不可用链。另一方面,它似乎并没有给出针对双重支出的经济最终性保证。完整节点可能无法识别最终确定的链不可用,并在其中确认交易。如果它永远不可用,则社会共识最终将不得不进行干预并协调从完全可用的链开始的分叉,从而导致完整节点的安全违规。原则上,这不需要涉及任何削减,从而否定了任何经济最终性。实际上,社会共识可以选择削减任何投票最终确定不可用链并且未能在特定截止日期前生成他们应该保管的数据的验证者。如果该链确实最终变得不可用,这将意味着几乎超级多数的验证者未能生成他们保管的数据,并且可能会被削减。
此外,请记住,那些交易大量价值并希望获得与今天的完整节点相同的针对双重支出的安全保证的人可以选择运行下载所有数据的超级完整节点,而且这肯定不是一个过高的成本。至少值得讨论的是,完整节点交易确认安全性的这种(我们认为较小的)安全降低是否真的值得坚持。
Rollup 交易
确认 Rollup 交易的安全性情况非常相似,但还有一些围绕有效性的考虑因素,同样取决于 Rollup 节点使用的确认规则。让我们假设基线确认规则是以太坊最终性,然后使用一些 Rollup 特定的条件对其进行增强。
对于有效性 Rollup,明智的选择显然是在确认之前等待有效性证明,尽管不一定是在以太坊本身上发布和验证它。这样的节点确实获得了与以太坊完整节点在确认最终确定交易时获得的完全相同的安全保证(模有效性系统中或验证器实施中的问题),因为有效性是有保证的。换句话说,唯一的攻击向量是与我们在上一节中讨论的相同类型的双重支出。
对于乐观 Rollup,有多种选择。可以运行 Rollup 完整节点并简单地验证所有状态转换,在这种情况下,显然没有额外的担忧。当然,这并不理想,因为原则上 Rollup 节点可能比以太坊节点重得多。它也可以只等待 Rollup 桥确认交易,这同样安全,但由于欺诈证明期,需要更长的确认期。另一种选择是侦听 p2p 网络上(启动消息)欺诈证明,这可以使用比桥更短的欺诈证明期来完成。如果不可用数据已最终确定并且节点被诱骗认为它是可用的,则可以诱导运行这种快速确认规则的节点确认无效交易。
全局安全性
总结:即使对手提前知道所有查询,也无法说服超过一小部分采样节点相信不可用数据是可用的
对于自适应对手,它在决定使哪些数据可用之前一次性考虑所有查询,当从总共 m 个样本中下载 k 个样本时,成功定位 \epsilon 分数的 n 个节点的概率可以用 \binom{n}{n\epsilon}\binom{m}{m/2} 2^{-kn\epsilon} 来联合 bound:对手选择 n\epsilon 节点的子集,从 \binom{n}{n\epsilon} 个可能的子集中选择一个子集,一个由至少 \frac{m}{2} 个样本组成的子集,使其不可用,从 \binom{m}{m/2} 个这样的子集中选择一个子集,并且在给定这些选择的情况下,成功的概率为 2^{-kn\epsilon}。逼近二项式系数,我们得到 \left(\frac{2^{n}}{\sqrt{\frac{n\pi}{2}}}e^{-\frac{\left(n\ -\ 2n\epsilon\right)^{2}}{2n}}\right)\frac{2^{m}}{\sqrt{\frac{m\pi}{2}}}2^{-kn\epsilon} = \left(\frac{2^{n}}{\sqrt{\frac{n\pi}{2}}}e^{-\frac{\left(n\ -\ 2n\epsilon\right)^{2}}{2n}}\right)\frac{2^{\left(m-kn\epsilon\right)}}{\sqrt{\frac{m\pi}{2}}}, 并且我们希望这个值 < 2^{-30} 或类似的值。这给了我们 (n + m - kn\epsilon) - \log_{2}\left(e\right)\frac{n\left(1\ -\ 2\epsilon\right)^{2}}{2} < \log_2(\sqrt{nm}\frac{\pi}{2})-30
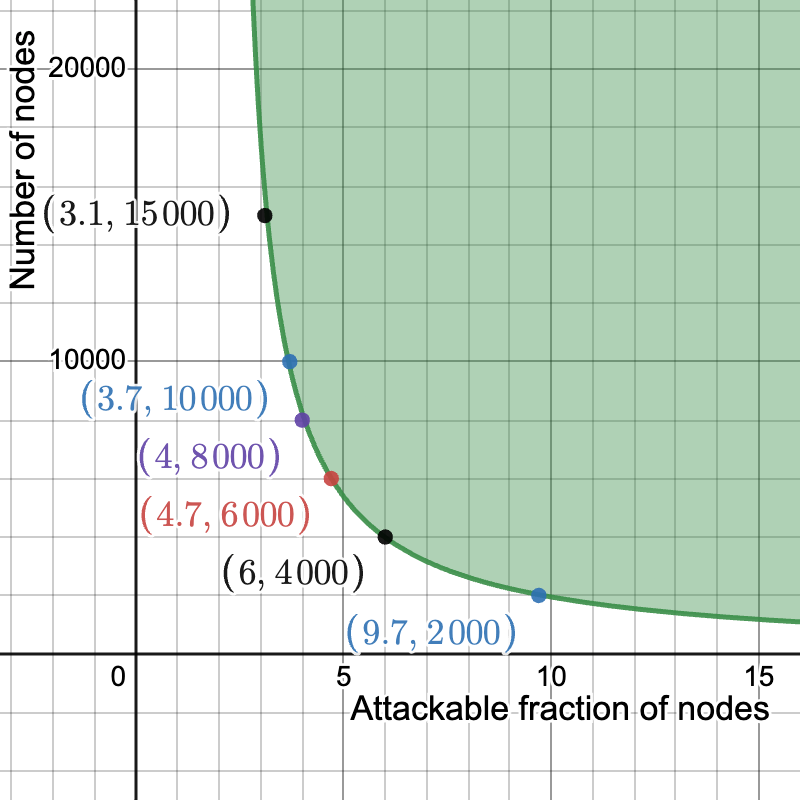
在下面的图中,我们设置 k = 16 和 m = 2048。在 y 轴上,我们有 n,即节点的数量,在 x 轴上,我们有 \epsilon,即可被欺骗的最大节点比例(特别是在这里,概率 \ge 2^{-30},但结果对选择的失败概率几乎不敏感)。只要我们至少有 2000 个节点,不到 10% 的节点可以被欺骗性地说服存在不可用的数据。此外,在 6000 到 10000 个节点之间,可攻击节点的比例下降了 5% 到 4%。
(你可以在此处使用这些参数)
也许值得注意的是,在考虑提前知道所有查询的对手的这种分析中,具有 m = 512^2(在正方形上采样)和 k = 75 的完整 Danksharding 采样并没有做得更好。实际上,它表现得更糟,这仅仅是因为 m 有多大。这不应该完全令人惊讶,因为此构造中的节点需要下载更大比例的数据(0.256 KiB/32 MiB,或 1/128,与 37.5 KiB/128 MiB,或 ~1/3000 相比)。也就是说,这只是一个可能不严格的界限,因此一个坏的界限并不一定意味着安全性差。另一方面,如果该界限被证明是严格的,则意味着具有如此高的 m 的全局安全性不能抵抗完全自适应的对手,而是也需要对查询的不可链接性做出一些假设。
安全性-吞吐量-带宽权衡
当然,我们可以通过恶化其他两个中的一个或两个来提高带宽要求、安全性和吞吐量中的任何一个。例如,将 Blob 的数量减半为 b = 64,并将样本的数量加倍为 k=32 将保持带宽要求不变,同时使吞吐量减半,但会给我们一个更好的安全曲线。另一方面,我们可以通过设置 b = 256 和 k = 8 来使吞吐量加倍,同时保持带宽要求不变,从而牺牲安全性。在这里,我们比较 k=8,16,32 的安全性,即分别对应于最大吞吐量 32MiB、16MiB 和 8MiB。
(你可以在此处使用这些参数)
- 原文链接: ethresear.ch/t/subnetdas...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Vitalik的L2重置:以太坊为何需要此航向修正 257 浏览
- Vitalik: 重新评估以太坊 Layer2 363 浏览
- 通过实时证明实现 Rollup 间的同步组合 - Layer 2 232 浏览
- Ethrex L2:构建 Rollup 的一种不同方法 368 浏览
- 外部跨链桥 vs Rollup 的安全委员会 696 浏览
- Vitalik: 结合预确认与Based Rollup的架构,实现同步可组合性 472 浏览
- 区块链101:区块链的演进 762 浏览
- Celestia 2.0 愿景:所有市场上链 670 浏览
- 区块链 101:数据处理 1120 浏览
- 为什么许多团队的Layer 2迁移会失败(以及如何正确地进行迁移) 495 浏览
- Calldata 优化 1550 浏览
- 区块链扩容 1783 浏览

 \
graph800×800 52.1 KB
\
graph800×800 52.1 KB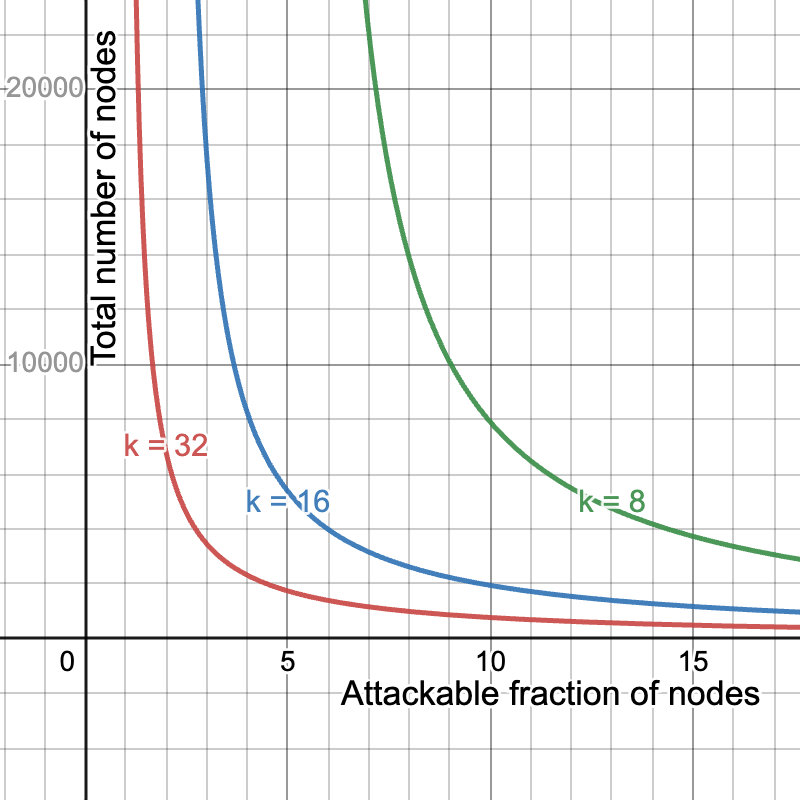 \
graph1800×800 42.1 KB
\
graph1800×800 42.1 KB
