论文评审 - 决策树预测和准确性的零知识证明

草稿模式

摘要

机器学习变得越来越重要，并已被广泛应用于实践中的各种应用。尽管取得了巨大的成功，但机器学习预测的完整性和准确性却引发了日益关注。声称能够实现高准确度的机器学习模型的可重复性仍然具有挑战性，而真实产品中机器学习预测的正确性和一致性缺乏任何安全保证。本文作者发起了零知识机器学习（ZKML）的研究，并提出了零知识决策树预测和准确性测试的协议。

• 本文提出了一种新颖的方式，证明决策树可以对给定数据点做出正确预测，而不泄露有关决策树本身的任何信息。这被称为零知识决策树预测协议。
• 该协议分为两个阶段：设置阶段和证明阶段。在设置阶段，决策树以线性时间进行编码，时间复杂度与树的大小相关。在证明阶段，预测的计算方式仅依赖于预测路径的长度和数据点的特征数量。
• 该协议借用了许多来自零知识证明领域的高级技术，应用于RAM模型中的计算，但在非黑盒方式上进行了适应，以适合决策树的设置。
• 该协议将决策树预测转换为一个小电路，大小为 $O(d + h)$，其中 $d$ 是特征的数量，$h$ 是树的高度。
• 本文还扩展了协议，以证明决策树在测试数据集上的准确性，这被称为零知识决策树准确性协议。
• 准确性协议有两个优化，减少了零知识证明后端的哈希数量，使其正好等于决策树中的节点数量。这个数字不依赖于测试数据集的大小，如果树是非平衡的，可能比 $2^h$ 小得多。
• 本文在多个真实世界的数据集上实现并评估了这两个协议。结果显示，对于一个具有 23 层和 1,029 个节点的大型决策树，仅需 250 秒即可生成其在包含 5,000 个数据点和 54 个特征的测试数据集上的准确性的证明。证明的大小为 287KB，验证所需时间为 15.6 秒。

论文引用

Jiaheng Zhang, Zhiyong Fang, Yupeng Zhang, and Dawn Song. 2020. Zero Knowledge Proofs for Decision Tree Predictions and Accuracy. 在2020年ACM SIGSAC计算机与通信安全会议论文集中（CCS '20）. 计算机协会，纽约，NY，美国，2039–2053. https://doi.org/10.1145/3372297.3417278

零知识证明

本文提出使用零知识证明（ZKP）来确保机器学习预测和准确性的完整性，而不泄露任何有关模型本身的信息。零知识证明允许证明者生成一个简短的证明，以令任何验证者相信，在证明者的公共输入和秘密输入上运行公共函数的结果是正确的。秘密输入通常被称为见证或辅助输入。零知识证明保证，如果证明者在计算结果时作弊，验证者将以压倒性的概率拒绝，同时证明不透露任何关于秘密的信息，除了结果。

• 一个关于 $NP$ 关系 $R$ 的零知识知识论证使用算法元组 $(G, P, V)$，并具有以下特性。
• 该论证系统的第一个特性是 完整性，这意味着对于由 $G(1^λ)$ 生成的每个公共参数 $pp$，如果 $(x; w) ∈ R$ 且 $π ← P(x, w, pp)$，那么验证者 $V$ 根据 $(x, π, pp)$ 接受该证明的概率为 $1$。
• 第二个特性是 知识健壮性，这确保任何计算上有限的证明者 $P^∗$ 不能在没有见证 $w$ 的情况下让 $V$ 相信假命题 $(x; w) ∉ R$。这一特性由存在一个 $PPT$（概率多项式时间）提取器 $E$ 保证，该提取器可以从执行过程和 $P^∗$ 的随机性中提取 $w$，概率极小。
• 第三个特性是 零知识，这意味着存在一个 $PPT$ 模拟器 $S$，可以在不了解见证 $w$ 或任何关于 $(x; w)$ 的信息的情况模拟任何验证者 $V^∗$ 的视图。该特性确保证明不会透露任何关于见证或声明的信息，超出已知的信息。
• 最后，定义引入了 简洁 论证系统的概念，限制 $P$ 和 $V$ 之间的总通信（证明大小）为安全参数 $λ$、输入大小 $x$ 和见证大小 $|w|$ 的对数的多项式关系。这一特性确保证明可以高效验证和传输，而不泄露任何额外信息。

零知识决策树

模型引入了一个配备有预训练决策树的知识型证明者。证明者通过事先承诺决策树来主动进行。随后，验证者对数据样本的预测提出查询。为了验证其准确性，证明者生成一个可信的证明和结果。

但是首先，让我们介绍一下概念和定义：$F$，一个有限域；$T$，一个具有高度 $h$ 和 $N$ 个节点的二叉决策树 $(N ≤ 2^h −1)$；以及 $D$，包含具有 $d$ 个特征的数据点的测试数据集，其中每个数据点 $a ∈ F^d$。此外，$[M]$ 表示所有目标分类的集合。决策树算法，记作 $T : F^d → [M]$，负责将数据点映射到其对应的分类。当一个数据点 $a ∈ D$ 被输入到决策树时，$T(a) ∈ [M]$ 是分类预测。

贯穿始终，该方案假定两方都知道决策树的高度（或一个上界）。此外，他们将 $comT$ 作为决策树的承诺，$y_a$ 作为决策树为数据点 $a$ 返回的类别，并且 $π$ 作为证明者巧妙制作的证明。最后，${0, 1}$ 表示验证者的输出，指示是否接受或拒绝分类和证明。

零知识决策树方案（zkDT）由四个算法 $G$、$Commit$、$P$ 和 $V$ 构成：

1. $pp ← zkDT.G(1^λ)$ 算法：在给定的安全参数下，生成公共参数 $pp$。

2. $comT ← zkDT.Commit(T , pp, r)$ 算法：该步骤包含证明者使用随机点 $r$ 承诺决策树 $T$。

3. $(y_a, π ) ← zkDT.P(T , a, pp)$ 算法：在给定数据点 $a$ 时，执行决策树算法，生成 $y_a = T(a)$ 和相应的证明 $π$。

4. ${0, 1} ← zkDT.V(comT , h, a, y_a, π , pp)$ 算法：此时，验证者验证 $a$ 的预测、决策树返回的分类 $y_a$ 和证明者提供的证明 $π$。

zkDT构造的直观理解

以下是描述zkDT具体构造的序列图。

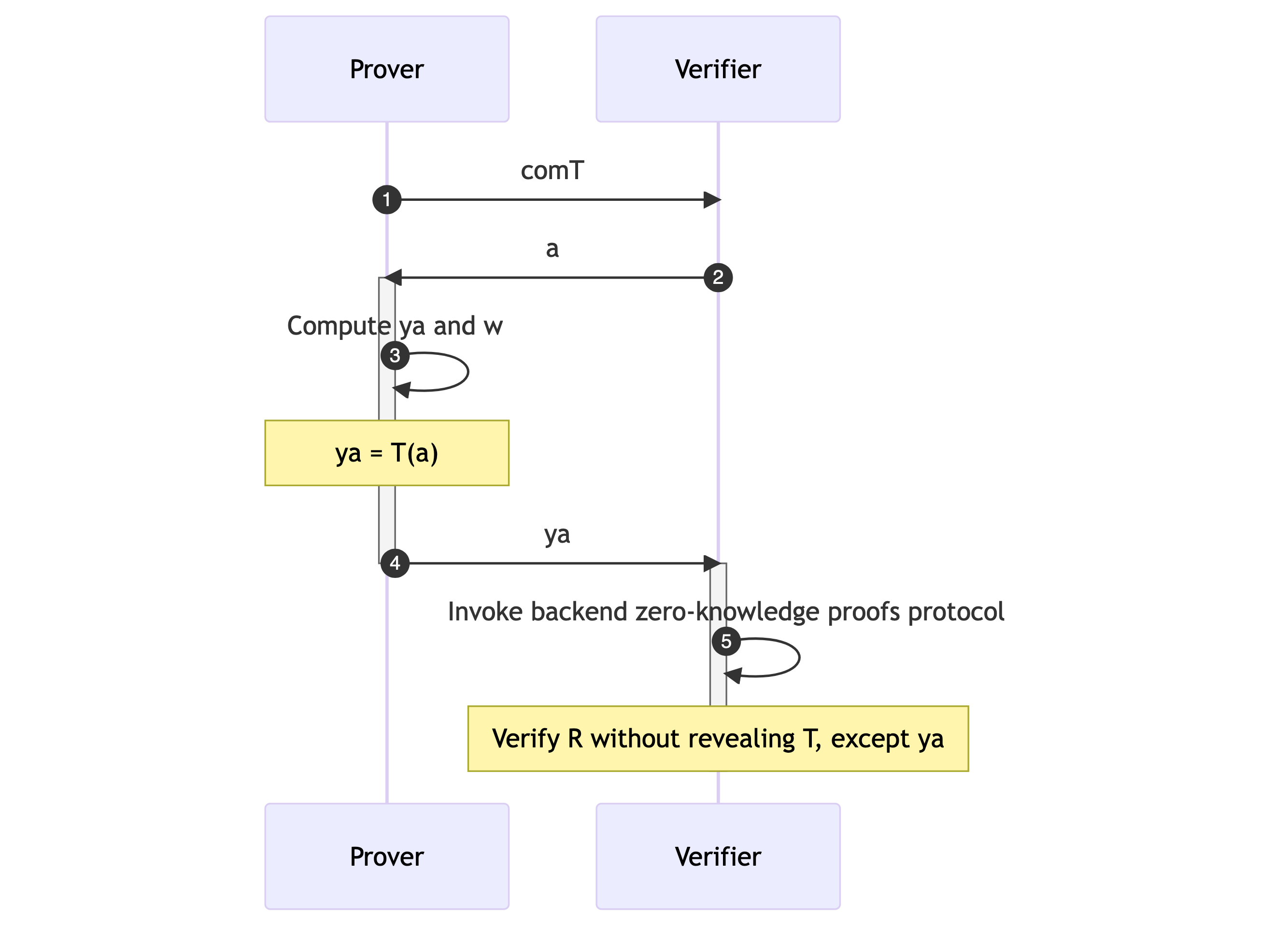
• zkDT构造的一般思路涉及证明者 $P$ 向验证者 $V$ 发送决策树 $T$ 的承诺 $comT$。
• 在收到来自验证者的数据样本 $a$ 后，证明者计算 $y_a$ 和相应的见证 $w$，以证明 $y_a = T(a)$，然后将 $y_a$ 发送给验证者。
• 这种关系 $R = ((y_a, a, comT); w)$ 被视为上述 ZKP 中描述的 $NP$ 关系。
• 然后验证者和证明者调用后端的零知识证明协议，以验证关系 $R$，而不泄露有关 $T$ 的任何信息，除了 $y_a$。
• 这种方法确保了决策树隐私的保留，同时仍然允许做出和验证准确预测。

认证决策树

本文引入了认证决策树（ADT）的概念，这是一种通过承诺方案进行认证的决策树。ADT在提出的零知识决策树预测和准确性测试协议中使用。ADT的构造通过对决策树根与随机点的连接进行哈希，以生成承诺。

• 采用一种简单的方法对决策树进行承诺是计算整个树的哈希值，但这在证明预测时会产生高开销。
• 另一种方法是对决策树中的所有节点使用默克尔哈希树，但这在零知识证明的后端中仍然引入了开销。

ADT的构造

本文描述了ADT的构造，这是通过对决策树根与随机点进行哈希以生成承诺。本文指出，为了在之后证明零知识性质，承诺必须采用随机化。

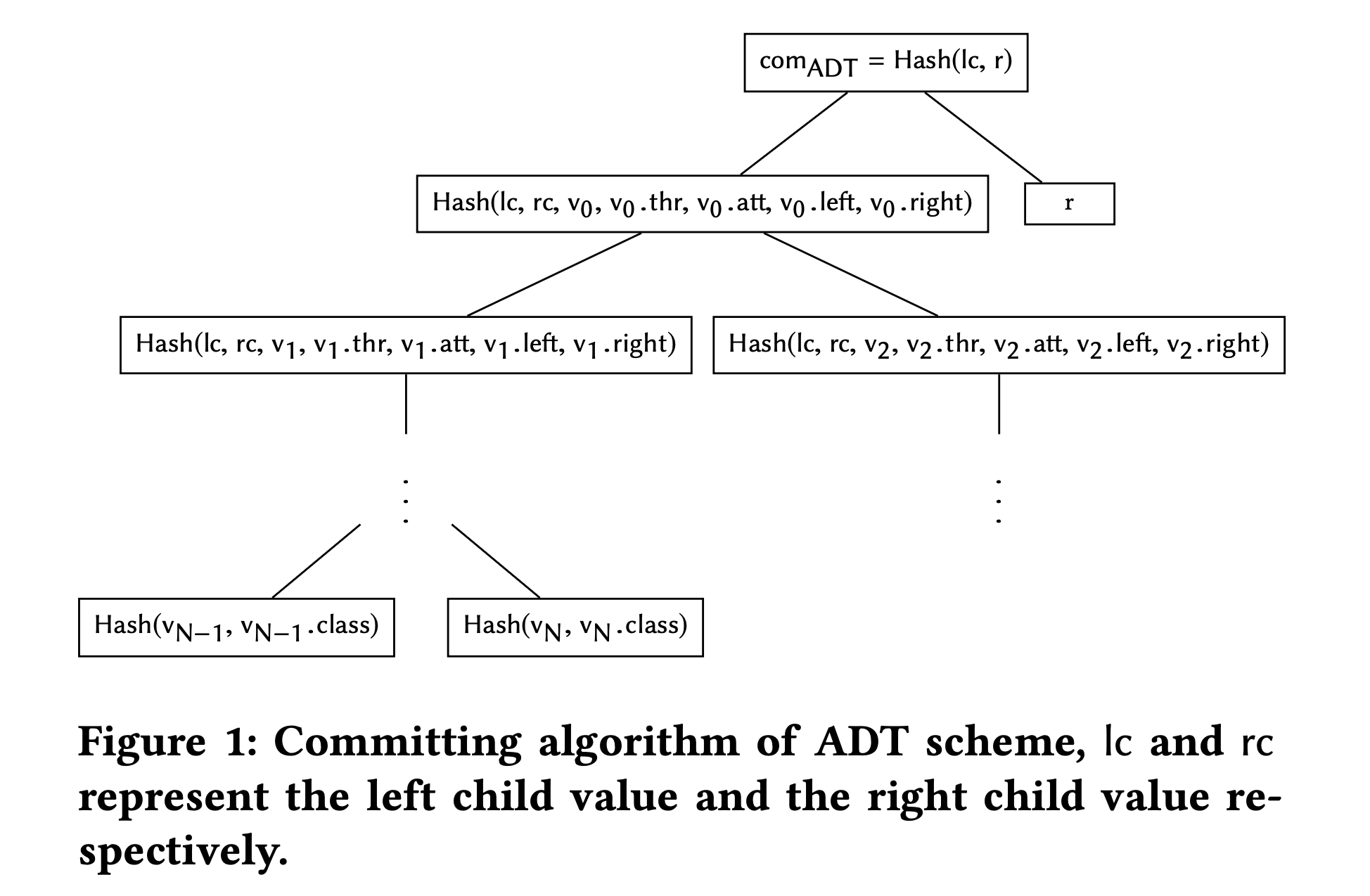
• ADT中的每个节点包含三部分信息：属性 $(v.att)$、阈值 $(v.thr)$，以及指向左子树和右子树的指针 $(lc, rc)$。
• 上图展示了ADT的构造，说明了如何利用其子节点的哈希和自身的属性及阈值计算中间节点的哈希。
• 属性和阈值值的加入确保了决策树的完整性，任何对树结构或值的篡改都将在验证过程中被发现。
• ADT的验证算法类似于默克尔哈希树，其中证明包括从根到叶节点的预测路径，该路径输出预测结果，以及沿预测路径节点的兄弟节点的哈希。
• 通过证明，验证者可以重新计算根哈希并与承诺进行比较，以确保预测的有效性。
• 使用ADT相比默克尔哈希树的优势在于，ADT的验证只需 $O(h)$ 次哈希，其中 $h$ 是决策树的高度，而默克尔哈希树需要 $O(h \log N)$ 次哈希，其中 $N$ 是树中的节点数量。
• zkDT的构造利用ADT有效地将决策树预测和准确性转化为零知识证明的陈述，从而允许决策树模型的拥有者在不泄露任何有关模型本身的信息的情况下，向他人证明其准确性。

在ADT的构造下，我们可以更新在ADT中使用的零知识证明算法的方法论。

• 为了证明方案的零知识特性，承诺必须是随机化的。这意味着随机点 $r$ 被添加到决策树的根，根与 $r$ 连接的哈希被用作最后的承诺。如上图所示。
• 本文所述的ADT并不需要支持动态插入和删除，以应用的目的，这显著简化了构造。
• 第一个算法 $pp ← ADT.G(1^λ)$ 从哈希函数家族中抽样一个抗碰撞哈希函数。
• 第二个算法 $comADT ← ADT.Commit(T, pp, r)$，从叶节点计算到 $T$ 根的哈希值，随机点为 $r$，如上图所示。
• 第三个算法 $πADT ← ADT.P(T, Path, pp)$，给定 $T$ 中的路径，包含沿路径所有节点的兄弟节点和上图中的随机性 $r$。
• 第四个算法 ${0, 1} ← ADT.V(comADT, Path, πADT, pp)$，给定路径和 $πADT$，沿路径重新计算哈希，将 $πADT$ 按上图相同的过程并将根哈希与 $comADT$ 进行比较。如果它们相同，输出 $1$，否则输出 $0$。
• 这些算法用于有效地将决策树预测和准确性转化为零知识证明的陈述。

证明预测的有效性

证明决策树中预测正确性的协议涉及在验证过程之上使用零知识证明，以保持预测路径和兄弟哈希的机密性（零知识）。该协议确保验证者仅收到一个二进制输出 $(1 \text{ 或 } 0)$，指示所有检查是否通过，从而实现了既可靠又具零知识性质。

以下步骤解释了论文中提出的用于验证决策树预测的高效零知识证明协议的设计。

• 该协议通过使用承诺决策树将预测的有效性转化为算术电路。
• 该电路的公共输入包括数据样本 $a$、决策树的承诺 $comT$ 和预测结果 $y_a$。
• 证明者的秘密见证包括预测路径 $a$ 和在ADT承诺中的随机性 $r$。
• 为了提高效率，证明者将预测路径上的节点的兄弟节点和按预测路径节点的 $v.att$ 排序的数据样本 $a$ 的排列 $\hat{a}$ 作为见证的一部分输入。
• 扩展见证的目的是检查数据样本和排序样本之间的排列，并验证承诺决策树中的预测路径。
• 整个电路由三个部分组成：验证决策树的预测算法，检查数据样本 $a$ 与排序样本 $\hat{a}$ 之间的排列，以及检查承诺决策树中的预测路径的有效性。
• 电路的输出为 $1$ 或 $0$，表示所有条件是否被满足或某些检查失败。

决策树预测

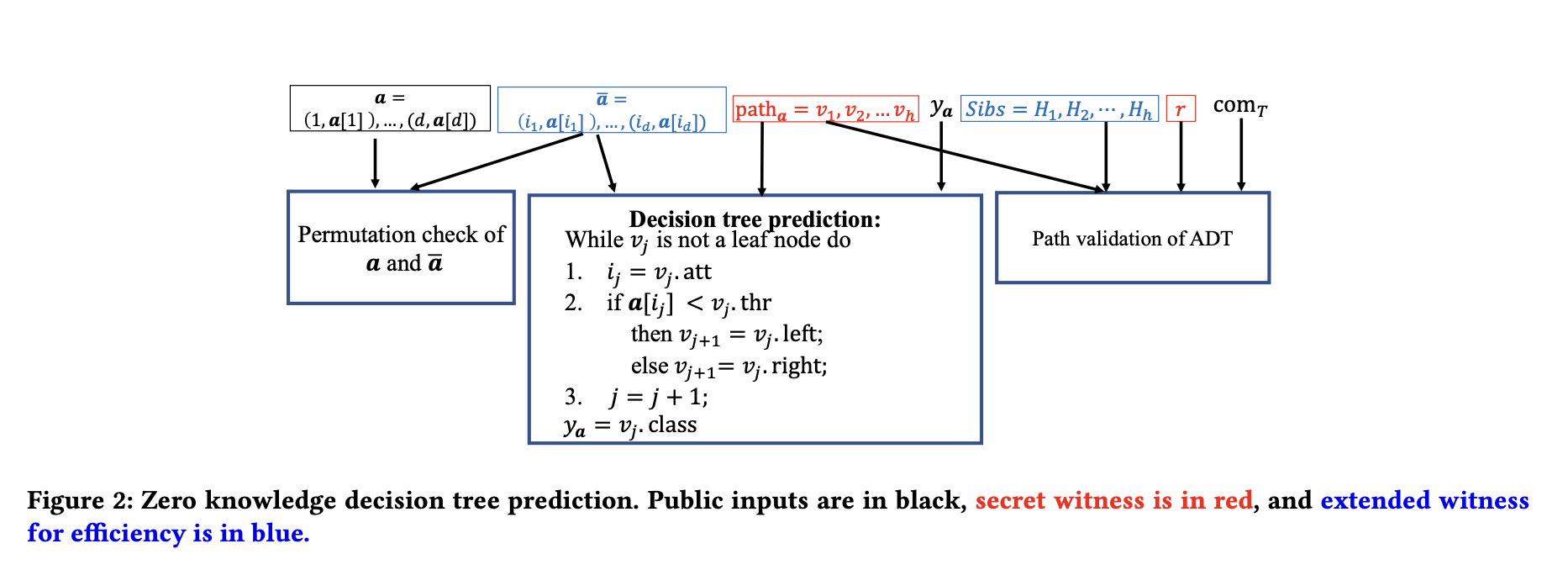
上图 2 描述了零知识决策树预测。

• 验证过程通过使用算术电路有效实施，辅以辅助输入 $\hat{a}$。
• 数据样本 $a$ 和 $\hat{a}$ 的表示略有修改，以成为索引-值对，其中 $a = (1, a[1]), . . . , (d, a[d])$ 和 $\hat{a} = (i_1, a[i_1]), . . . , (i_d , a[i_d])$。
• 电路检查预测路径上的每个内部节点 $v_j$（$j = 1, . . . , h−1$）是否满足 (1) $v_j.att = i_j$，以及 (2) 如果 $a[i_j ] < vj.thr$，则 $v{j+1} = vj.left$，否则 $v{j+1} = v_j.right$。
• 相等测试和比较使用电路基础零知识证明文献中的标准技术计算，借助辅助输入。
• 最后，电路检查是否 $y_a = v_h.class$。如果所有检查通过，电路输出 $1$，否则输出 $0$。
• 这一部分的总门数为 $O(d + h)$，渐进上与算法 1 的普通决策树预测相同。
• 如果 $h < d$，这在实践中通常成立，该电路只检查 $\bar{a}$ 中前 $h-1$ 对的索引。其余的索引可以是任意的，只要 $\bar{a}$ 是 $a$ 的排列。
• 证明者和验证者可以就预测路径的长度达成一致，并为每个数据样本构造一个单独的电路，或者使用树的高度作为上界为所有数据样本构造同一个电路。
• 这两种选择都被方案支持，并且渐近复杂度是相同的。然而，前者效率更高，但泄露了预测路径的长度。

排列测试

路径验证

零知识决策树预测协议

零知识决策树准确性

验证决策树准确性

本文提出了一种通过零知识证明验证决策树准确性的协议。该协议涉及证明者生成一个证明，以证明决策树

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～