Uniswap V3 详解
Uniswap v3 中的真实储备金
- RareSkills
- 发布于 2025-08-16 08:12
- 阅读 1696
本文深入探讨了 Uniswap v3 中真实储备金的概念,解释了如何根据流动性、价格以及上下限价格计算一个segment中的真实储备金,并提供相应的公式。文章还讨论了在当前价格超出segment范围时如何计算真实储备金,以及如何在实际交易中使用这些公式。
Uniswap v3 中的实际储备金
在上一章中,我们介绍了两个新概念:实际储备金和虚拟储备金。一个区间的实际储备金是指该区间内包含的代币数量——xr 个 X 代币、yr 个 Y 代币,或两者都有。
虚拟储备金是指如果该区间是无限曲线的一部分,该区间应有的代币数量。虚拟储备金是必要的,因为 Uniswap v3 中曲线区间的交换行为与 Uniswap v2 中的行为完全相同——也就是说,就好像这些区间实际上是 Uniswap v2 池中的无限曲线的一部分。
我们还推导了基于价格和流动性计算区间虚拟储备金的公式,但我们想要的是计算区间实际储备金的公式。这是本章的主要目标。
Uniswap v3 中的流动性、价格和虚拟储备金
在 Uniswap v3 中,流动性和价格定义如下:
$L^2 = xy$ $p = y/x$
其中 x 和 y 是虚拟储备金,p 是以 X 代币为单位的 X 代币价格。
正如我们在上一章中看到的,我们可以反转这些公式,并从 L 和 p 中推导出虚拟储备金 x 和 y,如下所示:
$x = L/\sqrt{p}$ $y = L\sqrt{p}$
仅凭这些信息不足以推导出区间的实际储备金,因为所有具有相同流动性且价格相同的区间将具有相同的虚拟储备金——无论它们的边界如何。
这可以在下面的动画中看到,该动画说明了两个具有相同流动性且价格相同的区间。它们的虚拟储备金相同,但它们的实际储备金不同。
<video src=" https://pub-32882f615aa84e4a94e1279ccf3ab85a.r2.dev/UniswapV3RealReserves/Realres11.mp4" type="video/mp4" autoplay loop muted controls>
因此,我们不能仅从价格和流动性推导出实际储备金——还必须考虑区间的边界。
一个区间的实际储备金
一个区间的实际储备金是指在该区间内可以进行交易的代币数量,直到价格达到该区间的边界。
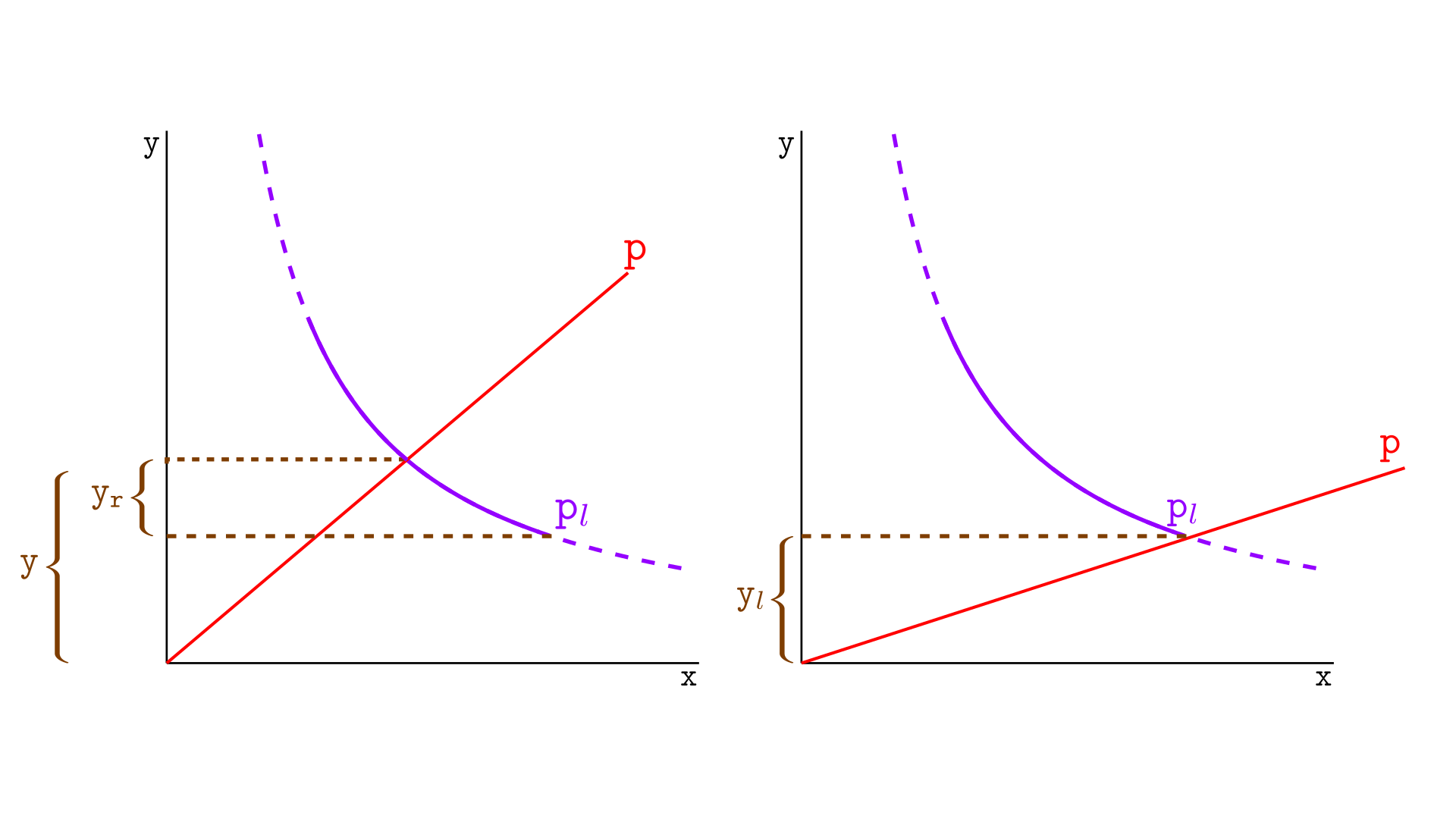
考虑下图所示的情况,其中价格在该区间内(左侧)。此时,池中具有 xr 个 X 代币的实际储备金和 yr 个 Y 代币的储备金。
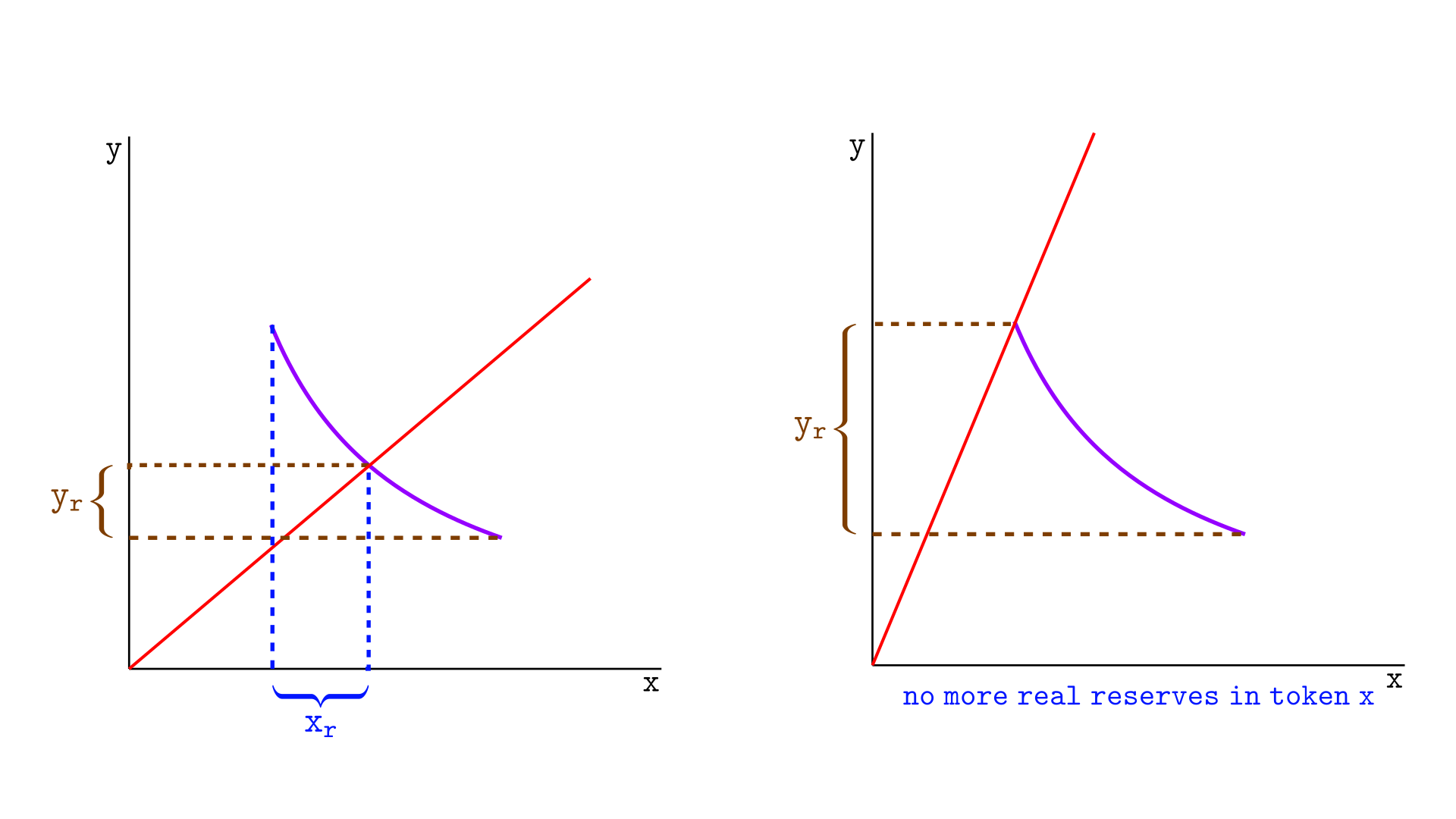
在上图的右侧,一次交换导致价格移动到上刻度,并且池现在仅持有 Y 代币的储备金——不再持有 X 代币。
这表明,一个区间中 X 代币的实际储备金 xr,是在将价格移动到上刻度的交换期间将离开该区间的代币数量。
同样的逻辑可以应用于 Y 代币的实际储备金,但现在是对于将价格移动到下刻度的交换,如下图所示。
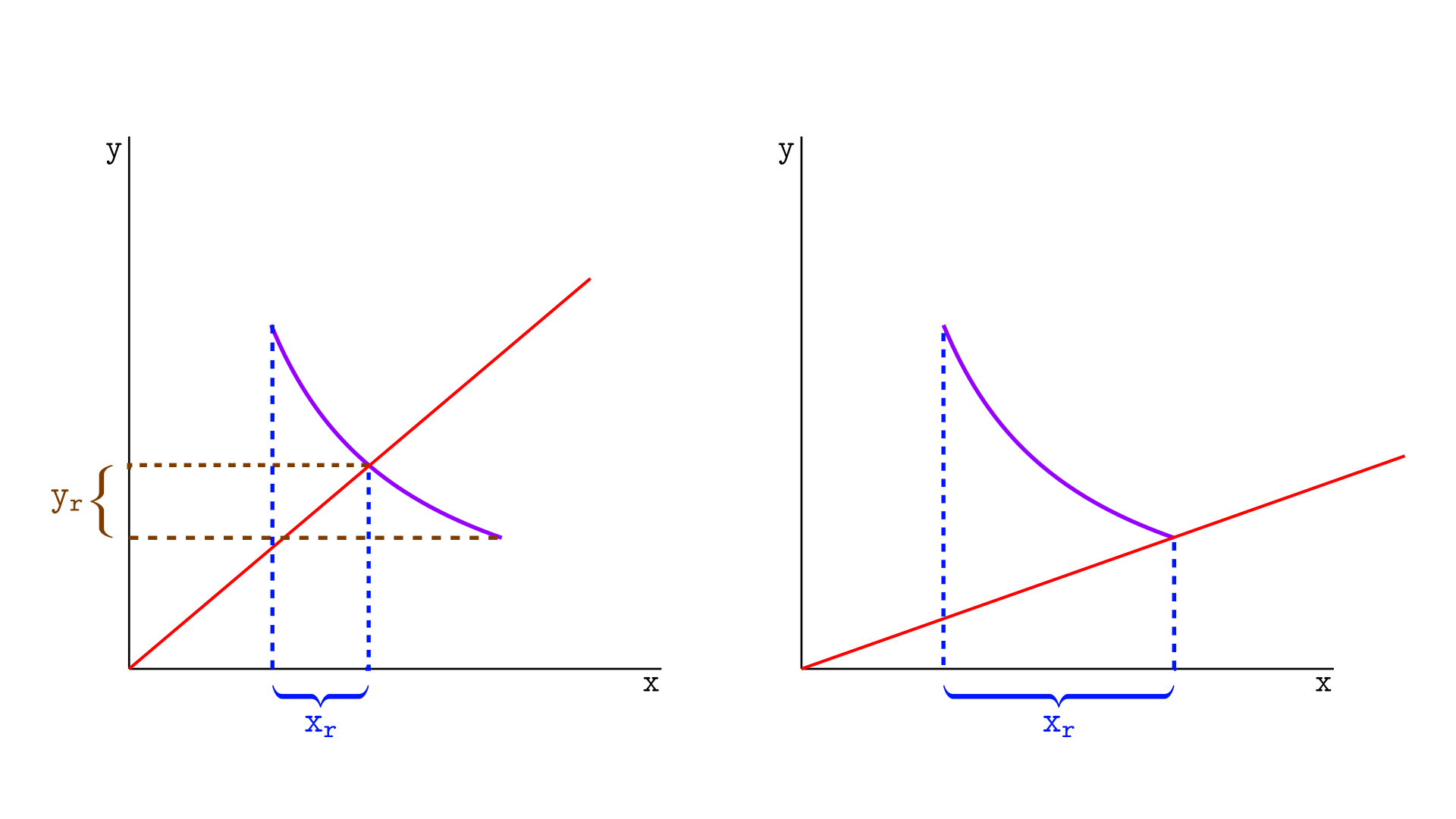
y 的实际储备金 yr,是在将价格移动到下刻度的交换期间将离开该区间的代币数量。
因此,如果我们能够计算出在第一个示例中有多少 X 代币离开了池,以及在第二个示例中有多少 Y 代币离开了池,我们将推导出实际储备金的公式。
我们_可以_做到这一点,因为我们知道如何在 Uniswap v2 中执行这些计算——并且在一个区间内,Uniswap v3 的行为与 Uniswap v2 完全相同。
推导 X 代币实际储备金的公式
在无限曲线的上下文中,我们可以轻松地计算出在移动价格的交换中离开池的 X 代币数量。让我们考虑一下价格从 p 开始移动到 pu,其中 pu 是上刻度的价格,如下图所示。
在左侧,X 的虚拟储备金由 x 给出(p 时的虚拟储备金)。在右侧,虚拟储备金由 xu 给出(pu 时的虚拟储备金)。在 Uniswap v2 中,这些是实际储备金,因此 x−xu 个代币将在此交换中离开池。
由于 Uniswap v3 具有与 v2 相同的行为,因此 x−xu 个代币也将在 Uniswap v3 中离开池——这些是此区间的 X 的实际储备金 xr。
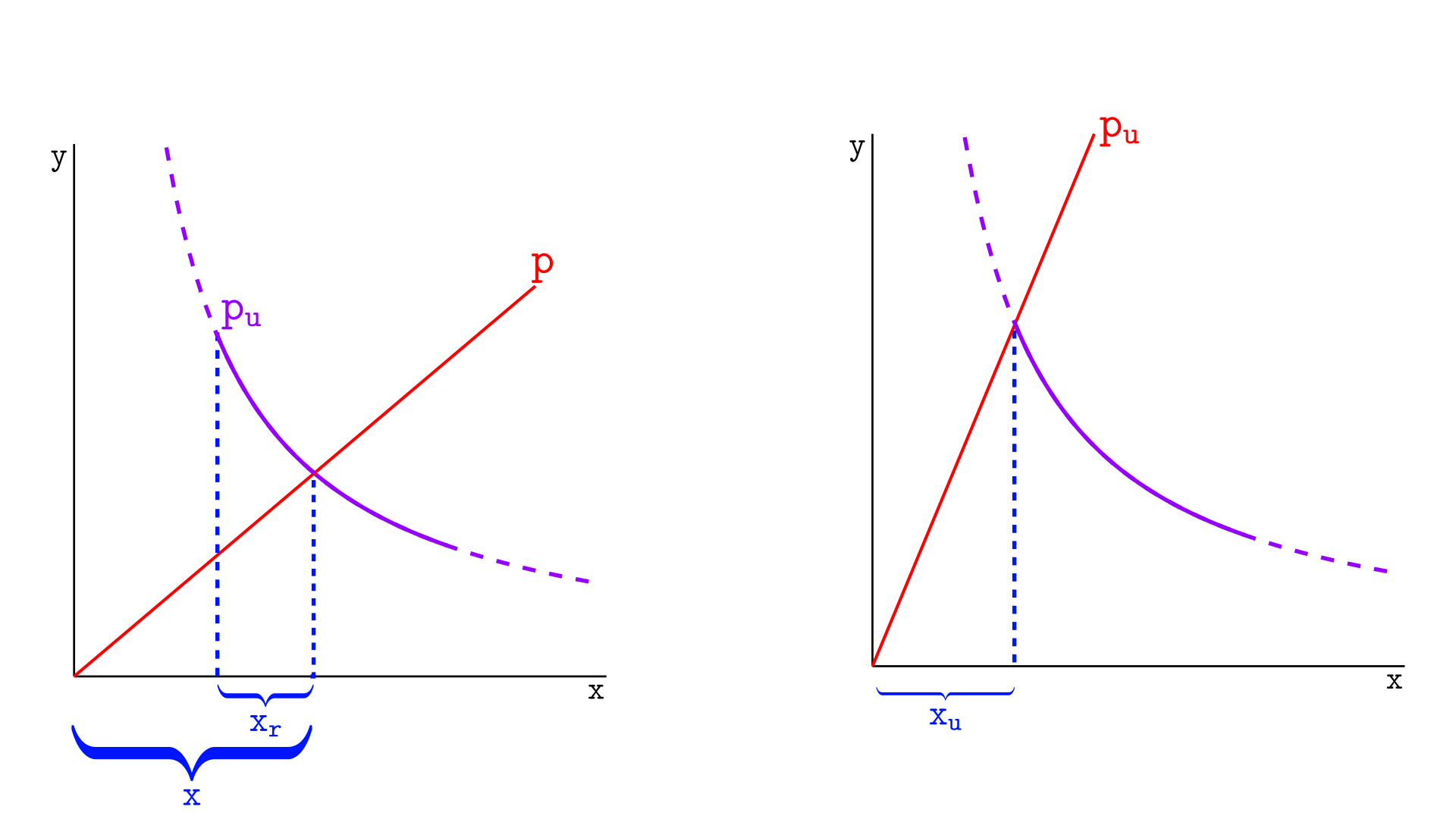
因此,
$x_r = x - x_u$
我们知道如何根据流动性和价格计算虚拟储备金。请记住,x=L/√p。因此,通过替换,我们得到
$x_r = x - x_u = L/\sqrt{p} - L/\sqrt{p_u}$
由于 p 小于或等于 pu,因此 xr 将始终为正或零。正如预期的那样,当 p 达到上刻度 pu 时,X 的实际储备金变为零。
当当前价格不在区间内时计算 xr
让我们考虑 p 不在区间内的情况。
当前价格低于下刻度
如果当前价格低于下刻度,则该区间的实际储备金是下刻度 pl 和上刻度 pu 的虚拟储备金之差,如下图所示。 原因是我们可以假设 p 最终会达到 pl,并且从 p 到 pl 的交换不会干扰该区间——我们只需要考虑从 pl 到 pu 的交换。
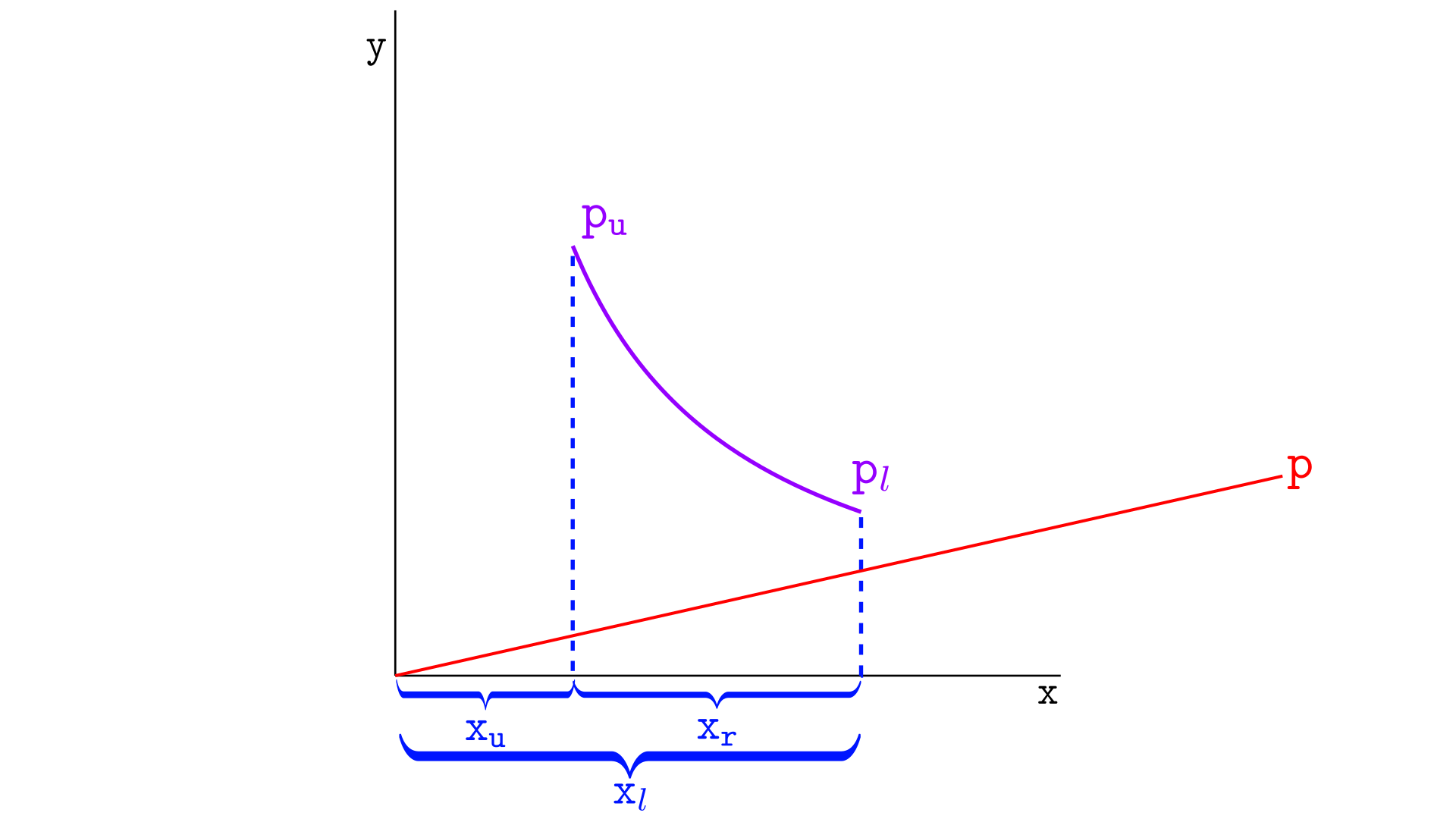
通过替换 $x = L/\sqrt{p}$,我们得到实际储备金为:
$x_r = x_l - x_u = L/\sqrt{p_l} - L/\sqrt{p_u}$
当前价格高于上刻度
如果当前价格高于上刻度,则该区间没有 X 代币的储备金,因此实际储备金 xr 为零。
如你所见,X 代币的实际储备金不仅取决于当前价格和流动性,还取决于上刻度和下刻度。
推导 Y 代币实际储备金的公式
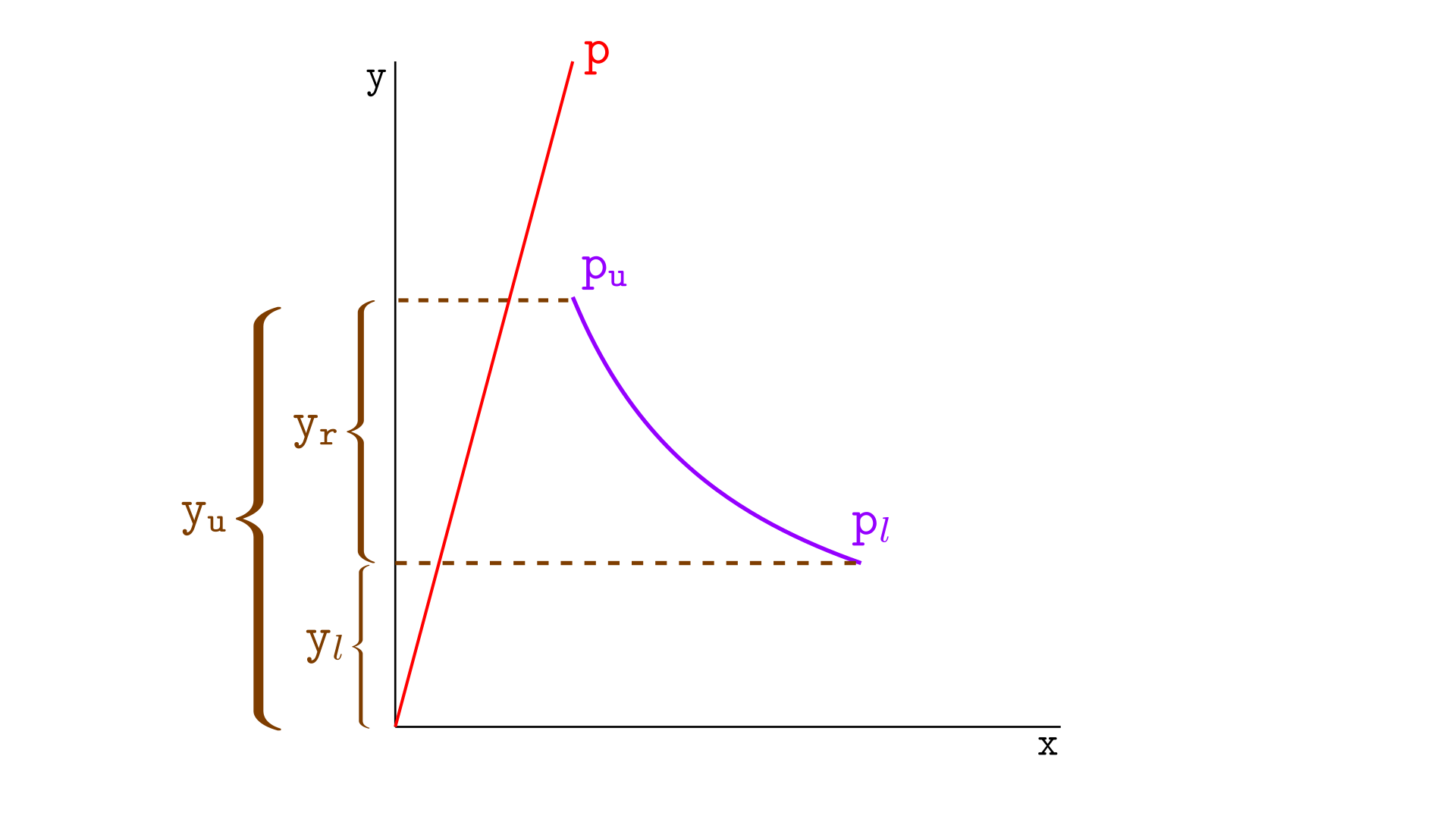
要计算一个区间中 Y 代币的实际储备金,我们将遵循与计算 X 代币相同的策略。 让我们考虑下图。 当价格为 p 时,该区间中有 yr 个 Y 代币——Y 的实际储备金——如左侧所示,虚拟储备金用 y 表示。
将价格移动到下刻度 pl 的交换将从该区间中移除所有 Y 代币。 因此,要计算 yr,我们只需要计算在 p 和 pl 之间的交换中离开该区间的 Y 代币数量。
交换会将虚拟储备金从 y 更改为 yl,因此在这种情况下,实际储备金的计算公式为 y−yl。 记住,Y 代币的虚拟储备金由 $y = L\sqrt{p}$ 给出,我们得到
$y_r = y - y_l = L\sqrt{p} – L\sqrt{p_l}$
由于 p 大于或等于 pl,yr 将始终为正或零。 正如预期的那样,当 p 达到下刻度 pl 时,Y 的实际储备金变为零。
当当前价格不在区间内时计算 yr
让我们考虑 p 不在区间内的两种情况。
当前价格高于上刻度
如果价格高于上刻度,则由 yr 给出的 Y 代币的实际储备金如下图所示,其中 yu 是上刻度的 Y 的虚拟储备金,yl 是下刻度的 Y 的虚拟储备金。
要计算 yr,我们需要考虑从上刻度 pu 到下刻度 pl 的交换,这将使虚拟储备金从 yu 变为 yl。
因此,Y 代币的实际储备金由下式给出:
$y_r = y_u - y_l = L\sqrt{p_u} – L\sqrt{p_l}$
当前价格低于下刻度
如果价格低于下刻度,则 Y 代币中将没有实际储备金,因此 yr 将为零。
计算两个任意价格之间的实际储备金
给定一个区间内的两个任意价格,我们总是可以计算它们之间的实际储备金——换句话说,移动价格从一个到下一个需要交换的代币数量。 推理与上面我们计算一个区间的实际储备金相同,但我们不限制自己使用该区间的末端作为交易的停止点。
两个价格之间的实际储备金也取决于当前价格是否大于或等于最高价格、小于或等于最低价格,或者介于两者之间。
考虑计算价格 pa 和 pb 之间的实际储备金,其中 pb>pa,当前价格为 p,这些价格之间的流动性由 L 给出。我们需要考虑的三种情况如下图所示。
- 当前价格低于下刻度
- 当前价格高于上刻度
- 当前价格介于上刻度和下刻度之间
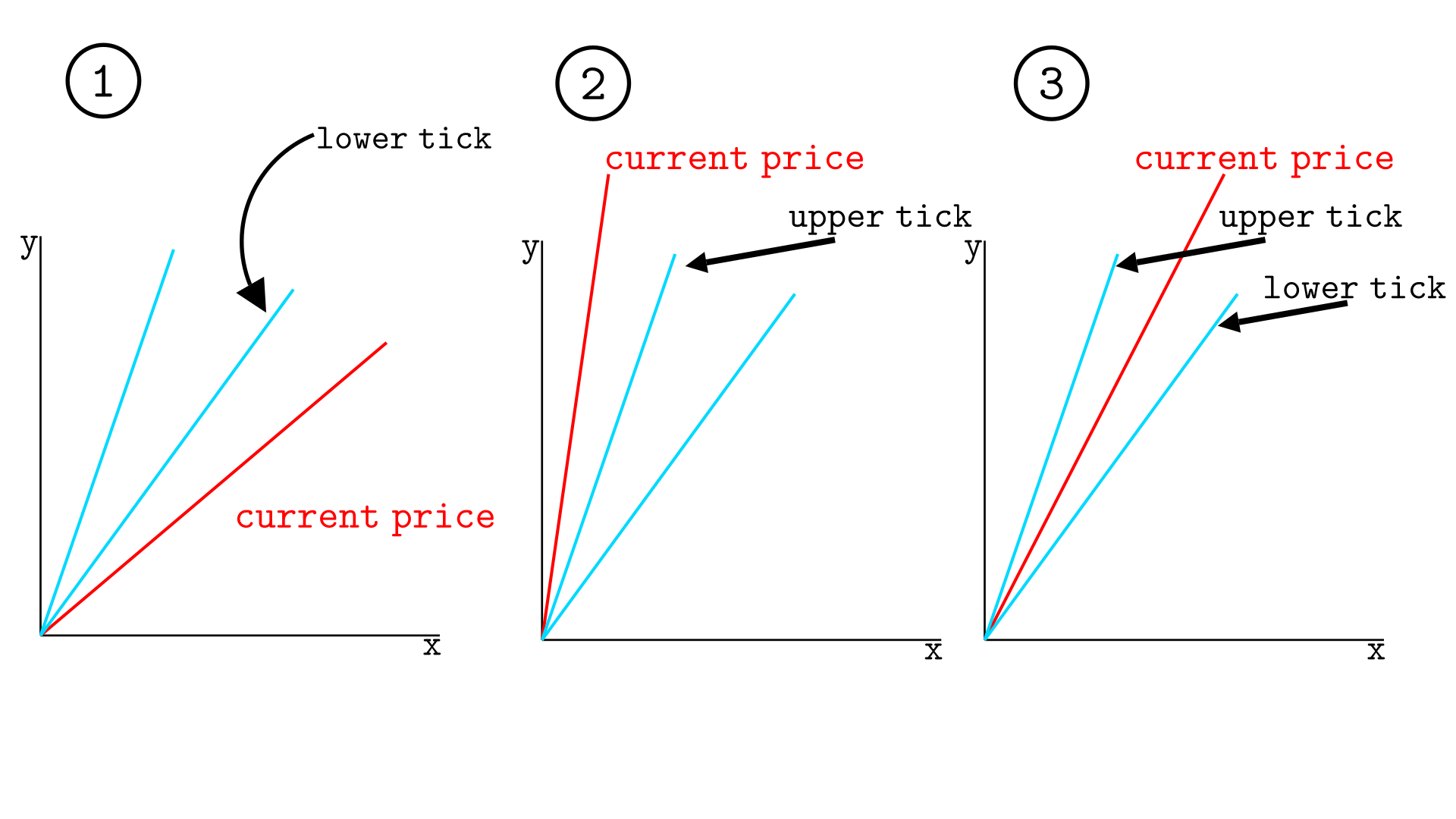
公式如下:
1. 当前价格低于下刻度
在这种情况下,该区间的全部实际储备金都在 X 代币中。
$x_r = L/\sqrt{p_a} - L/\sqrt{p_b}$ $y_r = 0$
2. 当前价格高于上刻度
在这种情况下,该区间的全部实际储备金都在 Y 代币中。
$x_r = 0$ $y_r = L\sqrt{p_b} – L\sqrt{p_a}$
3. 当前价格介于上刻度和下刻度之间
在这种情况下,该区间同时具有 X 和 Y 代币。
$x_r = L/\sqrt{p} - L/\sqrt{p_b}$ $y_r = L\sqrt{p} – L\sqrt{p_a}$
该协议使用这些公式来计算两个价格之间存在的 X 或 Y 代币的数量,给定流动性 L。
在交换中使用上述公式
在 Uniswap v2 中,协议无需担心交换后的最终价格——最终价格没有限制,因为流动性是恒定的,并且价格曲线是无限的。
在 Uniswap v3 中,区间是有限的,因此有边界。 当交换发生在一个区间内时,协议必须计算该区间有多少实际储备金,以确定用户想要交易的数量是否可以完全在该区间内获得,还是只能部分获得。 它通过计算当前价格和区间边界之间的代币数量来做到这一点——如果用户购买 X 代币,则为上刻度;如果用户出售 X 代币,则为下刻度。
在后面的章节中,我们将详细研究 Uniswap v3 中交换的工作原理。
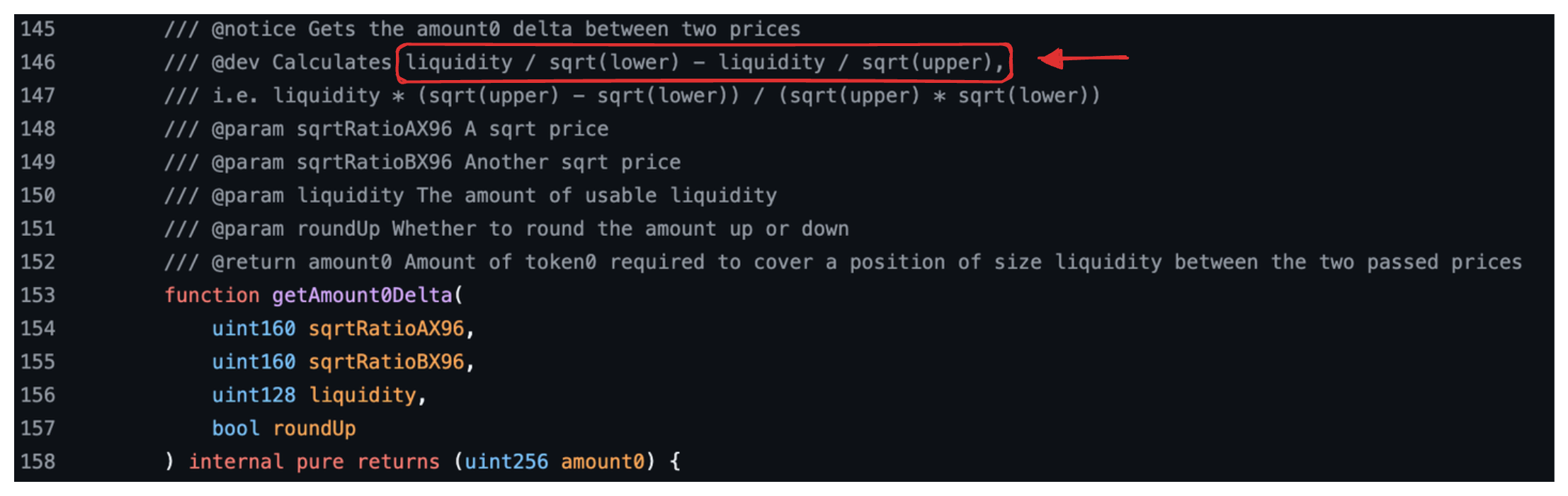
我们上面推导的公式可以在 SqrtPriceMath.sol 库中找到。 这些可以在函数 getAmount0Delta 和 getAmount1Delta 中找到,其签名如下所示以及它们的 NatSpec 注释。
getAmount0Delta
此函数计算并返回两个价格之间的 X 代币数量:较低价格和较高价格。 文本中的红色框显示了我们上面推导的 X 代币实际储备金的公式,$L/\sqrt{p_l} - L/\sqrt{p_u}$。
该函数采用较低价格(sqrtRatioAX96)、较高价格(sqrtRatioBX96)、区间的流动性以及一个指示数量是否应向上舍入的标志。
getAmount1Delta
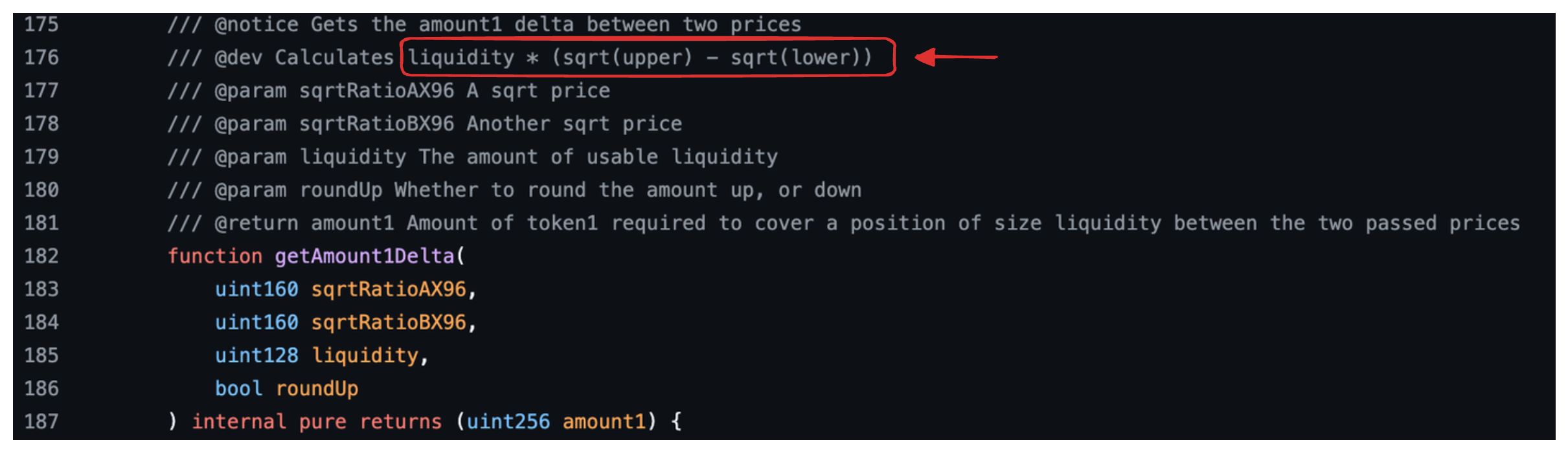
此函数计算并返回两个价格之间的 Y 代币数量:较低价格和较高价格。 同样,文本中的红色框显示了我们上面推导的公式,现在用于 Y 代币的实际储备金,$L\sqrt{p_u}-L\sqrt{p_l}$。
总结
- 一个区间的实际储备金不仅取决于流动性和当前价格,还取决于上刻度和下刻度。
- 给定两个价格 pa 和 pb,对于 pb>pa,这两个价格之间的 X 代币的实际储备金由 $x_r = L/\sqrt{p_a} - L/\sqrt{p_b}$ 给出,在一个流动性为 L 的区间内,并且如果当前价格小于或等于 pa。
- 给定两个价格 pa 和 pb,对于 pb>pa,这两个价格之间的 Y 代币的实际储备金由 $y_r = L\sqrt{p_b} – L\sqrt{p_a}$ 给出,在一个流动性为 L 的区间内,并且如果当前价格大于或等于 pb。
练习
- 假设当前价格为刻度零,并且有一个区间,其流动性 L=1,000,000,000 定义在刻度 -10 和 10 之间。 此区间的 X 和 Y 代币的实际储备金是多少?
- 与问题 (1) 相同,但现在当前价格高于刻度 10。
- 与问题 (1) 相同,但现在当前价格低于刻度 -10。
reCAPTCHA
Recaptcha requires verification.
protected by reCAPTCHA
- 原文链接: rareskills.io/post/unisw...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
